LFCM炉内流动特性的数值分析

周家驹，KIKURA Hiroshige

（1.中国核能电力股份有限公司，北京 100097；2.东京工业大学，日本）

焦耳加热陶瓷熔炉（JCM）是一种将高放废物进行玻璃固化的工艺设备。JCM法的工作原理是焦耳加热效应（当电流通过导体时，在导体表面产生的放热现象），并利用玻璃在高温下是电的良导体这一效应。浸没在玻璃中的两个电极间接通交流电后，玻璃会因焦耳热效应而发热，耗散的电阻热使玻璃保持熔融状态并熔化新的进料。不同于两步法，JCM法具有使用寿命长、一次性处理高放废物多的特点。目前，美国、德国、日本等国家对JCM 技术展开了研究。德国在Pamela 建立了JCM 法的实验设施，并在1985 年进行了运行试验［1］。日本则在东海村建设了液态进料陶瓷熔炉（LFCM），用于对JCM 法的验证［2］。LFCM 的设计如图1 所示，上部呈简单立方体结构，下部为倒金字塔型结构，在立方体结构两侧设有主电极，在LFCM的底端设有副电极。电极通过风冷进行保护，炉内的工作流体主要为高放废物与熔融玻璃的混合物。LFCM 的运行可简单分为4 步，第一步:将高放废料与玻璃投入炉中，仅在主电极之间通电，高放废料与玻璃被加热混合；第二步:当炉内温度达到一定温度时，在副电极之间开始相互通电对炉底进行加热；第三步:当底部被加热至熔融状态时，将工作流体从炉中导入储存容器；第四步:排出一定量的工作流体后，关闭副电极，炉底温度逐渐降低，完成一次循环。运行期间，炉内会析出铂系金属及钼酸盐等产物。这些产物会影响生产，因此，运行时需要监测炉内工况。

图1 LFCM炉设计简图Fig.1 Design preliminary of LFCM furnace

由于JCM 法在大约1 150℃的高温及高辐射环境下运行，且熔融玻璃为不透明液体，所以，现有的监测设备无法对JCM 的运行工况进行较精准的测量。LFCM炉仅在炉顶和主电极附近设置了温度传感器，对炉内温度进行监控。目前，对炉内运行状态的研究主要通过数值仿真进行。2008 年以来，Matsuno、Iso［3,4］等人曾使用商业仿真软件Fluent 对LFCM 炉内的流动状态进行计算，但是模型仅考虑了电场对炉内工况的影响，忽略了磁场的影响。另外，在过去的数值计算中，电场与温度场及流场之间为弱耦合，温度场及流场对电场的影响未能全部模拟。考虑到炉内的工作流体为磁流体，对LFCM炉内的运行工况的预测需要考虑磁场带来的影响。Tanahashi开发的Generalized Simplified Marker and Cell-Finite Element Method（GSMAC-FEM）法［5］能够在自然循环模型中对流场、温度场及电磁场进行强耦合，因此，相较于过去的商用软件，能够对LFCM炉内的流动进行更为准确的模拟。Duong 等人使用GSMAC 法对电场与磁场进行了耦合，并将LFCM 炉简化为一个简单方腔，计算了其中的流体流动情况［6］。然而Duong的模型由于过度简化，并无法真正预测LFCM炉内的流动工况，本文通过建立接近于LFCM炉的物理模型，使用GSMAC 法计算了LFCM 炉在第一步时的运行工况。

1 LFCM的物理模型建立

1.1 影响LCFM炉内玻璃流动的因素分析

在LFCM炉内，流场、温度场以及电磁场之间相互作用，因此，本文在进行建模时需要考虑动能耗散、洛伦兹力、浮力、热导率、摩擦、焦耳效应以及电动势对炉内运行工况带来的影响。以上变量在LFCM炉的物理模型中用以下关系式表示。

关于流场，连续性方程为:

式中，v——速度，m/s；

∇——Nabla算子。

纳威斯托克斯方程为:

式中，ρ——密度，kg/m3；

t——时间，s；

p——压强，Pa；

μ——黏度系数，Pa·s；

D——变形速度张量，s-1；

Tem——电磁应力张量，s-1；

β——热膨胀系数，K-1；

T0——标准温度，K；

T——温度，K;

g——重力加速度m/s2。

关于温度场以及电磁场，热能方程为:

式中，Cv——比热，J/(kg·K)；

q——热通量，W/m2；

JC——感应电流密度，A/m2；

σe——电导率，S/m。

安培麦克斯韦方程:

式中，μm——磁导率，H/m；

A——磁向量势，T·m；

Φ——电势，V；

Jf——线圈电流密度，A/m2。

根据电荷守恒可得:

另外，本文在建模过程中也对LFCM炉内流动模型做了如下简化:

（1）流体为牛顿流体；

（2）浮力项可用布西涅斯克近似表示；

（3）流动为层流且不可压缩；

（4）忽略位移电流。

1.2 LFCM模型

本次所使用的模型如图2 所示。考虑到LFCM炉在第一步运行时仅有一对主电极工作，底部副电极处于关闭状态，因此，模型对倒金字塔结构进行了简化，仅保留了主电极下的一对斜边以降低计算难度。其中，蓝色部分为LFCM炉，电极设置在一对斜边上方；白色部分为LFCM炉外部，用于电磁场的整体分析。流体区域（蓝色部分）的尺寸为630 mm×760 mm×760 mm，使用27 000 个六面体网格分割，顶层表面与电机面设为等温面，温度为1 000˚C，其余表位为绝热面，电极间电势差为95 V，流体初始温度为1 000˚C。电磁场大小为流体区域的3 倍，被分割为48 000 个六面体网格。磁流体区域的外边界满足电磁条件如下:

式中，H——磁场强度，A/m；

n——向外的单位向量。

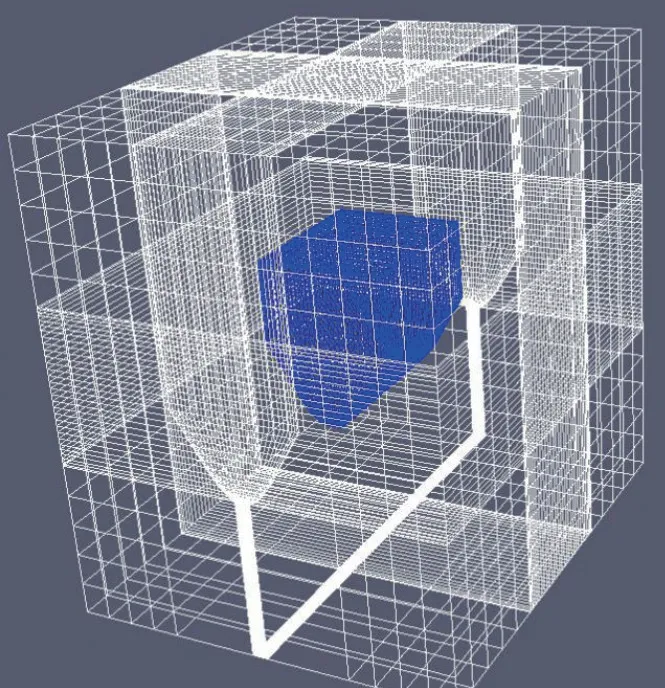
图2 LFCM模型的网格构建简图Fig.2 Grid construction diagram of LFCM model

计算中的工作流体为曾在LFCM运行试验中使用的P0797 玻璃，其物理参数见表1［2］，除体积膨胀系数外，其他参数均为测量值且数值随温度变化。为了降低计算的复杂程度，相对于黏度系数以及电导率变化较小的其他参数在本文中设为常数，工作流体的最终参数见表2。

表1 P0797玻璃物理参数［2］Table 1 Parameters of P0797 glass

表2 模型中所使用工作流体的物理参数Table 1 Physical parameters of the working fluid used in the model

2 仿真结果与分析

在计算中，当电极之间的直流电压恒定时，流体温度因为焦耳效应逐渐升高。由于腔体内与等温层之间具有温度差，所以，腔体内出现对流，腔体内电极间的流动如图3所示。在腔体中心以及靠近电极的部分可以观测到稳定向下的流动，而在腔体的底部几乎观测不到流动，流动速度随着时间逐渐变大。然而，在通电后5 000 s，流动逐渐不再稳定，如图3（d）所示，在腔体顶部能够观察到漩涡存在。该现象的发生可以被认为有以下两个原因:随着温度的升高，工作流体的黏度降低，其阻力也随之减小；由于腔体内温度逐渐升高，流体与等温层之间的温度差逐渐变大，从而导致对流越来越剧烈。以上两点导致腔体内的流动在电极间接通电流后逐渐由稳定变为不稳定。

图3 通电后前5 000 s腔体内流场情况Fig.3 Simulation result of velocity field in the cavity before 5 000 s

长时间通电后，腔体内流动的情况如图4所示，图4（a）～图4（d）分别为通电后7 000～10 000 s 时腔体内的流场图。相对于前5 000 s，腔内的流动速度更大且更加不稳定。腔体中心部分稳定向下的流动已经消失，且漩涡出现的位置在4个不同时间点也各不相同。然而在电极处及其下方斜边附近依旧能够观察到稳定向下的流动，该流动在下降到一定程度后流向腔体中心。出现这部分稳定流动的原因可以认为电极部分是等温层，持续被冷却，导致附近的流体温度始终低于腔体中心，流体受重力影响持续向下流动。长时间通电后，炉内产生的这种不稳定流动能够使高放废液与玻璃之间的融合相对更加均匀，能够满足设计初期通过焦耳热产生的自然对流将高放废物与玻璃混合达到玻璃固化的初衷。但是，流场的不稳定也导致了炉内析出的铂系金属以及钼酸盐难以追踪，需要在运行时增加对副产物的监测。

图4 通电后腔体内流场情况Fig.4 Simulation result of velocity field in the cavity

温度的变化同样显示出了流动由稳定变为不稳定的变化。腔体中通电部分中心点的温度变化如图5所示，温度在通电后的4 000 s内持续上升，但是在大约4 000 s 时出现了明显的下降，之后温度在波动中逐步上升。这是因为在施加电流初期，腔体内与等温层之间温度差较小，因温度差产生的对流相对较小，来自顶端的低温流体在经过中心点时已被加热。然而随着通电时间越来越长，腔体内与顶部等温层之间的温差逐渐增大，流体的流动也愈加剧烈，使一定时间后来自顶部的低温流体在通过中心点时，温度依旧保持较低。因此，通电一定时间后，腔体内温度的变化为波动上升。

图5 腔体中心温度Fig.5 Central temperature of the cavity

这种温度变化在长时间通电后不再稳定的现象通过图6所示的温度场也可观察到，炉内温度分布随时间发生无规律变化。但在靠近电极的区域也可以观测到稳定的低温层，而该低温层的位置也与图4中靠近电极的稳定流动位置基本相同。除了靠近电极部分，腔体的底部也能观察到低温层。由于电极仅设置在腔体上部，底部几乎无电流通过，所以，相对于设有电极的上部，底部焦耳效应很弱，温度上升的原因主要来自上部流体的温度差。同时，由于底部几乎没有温差，所以，相较于腔体上部，其流动也十分微弱。这种在第一步运行时炉底部为低温的结果，可以保持底部熔融玻璃具有较高的黏性以防止炉内析出的铂系金属过多沉淀至炉底。而炉上部在长时间通电后维持在约1 150°C的结果也与设计相符。同时还能看到炉内上部的温度场是不断变化的，但是由于高温高辐射的环境限制，现在的设计中炉内温度的监测点有限。因此，当个别监测点出现温度变化异常时，可能仅是由于低温玻璃流过监测点所造成，并非炉内出现异常需要停机。所以，实际运行时，本文需要对炉内流动进行监测以达到对温度变化的准确评估，从而判断炉的运行状态。

图6 通电后腔体内的温度场Fig.6 Temperature field in the cavity after electrification

图7 为浮力、洛伦兹力和黏性力的体积力工作流体中的变化情况。可以发现，在通电一定时间后，浮力的平均值远大于黏性力和洛伦兹力，因此，可以认为浮力是影响工作流体流动特性的主要因素，电磁场对流动特性的影响较小。但在刚开始通电时，洛伦兹力的大小与浮力相似，洛伦兹力也同样对流动有所影响。因此，我们依旧需要考虑电磁场对LFCM炉内流动行为的影响。

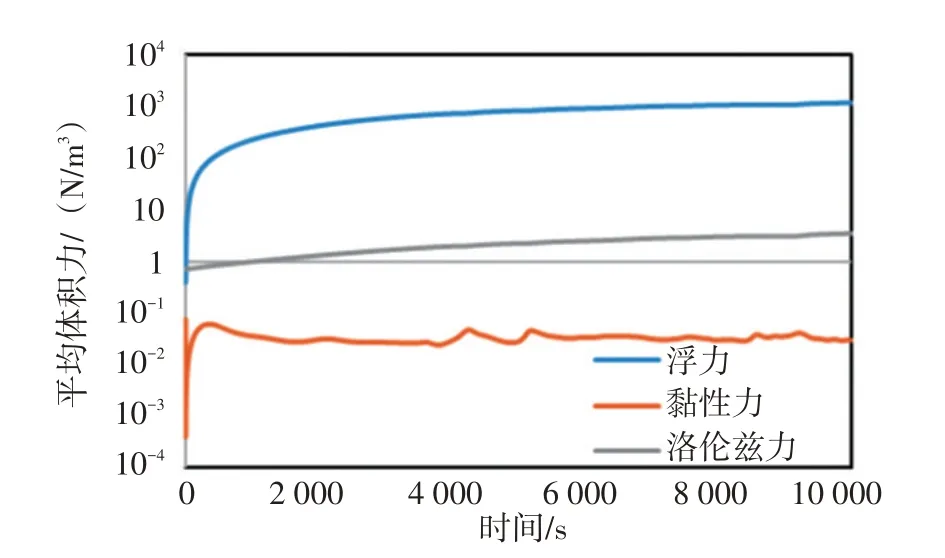
图7 平均体积力的变化Fig.7 Change in average volume force

3 结论

本文通过计算分析了JCM炉中LFCM型炉在执行第一步运行时炉内流体的流动特性并得到了以下结论。这些结论将对未来商业运行JCM炉设计以及运行提供一定的参考依据。

（1）通过计算发现，在LFCM炉的第一步运行时，流体在LFCM 炉底部几乎没有流动，LFCM上部在通电初期有稳定的流动，在通电一定时间后流动逐渐变得不再稳定。

（2）LFCM炉内温度在通电后一定时间内逐步上升，温度在升至一定值后炉内温度场不再稳定，呈波动上升状态。但由于电极始终被冷却、炉底受焦耳效应影响较小，因此，在电极附近和LFCM炉底部存在稳定的低温层。

（3）由于电极附近存在稳定的低温层，而该低温层与LFCM内部存在温度差，因此，在电极附近始终存在稳定向下的流动。

（4）在LFCM 炉的第一步运行中，浮力对流动特性的影响远大于洛伦兹力和黏性力，但在刚开始通电时，洛伦兹力的大小与浮力相似，洛伦兹力也同样对流动有所影响。因此，我们依旧需要考虑电磁场对LFCM 炉内流动行为的影响。

（5）长时间通电后，炉内的流场和温度场都不再稳定，这对LFCM炉的运行具有一定的影响。由于流动不稳定，炉中铂系金属及钼酸盐等副产物的追踪较为复杂；温度场的不稳定则导致无法对运行时得到的温度数据迅速做出准确评估，因此，运行时应考虑设置监测炉内流动的设备，从而使炉中工况能够被精确的评估。