某款配置手动变速箱汽车传动系统扭振模态分析
田文祥 缪国
摘 要:本文主要针对某款配置六挡手动变速箱的汽车,建立了从发动机到车轮整个传动系统的扭振模型,通过自由振动计算分析获得了各挡位工况下传动系统的扭振模态频率及对应阶的振型。进一步对比分析了不同挡位对传动系扭振模态频率的影响;最后对同一挡位的模态特征进行了贡献度分析,为手动挡车辆传动系统扭振调谐提供参考。
关键词:手动变速箱 前置后驱 扭振分析 模态分析 贡献度分析
1 引言
汽车动力传动系统一般由发动机、离合器、变速箱、万向节、传动轴、主减速器、差速器、驱动半轴和车轮等组成,它们之间通过各种形式的连接构成了力学特性较为复杂的傳动链;在整个传动链中有转动惯量相关较大的部位,也有扭转刚度相对较大的部位,在实际使用过程中这些部位会发生动势能的相互转换,形成了一个扭转振动系统,在激励的作用下系统会产生扭转振动。当激励频率与系统的固有频率接近时,系统会出现强烈的扭转共振,相关部件所受载荷将急剧增加。若这种情况发生在车辆经常使用的范围内,将对动力传动系统零件的使用寿命有严重影响。情况严重时,传动系统中甚至还会出现负转矩,使啮合的轮齿间发生撞击,并产生强烈的噪声,增加对车内及车上环境的噪声污染[1]。在传动系匹配设计的时候,通过合理调整动力传动系统扭振模态频率分布[2-5],使其避开发动机常用转速对应的激励频率及避开悬置系统的关键模态频率,有利用降低由传动系统扭振导致的车内异响,提高整车声品质[6]。
本文以一款配置手动变速箱的前置后驱动力传动系车型为例,建立了从发动机到车轮整个传动系的详细的扭振模型,通过自由振动计算分析获得了各挡位工况下传动系统的扭振模态频率及对应阶的振型。进一步对比分析了不同挡位对传动系扭振模态频率的影响;然后对同一挡位的模态特征进行了贡献度分析,从机理端找出对特定阶模态频率影响最大的惯量单元和刚度单元,为汽车动力传动系统扭振调谐提供指导。
2 动力传动系统建模
动力传动系首端为发动机,末端为车轮及与之相连的车身平动质量,组成了一个多质量的弹性扭转振动系统。在计算系统的固有频率和振型时,忽略系统的阻尼,即分析系统的无阻尼自由振动特性,给出无阻尼自振频率和相应阶的振型。
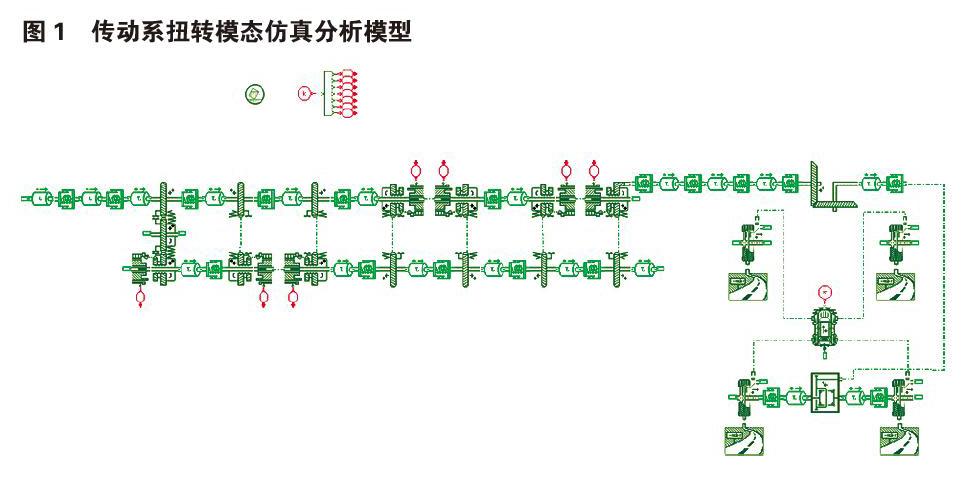
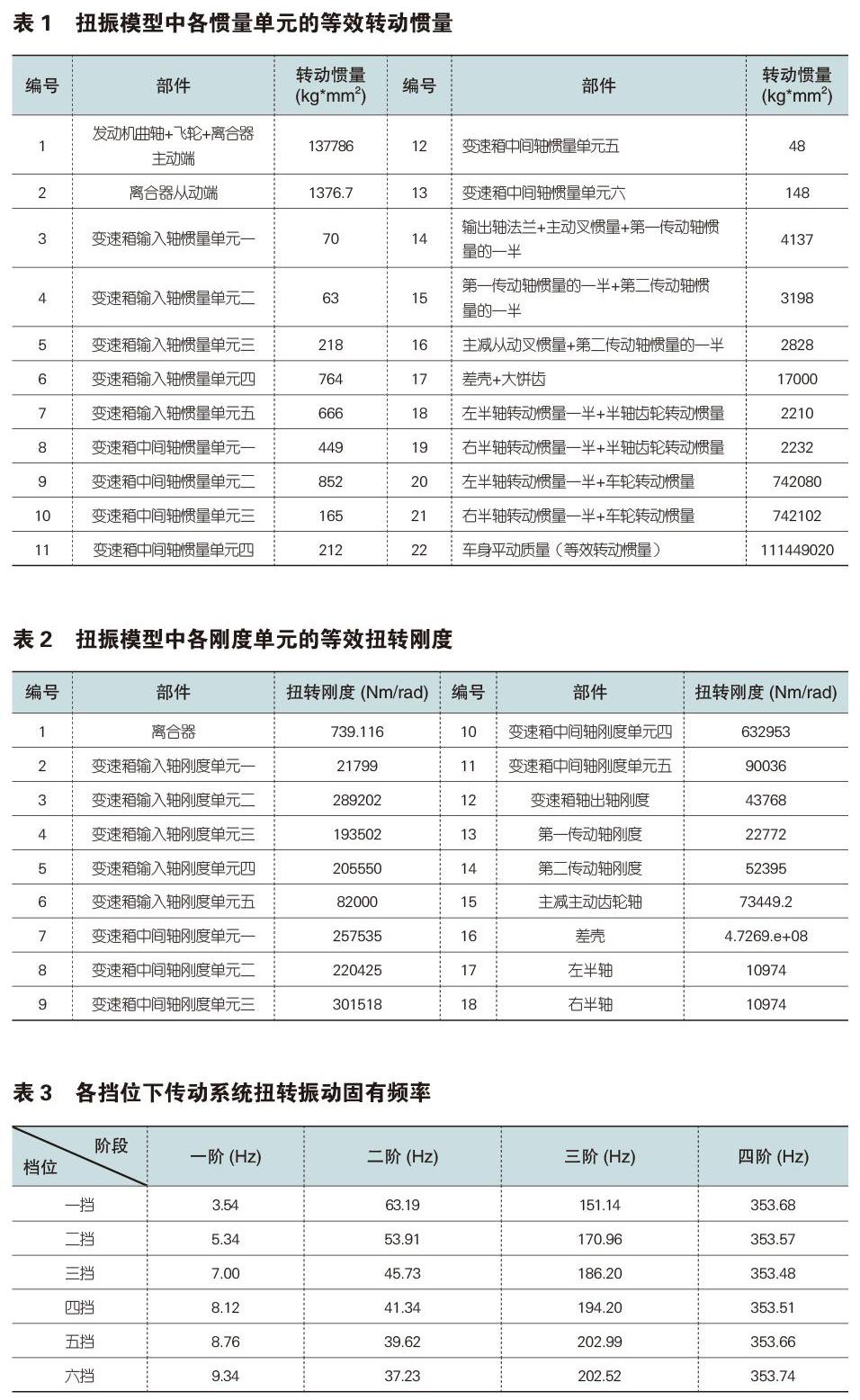
图1为根据振动力学理论和扭振分析当量简化原则,使用Amesim软件建立的上文提到的一款配置手动变速箱的前置后驱动力传动系汽车的扭振模态分析模型。如图1中所示,区别与以往扭振分析工作中将变速箱简单的简化为一个惯量单元和刚度单元,为了充分了解变速箱内部的扭转振动特性,文中对变速箱部分进行了较详细的当量简化建模。模型中有22个惯量单元和18个刚度单元,模型惯量参数如表1所示,模型刚度参数如表2所示。
3 传动系统扭振模态计算及分析
通过自由振动分析,得到各挡位工况传动系统的扭转振动固有频率如表3所示。
由固有频率表3分析可知,第一阶模态频率分布在3Hz~10Hz,频率随挡位升高而增大。第二阶模态频率分布在64Hz~37Hz,频率随挡位升高而减小,对应的工作转速在发动机常用转速范围内。第三阶模态频率分析布在151Hz~203Hz,频率随挡位的升高而增大。第四阶模态频率稳定在353Hz左右。
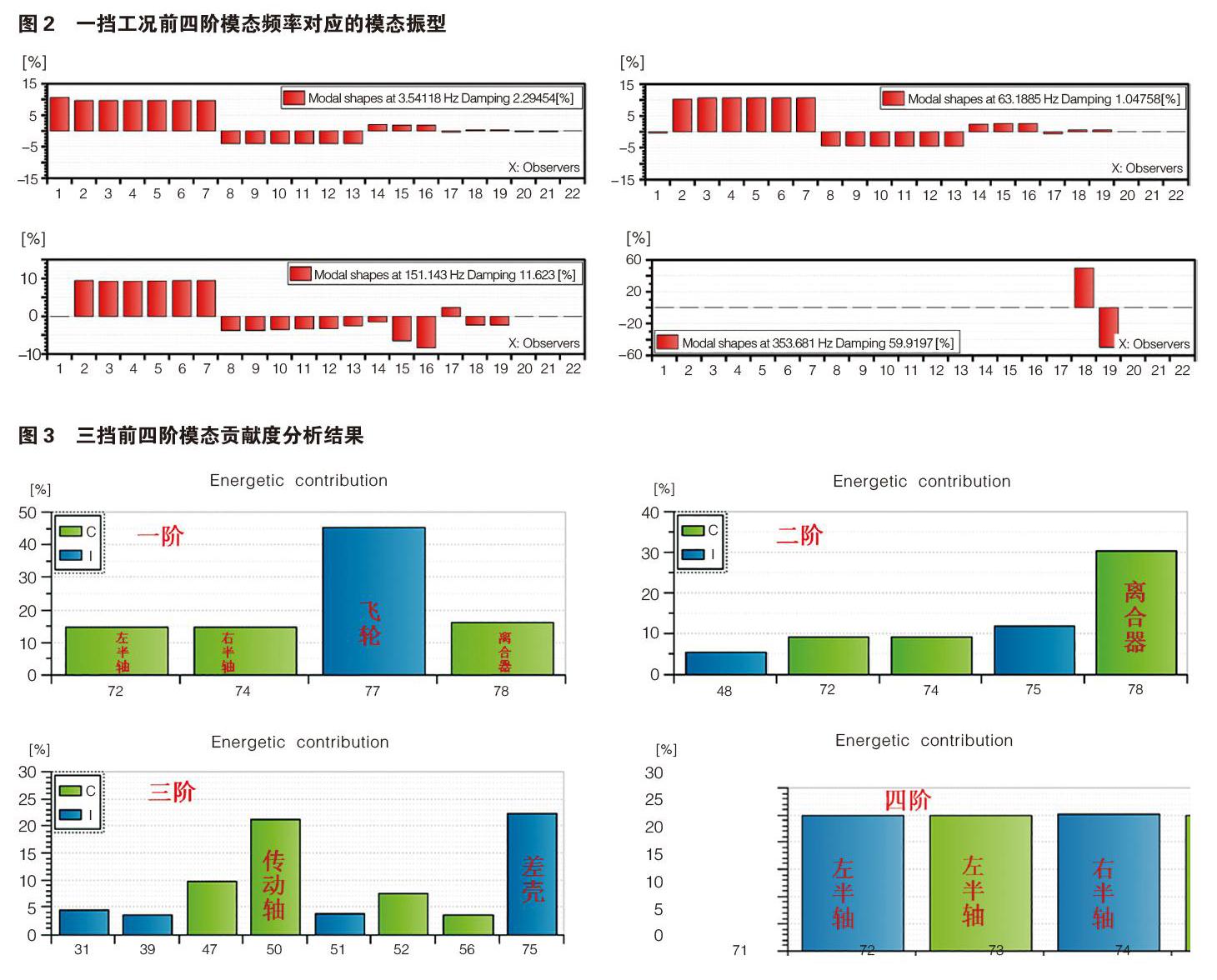
图2给出了一挡工况前四阶模态频率对应的模态振型的分析结果,篇幅原因其它挡位的振型分析结果不便给出。
由振型图分析可知,第一阶为系统模态,振型中幅值较大的部位在飞轮、输入轴。第二阶也为系统模态,振型中幅值较大的部位在输入轴、中间轴,且由上面的频率分析结果可知,该阶模态对应的工作转速在发动机常用转速范围内,该阶模态易被激起,可能会导致变速箱敲击异响。第三阶同样为系统模态,振型与第二阶相似,在传动轴段有稍许变化。第四阶为半轴局部模态。
4 传动系统扭振模态频率贡献度分析
通过空间变换处理,可以得到各挡位前四阶扭振模态贡献度分析结果,篇幅原因下面只给出了三挡前四阶模态贡献度分析结果如图3所示,其中I表示惯量单元,C表示刚度单元。
由分析可知,第一阶系统模态的频率主要受飞轮惯量、离合器刚度、半轴刚度的影响,且随着挡位升高离合器刚度的影响占比增大,半轴刚度的影响占比减小。第二阶系统模态的频率主要受离合器刚度、半轴刚度、差壳转动惯量的影响,随着挡位的升高半轴刚度、差壳转动惯量的影响占比增大。第三阶系统模态的频率主要受传动轴刚度和差壳转动惯量的影响,它们的影响占比随挡位的变化不大。第四阶半轴局部模态的频率主要受半轴刚度和半轴转动惯量的影响,它们的影响占比随挡位的变化不大。
5 结语
本文以一款配置手动变速箱的前置后驱动力传动系车型为例,建立了从发动机到车轮整个传动系的详细的扭振模型,通过自由振动计算分析获得了各挡位工况下传动系统的扭振模态频率及对应阶的振型。结论如下:
1)对比分析了不同挡位对传动系扭振模态频率的影响,分析发现,第一阶模态频率随挡位升高而增大。第二阶模态频率随挡位升高而减小。第三阶模态频率随挡位的升高而增大。第四阶模态频率较稳定,不随挡位的变化而变化。
2)通过对系统模态振型的分析发现,第一阶为系统模态,振型中幅值较大的部位在飞轮、输入轴。第二阶也为系统模态,振型中幅值较大的部位在输入轴、中间轴,且由上面的频率分析结果可知,该阶模态对应的工作转速在发动机常用转速范围内,该阶模态易被激起,可能会导致Rattle。第三阶同样为系统模态,振型与第二阶相似,在传动轴段有稍许变化。第四阶为半轴局部模态。
3)然后对同一挡位的模态特征进行了贡献度分析,从机理端找出对特定阶模态频率影响最大的惯量单元和刚度单元,为汽车动力传动系统扭振调谐提供指导。
参考文献:
[1]喻凡 and 林逸,汽车系统动力学. 2005:机械工业出版社.
[2]康强,et al.,某前置后驱乘用车传动系扭振模态理论计算及试验测试. 汽车技术,2015(01):p.40-43.
[3]毕金亮,et al.,动力传动系统扭转模态及灵敏度分析.振动工程学报,2010.23(06):p.676-680.
[4]陈宏强,汽车动力传动系扭振分析与仿真优化.2012,湖南大学.
[5]蔡辉,后驱汽车传动系统设计与扭振分析. 2015,南京航空航天大学.
[6]HaraldNaunheimer,瑙海姆,宋进桂,et al. 汽车变速器理论基础、选择、设计与应用[M]. 机械工业出版社,2014.

