两栖球形机器人的路径规划策略
马宇科,郑 亮,2*,胡高凯,吉晓雯,司兆怡,刘晏彤
(1.吉林农业科技学院,吉林 吉林 132101;2.长春理工大学,吉林 长春 130022)
1 引 言
目前,在机器人研究领域,两栖仿生机器人的研究逐步成为研究热点,通过对一种动物运动方式的长时间观察与研究,提出了相应具有运动模式的仿生机器人的设计方案。这类机器人具有较为灵活的两栖运动能力,能够在水下实现最佳的路径控制和对目标具有一定的识别与追踪能力,但是,以往提出的仿生机器人大多只适应于水下的运动环境,对于目前所需要的两栖运动环境并不合适,球形两栖机器人能够很好地解决这一问题。在一些特殊的应用环境下,例如两栖侦察、海底探测、深海探测等相关领域,一般性能的机器人无法满足要求,所以两栖机器人应运而生。由于两栖机器人特殊的灵活性、超强的适应能力、便于投放和回收的优越特性,使它可以独立在水下完成侦查、搜救、探测、数据收集等工作。所以两栖球形机器人很自然地成为人类延伸自己感知能力的主要工具之一。本文提出的两栖球形机器人是一种先进的执行装置,包括运动推进器,传感器,控制板和安装在球形壳体中的电源装置。作为微型球形机器人,这种机器人得到广泛应用主要依靠四个技术优势。第一个特点是球形机器人是一种可移动行走的移动机器人,可以保持先进的平衡性、稳定性和运动连续性。第二个特点是球形机器人具有良好的密封性,可以完全保护内部控制单元和机构,这是其他机器人无法做到的。第三个特点是球形机器人具有很强的适应性,能在无人区、灰尘、湿气、腐蚀性和恶劣环境下完成任务。最后是矢量推进器具有更高的稳定性和灵活性,能使机器人保持更好的水下运动性能和抗噪声干扰能力。
两栖机器人控制技术发展迅速,北京理工大学仿生机器人与系统教育部重点实验室郭书祥团队研究的两栖球形机器人,是以球形为主体的机器人,整体结构分为上半球和下半球。在陆地模式时,下半球可以折叠到上半球,用4个由8个舵机组成的机械臂行走,在水下模式的时候,折叠的上半球通过二个舵机封闭下半球,由喷水电机推进行走,球体内部也安装了通信和稳定控制模块,该球基本实现了球形机器人的基本功能,但没有实现水下的自动路径规划[1-3]。北京邮电大学孙汉旭团队研究的球形机器人以摩擦力为驱动力,没有被动摩擦力的球形机器人,该机器人具有运动效率高,对路面要求低,适应能力强等优点[4]。哈尔滨工程大学叶秀芬团队,也对球形机器人“基于喷水推进的微小球形水下潜器”进行了深入的研究[5]。天津理工大学郭健团队也对球形机器人在陆地上的路径规划进行了深入的研究[6]。但目前针对水下路径规划的相关研究相对较少。
机器人执行有障碍的复杂水下任务时,路径规划对水下机器人实现任务目标具有非常重要的意义。文献[7]提出了一种基于先验知识强化学习策略的最佳路径选择的新算法。针对未知空间中移动机器人的路径规划问题,Yuan等提出了一种基于门控递归单元-递归神经网络模型的动态路径规划方法[8]。Bae等提出了一种结合深度学习和卷积神经网络的多机器人路径规划算法[9]。文献[10]提出了一种非完整的三轮移动机器人的路径规划和控制方法,该机器人用于在道路跟踪和复杂环境中进行在线导航。文献[11]开发了一种“增强轮辋跳跃”的方法,该方法不依赖于逐点定位,而是通过找到障碍物之间的多次切线来获得最短路径。尽管在两栖球形机器人的路径规划方面已有许多研究,但是多数研究是基于单一的陆地环境下进行的。本文以实现球形两栖机器人最佳路径规划为研究目标,针对两种基于视觉伺服的广义约束优化(Generalized Constraint Optimization,GCOP)和序列二次规划(Sequential Quadratic Procontrol,SQP)的机器人运动控制算法进行对比分析,使用视觉伺服传感器实现两栖机器人的最佳路径规划,并实时对监测动态目标进行标定、移动目标监测、水下障碍物识别和目标跟踪。最后,通过水下运动测试和仿真来对比验证算法的可行性。该运动的路径规划方案提高了球形两栖机器人的运动性能,使机器人可以执行更为复杂的水下任务。
2 两栖球形机器人设计
2.1 机械设计
新型两栖球形机器人不仅具有良好的陆地运动能力,而且能够实现水下多自由度的运动。图1是机器人陆地运动模式和水下运动模式的结构。在陆地模式下,机器人下半球壳体通过两个舵机折叠至上半球,4个喷水推进器根据相应步态调整实现陆地行走[12]。在水下模式下,下半球闭合,机器人可以利用4个水下推进器实现水下多自由度运动。相比其他两栖球形机器人,加入了稳定控制块、4个激光测距模块和4个视觉采集模块,用来实现路径规划的相关参数采集。

图1 两栖球形机器人的机械结构Fig.1 Mechanism of amphibious spherical robot
2.2 硬件构成
两栖球形机器人采用模块化设计,通过各模块的合理分布与协调工作,保证球体运动的可靠性和稳定性。如图2所示,球体主要搭载一块嵌入式处理器(ARM S3C6410,2 GB DDR3,linux 3.12.0),用于数据处理;GPS模块和声纳模块用于机器人通讯。陀螺仪传感器对机器人进行姿态感应与调整,伺服电机和电机控制器控制机器人的运动和姿态,图像采集模块用于机器人的视觉识别与动态目标捕捉,5000 mA锂电供电模块用于机器人的供电。
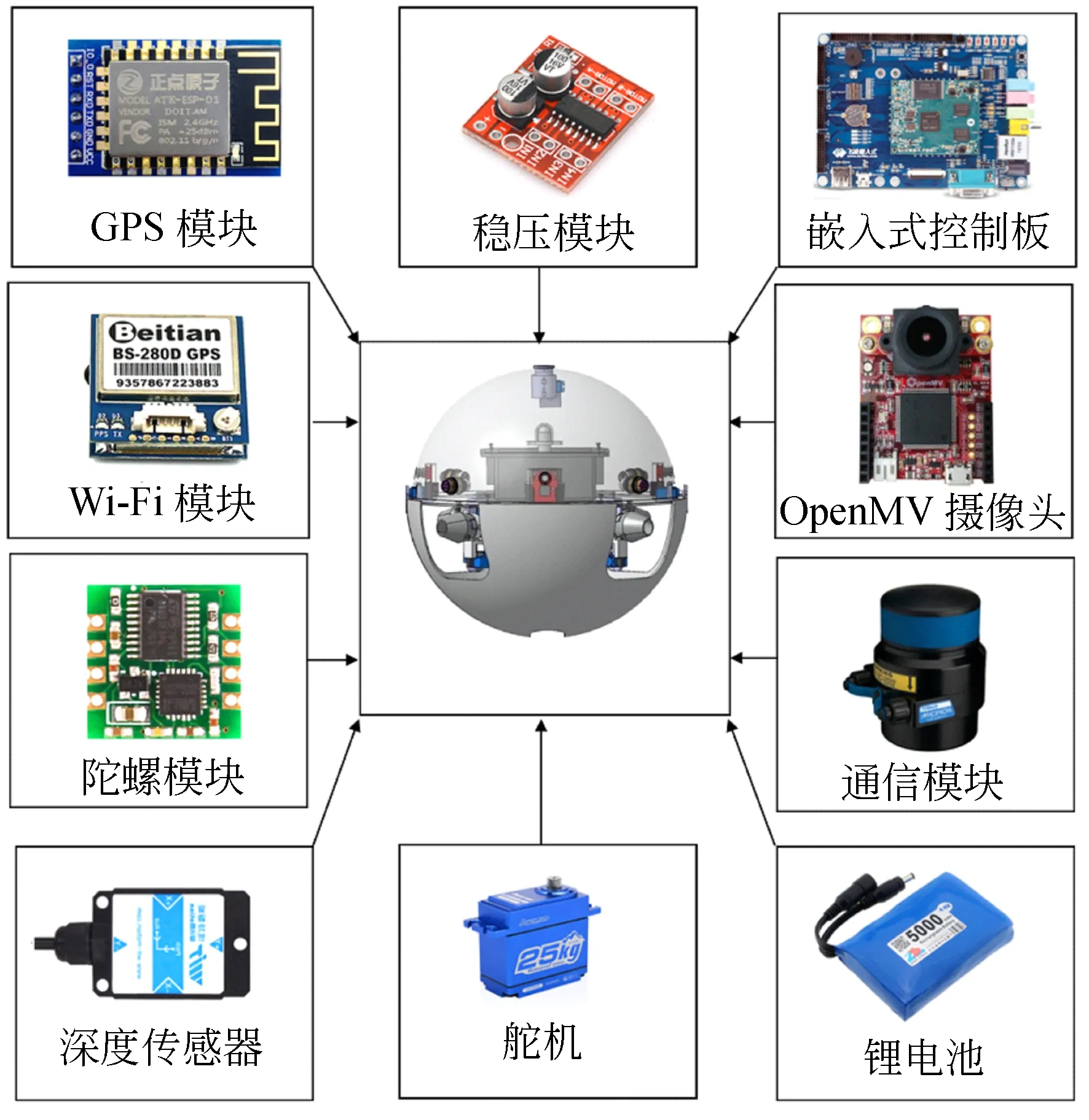
图2 两栖球形机器人的硬件结构Fig.2 Hardware structure of amphibious spherical robot
3 两栖球形机器人上浮下潜原理

图3 机器人上浮和下潜原理Fig.3 Principle for robot floating and diving
球体分为上半球和下半球两个仓室,如图3所示,下仓室装有排水口,通过上仓室的仓室气泵将上仓室的空气压入下仓室,通过下仓室的水压调节罐控制水箱的进水量,根据阿基米德浮力原理,球体的浮力由球体排开水的体积决定。当机器人下潜时,防水舵机顺时针旋转,将放气的阀门关闭,水从球体一端的孔进入,由于压力的作用,原本在球体内部的气体从球的另一端排出。水的重量再加上球体本身防水舵机的重量使球形机器人进行下潜。上浮时,防水舵机逆时针旋转,将二氧化碳气瓶中的压缩二氧化碳气体放出,此时排气孔和进水孔都变成了排水孔,机器人上浮。
4 运动控制和路径规划算法
4.1 非线性6自由度算法
两栖球形机器人能够在陆地与水下多自由度运动,在陆地上要具有4个自由度,在水下要具有6个自由度的运动模式。
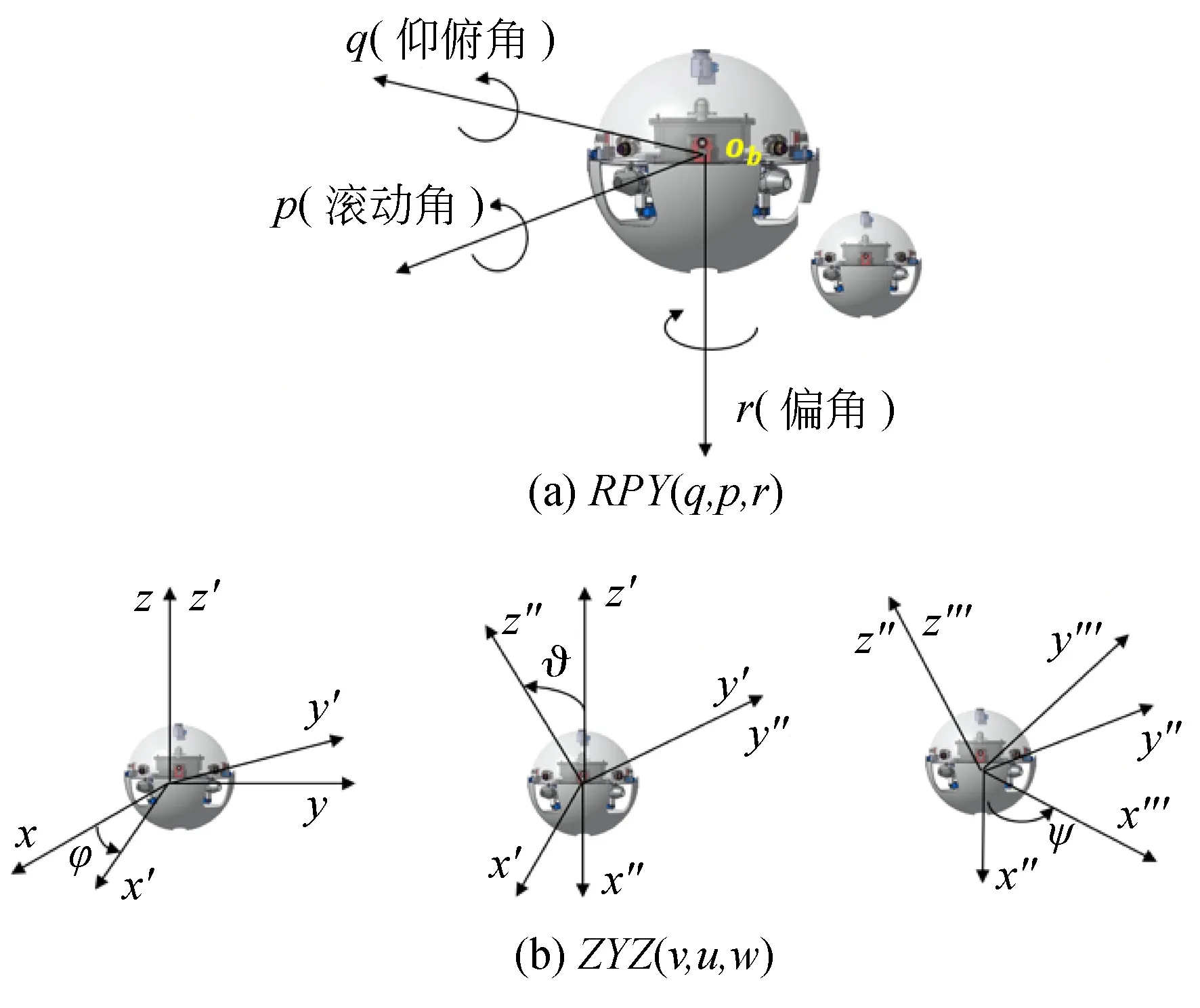
图4 6自由度建模坐标标定Fig.4 Calibration of 6-DOF modeling coordinate
6自由度包括RPY(q,p,r)和ZYZ(v,u,w)参考系。为了达到精确控制的目的,分别给出了两种受控源的旋转矩阵。如图4所示,参考坐标以x轴围绕的角度“q”旋转,并用矩阵Rx(q)表示。参考坐标以Y轴围绕的角度“p”旋转,并用矩阵Ry(p)表示。参考坐标以Z轴围绕的角度“r”旋转,并用矩阵Rz(r)表示[13]。
R(φ)=Rx(q)Ry(p)Rz(r)=
(1)
假设参考坐标绕Z轴旋转一个φ的角度,并且旋转矩阵为Rz(φ), 参考坐标绕Y轴旋转一个ϑ的角度,并且旋转矩阵为Ry′(ϑ),参考坐标绕Z轴旋转一个ψ的角度,并且旋转矩阵为Rz″(ψ)。最终坐标系的方向是通过合成相对于当前坐标系的旋转矩阵并通过右乘计算得出的,获得基本矩阵为:
R(Φ)=Rz(φ)Ry′(ϑ)Rz″(φ).
(2)
旋转矩阵为:
(3)
参数ϑ在[π,0],可以表示为:
(4)
参数φ在[-π,0],可以表示为:
(5)
4.2 GCOP控制算法
假设物体的表面由m个方程表示为:hi(x),i=1,2,…,m,并且它的内部方程为[14-16]:
h1<0∧h2∧…∧hm<0.
(6)
对每个hi构造新的函数:
(7)
其中:t是一个小的正实数,vi是x和t的函数,对整个物体,构造函数V:
(8)
验证从hi到vi和vi到V的两个变换的性质。首先,函数vi对任意x和t总是正的,其次,vi是关于hi的递增函数,即当hi>0时vi的值和当hi<0时vi的值。如果t≪1,vi可以近似表示为:
(9)
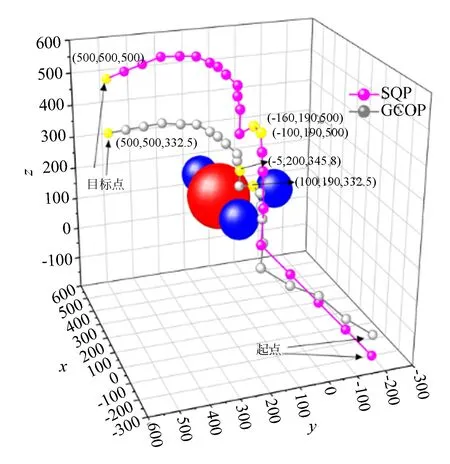
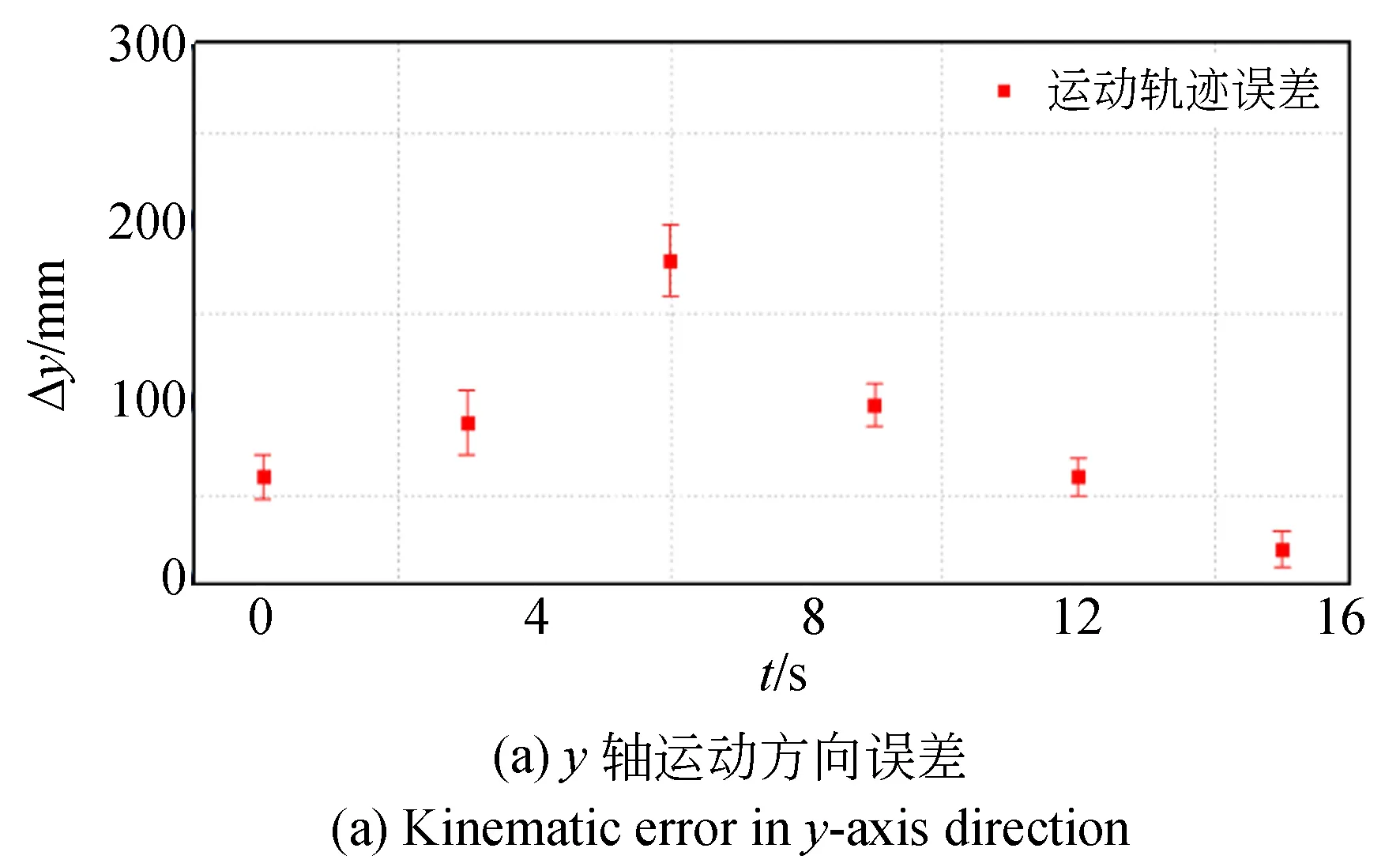
其中:O(t2)为一个值非常小的正数。式(9)表明,除了点在物体表面附近时,hi=0;当hi>0时,vi>t;当hi<0时,vi 对于在物体hi内部和边界附近的点,其他函数值hi(j=1,2,...,m,j≠i)是小于零的,因此得到vt=O(t2)。将式(7)替换到式(9)中,得到: (10) 从式(10)可以看出,当所有的hi是负,即点在物体内部时,函数V非常小;当点在物体外部时,V≫t+O(t2);当点在物体边界附近时,V≈t。 考虑当t→0时,则有: (11) 两个正数的和还是正数,一个正数与零的和是正数,两个零的和是零。因此,如果把正数作为逻辑“1”,把零作为逻辑“0”,那么式(11)中vi的“加”操作对应了布尔“或”运算。所以得到: (12) 在水下机器人路径规划中,不期望路径太靠近障碍物。因此,引入一个小的正数Δv作为路径到障碍物的距离控制参数,如果x满足以下不等式: V=∑vi≥Δv或Δv-∑vi<0. (13) 那么这个点一定在由式(13)所确定的障碍物的外部。如果Δv→0,由Δv-∑vi≤0确定的边界将趋近于障碍物的表面。如果一个物体的表面和外部由(h1≥0)∨(h2≥0)∨…∨(hm≥0)确定,那么它的外部和表面同样可以由Δv-∑vi≤0确定,其中Δv→0。x若满足Δv-∑vi≤0,那么x就落在物体的外部。 为了在三个维度上对两栖球形机器人进行建模,必须设定6个独立变量构建环境的空间位置、方向、大小和形状,O=O(x0,y0,z0)代表机器人的几何中心,θ=(θ1,θ2,θ3)代表机器人的定位方向[17-19]。 x=x(x0,y0,z0,θ1,θ2,θ3,v), (14) y=y(x0,y0,z0,θ1,θ2,θ3,v), (15) z=z(x0,y0,z0,θ1,θ2,θ3,v), (16) 其中:x,y,z是机器人边界上的一个点,用于构造没有碰撞条件的机器人,x0,y0,z0是空间位置,θ1,θ2,θ3是空间方向,v是具有两个参数的向量,(t1,t2)用于表示特定机器人的边界点,球形机器人定义如下: ((z-z0)/rz)s/s1=1, (17) x=rxcoss1(t1)coss2(t2), (18) y=rycoss1(t1)coss2(t2),-π/2≤t1≤π/2, (19) z=rzcoss1(t1),0≤t1≤2π. (20) 基于SQP算法,路径规划问题转化为半无限约束优化问题。假设空间中有n个障碍物,则j个障碍物的表面可以表示为[20]: h1(x,y,z)=1,j=1,2,…,n. (21) 整个可用空间可表示为: 1-h1(x,y,z)≤0,j=1,2,…,n. (22) 没有碰撞的必要和充分条件是曲面上所有点都必须无碰撞,获得无碰撞的充分条件是: 1-hj(xloc,yloc,zloc)≤1, (23) 其中: xloc=x(x0,y0,z0,θ1,θ2,θ3,v) yloc=y(x0,y0,z0,θ1,θ2,θ3,v) zloc=z(x0,y0,z0,θ1,θ2,θ3,v). (24) 在路径规划中,配置变量需要一个约束,如公式(25)所示[21-22]: x0l≤x0≤x0u,y0l≤y0≤y0u,z0l≤z0≤z0u, θ1l≤θ1≤θ1u,θ2l≤θ2≤θ2u,θ3l≤θ3≤θ3u. (25) 其中(x0l,y0l,z0l)和(x0u,y0u,z0u)分别是上限和下限,推导得到: 1-hj(rxcoss1(t1)coss2(t2)(cos(θ1)cos(θ2)cos(θ3)-sin(θ1)sin(θ3))- rycoss1(t1)sins2(t2)(cos(θ1)sin(θ3)-cos(θ2)sin(θ2)sin(θ3))+rzsins1(t1)(cos(θ1)sin(θ2))+x0, rxcoss1(t1)coss2(t2)(-cos(θ1)cos(θ2)sin(θ3)-sin(θ1)cos(θ3))+ rycoss1(t1)sins2(t2)(sin(θ1)cos(θ2)sin(θ3)-cos(θ1)sin(θ3))+rzsins1(t1)sin(θ2)sin(θ3)+y0, rxcoss1(t1)coss2(t2)cos(θ1)sin(θ2)+rycoss1(t1)sins2(t2)sin(θ1)sin(θ2)+rzsins1(t1)cos(θ2)+z0≤0. (26) 在方程中,-π/2≤t1≤π/2,0≤t2≤2π。 在非线性规划问题中,目标函数必须具有下限的最小值。目标设置必须使全局最小值可变,二次函数的目标函数表示为: f(x0,y0,z0,θ1,θ2,θ3)=w((x0-x0g)2+ (y0-y0g)2+(z0-z0g)2)+(1-w)((θ1-θ1g)2+ (θ2-θ2g)2+(θ3-θ3g)2). (27) 其最优化点的坐标为(x0g,y0g,z0g),最优化角度为(θ1g,θ2g,θ3g),并且满足方程式: minf(x0,y0,z0,θ1,θ2,θ3)= (x0g,y0g,z0g,θ1g,θ2g,θ3g)=0. (28) 在前面的公式中,w表示用于调整空间位置(x0-x0g)2+(y0-y0g)2+(z0-z0g)2和机器人空间方向(θ1-θ1g)2+(θ2-θ2g)2+(θ3-θ3g)2之间的相对关系的权重,当w=1时计算空间位置。当w=0.5时,空间位置和空间的权重方向必然相等。 为验证两种基于路径规划的GCOP和SQP在水下两栖机器人的路径规划过程中的有效性,使用MATLAB设置了两种算法,从初始起始坐标Ol=(-200,-200,-200)到达目标Ou=(600,600,600)的仿真实验的场景范围。场景空间的长、宽和高为600 cm的立方体形状。 基于SQP算法的不等式Ol≤O≤Ou通过四个参数确保生成的路径在场景内,坐标分布分别在三维平面上的Os=(x0s,y0s,z0s),θs=(θ1s,θ1s,θ1s),Og=(x0g,y0g,z0g) 和θg=(θ1g,θ2g,θ3g) 。GCOP算法的初始时刻设定t=0,Δv=0.000 1,起点坐标为: (x0s,y0s,z0s,θ1s,θ2s,θ3s)= (-200,-200,-200,0,0,0), (29) (x0g,y0g,z0g,θ1g,θ2g,θ3g)= (500,500,500,0,0,0). (30) 目标函数定义为: f=ω[(x0-500)2+(y0-500)2+ (31) 如果满足等式,则该坐标点不会与球形障碍物碰撞。在模拟实验中设置了4个球形障碍物,为确保基于两种算法的准确性。4个障碍物的坐标和方程定义为: (x-200)2+(y-200)2+(z-200)2=502, x2+(y-200)2+(z-200)2=302, (x-400)2+(y-200)2+(z-200)2=302, (x-200)2+y2+(z-200)2=302. (32) 球形机器人的参数为(rx,ry,rz)是对象的几何间隔(s1=1,s2=1.5 表示机器人的形状是球形): rx=5,ry=4,rz=3,s1=1,s2=1.5. (33) 图5为仿真结果(彩图见期刊电子版),在起点和目标点之间有4个障碍。粉色球和灰色球表示不同算法的两栖机器人的运动轨迹。3个蓝色球体和1个红色球体分别代表障碍物。 图5 两种路径规划算法仿真分析Fig.5 Simulation analysis of two path planning algorithms 机器人从起始位置到目标位置经过4个障碍物,两种算法比较,SQP算法在路径规划上更加合理,并在3个采样点处(黄色圆点)离障碍物始终保持了安全距离。但GCOP算法选择的路径在坐标点(-100,190,332.5)处离障碍物较近,如机器人发生小角度偏移,有发生碰撞的危险。所以SQP算法比GCOP算法在安全路径规划的路径控制方面更加有效。而在达到目标坐标位置上,两种算法的误差 Δd=167.5 mm,因此SQP算法在水下路径规划上更具有优势。 为了进一步验证文章所提出算法的有效性,本文设计了基于SQP算法的水下测试实验,实验是在长1 500 mm,宽为1 000 mm,高度为800 mm的封闭水池环境下进行,如图6所示。图中设置了跟仿真环境相匹配的4个球形障碍物,分别设计障碍物的固定坐标位置。机器人从起点出发,激光测距模块和图像采集传感器实时采集障碍物在水中的坐标,并实时调整机器人的运动轨迹,按算法程序中设定的最佳路径移动到目标位置。图7(a)是t=0 s时刻机器人的初始位置,箭头标明了规划的机器人最优路径轨迹。 图6 球形机器人避障实验环境Fig.6 Experimental setup for avoiding obstacles of robot 图7 SQP路径规划算法的实验图片Fig.7 Photoes of path planning by SQP algorithm 图7(b)~7(i)是机器人从t=0 s移动至t=15 s的实际运动轨迹。在实验过程中,采集6个不同的时间点,对机器人y轴和z轴方向的位移变化曲线进行采样,从而判断机器人在最佳路径选择上的稳定性和可靠性。从图8可以看出,机器人分别在第二个和第三个采样点偏移误差较大,误差值达到20 mm,在其余4个采样点误差小于10 mm,这是因为机器人在第二个到第三个采样点主要是对路径的选择阶段,从而影响了机器人的运动形态。机器人的运动轨迹如图9所示。 图8 球形机器人y轴和z轴运动方向误差Fig.8 Kinematic errors of robot in y-axis and z-axis 图9 球形机器人的最佳路径轨迹Fig.9 Optimal path trajectory of spherical robot 本文提出了两种基于路径规划的算法(GCOP和SQP),通过设置4个不同尺寸的球形障碍物使两栖球形机器人可以通过视觉伺服传感器实现避障功能并选择最佳路径。在实验中,设置3个采样点对两种路径规划算法进行评估,基于GCOP算法在(-100,190,500)和(-5,200,345.8)处距离障碍物较近;而基于SQP算法在相对应的采集点处坐标分别为(-100,190,500)和(-160,190,500),相对处于离障碍物较为安全和合理的位置。在终点坐标位置,基于GCOP算法到达预计终点坐标为(500,500,332.5),偏离了预先设定的终点坐标,而基于SQP算法到达终点的坐标为(500,500,500),基本达到预先路径规划的要求。通过3个坐标点的数据显示分析,两个采样点的坐标偏差最优化是要保证距离障碍物的距离在合理范围之内,SQP算法在两个采集点处的障碍物距离更加合理。在第三个终点采样点,两种算法的机器人运动轨迹偏差为167.5 mm。实验表明,对于两栖水下机器人的水下运动控制,基于SQP的路径规划算法比GCOP的路径规划算法更具有优越性。 未来的研究工作会在机械设计和控制方法上持续改进,以实现多机器人的水下多机协作控制与路径规划的最优控制。4.3 SQP控制算法
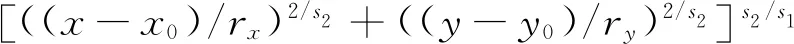
5 实验及结果分析
5.1 仿真实验

5.2 水下实验




6 结 论

