库水位上升对岸坡建筑桩基的稳定性影响分析

阳 波 王子健 周 鹏 武黎明 张佳宁 张 鑫 罗文宇

（1、重庆科技学院，重庆401331 2、重庆工商职业学院，重庆400052）

随着我国库区城市经济社会的快速发展以及建设用地的不足，越来越多的库岸边坡被用作建设用地，而库水位的变化会使岸坡地基的应力状态及水动力状态发生改变，轻则导致建筑物的结构产生变形、开裂，重则导致房屋因地基失稳而垮塌。目前有许多学者已在库水对岸坡稳定性影响方面进行了研究，但涉及岸坡上部建筑物的研究还非常少。刘文月[1-2]对金沙江某岸坡公路进行了有限元分析，研究了路基与库区的距离以及库水位升降速度对路基变形的影响；吴铁营[3]以丽宁公路丽江古城至宁范开元桥段改扩建工程为研究对象，通过有限元软件分析了库水升降速度对库岸桥梁基础的水位位移及沉降值的影响；杨背背[4]基于地质资料和监测资料，归纳总结了库区水位变化对岸坡稳定性及变形的影响。梁学战[5]通过试验与数值模拟相结合对三峡库区典型岸坡的失稳机制进行了研究；王学武[6]对库水升降时的岸坡渗流场变化进行分析，研究了库水对岸坡的影响规律。

1 原理

岸坡土体分为两个部分，分别为浸润线以下的饱和土、浸润线以上的非饱和土，受库水升降影响，边坡表面的孔压会发生改变，进而使土体吸水或者失水，导致非饱和土与饱和土的相对状态发生转变，而这种转变的本质是土体的渗流作用。岸坡渗流包括饱和渗流与非饱和渗流，二者均服从达西定律[7]。

式中k 为渗透系数，i 为水力坡度。在饱和渗流中，渗透系数为定值；但对于非饱和渗流，渗透系数会发生变化。这是因为非饱和土中含有气体，减小了孔隙水的流动空间，使渗透系数减小，因此其渗透系数与饱和度有关，本文采用S.E. Cho[8]等人提出的关系式控制土的渗透系数与饱和度之间的函数关系。非饱和土不仅受到作用于土骨架上的土体净应力作用，还受土体与孔隙水之间的基质吸力作用，因此在进行有限元分析时，应该同时考虑净应力与基质吸力对土体应变的影响。本文采用基于摩尔库伦准则的弹塑性本构模型，其中土体的应力状态采用有效应力进行定义，如式（2）。

式中σ'为有效应力，σ 为净应力，χ 为有效应力系数，在有限元分析中认为其等于饱和度，μw 为孔隙水压，μa 为孔隙气压。

2 有限元模拟

2.1 模型概况

选取某库区典型岸坡及其上部建筑为研究对象，其中边坡底边长140m，高度为50 米，边坡示意图如图1，库区最低水位为145m，最高水位为175m，库水分别以1m/s 和0.5m/s 的速度从初始水位上升至最高水位。

图1 边坡示意图

边坡土体分为两层，材料参数如表1 所示。建筑物位于边坡顶部的平整场地，距离边坡边缘25m，建筑物为采用C30 混凝土的框架结构，材料参数如表1。

表1 材料参数

2.2 模型计算及分析

根据上述条件建立二维饱和- 非饱和渗流模型，首先对初始水位时的模型进行稳态分析，然后将计算得出的土体应力作为初始条件导入边坡中，分别对库水位上升速度为1m/d 和0.5m/d 上升的两种工况进行瞬态分析，得到了岸坡渗流及上部建筑变形的规律。由图2 可知，当库区水位上升时，靠近库区一侧土体的浸润线相对较高，这是因为库水位上升后，库水逐渐向坡体内渗流，但土体的渗流阻力导致坡体内的地下水位不能及时响应库水位的上升。且库区水位上升速度越快，渗流阻力的影响越明显，浸润线左右两端的差值越大。

图2 库水以不同速度上升至最高水位时的浸润线

库水位上升过程中，岸坡的应力状态也会产生较大变化，这是因为库水位以下的坡面会受到库水压力的作用，而随着土体饱和度改变，其土体与孔隙水之间的基质吸力也会发生改变，此外渗流作用还会产生渗流力。在库水上升过程中，岸坡竖向应力最大处逐渐上移，不同库水位时边坡的应力变化如图3、4 所示。

图3 库水位155 时的竖向应力

图4 库水上升至最高水位时的竖向应力

提取岸坡建筑左、中、右三根桩底部的沉降值，绘制曲线如图5、6 所示，沉降值均为正值，因此桩基发生的是隆起。分析图5、图6 可知，靠近库区的桩基沉降值相对较大。从图中还可以看出，水位上升速度越快，在同一时刻其隆起值越大，即桩基变形量与库水上升速度成正相关。此外，对比图5、图6 可以发现库水上升速度越快，桩基之间的沉降差值越大。

图5 1m/s 上升时桩基沉降

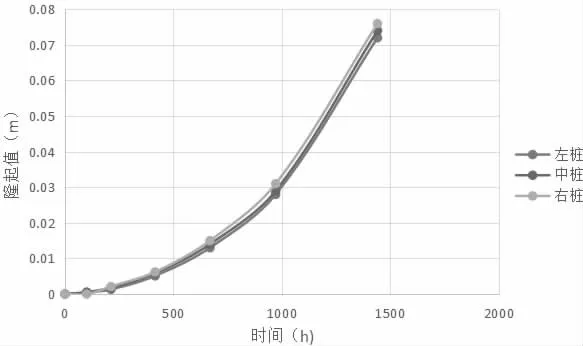
图6 0.5m/s 上升时桩基沉降

3 结论

以某库区某典型岸坡及其上部建筑为研究对象，基于饱和、非饱和渗流原理，采用有限元软件对整体模型进行了流固耦合分析，得出以下结论：

（1）库区水位上升速度越快，岸坡内浸润线左右两端的差值越大；

（2）库水位上升会导致建筑物发生隆起，且隆起值与水位上升速度成正相关；

（3）岸坡建筑距离库区越近，则受库水升降的影响越大。