非制冷微测辐射热计受激光辐照的温度响应

周 冰,贺 宣,刘贺雄,李秉璇,黄富瑜

(陆军工程大学石家庄校区电子与光学工程系,河北 石家庄 050003)

1 引 言

近年来,在大众市场应用的驱动下,非制冷红外探测技术得以迅猛发展。特别是融合了MEMS和IR技术的微测辐射热计,凭借其成本低、重量轻和功耗小的优势而备受人们的青睐,也成为了军队作战侦察、探测的重要途径[1]。与此同时,为了占领信息化作战的制高点,针对红外探测器的激光干扰技术也悄然兴起,并逐步成为了人们关注的焦点。在不同参数激光的辐照作用下,非制冷红外探测器的温度响应是分析激光干扰问题的关键。对这一方向的研究,一方面为激光干扰武器的研发提供理论指导,另一方面为红外侦察系统开发抗干扰功能提供依据,因而具有重要意义。

相比于连续激光的辐照效果,脉冲激光辐照非制冷微测辐射热计带来的温度响应更为复杂,特别是脉冲频率、脉冲宽度和占空比等参数对辐照效果的影响是决定干扰成功的关键。在一定的能量范围内,脉冲激光可以被斩波调制的连续激光等效替代。基于此,本文结合非制冷微测辐射热计的构造和工作机理,分析了像元的温度响应机制,建立了经斩波调制的激光辐照非制冷微测辐射热计的模型。以激光辐照UL01011型非晶硅红外探测器为例,对不同激光参数的辐照效应展开了研究,采用有限元分析的方法进行了仿真,总结出了一定的规律,并归纳出相应的结论。

2 理论分析

非制冷微测辐射热计是红外探测器的核心部件,依托光敏材料制成的空间微观结构实现热辐射信号向电信号转换的功能。当红外波段的光辐照至光敏材料时,除透射和反射的能量之外,被吸收的光能转化为材料的内能。微观上主要表现为三部分[2]:晶格振动产生并传播声子；电子吸收光子引起跃迁到导带；发生激子吸收,逐步转化能量。三者共同作用带来了热激发,获得能量的电子挣脱了原子核的库伦作用,这增加了自由载流子的浓度,从而提高了光敏材料的电导率。

2.1 成像原理

非制冷微测辐射热计主要由三部分组成[3]:光学系统、红外焦平面阵列和电气系统,电气系统包括驱动电路板和图象处理板。目标辐射的远红外光经光学透镜成像于焦平面的像元阵列,像元升温,电阻发生变化,驱动电路板提供偏置电压并逐行采集像元信号进行前处理；图像处理板将传输来的像素信号经一系列后处理最终得到红外图像。为了得到较好的工作性能,非制冷微测辐射热计的像元多为Ⅰ型微桥结构，如图1所示,并利用脉冲式直流电压偏置,采集像元产生的电流信号,经处理即可得到目标区域的红外图像。由于制造工艺的限制,各像元的光电性能有所差异[4],因而需要进行非均匀校正,使得所有像元对目标区域红外辐射的响应性能一致。为了使各像元拥有相等的参照温度,像元下方为恒定温度的衬底(Substrate),它通过连接的热电制冷器(TEC)来实现[5]。

图1 探测器像元的Ⅰ型桥式结构

若像元电阻为R,则其电阻温度系数(TCR)[6]为:

(1)

对于半导体而言,α<0,电阻随着温度升高而减小。在像素值读出的过程中,与像元连接的MOS管起到了采集像元信号的关键作用。由于偏置电阻的存在,使得在恒定大小总偏置电压的作用下,施加在像元上的分压随着其电阻的变化而变化。该电压信号经MOS管线性放大,转化为电流信号,然后被信号放大器采集和使用。MOS管的栅源电压被定义为像元两端电压UR,设其开启电压Ut,漏源电压Uds,跨导系数β。随着温度的升高,UR不断减小,MOS管的漏源电流为:

(2)

该电流信号就是处理成像素值的原始数据。为了保证设备的正常工作,MOS管的线性工作对应的像元温度区间应大于设备的额定温度区间。

2.2 温度响应

对像元的受热情况进行分析,在正常工作的状态下,主要为以下三点:

(1)偏置电压引起的焦耳热。对于50 f/s或60 f/s成像机制的探测器,像元相应地每秒受到偏置作用50或60次,每次作用的时间低于100 μs。由于作用时间远远小于偏置周期,焦耳热引起的像元温升量不大,可以忽略不计。

(2)周围环境的散热作用。一方面,像元通过支撑腿与衬底连接,受热升温后不断向衬底传导热量；另一方面,像元自身的热辐射也造成了热量的损失。一般情况下,像元组成了红外焦平面阵列被置于金属封装的真空环境,因此可以忽略空气对流的影响。

(3)激光辐照,使其温度升高。设像元的比热容为C,对衬底的热导率为G,忽略热辐射损失的能量,当功率恒为P0的连续激光作用于单像元时,有热平衡方程:

(3)

其中,η是吸收率;T0是像元的初始温度,也是衬底为红外焦平面阵列提供的参照温度。解这个一阶微分方程,得到稳态下的温度:

(4)

假设作用于像元的激光受到占空比δ,频率f的斩波调制,图2为光能随时间的变化情况,其中k=1/f为斩波周期。

图2 经斩波调制的激光功率

因此,在第n个周期内,温度变化情况可描述为:

(5)

3 热分析模型的建立

基于实际设备的参数及工作条件,利用Solid works软件建立三维模型,并设定仿真条件,利用Ansys Workbench展开有限元分析。结合设备实际的工作温度区间[7],设定斩波调制频率、占空比和激光功率分别变化的条件,研究这些参数对非制冷微测辐射计温度响应的影响。值得注意的是,该方法已经通过大量数值验证是正确的[8-10]。

3.1 建立模型

基于法国ULIS公司设计的UL01011型320×240 α-Si非制冷微测辐射热计的相关参数[11],建立了3-D模型,如图3所示。为了便于计算,将像元的尺寸做了微小调整。

图3 非制冷微测辐射热计的3-D模型

该设备的相关参数如表1所示[11],在阵列进行非均匀矫正时,偏置电压U会根据各像元的热电性能被设定为不同的值。像元采用图1的结构,由金属真空封装。

表1 UL01011型320×240 α-Si非制冷微测辐射热计的典型参数

3.2 仿真条件

非制冷微测辐射热计激光辐照效应的关键在于像元的温度,因此采用Ansys Workbench软件的瞬态热分析(Transient Thermal)模块展开研究[12-14]。

3.2.1 材料参数

为了使模型具有表1的热物理性质,做如下处理:

将模型沿虚线处区分开，如图3所示,使模型的微桥面与两桥腿分别被定义成两种材料。微桥面主要功能为吸收光能,温度升高,并通过偏置电路提供像素值。硅材料的质量密度为ρ=2.33 g/cm3,在300 K的温度下热导率k=0.151 W/(mm·K)。将光敏材料的热熔率(Heat Capacity)定义成:

(6)

其中，Vdeck是微桥光敏材料的体积。在热分析中,桥腿的作用主要为传导热量,将它的热导率定义为:

(7)

其中,S和L分别是在热传导方向上,微桥腿的截面积和长度。

3.2.2 载 荷

根据以上分析,该模型受到的热载荷作用主要为两项。

(1)像元吸收的光能。像元的光敏材料厚度为0.5 μm,远小于硅对于远红外激光的吸收厚度(0.7 mm)[2]。然而,依托微桥结构形成的谐振腔[15],光敏材料对激光的吸收率达到了0.8。为了简化研究,忽略光敏材料对激光吸收率的纵向差异,认为激光在材料内部发生了均匀吸收。从这个角度来看,它也可以等效为材料自身产生的体热源。该热源大小为:

(8)

(2)在微桥两脚底,固定于衬底的两个接触面发生散热。在像元正常工作的情况下,被TEC制冷的衬底保持恒温来提供参照温度,因而该载荷等效为接触面上固定大小的温度,设该温度T0=300 K。

3.2.3 仿真内容

为了研究斩波调制频率f对温度响应的影响,设定了仿真1～5的条件,根据公式(8)的计算Pe,参数如表2所示。

表2 第1组仿真实验参数

为了研究斩波调制占空比δ对温度响应的影响,设定了仿真6～10的条件,参数和Pe计算结果如表3所示。

表3 第2组仿真实验仿真参数

为了研究激光功率p0对温度响应的影响,设定了仿真11～16的条件,参数和Pe计算结果如表4所示。

表4 第3组仿真实验参数

4 仿真结果及分析

首先,为了确保模型的正确无误,对模型施加未经调制的激光载荷,将仿真结果与公式计算结果进行对比。功率为P0=7.8×10-6W,对应Pe=5 W/mm3。按照式(4)计算出模型稳态的温度为T=362.50 K,模型经Ansys仿真得到的结果如图4,模型在稳态下的最高温度为363.13 K,存在误差是因为式(7)的计算中取了近似值。模型得证。

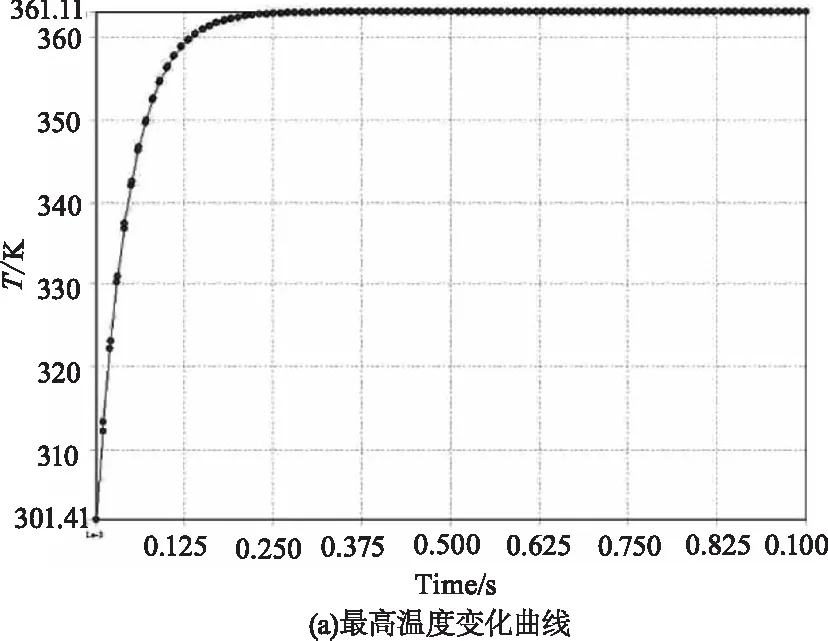
图4 持续激光热源仿真的模型温度

在Ansys中,将APDL命令插入Workbench的瞬态热分析模块中,实现了斩波调制函数的定义。插入的APDL命令为[16]:

用数值代替Pe,f,k,δ录入软件中,对结果进行了归整。

4.1 调制频率的影响

第一组仿真结果中,根据模型稳态温度振荡的极高点和极低点,计算出平均值,如表5所示。

表5 第一组仿真的稳态温度振荡值

对温度振荡的均值与调制频率进行曲线拟合,得到图5和关系式:

T=575.2f-1.011+363.2

(9)

式(9)表明,温度振荡均值与调制频率成负指数关系。

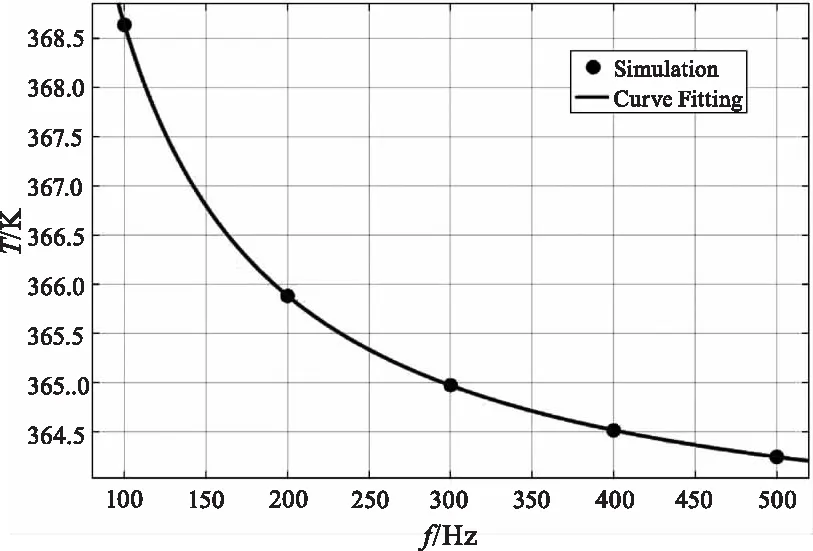
图5 第一组仿真温度振荡的均值与调制频率的曲线拟合

4.2 占空比的影响

第二组仿真结果中,根据模型稳态温度振荡的极高点和极低点,计算出平均值,如表6所示。

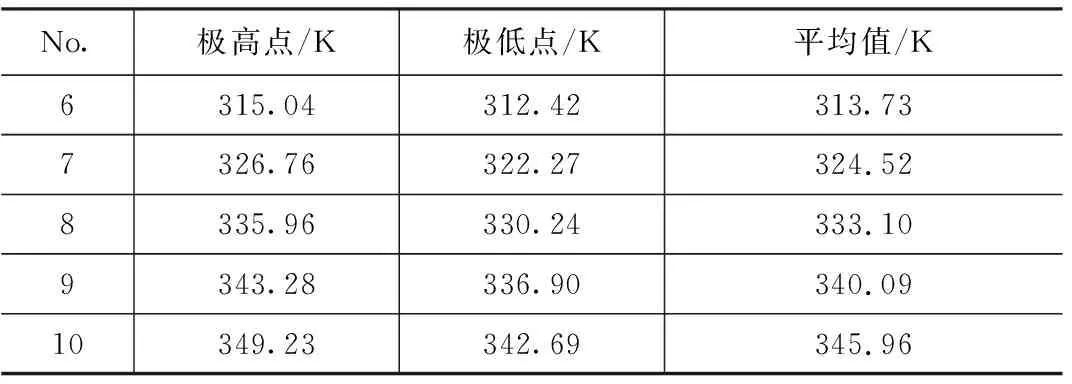
表6 第二组仿真的稳态温度振荡值

对温度振荡的均值与占空比进行曲线拟合,得到图6和关系式:

T=84.26δf0.474+285.5

(10)

图6 第二组仿真温度振荡均值与占空比的曲线拟合

由此可知,温度振荡的均值与占空比成正指数关系。

4.3 激光功率的影响

第三组仿真结果中,根据模型稳态温度振荡的极高点和极低点,计算出平均值,如表7所示。

表7 第三组仿真的稳态温度振荡值

对温度振荡均值与激光功率做数据拟合,得到图7和关系式:

T=8.767×105P0+300.7

(11)

图7 第三组仿真温度振荡均值与占空比的曲线拟合

显然,稳态温度振荡均值与激光功率成线性关系。

4.4 各因素影响的对比分析

取温度升高量ΔT=T-T0=T-300,则式(9)～(11)可依次转化为:

ΔT=575.2f-1.011+63.2

(12)

ΔT=84.26σ0.474-14.15

(13)

ΔT=8.767×105P0+0.7≈8.767×105P0

(14)

由式(12)～(14)可以看出,斩波调制的激光辐照像元时,温度升高量的震荡均值同调制频率成负指数关系,与占空比成正指数关系,与激光功率成倍率关系。

5 结 论

本文在介绍非制冷微测辐射热计的结构组成和工作原理的基础上,立足UL01011型320×240 α-Si探测器的实际参数建立了激光辐照模型,结合理论推导公式进行了验证；并改变辐照激光的不同参数实施仿真,对各组仿真结果中稳态温度均值与激光参数进行了曲线拟合,通过分析得到结论:功率稳定的连续激光经斩波调制后辐照至非制冷微测辐射热计时,稳定状态下像元温度升高量的振荡均值与三个参数分别成以下关系:

与调制频率f成指数关系,且随着f的增大而减小；与占空比δ成指数关系,且随着δ的增大而增大；与激光功率成线性关系。