矿井空巷道无线信道特性分析与仿真*

姚述福,余伟健,2*

(1.湖南科技大学 资源环境与安全工程学院,湖南 湘潭 411201; 2.湖南科技大学 煤矿安全开采技术湖南省重点实验室,湖南 湘潭 411201)

矿井隧道是一种复杂的受限空间,电磁波在隧道中受传播频率、天线极化、隧道截面大小、隧道壁反射、隧道壁粗糙度及倾斜度等因素的综合影响,其传播特性有别于地面[1-6].由于矿井巷道环境复杂恶劣,不利于电磁波的传输,所以地下巷道电磁波传输理论的发展不如地面迅速.但随着通信技术更新换代,近年来对地下电磁波传输理论的研究也发展迅速,运用到地下矿井的通信技术也逐渐完善.

目前矿井隧道的截面形状大多类似于矩形,矿井隧道的粗糙面及隧道中大量机电设备的存在会产生大量多路径信号,对电磁波在巷道中传输时产生极大的损耗,严重影响通信系统信号质量[7].为了简化研究,本文仅分析电磁波在矿井空巷道(巷道内不存放任何物体)中的传播特征.

仿真研究空巷道中电磁波传播时,只就巷道本身的特性,如矿井巷道的截面大小、巷道壁对电磁波的吸收、折射等因素来研究电磁波的传输损耗.这种研究对矿井巷道电磁波的传输提供了理论基础,有相当不错的参考价值.

1 矿井巷道中电磁波传播理论

在文献[8]中提到的波模匹配法,是19世纪出现的一种针对煤矿巷道电磁波传播理论的研究方法.这种方法的优点是建模简单,但是在现实矿井中却难以运用,这是因为矿井巷道环境复杂,真正建立一个符合实际矿井巷道的电磁波传播模型是非常困难的.现有的国内大部分巷道电磁波研究[9-12]也都是研究简化的电磁波模型.

1.1 经典电磁波传播理论

研究地下巷道中电磁波的传输理论,必不可少的是经典Maxwell(麦克斯韦)方程组.麦克斯韦方程组是麦克斯韦在总结了库仑、安培、法拉第等人的实验定律和麦克斯韦位移电流概念的基础上于1873年提出来的,这为后来的电磁波研究提供了理论基础.Maxwell方程组的微分方程如下[7]：

(1)

式中：H为磁场强度,A/m;D为电通量密度,C/m;J为电流密度,A/m2;E为电场强度,V/m;B为磁通量密度,Wb/m2;ρ为电荷密度,C/m3;ε为介电常数；ε0为自由空间的介电常数；εr为相对介电常数;μ为磁导率；μ0为自由空间的磁导率；μr为相对磁导率.

由Maxwell方程组可以推导出单色波的齐次亥姆霍兹(Helmholtz)波动方程[7]：

(2)

式中：k2=w2με,w为复数.其中k为电磁波的空间频率,在直角坐标系有

(3)

将Maxwell方程组和亥姆霍兹(Helmholtz)波动方程进行结合可得到方程组[7]：

(4)

式(1)～式(4)为矿井巷道电磁场求解提供了重要理论基础.

1.2 Marcatili (马可梯里)近似分析法

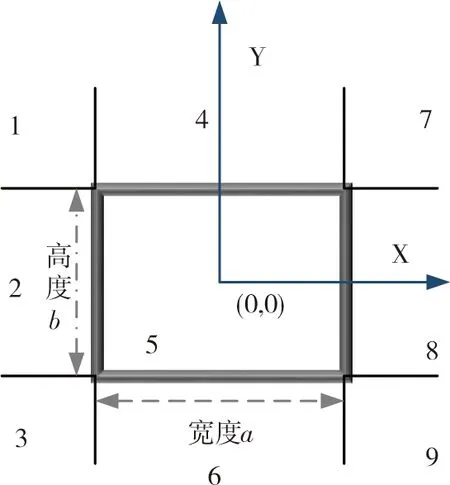
图1 巷道Marcatili 近似分析法

2 电磁波在矿井巷道中传播的能量损耗

矿井巷道作为一种复杂的电磁波传播介质,使得电磁波的传播环境变得比地面上更加恶劣.由于电磁波不是在真空中传播,其自身能量会受到衰减.不同于地面上广阔的传播空间,地下矿井的传播范围急剧缩小到几十平方米的空间,也使得电磁波传播时折射、反射次数大大增加,加剧了电磁波本身的能量损耗.本文对几种矿井巷道中典型的电磁波传播能量损耗进行分析并且仿真.

2.1 电磁波传输模的衰减损耗

矿井巷道壁的组成成分一般比较复杂,而且矿产属性不同,巷道壁的导电率也各不相同.在研究矿井巷道电磁波传播模型时,经常忽略导电率对电磁波传输的影响,而利用模式匹配法去研究电磁波的衰减公式.光学中光的模式包括基模和高次模,但有些电磁波研究者只考虑基模这一种模式,这与矿井巷道中基模和高次模同时存在相违背.所以本文根据色散条件[7]式(5)对基模和多波模进行研究.

(5)

(6)

式中：l为电磁波的传播距离;ε1为巷道两侧壁介电常数；ε2为巷道顶底壁介电常数;a为巷道的宽度；b为巷道的高度.

(7)

2.2 巷道壁倾斜造成的倾斜损耗

由于巷道壁不是水平光滑的,存在一定的倾斜角度,虽然角度值一般很小,但是对电磁波在矿井巷道传输时仍造成了一定损耗,称为倾斜损耗.设空矩形巷道壁的倾斜角为θ,根据文献[12],两侧壁电磁波损耗因子η1和顶底壁损耗因子η2分别为

(8)

电磁波的倾斜损耗因子为这两者的乘积.当巷道中电磁波传输距离为l,电磁波发生反射的次数为

(9)

所以巷道中单波模的倾斜损耗为

(10)

同理可得多波模的倾斜损耗为

(11)

2.3 巷道壁粗糙造成的粗糙损耗

图2 巷道壁电磁波折射图

巷道壁组成成分复杂,由于天然形成以及后续的开采,使得矿井巷道壁表面坎坷不平,电磁波在巷道传播时会入射到粗糙巷道壁的表面而发生折射,对电磁波产生了损耗,称为粗糙损耗.为了简化分析,本文用均值为0，方差为δ2的高斯分布来描述巷道壁的粗糙程度.ΔH为巷道壁的平均高度,θ为电磁波的入射角,如图2所示.

根据瑞利判断法,

(12)

一般认为巷道壁表面是粗糙的,根据文献[12],单波模的入射角满足公式

(13)

由于θ值很小,根据三角函数有

sinθ=θ=tanθ.

(14)

折射波的损耗参数β[12]为

(15)

根据以上公式,可以推导出单波模的粗糙损耗为

(16)

同理可得多波模的粗糙损耗为

(17)

3 巷道电磁波传播特性仿真分析

选择空矩形巷道(内部不摆放任何设备)仿真模型的各项参数如下：巷道总长度=150 m,巷道截面宽度a=4.0 m,巷道截面高度b=3.5 m, 巷道两侧壁介电常数ε1=8 F/m, 巷道顶底壁介电常数ε2=12 F/m,巷道壁平均高度ΔH=0.01 m,巷道壁倾斜角θ=3°.

图3为多波模传播条件下的衰减损耗.由图可以看出,当电磁波频率处于200～300 MHz时,水平极化模和垂直极化模的衰减损耗最大.随着电磁波频率的不断增大,水平极化模和垂直极化模的衰减损耗不断减少,最终趋向于零,这是由于多波模阶数并不随着电磁波频率的增加而增加.在实际传播环境中,单波模与多波模是同时存在的,电磁波波模数变得更加复杂,所以我们选择电磁波的频率时必须考虑其他因素,并不是频率越高,衰减损害就越小.

图4为电磁波倾斜损耗随电磁波频率变化曲线.由图4可以看出,单波模的倾斜损耗随电磁波频率的增加而增加,增长速度较慢,呈一次线性关系,这是由于电磁波频率增加时,其入射到巷道壁上的入射角将变小,则传播相同距离经历的反射次数也随之减少,因此粗糙损耗会降低;多波模的倾斜损耗随电磁波频率的增加而快速增加,这是因为电磁波倾斜损耗与频率的平方成正比.当电磁波频率为1.0 GHz时,曲线增长急速,因此选择巷道电磁波传播频率必须小于1.0 GHz.

图3 多波模衰减损耗

图4 倾斜损耗随电磁波频率变化曲线

图5 粗糙损耗随电磁波频率变化曲线

图5为电磁波倾斜损耗随电磁波频率变化曲线.由图5可以看出,单波模的粗糙损耗随电磁波频率的增加而减小,最终趋向于0 Hz,减小率在100～200 MHz内发生改变;多波模的粗糙损耗随电磁波频率的增加而增加.与图4对比可以看出,巷道中电磁波倾斜损耗比电磁波粗糙损耗严重得多,这是由于在电磁波粗糙损耗中,入射角的相位是不会发生改变的,而巷道倾斜,会使电磁波的波模相位发生改变,使得电磁波在巷道壁每次反射时能量损耗都不相同.因此在分析具体巷道电磁波传输损耗时,必须重点考虑巷道电磁波的倾斜损耗.

图6为巷道电磁波总传输损耗随电磁波频率变化曲线.由图6可以看出,单波模的总传输损耗随电磁波频率的增加而减小,当频率为0～500 MHz时,总传输损耗减小十分迅速,当频率大于1.0 GHz时,总传输损耗几乎不变;多波模的总传输损耗与电磁波频率呈抛物线关系,总传输损耗先急速下降再急速上升,频率为1.0～1.2 GHz时总传输损耗达到一个最小值.

图7为巷道截面尺寸对电磁波总传输损耗的影响.当巷道截面宽度为4.0 m,高度为3.5 m时,电磁波总传输损耗在频率为1.0～1.2 GHz时达到最小值;当巷道截面宽度为5.0 m,高度为4.5 m时, 电磁波总传输损耗在频率为0.8～1.0 GHz时达到最小值;当巷道截面宽度为6.0 m,高度为5.5 m时,电磁波总传输损耗在频率为0.7～0.9 GHz时达到最小值.

图6 总传输损耗随电磁波频率变化曲线

图7 巷道截面尺寸对总传输损耗的影响

根据以上仿真结果可以得到：在本文分析的矿井巷道电磁波3种不同传播损耗中,在电磁波频率小于0.5 GHz时,电磁波自身损耗占主要部分;当电磁波频率达到1.0 GHz后,电磁波自身损耗逐渐趋于一个稳定值,而电磁波粗糙损耗和电磁波倾斜损耗逐渐快速增加,其中电磁波倾斜损耗在总的电磁波传播损耗中占主导地位;在3种不同截面巷道中,电磁波总传输损耗最小是在截面面积最大的巷道中,说明在矿井巷道中,电磁波传播空间越广阔,传输损耗越小,这与电磁波在矿井巷道中发生折射的次数密切相关.所以,综合以上的仿真结果,本文选取1.0 GHz频率段的电磁波作为矿井巷道中最佳载波频率.

4 结论

1)电磁波传输模自身损耗远远低于矿井巷道对电磁波的损耗,所以实际环境中必须优先考虑矿井巷道各方面因素.

2)巷道中电磁波倾斜损耗在3种电磁波损耗中占主导地位,尤其电磁波处于高频时,其倾斜损耗呈几何倍数增长.

3)矿井巷道中,电磁波传播空间越广阔,传输损耗就越小.

本文仅从理想空矩形巷道这一种传输模型进行了分析,这与实际矿井巷道错综复杂的电磁波传输环境存在很大的不同.对于矿井巷道无线信道特性的分析还需继续深入研究.