交通荷载作用下钢弹簧浮置板隔振道路设计参数研究
邹锦华 李碧坤 陈伟 陈海斌 黄龙田 邹超


摘要:為降低城区道路汽车荷载对建筑结构的振动影响,设计一种新型钢弹簧浮置板隔振道路,对浮置板的动力学设计参数进行研究。在浮置板缩尺模型有限元试验验证的基础上,选取浮置板长度、厚度、弹簧刚度、弹簧支承间距4个参数及不同水平值,进行正交试验,建立81个样本的三维有限元模型。采用模态分析法,研究各参数对浮置板固有频率和振型的影响;实测交通荷载激励,分析激励作用下浮置板结构在时域和频域的响应,并通过Z振级和插入损失探讨浮置板结构各参数的减振效果。结果表明:各样本基频主要分布在4~10 Hz之间,基频直接影响钢弹簧浮置板的隔振性能;随着浮置板长度的减小、厚度的增大、弹簧刚度的减小、支承间距的增大,浮置板结构的隔振效果明显提高;交通荷载激励下,浮置板结构振动放大频段位于基频附近及14~18 Hz范围;VLz振级在0~18 Hz范围内随频率增大而增大,之后随频率增大而降低,但未超过72 dB;对于0~40 Hz范围内的振动响应,样本最大减振量为40.6 dB,基频处放大量最大为17.4 dB。
关键词:交通荷载;钢弹簧浮置板道路;模态分析;振级;插入损失;设计参数
中图分类号:U416.0 文献标志码:A 文章编号:20966717(2020)04012411
收稿日期:20190823
基金项目:广东省科技计划(2015B090901054);广东省交通运输厅科技项目(科技201702013)
作者简介:邹锦华(1975 ),男,副教授,博士,主要从事结构、桥梁和隧道振动与控制研究. Email: zoujinhua@gdut.edu.cn。
Received:20190823
Foundation items:Science and Technology Project of Guangdong Province (No.2015B090901054); Science and Technology Project of Department of Transportation of Guangdong Province (No. 201702013)
Author brief:Zou Jinhua (1975), associate professor, PhD, main research interests: vibration and control of structure, bridge and tunnel, Email: zoujinhua@gdut.edu.cn.
Design parameters study of vibration isolation road of steel spring floating slab under traffic load
Zou Jinhua1, Li Bikun1, Chen Wei2, Chen Haibin2, Huang Longtian2, Zou Chao1
(1.School of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou 510006, P.R. China;2.Architectural Design and Research Institute of Guangdong Province, Guangzhou 510010, P.R. China)
Abstract: In order to reduce the influence of vehicle loads on the vibration of building structure, a new type of steel spring floating slab vibration isolation road was designed, and the dynamic design parameters of floating slab were studied. On the basis of finite element test verification of the scale model of floating slab, four parameters were selected and orthogonal tested, including length and thickness of floating slab, spring stiffness and support spacing. Total of 81 cases of corresponding 3D finite elements were established. The modal analysis method was used to study the influence of various parameters on the natural frequency and vibration mode of the floating slab. The traffic load excitation was measured, and the response of the floating slab structure in the time domain and the frequency domain was analyzed, and the vibration damping effect of each parameter of floating slab structure is discussed by Z vibration level and insertion loss. The results show that the fundamental frequency of each sample is mainly distributed between 4 Hz and 10 Hz. The fundamental frequency directly affects the vibration isolation performance of the steel spring floating slab. With the decrease of the length, the increase of the thickness, the decrease of the stiffness of the spring and the increase of the spacing of the supports, the isolation effect of the floating slab structure is obviously improved. The vibration amplification frequency band of the floating slab structure is located near the fundamental frequency and in the range of 14~18.0 Hz under the traffic load excitation. The VLz vibration level increases with increasing frequency in the range of 0~18 Hz, and then decreases with increasing frequency, but does not exceed 72 dB. For the vibration response within the range of 0~40 Hz, the maximum amount of vibration reduction in all samples is 40.6 dB, and the maximum amount of emission at the fundamental frequency is 17.4 dB.
Keywords:traffic load; steel spring floating slab road; modal analysis; vibration level; insertion loss; design parameters
城市道路交通发展带来的振动和噪声问题,对沿线居民和临近建筑等造成很大的影响,成为社会关注的焦点。广州番禺万博商务中心部分结构顶板直接位于市政道路下方,交通荷载引起的结构振动对内部空间商业活动和居民生活产生了不利影响,需对市政道路采用减隔振措施。为降低汽车荷载对下部结构的低频振动,参考轨道交通钢弹簧浮置板的成功经验,设计一种钢弹簧浮置板新型隔振道路。
目前,对市政道路采用钢弹簧浮置板进行隔振的研究尚未见相关文献报道,但对轨道交通浮置板研究很多。如:Lombaert等[1]建立了浮置板轨道三维有限元模型,采用模态分析方法研究了浮置板轨道的设计参数。Hui等[2]采用三维有限元模型研究了浮置板与高架结构箱梁的耦合振动及避免高阶共振的措施。李增光等[3]将浮置板简化为自由边界的Kirchhoff薄板,利用动柔度法建立二维浮置板轨道的频域模型,研究了浮置板的高阶模态。刘维宁等[4]进行了钢弹簧浮置板轨道的低频特征试验,研究了弹簧刚度和支承间距等设计参数对低频振动特性和隔振性能的影响。韦红亮等[5]分别采用有限元和现场试验方法,从时频域角度对高架钢弹簧浮置板轨道结构的减振特性进行了分析。王颖轶等[6]利用车轨耦合动力学研究了短型浮置板的传递特性和板下结构参数对于振动响应的影响。蒋吉清等[7]建立剪力铰连接条件下钢弹簧浮置板轨道模型,研究剪力铰的减振效果和参数优化。韦凯等[8]建立车辆钢弹簧浮置板轨道垂向耦合随机振动频域分析模型,探讨了钢弹簧浮置板轨道频域随机振动的影响规律及设计参数敏感性。黄强等[9]利用振型叠加法比较了质量块、Euler梁和短梁3种轨道模型的振动响应差异和减振特性。李林峰等[10]建立了二维车辆轨道动力有限元模型,对比和分析了普通整体道床和钢弹簧浮置板轨道在冲击荷载、移动常力和移动列车荷载作用下结构的振动响应,通过插入损失评价了钢弹簧浮置板轨道的减振效果。杨文茂等[11]建立地铁车辆轨道桥梁耦合系统动力分析模型,对深圳地铁6号线浮置板轨道U型梁系统的固有频率以及动力特性、系统共振可能性进行了研究。李小珍等[12]建立列车轨道耦合振动频域模型,采用有限元法进行箱梁振动分析,探讨钢弹簧浮置板轨道对箱梁振动声辐射的影响,并结合声学边界元法进行箱梁声辐射分析。
上述虽然已对轨道交通浮置板参数的研究很多,但由于振源不同、道路与轨道结构的差异,市政道路隔振与轨道交通的隔振有着很大的差别。市政道路浮置板由于路面较宽和不宜设置过多接缝等原因,长度和宽度都很大,因此,浮置板道路结构本身的动力性能及设计参数也需进一步优化确定。笔者根据提出的钢弹簧浮置板隔振道路的特点,通过正交试验方法,选取浮置板长度、浮置板厚度、弹簧刚度、支承间距4个参数及不同水平值,建立相应的81个浮置板三维有限元模型。在缩尺模型试验验证的基础上,采用模态分析方法[13]对钢弹簧浮置板道路结构进行动力特性研究,获得固有频率和振型。实测交通荷载激振源,从时域和频域两个角度分析浮置板减振结构在实测交通荷载作用下的响应,并通过Z振級和插入损失来研究不同参数水平对结构隔振性能的影响。从而对不同结构参数下钢弹簧浮置板道路系统隔振性能做出评价,为新型钢弹簧浮置板隔振道路的工程应用提供参考。
1正交试验设计
采用正交试验法对浮置板结构设计参数进行选取。因万博中心地下空间上方市政道路宽度为10 m,故浮置板宽度固定为10 m。正交试验选取浮置板长度、浮置板厚度、钢弹簧刚度、支承间距4个参数进行分析,其中,浮置板长度9个水平值,浮置板厚度5个水平值,钢弹簧刚度和支承间距各4个水平值,如表1所示。
若对表1参数完全组合,需要进行9×5×42=720次试验。为了既能够减少试验的次数又能够全面反映试验的内在规律,利用正交试验法进行优选。对上述钢弹簧浮置板道路结构不同水平参数,使用混合水平正交试验表设计试验,优选出81个代表性的试验样本,建立有限元模型。
2有限元模型试验验证
进行浮置板参数分析之前,首先对有限元分析模型进行试验验证。利用室内试验对钢弹簧浮置板缩尺模型进行锤击试验,得到固有频率,并与通过有限元软件建立的钢弹簧浮置板缩尺模型的计算结果对比,验证有限元分析方法的合理性和可靠性。
弹簧浮置板试验模型长3 200 mm,宽1 600 mm,厚170 mm,采用C40混凝土,HRB335钢筋,按正常使用极限状态进行结构设计;混凝土材料的质量密度为2.6×103 kg/m3,弹性模量为3.25×104 MPa,泊松比为0.2,结构阻尼比为0.05。钢弹簧刚度为5.3 kN·mm-1,间距按0.65 m取值,分别为4、6、8、10钢弹簧。
采用ANSYS软件对钢弹簧浮置板建立三维有限元模型,浮置板和钢弹簧分别采用Shell63单元和Combin14单元。钢弹簧隔振器的构造决定了浮置板只能产生竖向变形,因此,将模型中的Combin14单元除竖向以外的其他自由度约束。考虑到市政道路两侧及相邻浮置板对四周位移的约束,对浮置板模型两端x方向进行约束和两侧y方向进行约束;钢弹簧下端用一般支承将6个方向的自由度全部约束。图1为钢弹簧浮置板锤击试验和6个钢弹簧时的计算模型和平面图。
试验得到钢弹簧浮置板的固有频率,如表2所示。
由表2可以看出,各种间距钢弹簧浮置板试验基频与有限元计算得到的频率基本一致,各试验值/模拟值误差范围均小于10%;数值模拟结果较试验结果偏小,其最大差值为4弹簧浮置板的0.6 Hz;可以认为有限元模型能基本反映结构的动力特性,采用该有限元建模方法对钢弹簧浮置板各参数进行分析是可靠的。
3频率与振型
用上述有限元分析方法对正交试验的81个样本建立浮置板三维有限元模型,图2为浮置板长度30 m、厚度0.30 m、钢弹簧刚度3.6 kN/mm、支承间距3.0m时的有限元分析模型。
3.1固有频率
应用ANSYS软件对各样本进行模态分析,计算得到各因素不同水平下的竖向固有频率和振型。限于篇幅,仅选取表3所列20个样本的前6阶固有频率与结构参数水平关系来说明,其余样本和更高阶频率省略。
在该弹簧设置方式(板厚、弹簧刚度不变,弹簧支承间距为3 m)下,浮置板长度是影响其隔振性能的一个重要因素。由表3可以看出,当其他3个设计参数
不变时,浮置板固有频率随着长度的增加而降低,且阶数越高固有频率降低的幅度越大。浮置板的长度由8 m增长到45 m时,其各阶固有频率减小幅度明显,例如长度为8 m时的第6阶固有频率为57.811 Hz,长度增加到45 m时,第6阶固有频率为26.979 Hz;当板长大于45 m时,其固有频率减小趋势减缓。
厚度对于浮置板的第2阶及更高阶固有频率的影响比较大,厚度对浮置板固有频率的影响主要是由于质量的变化,质量增大时,固有频率降低。浮置板第1阶固有频率随着厚度的增加逐渐递减,且降幅比较明显,如厚度为750 mm的浮置板比厚度为150 mm的浮置板的基频降低了3.828 Hz;但以后各阶固有频率反而增大,且阶数越高,增幅越大,厚度为150 mm的浮置板比厚度为750 mm的浮置板第2阶固有频率增大了7.54 Hz,第6阶固有频率增大了34.997 Hz。
浮置板固有频率随着弹簧刚度的增大而增大,弹簧刚度为1.9 kN/mm时比弹簧刚度为7.0 kN/mm时,浮置板的基频降低了2.717 Hz,效果显著;当弹簧刚度小于5.3 kN/mm时浮置板基频小于5.0 Hz。浮置板自振频率随支承间距的减小而增加,弹簧布置越密集,结构整体刚度也越大,自振频率的变化受弹簧刚度影响。支承间距从3.0 m变化到1.2 m,其1阶自振频率增加了4.769 Hz,且随着阶数的增高增幅越大,其第6阶固有频率增加30.85 Hz。因此,在浮置板设计过程中应该从浮置板质量与钢弹簧刚度两方面着手,选择长度在60~90 m之间,厚度为45c m,弹簧刚度较大且支承间距较小的浮置板。
3.2振型
图3列出了3个样本的前6阶竖向振型。从图3中可以看出,浮置板的长度不同,其振型也不相同。浮置板长度为45 m的样本一第1阶振型与长度为75 m的样本三第1阶振型相似,而样本二和样本三的第6振型以竖向弯曲为主、样本一的第6阶振型以扭转为主。由此可以得出,浮置板长度较小时,第1阶振型浮置板以竖向平动为主,第6阶振型以扭转为主;随着浮置板长度的增加,第1阶~第5阶振型基本相似,第6阶以上振型区别较大。
4交通荷载作用下浮置板隔振性能分析
4.1交通荷载激励源
测试地点选为番禺区万博商务中心邻近的南大路。南大路为单向两车道城市次干路,设计速度40 km/h,由西向东下穿新光快速路,东接番禺大道北路,路面平整度较好,为单层水泥混凝土路面上铺沥青混凝土面层。由于靠近番禺区万博中心和主干道,车流量较大,非机动车多,车速较低。主要车型为小汽车、小货車、公交车,偶尔有大货车通行。
混合车流虽然车况路况复杂,无法分析车辆运行速度、型号及载重对于振动响应的影响规律,但可以包含设计车速内各种车辆型号、载重的数据。测试时选取早高峰(7:00—9:00)、午间(12:00—14:00)、晚高峰(18:00—20:00)3个时段,每一时段2 h,共6 h;同时,通过摄像机记录道路上行驶的随机车辆。图4为节选的5 s时长的交通荷载激励源时程和频谱曲线,表4为路面振动加速度响应峰值和主频。
从图4和表4可看出,混合车流时早、中、晚高峰时段竖向振动时程的加速度峰值分别为4.27、6.57、11.04 mm/s2。混合车流时的竖向振动频率范围为9.5~39.0 Hz,但峰值频率在10.0~20.0 Hz之间。
4.2时域和频域
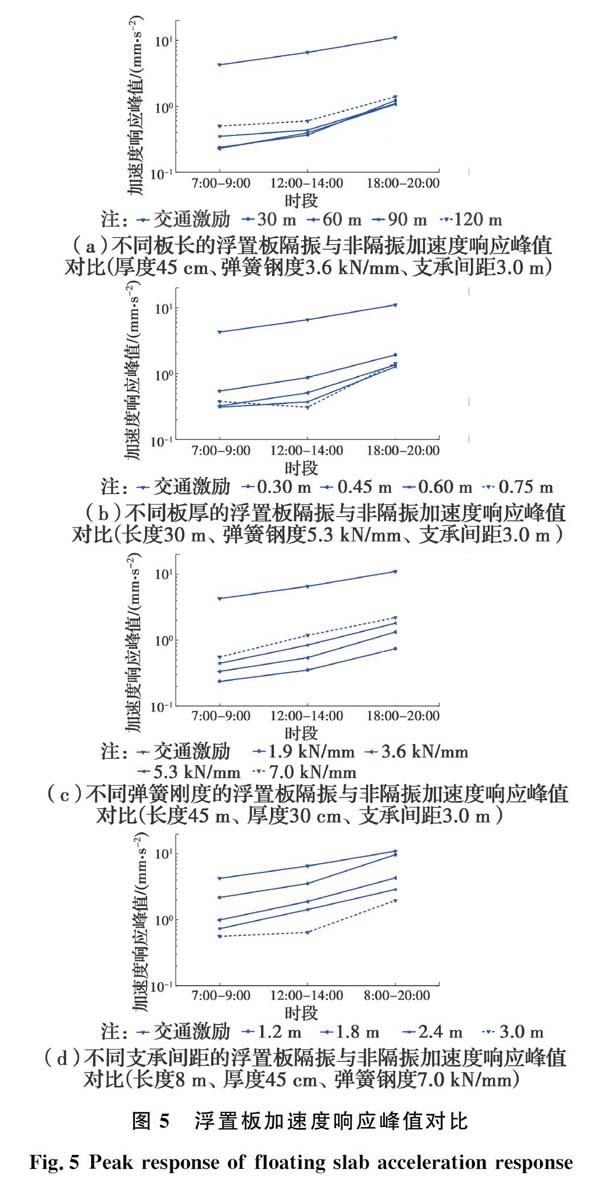
表5为3个交通高峰时段荷载激励下计算得到的部分样本加速度响应峰值。从表5可以看出,早、中、晚高峰时段混合车流作用下浮置板竖向振动加速度峰值主要集中在0.23~2.18、0.31~3.55、0.74~9.76 mm/s2。图5为4种参数下隔振前后加速度峰值的变化。
从表5可以得出,3个交通高峰时段内,4种长度的浮置板减振值范围分别为88%~95%、91%~94%和87%~90%。长度为30~60 m时,浮置板结构对早高峰和午间两时段的减振值达94%。当板厚为30 cm时,早高峰、午间和晚高峰3个时段的减振值分别为92%、87%和83%,而当板厚为60 cm时,3个时段减振值分别为92%、94%和88%。弹簧刚度为1.9 kN/mm时,减振值最大可达95%;弹簧刚度为7.0 kN/mm时,减振值最大为87%。
从图5中可看出,钢弹簧浮置板有着显著的隔振效果,但随长度增大,浮置板结构减振性能有降低的可能。4种厚度的浮置板中,厚度为30 cm的浮置板隔振效果相对较差,其他3种厚度的浮置板隔振效果较好。弹簧刚度为1.9 kN/mm的浮置板隔振效果最好,随着弹簧刚度的增大,浮置板隔振效果相对较差。
从表5也可知,随着支承间距的减小,结构的隔振效果越来越差。支承间距为3 m时,隔振减振值最大可以达到90%;而当支承间距为1.2 m时,隔振减振值仅为49%。结合图5(d)可以得出,支承间距较大的浮置板隔振性能相对较好。
对激振作用下浮置板的振动加速度时程进行傅里叶变换,将时域转换至频域。限于篇幅,仅列出浮置板厚度45 cm、弹簧钢度3.6 kN/mm、支承间距3.0 m(以下均同)时4种长度的钢弹簧浮置板在3个时段下的频谱曲线,如图6所示。
从图6可以看出,3个时段混合车流时浮置板主要振动频段位于3.0~40.0 Hz之间,这说明市政道路在交通荷载作用下以低频振动为主;频谱峰值对应的频率为18.0、14.5、14.5 Hz;在3.0~4.0 Hz和14.0~18.0 Hz范围处出现振动能量集中现象。从图6中还可以看出,晚高峰时段浮置板响应频谱曲线的峰值大于其他两个时段。
4.3VLz振级分析
振动加速度级VAL的定义为[14]:
式中:VAL为振动加速度级,单位dB;a为振动加速度有效值;a0为基准加速度10-6 m/s2。
VLz是按照ISO 26311 1985所规定的全身振动Z计权因子修正后得到的振动加速度级[15],1/3倍频程中心频率的最大加速度级记为分频最大振级,单位为dB。各样本在3个时段混合车流荷载激振下的1/3倍频程振动加速度级计算结果如表6所示。图7和图8分别为早、中、晚高峰时段振动加速度级和不同长度的浮置板1/3倍频程振动加速度级计算结果。
从表6中可看出,浮置板越厚,VLz振级越小,当厚度为30 cm时,早、中、晚3个时段的VLz振级分别为42.5、44.3、54.3 dB,而板厚为75 cm时,3个时段的振级为40.7、35.5、51.9 dB,分别为30 cm时的96%、80%和96%。随着弹簧刚度的增大,VLz振级不断增大,刚度从1.9 kN/mm增加到7.0 kN/mm时,3个时段VLz振级的峰值均增大了10 dB左右。不同支承间距下VLz振级的峰值变化十分明显,从表6可以得出,早、中、晚3个时段的VLz振级峰值随着支承间距的增大而减小,支承间距每增大0.6 m,VLz振级峰值减小5%~10%左右。
从图8中也可以看出,VLz振级在0~18 Hz范围内随频率增大而增大,之后随频率增大而降低,3个高峰车流时段,晚高峰振级最大,为52.9 dB。随着板长的增加,VLz振级略有增加,但未超过城市区域环境振动标准(GB 10070—1988)二类夜间标准72 dB[14]。
4.4插入损失
插入损失是描述振动系统中插入隔振措施后减振效果的物理量,定义为[15]
式中:I1为没有采用减隔振措施的响应;I2为采用减隔振措施后的响应。
采用先計权后求差的方法,先得到采用减隔振措施前、后两种情况的Z振级,然后,再对二者做差求得计权后的插入损失。当LIL大于0时,说明浮置板结构起到了减振效果,反之,当LIL小于0时,说明浮置板结构并未取得减振效果,反而放大了结构的振动。
表7和图9、图10分别为4种长度浮置板在3个交通高峰时段下插入损失小于0 dB的频段和插入损失曲线。从表7和图9、图10可以看出,插入损失小于0 dB的频段在0~5 Hz范围内,大于5 Hz频率范围插入损失均为正值,其中,午间时段插入损失的负值在2.5~5 Hz范围。不同厚度时插入损失小于0 dB的频段在0~8 Hz范围,随着浮置板厚度的增大,插入损失负值所在频段长度有所减小,这说明厚板较薄板的隔振性能好。弹簧刚度变化时插入损失小于0 dB的频段在0~8 Hz范围内,弹簧刚度较大时,振动频段更宽,频率高,减振性能较差。支承间距在1.8~3.0 m时,插入损失负值频率均小于10 Hz,但间距为1.2 m时,插入损失负值所在频段为12.5 Hz,说明支承间距较大的浮置板结构比支承间距小的浮置板结构减振性能好。
由频域分析可知,浮置板主要振动频段位于0~40 Hz之间,且以低频振动为主。表8为交通荷载激励下插入损失在0~40 Hz内的最大值。从表8可以看出,浮置板长度越长,插入损失越小,当长度为30 m时,插入损失可达34.2 dB,长度为120 m时,插入损失值为28.2 dB。同理,其他3个参数对浮置板隔振性能的影响也可以从插入损失在0~40 Hz范围内得到:其他参数相同条件下,厚度越大,浮置板隔振效果好;弹簧刚度越小,浮置板隔振效果越好;支撑间距越大,浮置板隔振效果越好。
5结论
在钢弹簧浮置板有限元模型试验验证的基础上,利用ANSYS有限元软件建立81个样本的有限元分析模型,进行了模态分析与实测交通荷载作用下的时域、频域、VLz振级和插入损失分析,对钢弹簧隔振器的浮置板道路设计参数进行了研究。研究表明:
1)随着浮置板长度的减小、厚度的增大、弹簧刚度的减小、支承间距的增大,浮置板结构的隔振效果得到了明显提高;对于0~40 Hz范围内的振动响应,所有样本中最大减振量为40.6 dB,基频处最大放大量为17.4 dB。
2)在本文的钢弹簧设置方式下,浮置板固有频率随着长度的增加而降低,且阶数越高,降低的幅度越大;浮置板第1阶固有频率随着厚度的增加逐渐递减,且降幅比较明显,但以后各阶固有频率反而增大,且阶数越高,增幅越大;浮置板固有频率随着弹簧刚度的增大而增大;浮置板自振频率随支承间距的减小而增加,且随着阶数的增高,其增幅越大。
3)各样本基频主要分布在4.0~10.0 Hz,基频直接影响钢弹簧浮置板在低频范围内的隔振性能。为了提高隔振效果,应尽可能降低钢弹簧浮置板的基频,可通过增大浮置板质量、降低钢弹簧刚度或增大弹簧间距来实现,但过大的质量将增大结构高度,过低的弹簧刚度或将造成结构的沉降和不稳定,因此应合理取值。
4)各个样本VLz振级在0~18 Hz范围内随频率增大而增大,之后随频率增大而降低,最大为52.9 dB。随着板长的增加,VLz振级略有增加,但未超过城市区域环境振动标准(GB 10070—1988)二类夜间72 dB限值标准。
5)交通荷载作用下,浮置板结构振动放大频段位于基频附近及14.0~18.0 Hz;从插入损失分析结果来看,起隔振作用的频段下限因浮置板参数而不同,但对10 Hz以上频段均能起到良好的隔振效果。参考文献:
[1] LOMBAERT G, DEGRANDE G, VANHAUWERE B, et al. The control of groundborne vibrations from railway traffic by means of continuous floating slabs [J]. Journal of Sound and Vibration, 2006, 297(3/4/5): 946961.
[2] HUI C K, NG C F. The effects of floating slab bending resonances on the vibration isolation of rail viaduct [J]. Applied Acoustics, 2009, 70(6): 830844.
[3] 李增光, 吴天行. 浮置板轨道二维建模及隔振性能分析[J]. 铁道学报, 2011, 33(8): 9398.
LI Z G, WU T X. 2D modelling of floating slab track and performance analysis on vibration isolation [J]. Journal of the China Railway Society, 2011, 33(8): 9398. (in Chinese)
[4] 刘维宁, 丁德云, 李克飞, 等. 钢弹簧浮置板轨道低频特征试验研究[J]. 土木工程学报, 2011, 44(8): 118125.
LIU W N, DING D Y, LI K F, et al. Experimental study of the lowfrequency vibration characteristics of steel spring floating slab track [J]. China Civil Engineering Journal, 2011, 44(8): 118125. (in Chinese)
[5] 韦红亮, 练松良, 周宇. 高架钢弹簧浮置板轨道减振特性分析[J]. 同济大学学报(自然科学版), 2012, 40(9): 13421348.
WEI H L, LIAN S L, ZHOU Y. Vibration reduction characteristics of steel spring floating slab track in metro viaduct [J]. Journal of Tongji University(Natural Science), 2012, 40(9): 13421348. (in Chinese)
[6] 王颖轶, 刘学文, 黄醒春. 短型浮置板轨道减振系统振动响应分析: 板下结构参数[J]. 上海交通大学学报, 2013, 47(10): 15521556.
WANG Y Y, LIU X W, HUANG X C. Vibration response analysis of the short floating slab track system: board structure parameters [J]. Journal of Shanghai Jiao Tong University, 2013, 47(10): 15521556. (in Chinese)
[7] 蒋吉清, 王永安, 魏纲, 等. 基于剪力铰的浮置板轨道减振性能优化分析[J]. 中国铁道科学, 2017, 38(4): 1523.
JIANG J Q, WANG Y A, WEI G, et al. Optimum analysis of vibration reduction performance for floating slab track based on shear hinge [J]. China Railway Science, 2017, 38(4): 1523. (in Chinese)
[8] 韦凯, 豆银玲, 杨麒陆, 等. 钢弹簧浮置板轨道的随机振动分析及参数优化[J]. 华中科技大学学报(自然科学版), 2017, 45(8): 115119.
WEI K, DOU Y L, YANG Q L, et al. Random vibration analysis and parameter optimization of steelspring floatingslab track [J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2017, 45(8): 115119. (in Chinese)
[9] 黃强, 黄宏伟, 张冬梅. 移动荷载作用下离散支承浮置板轨道振动响应研究[J]. 振动与冲击, 2018, 37(19): 190197.
HUANG Q, HUANG H W, ZHANG D M. Vibration response of discretely supported floating slab track under a moving load [J]. Journal of Vibration and Shock, 2018, 37(19): 190197. (in Chinese)
[10] 李林峰, 马蒙, 刘维宁, 等. 不同激励作用下钢弹簧浮置板轨道减振效果研究[J]. 工程力学, 2018, 35(Sup1): 253258.
LI L F, MA M, LIU W N, et al. Analysis for the vibration reduction characteristics of steel spring floating slab tracks under different types of excitation [J]. Engineering Mechanics, 2018, 35(Sup1): 253258. (in Chinese)
[11] 杨文茂, 辛涛, 周华龙, 等. U型梁上减振垫浮置板轨道系统动力分析[J]. 铁道工程学报, 2019, 36(2): 4448.
YANG W M, XIN T, ZHOU H L, et al. Dynamic analysis of damping mat floating track system on Ubeam [J]. Journal of Railway Engineering Society, 2019, 36(2): 4448. (in Chinese)
[12] 李小珍, 聂骏, 郭镇, 等. 钢弹簧浮置板轨道对箱梁振动声辐射的影响研究[J]. 振动与冲击, 2019, 38(13): 3441.
LI X Z, NIE J, GUO Z, et al. Effects of steel spring floating slab track on vibration and sound radiation of a boxgirder [J]. Journal of Vibration and Shock, 2019, 38(13): 3441. (in Chinese)
[13] 克拉夫, 彭津. 结构动力学[M]. 王光远, 译. 北京: 科學出版社, 1981.
CLOUGH R, PENZIEN J. Dynamics of structures[M]. WANG G Y, translated. Beijing: Science Press, 1981. (in Chinese)
[14] 城市区域环境振动标准: GB 10070—1988 [S]. 北京:中国标准出版社, 1988.
Standard of environmental vibration in urban area: GB 100701988 [S]. Beijing: Standards Press of China,1988. (in Chinese)
[15] 刘维宁, 马蒙. 地铁列车振动环境影响的预测、评估与控制[M]. 北京: 科学出版社, 2014.
LIU W N, MA M. Metro train induced environmental vibrations: Prediction, evaluation and control [M]. Beijing: Science Press, 2014. (in Chinese)
(编辑王秀玲)

