凯威特K8型网壳结构的稳定性能分析

黄宝仪 艾德生

（1.广西大学土木建筑工程学院， 广西 南宁 530004；2.上海众鑫建筑设计研究院， 上海 200083）

0 引言

近几十年来，随着经济技术的不断发展，各式各样的空间结构已大量运用到实际工程中，其中网壳结构由于具有自重轻、刚度大，造型富于变化等优点应用最为广泛[1,2]。网壳结构的历史可以追溯到19 世纪60年代，1863年，德国工程师施威德勒设计了第一座网壳结构[3,4]，此后，网壳结构便得到了广泛的应用。在对网壳结构的分析设计中，考虑的最重要的一个问题就是结构的稳定性[5]，同时，网壳结构属于缺陷敏感性结构，往往很小的缺陷就会大大降低结构的稳定承载力[6]。目前常见的球面网壳结构形式有：肋环型、凯威特型、施威德勒型等，本文以凯威特K8 型单层球面网壳结构为例，对其进行稳定性分析。

1 结构有限元模型

计算模型采用50m 跨度，矢跨比为1/6 的凯威特K8 型单层球面网壳结构。结构的杆件采用截面为Φ80*4 的Q235 圆钢管，弹性模量为E=2.06×105N/mm2，泊松比为0.3，在ANSYS 中采用BEAM188 单元来模拟实际杆件，并把截面定义为圆管截面，更贴近实际工程应用。计算时，将荷载全部转化为集中荷载并施加在节点上。

2 结构分析方法

2.1 特征值屈曲分析原理[7]

在对结构进行稳定性分析时，基于线弹性特征值屈曲响应分析，结构的屈曲临界荷载可表示为：

式中，P 为作用荷载； λi为第i 阶屈曲特征值。根据平衡状态下的势能原理，结构的特征值方程可表示为：

式中，［ KE］为结构总体弹性刚度矩阵；［ KG］为结构总体几何刚度矩阵；｛φi｝为与 λi对应的特征向量。在ANSYS 的特征值屈曲分析中，给出的结果是｛φi｝和 λi，即屈曲荷载系数和屈曲模态。

2.2 非线性分析原理

对于几何非线性问题而言，结构的平衡方程为[7,8]：

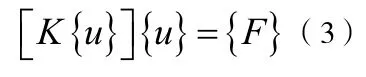
式中， ［K｛u ｝］为结构切线刚度矩阵；｛u｝ 为结构位移向量；｛F｝为结构荷载向量。求解非线性方程组一般采用Newton-Raphson 方法（简称NR 法），将平衡方程写成NR 法迭代公式为：

在ANSYS 的求解过程中，提供了完全NR 法、改进的NR 法和初始刚度法等选项，为了更好地跟踪到结构全过程平衡路径，ANSYS 在对非线性方程组求解的时候，通常采用牛顿-拉弗森法和弧长法相结合的策略。

3 结构的特征值屈曲分析

利用ANSYS 软件对结构进行特征值屈曲分析，提取出前五阶的屈曲特征值，具体数值如下表1 所示。

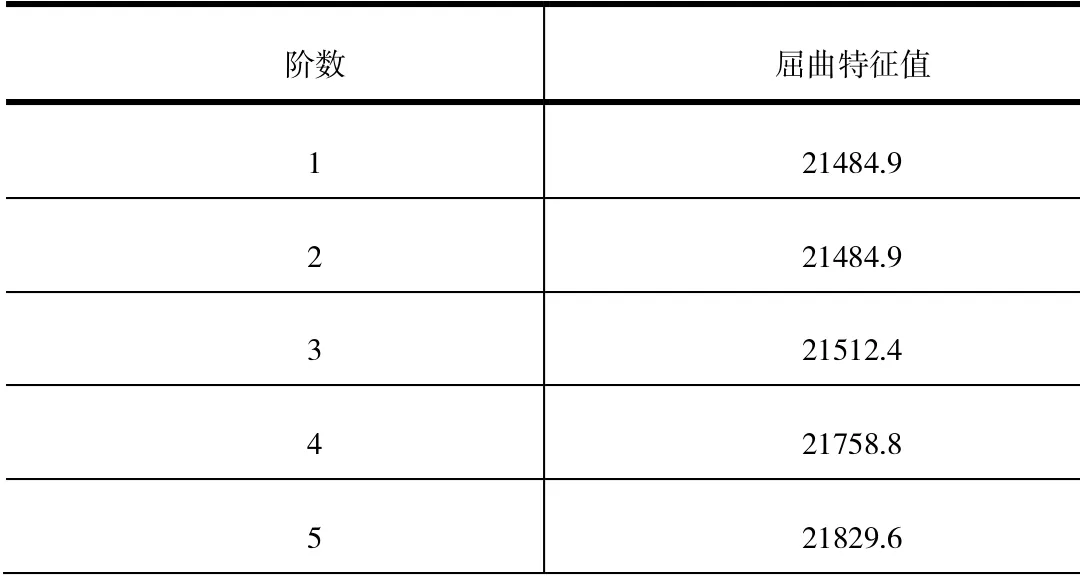
表1 结构前五阶屈曲特征值

由表1 中的数据可知，在前五阶范围内，结构的屈曲特征值随着阶数的增加而增大，第1、2 阶屈曲特征值相同，均为21484.9，是前五阶中的最小值，对应的屈曲临界荷载为21.485kN。

下面给出结构前五阶的特征值屈曲模态图形，见下图1。

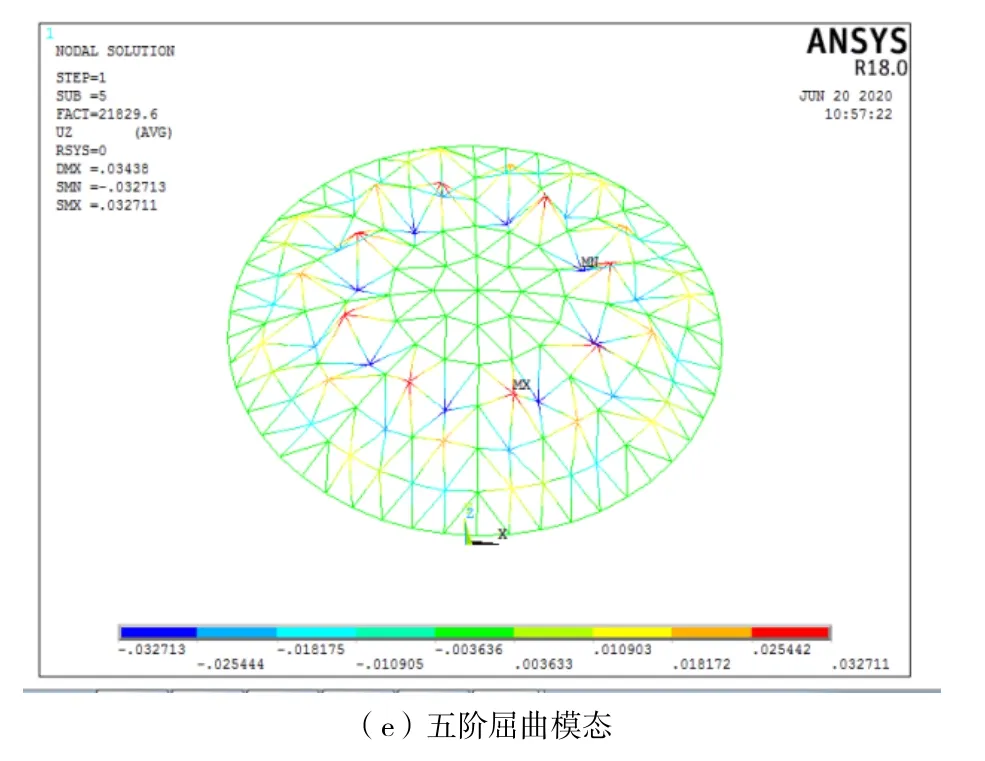
图1 结构前五阶特征值屈曲模态

由图1 可以看出，第1、2 阶屈曲模态主要表现为径向杆件发生屈曲，最大竖向位移出现在第二环，为0.080876m；第3 阶中，屈曲模态呈对称形式，环向杆件发生屈曲，最大竖向位移出现在第四环，为0.034228m；第4阶中，最大位移出现在中心节点位置，位移向上，位移值为0.334426m；第5阶中，斜杆发生屈曲，最大竖向位移出现在第三环，为0.03438m。从整体来看，结构的屈曲模态有一定的对称性，变形主要集中在顶点及顶点附近的环杆位置。

4 影响凯威特型球面网壳结构稳定性的因素

4.1 矢跨比

保持结构跨度为50 米，初始缺陷为L/500 不变，分析矢跨比在1/3～1/7之间的结构稳定性能。不同矢跨比情况下结构的荷载-位移曲线如下图所示。

图2 不同矢跨比下结构的荷载-位移曲线图

由上图可知，矢跨比为1/3，1/4，1/5，1/6，1/7 情况下，结构屈曲临界荷载分别为：27.7kN，22.9kN，6.59kN，8.93kN，9.82kN。从图中可以看出，当矢跨比为1/3 和1/4 时，在初始加载阶段，结构的荷载-位移曲线基本上呈线性关系迅速上升，结构整体刚度较大。随着矢跨比的减小，结构稳定承载力先降低后提高，当矢跨比从1/3 降到1/5 的时候，承载力呈不断减小的趋势，但当矢跨比从1/5 变化到1/7 的时候，承载力得到一定程度的提高。总的来说，减小矢跨比并不能提高结构的稳定承载力，在设计过程中不宜选取过小的矢跨比。

4.2 跨度

保持结构矢跨比为1/6，初始缺陷为L/500[9,10]不变，分析跨度在40m～100m之间的结构稳定性能。不同跨度情况下结构的荷载-位移曲线如下图所示。

图3 不同跨度下结构的荷载-位移曲线图

由上图可知，跨度为40m，50m，60m，80m，100m 情况下对应的屈曲临界荷载分别为：16.0kN，8.93kN，7.78kN，5.41kN，3.9kN。从图中可以看出，随着结构跨度的增大，网壳荷载-位移曲线在初始加载阶段的斜率逐渐变小，说明结构的刚度逐渐变小。随着跨度的增大，结构稳定承载力呈逐渐减小的趋势，说明增大跨度并不能提高结构的稳定承载力，在设计时不能一味地增大跨度，应结合适当的矢跨比来确定结构尺寸。

4.3 初始缺陷

保持结构跨度为50 米，矢跨比为1/6 不变，结构初始几何缺陷大小在L/300～L/2000 之间变化，分析初始缺陷大小对结构稳定性的影响。不同初始缺陷情况下结构的荷载-位移曲线如下图所示。

图4 不同初始缺陷下结构的荷载-位移曲线图

由上图可知，初始缺陷为L/300，L/500，L/700，L/1000，L/2000 情况下对应的屈曲临界荷载分别为：8.97kN，8.93kN，9.45kN，13.5kN，18.0kN。计算结果表明，结构对初始缺陷较为敏感，随着初始几何缺陷的增大，网壳前半段的斜率逐渐变小，即结构的刚度逐渐减小；随初始几何缺陷的增大，结构刚度减小的速度也越快，说明初始几何缺陷的大小会不同程度地降低结构的稳定承载力。因此，在实际设计中，应适当考虑结构的初始几何缺陷，选择合适的缺陷值。

5 结论

本文主要研究了凯威特K8 型单层球面网壳结构的稳定性能，并得出如下结论：

（1）通过对结构进行特征值屈曲分析发现结构的屈曲模态有一定的对称性，且变形集中在顶点及顶点附近的环杆位置。

（2）结构的矢跨比在一定范围内增大，可以有效地提高结构的稳定承载力。

（3）随着结构跨度的不断增大，网壳结构的稳定承载力会降低，设计过程中不能一味地追求跨度的增大，应结合矢跨比的影响，寻找适合的结构尺寸。

（4）凯威特K8 型单层网壳结构属于缺陷敏感性结构，初始缺陷的存在会在一定程度上降低结构的稳定承载力，实际工程设计中，应结合实际情况，采取合适的初始缺陷大小。