基于E-CARGO模型的云制造服务组合方法
钱 晨,张以文,吴其林,胡 博
1(安徽大学 计算机科学与技术学院,合肥 230601)2(巢湖学院 信息工程学院,合肥 238000)3(深圳易伙科技有限责任公司,深圳 518055)
E-mail :zywahu@qq.com
1 引 言
近年来,为满足客户的多元化需求,力争在国际市场上立足,全球制造业积极进行转型发展.世界各地相关学者的研究方向和企业生产发展的重点均转向智能化、个性化、服务化、敏捷化和协作化.在此背景下,出现了许多新的技术和理念来改善制造业生态,云制造概念随之产生.
云制造是一种利用网络和云制造服务平台,按用户需求组织网上制造资源,为用户提供各类按需制造服务的一种网络化制造新模式[1].云制造借鉴云计算的思想[2],利用服务计算和制造技术,将制造资源和制造能力转化为制造服务,实现制造资源和制造能力的智能统一管理和运营,实现制造资源和制造能力的充分共享和流通[3].云制造系统是由云制造服务请求者、云制造服务提供者和云制造服务平台组成.服务提供者将闲置的硬件资源(如设备资源、计算资源、物料资源等)或软件资源(如应用软件资源、技术和知识资源、数据和信息资源等)提交至云平台,然后由云平台将这些闲置资源进行网络虚拟化并进一步封装后发布到云制造平台上.当服务请求者向云平台提交任务需求时,任务被分解成不可再分的子任务,并对这些子任务在云平台上进行搜索匹配,给出满足任务需求的服务组合,然后由一个或多个服务提供者完成服务请求者提交的任务.
由于协同性是云制造的典型特征,通过多个服务之间的协作实现协同完成制造任务;且云制造服务组合方案具有明显的动态性、不确定性等特点[4].因此,本文从基于角色的协同[5](Role-Based Collaboration,RBC)的角度研究云制造服务组合问题并对其建模.本文的主要贡献如下:
1)基于E-CARGO模型对云制造服务组合问题进行建模,提出一种基于角色的协同云制造服务组合优化方法.该方法建立了服务组合问题和E-CARGO模型间的映射关系,构建了基于角色的协同云制造服务组合模型.
2)针对云制造服务历史QoS的不确定性,引入云模型理论对动态QoS进行分析,并计算QoS云模型的相似度,进而得到资格评估矩阵,然后对基于角色的协同云制造服务组合问题进行求解,得到最优云制造服务组合方案.
2 相关工作
2.1 云制造服务组合
随着网络化协同制造模式的发展,制造服务的数量不断增长,云制造服务系统将会出现严重的信息过载.云制造服务平台为服务请求者在大量的制造资源中选择合适的服务进行服务组合遇到了很大的困难[6],在此背景下云制造服务组合问题得到了广泛的关注.高新勤等[7]为了实现服务供给与服务请求的快速匹配,提出了基于相似度的加工设备云服务聚类方法;简琤峰等[8]提出一种基于ONBA并结合二阶振荡和差分进化算法的改进算法,利用改进算法获取云制造模型的调度数据,并通过该调度数据对IDBN深度学习模型进行训练;管力明等[9]提出一种基于综合信誉度的云制造服务组合算法,算法从用户对时间、成本和质量等属性的重视度和期望值综合得出服务组合的信誉度,通过调整属性权重值达到多目标优化的目的.此外,基于语义的服务组合[10]、面向多任务的服务组合[11]、基于服务质量的服务组合[12,13]等方法也被提出.同时,智能算法也被广泛的用于云制造服务组合中,如人工蜂群算法[14]、粒子群算法[15,16]等.如今,国内外对云制造服务组合问题的研究已经取得很大进展,但很少有方法能够考虑到云制造的协同性.本文从RBC的角度研究云制造服务组合问题,提出一种基于角色的协同云制造服务组合优化方法.
2.2 基于角色的协同(RBC)
在协作系统中,RBC是一种新兴的计算方法学,它以角色为核心机制,描述并支持解决协同问题.E-CARGO模型是RBC中最重要的模型,以六元组(环境、类、代理、角色、组、对象)的形式清晰的描述了RBC系统[17].E-CARGO模型的研究成果为群组角色分配问题[18](Group Role Assignment,GRA)、冲突代理的GRA问题[19](GRA With Conflict Agents,GRACA)、群组多角色分配问题[20](Group Multi-Role Assignment,GMRA)等提供了理论模型及解决方案.最近,E-CARGO模型已经被成功应用到混合云中数据密集型应用的服务组合中[21].协同性是云制造的典型特征,为清晰的描述云制造的协同性问题,本文首次将E-CARGO模型应用到云制造场景中.
3 云制造服务组合
3.1 问题描述
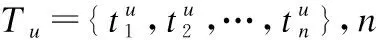
3.2 E-CARGO建模
2006年朱海滨教授提出E-CARGO模型,并采用此模型刻画和描述了一个协作系统.E-CARGO模型采用9元组形式化描述一个RBC系统.一个协作系统∑由9个元组构成:
∑::=
(1)
其中,C,O,A,M,R,E,G,s0,H分别代表协作系统中的类(Class)、对象(Object)、代理(Agent)、消息(Message)、角色(Role)、环境(Environment)、组(Group)、协作系统的初始状态s0和用户(User)的有限集.
协作系统中应用E-CARGO模型主要关注的元素为E,C,O,R,A,G.在本文中E表示为问题的环境,即一组制造服务的计划和建议.C是一组表示与E相关的抽象概念定义的类.O是一组和C相关的具体对象.R是云制造中属于同一类型子任务的集合.A是云制造中同一类型子任务的服务候选集.G是一个组,为了获得最优的组,需要将合适的服务分配给合适的任务.
如图1 所示,子任务、服务和角色、代理的映射关系如下:
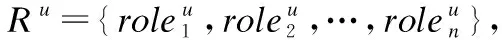

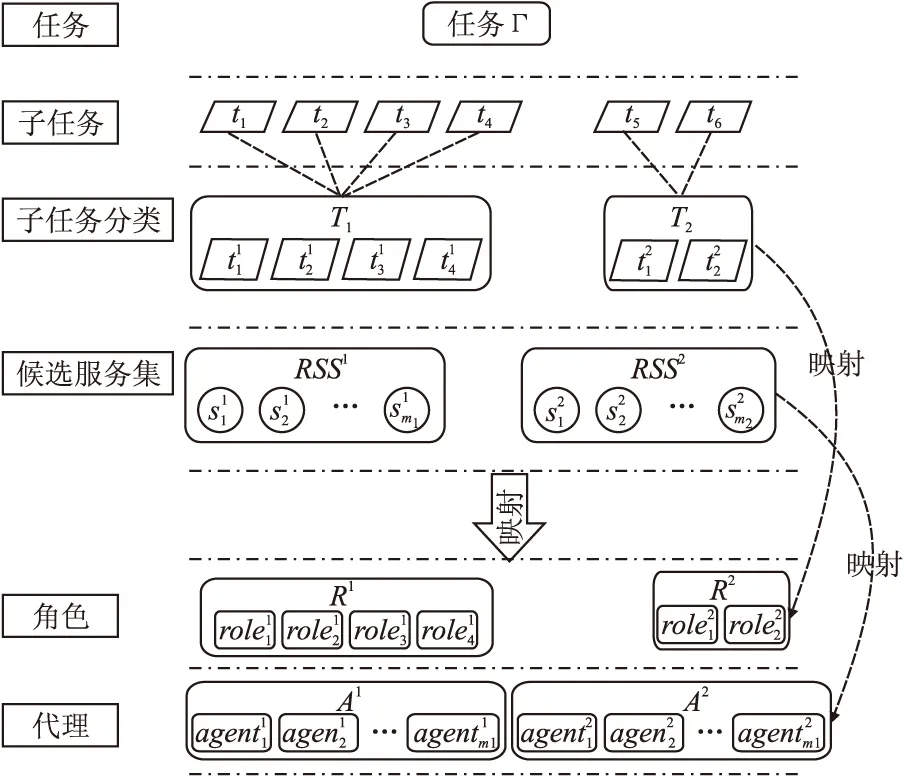
图1 云制造服务组合和E-CARGO模型的映射关系Fig.1 Mapping the cloud manufacturing service composition and the E-CARGO model
文中,Ru、Au对应了一个E-CARGO模型,即每种类型的子任务集合都建立一个E-CARGO模型,以Tu类型的子任务为例,运用E-CARGO模型还需要定义如下4个参数:
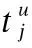
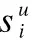
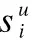
4)组评估值ρ,表示在满足约束条件的情况下,一个组中被分配的服务的资格评估值之和.
基于以上分析,目标函数定义为:
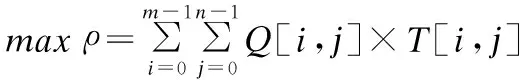
(2)
s.t.
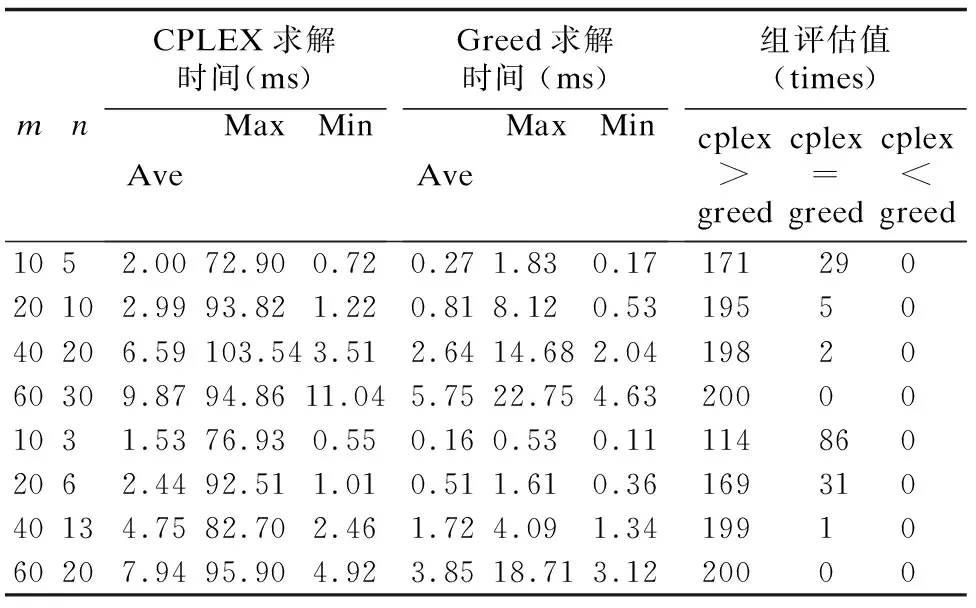
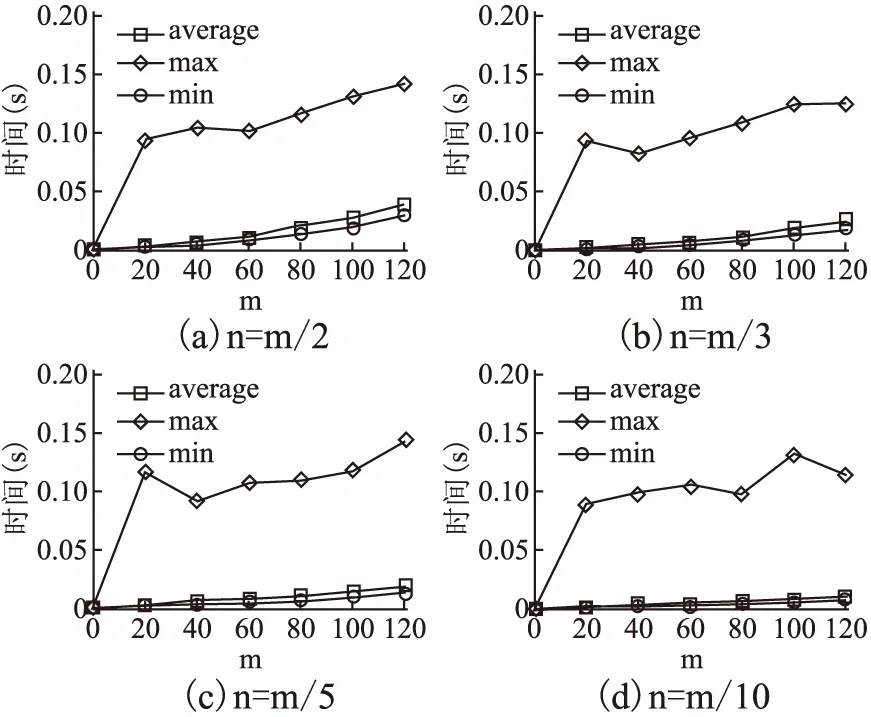
T[i,j]∈{0,1}(0≤i (3) (4) (5) 式(3)表示服务只有被分配和不分配两种选择;式(4)表示该问题必须满足子任务需求向量L的约束,即规定子任务需要多少个服务来协同完成;式(5)表示一个服务只能被分配给一个子任务. (6) 根据式(6),候选服务集RSSu中m个服务对n个Tu类型子任务的QoS云模型矩阵可表示为: (7) 由于服务状态和能力的多样化,即使相同的任务被执行多次,每次的QoS也不会完全相同.因此,一个好的服务应当提供稳定的QoS,即多次完成同一任务得到相同或相近的QoS.En和He的值越小,QoS越稳定.由此,我们定义了理想解,在最好情况下的cm为: (8) 同理,最坏情况下的cm为: (9) 为了给任务选择合适的服务,通过计算QoS云模型之间的相似度来识别服务QoS之间的差异是至关重要的.这里我们采用欧式距离来计算相似度.欧式距离的公式如下: (10) (11) 3.4.1 方法流程 根据以上分析,基于角色的协同云制造服务组合优化方法流程如下: 1)用户提交任务Γ,任务Γ被分解为子任务,再按照子任务的类型组合,属于同一种类型的子任务构成任务类型集合; 2)每种任务类型集合对应一个候选服务集,每个服务只能完成一个子任务,一个子任务可能需要多个服务协同完成; 3)每种任务类型及对应的候选服务集构建一个E-CARGO模型,子任务、服务与E-CARGO模型中的角色、代理构建了映射关系; 4)以Tu类型子任务及对应的候选服务集RSSu为例,进行下述步骤计算,其他任务类型进行相同计算; 9)求解在满足约束3)、4)、5)条件下的目标函数式(2); 10)解出分配矩阵T,得到最优服务组合方案. 3.4.2 方法求解 使用CPLEX求解目标函数包含如下两个步骤: 1)确定CPLEX需要的目标函数系数、约束系数、右侧约束值和上下界.本文使用Q,L,T定义CPLEX中的线性规划问题.Q是目标函数的系数,T是变量,它的上下界是1和0; 2)添加目标函数和约束的表达式.云制造服务组合问题的目标函数可以用Q和T的一维数组形式描述. 伪代码如下所示. 求解算法: 输入:Qualification matrixQand Lower bound vectorL 输出:Group performanceρand assignment matrixT Begin 1. Initialize an IloCplex object; 2. Initialize assignment one-dimensional arrayX; 3. transform matrixQinto one-dimensional arrayQT; 4. add the optimization objective Equation(2); 5. add the constraint Equation(4); 6. add the constraint Equation(5); 7. Invoke the solve() method of CPLEX; End 第1行,创建IloCplex对象,IloCplex类是用来创建和求解多种数学编程模型的类.第2行,初始化分配矩阵T,调用IloCplex对象的方法intVarArray(m*n,0,1)返回一维数组X,方法中的第一个参数是以一维数组X的形式表示了分配矩阵T,第二个和第三个参数定义了数组中每个变量的范围.第3行,Q矩阵用一维数组QT表示.第4行,使用IloCplex对象的方法addMaximize(IloCplex.scalProd(X,QT))创建目标函数.第5、6行是为CPLEX添加约束:①调用IloCplex对象的方法linearNumExpr()声明表达式对象,并返回IloLinearNumExpr对象;②通过调用方法将所有项添加到对象IloLinearNumExpr中;③调用IloCplex对象的方法(addEq(IloLinearNumExpr))或addLe(IloLinearNumExpr))将约束表达式添加到CPLEX中.第7行,调用IloCplex对象的方法solve()求解该问题. 开发平台为Eclipse,编程语言为Java,机器配置为core i7-49703处理器,16G内存,windows 10操作系统. 表1 服务的QoS历史记录Table 1 QoS history of service 根据式(6)可计算出服务对各子任务的三个云数字特征,如表2所示. 表2 服务的云数字特征Table 2 Cloud digital characteristics of services 根据式(8)、式(9)计算出理想情况下的云数字特征cm+={0.82,0,0}、cm-={0,0.30,0.15}.再由式(11)计算出服务对各子任务的胜任程度. 表3 服务的值Table value of the service 如表3所示,将表3作为资格评估矩阵Q,根据E-CARGO模型,L=[1,1,2,1],由式(2)、式(3)、式(4)、式(5),利用IBM ILOG CPLEX工具包可计算出分配矩阵T: 为了验证所提出方法的性能,我们将所提出的方法与贪心算法作比较.每给定一个m和n的值,均重复实验200次,每一次实验Q和L都随机更新.为了比较n/m的比值对性能的影响,我们组成两组测试,比值分别为1/2和1/3.分别记录当m和n取不同值时求解服务组合问题的平均时间、最大时间和最小时间.同时还列出了CPLEX得到的组评估值比贪心算法得到的组评估值大的次数. 表4 CPLEX与贪心算法的比较Table 4 Comparison of CPLEX and greedy algorithm 由表4可以看出,本文方法的性能与m和n的大小有明显的关系.m和n的值越小,方法求解所需要的时间越少.例如,当m=10,n=5时,平均运行时间是2.00ms,而当m=60,n=30时,平均运行时间是9.87ms.由于贪心算法只考虑了每一步中的最好情况,在运行时间上自然更短,但是容易陷入局部最优.由实验可以看出,贪心算法得出的组的最大评估值往往不是最优的.当m的值较小时,贪心算法有一定的几率得到最优解,例如,当m=10,n=5,贪心算法在200次的实验中有29次和使用CPLEX求解一样达到了最优解.不过随着m的增大,贪心算法几乎不会达到最优解,只是近似最优解. m和n是解决问题复杂度的重要参数,对本文方法性能的影响重大.因此下面的实验我们研究改变m和n的值对本文方法性能的影响.m的范围从20到120,步长20,n/m比值分别为1/2、1/3、1/5和1/10,同一组m和n的值均运行200次.实验结果如图2所示. 图2 性能分析Fig.2 Analysis of performance 由实验结果可以看出,m和n的值越大,求解花费的时间越多.在m相同的情况下,n的值越小,求解时间越短.最大求解时间对应了给定m和n的值,200次重复实验中的一组特定数据,随着m和n的增长,最大求解时间呈波动增长.最大求解时间曲线的波动和下降意味着,求解一个较大规模的服务组合问题可能比求解较小规模服务组合问题花费的时间更少.最小求解时间随着m和n的增长而增长,最小求解时间和平均求解时间曲线是近似的,说明除了特定数据,大部分数据求解时间都是近似最小求解时间的.实验证明了本文提出方法的有效性,当问题规模增大到m=120,n=60时,最大求解时间是0.142s,最小求解时间是0.03s,平均求解时间是0.038s. 考虑到协同性作为云制造的典型特征,本文基于E-CARGO模型对云制造服务组合问题进行建模,提出一种基于角色的协同云制造服务组合优化方法.首先确立了服务组合问题和E-CARGO模型间的映射关系;其次将服务的不确定QoS转换为云模型的数字特征,通过相似度计算得到资格评估矩阵;最后解出最优服务组合方案.在接下来的研究工作中,我们将考虑服务间的约束关系,解决在复杂约束条件下的云制造服务组合问题.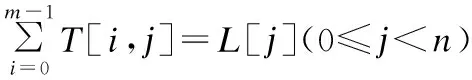
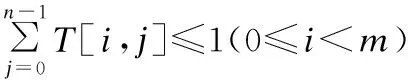
3.3 资格评估矩阵


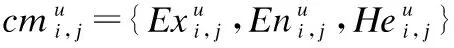
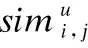
3.4 基于角色的协同云制造服务组合优化方法求解
4 实 验
4.1 实验环境
4.2 实 例
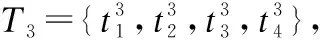
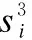
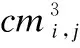
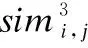
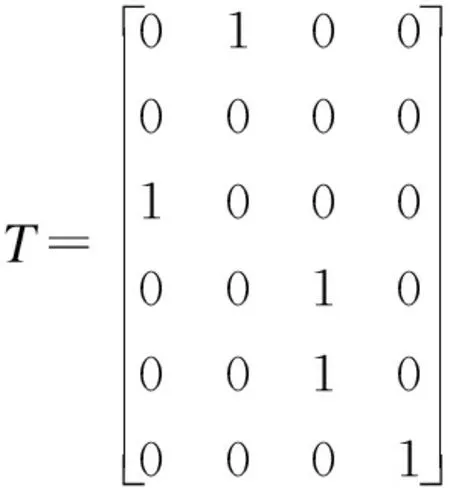
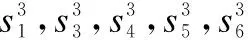
4.3 实验分析
5 总 结

