走廊层面交通小区划分方法的优化

宋俪婧，朱家正，刘雪杰，陈 静，缐 凯

(1.北京工业大学北京市交通工程重点实验室，北京100124；2.北京交通发展研究院，北京100073)

0 引 言

划分交通小区是交通预测和分析中的基础工作，国内外关于交通小区划分的研究很多.文献[1]提出交通小区双层划分概念和加权模糊聚类方法，并以海峡西岸经济区为例进行实例验证.该研究提出的分层概念和聚类方法对本研究具有重要的启示，但研究区域非公交走廊，聚类指标仍采用传统的社会经济和交通量数据；文献[2]提出了改进的K-means聚类方法在城市轨道交通事件量化分级中的应用；文献[3-5]分别应用不同聚类方法对交通小区进行划分；文献[6]应用移动网络数据对交通小区进行划分；文献[7]提出K-means 动态交通小区划分，并应用于公交服务水平评价.这些研究大多针对某一区域，聚类结果主要应用于全交通方式需求预测和分析中.聚类方法多采用模糊聚类和K-means.聚类指标多采用社会经济数据.

随着优先发展公交工作的不断深入，公交需求预测和出行特征分析很多都依赖于交通小区进行，而目前基于客运走廊层面的小区划分仍然缺少理论基础和实践经验.传统的依据人口、用地等指标聚类划分交通小区的方法常用于全方式交通规划中，在更为真实反应公交实际出行需求方面有待提升.随着大数据技术的不断发展，公交实际出行大数据可以更真实地反应公交乘客实际出行特征和需求.因此，本研究基于公交乘客出行特征选取划分指标，研究公交客运走廊交通小区划分的理论和方法，划分结果作为公交客运走廊交通需求预测和出行特征分析的基本单元.

1 公交客运走廊交通小区分层次划分理论

公交客运走廊是指在某一地域内，连接主要客流产生点和吸引点，有一定流向，有大运量的快速公共交通方式，有公交专用道等路权及设施保障的乘客运输的骨干线路.公交客运走廊有一定的影响区.通常在公交客运走廊线网优化等工作中，需要基于交通小区对走廊影响区内部产生吸引量以及内外交换量进行分析，因此需要研究走廊影响区内外的交通小区划分方法.

分层次的交通小区划分理论，如图1所示，将公交走廊分为直接影响区和间接影响区，并依据不同区域的不同需求对交通小区进行划分.由于公交走廊具有明显的通道性，其周边一定范围内是走廊客流的主要产生吸引地，称为走廊直接影响区，是需求分析的重点区域，应对区域内部交通小区进行细分.本研究基于公交IC卡数据获得的出行链数据，提取直接影响区内部出行量及起讫点，将起讫点作为聚类指标，通过引入聚类因子确定小区划分个数，选取聚类中心，对传统K-means聚类方法进行改进，有效克服传统方法随机选取聚类中心影响划分精度问题.在此基础上，依据公交站点等基础设施调整走廊边界，有效解决交通小区与公交站点的对应问题.走廊间接影响区主要用来分析和预测直接影响区与外围主要客流吸引点的交换量，不需要像直接影响内交通小区划分那样精细，只需预测主要交换量和空间分布即可，因此，本研究在北京市既有交通小区的基础上(针对多方式划分的交通小区)，对走廊间接影响区内既有交通小区进行合并处理.指标主要考虑人口、用地等因素，合并方法采用可充分考虑既有小区间的相似性和空间临接性的两维图论方法，使小区合并更接近实际.依据合并结果，仍以公交站点等基础设施对划分小区边界进行微调修正，以保证需求预测和分析结果更符合实际情况.

图1 交通小区分层次划分理论体系图Fig.1 Theoretical system of hierarchical TAZ division

2 公交客运走廊交通小区分层次划分方法

交通走廊小区划分方法包含直接影响区内小区细分和间接影响区小区合并两部分.

2.1 基于改进K-means聚类的走廊直接影响区内交通小区细化方法

K-means聚类算法是一种基于中心的常用聚类方法，每一类都有一个聚类中心，通过不断迭代，达到最优聚类结果，最终输出训练模型.K-means算法在实际应用中存在局限：一是受无法事先确定聚类个数影响聚类精度，二是随机选取初始聚类中心导致聚类结果不同.本研究通过引入聚类因子在聚类前确定小区划分个数，并初步选取聚类中心，有效克服了传统K-means聚类随机选取聚类中心影响划分精度的问题.

(1)引入聚类因子初步确定交通小区的个数及中心.

公交IC卡获得的出行起讫点数据能更精确的反映公交乘客出行特征，本研究综合考虑区内出行量，区内及区间距离等因素，定义聚类因子I初步确定交通小区的个数.聚类因子为各小区交通的相似性Din与各小区交通的差异性Dout的比值，即

式中：Din为各交通小区半径按出行量的加权平均值，代表各小区交通的相似性；Dout为各交通小区两两中心的距离之和，代表各小区间交通的差异性.

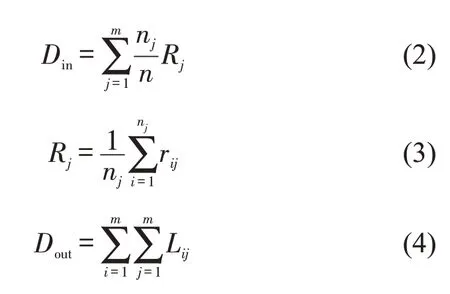
式中：nj为第j个交通小区内起讫点的个数；n为全部起讫点的个数；m为划分的交通小区个数；Rj为第j个交通小区的平均半径；rij为样本i到小区j中心的距离；Lij为小区i中心到小区j中心的欧式距离(由于经纬度坐标对欧式距离的贡献相同，且用不同小区中心间的直线距离表示其差异性最为直观，算法相对简单，因此选用欧式距离).

基于聚类因子I确定交通小区个数：同一小区内Din越小，表示交通特征相似性越强；不同小区间Dout越大，表示交通特征差异性越强.在确定小区个数时选择最小的聚类因子对应的交通小区个数.

具体步骤如下：

Step 1随机初始化起讫点的隶属度矩阵U，约束条件为

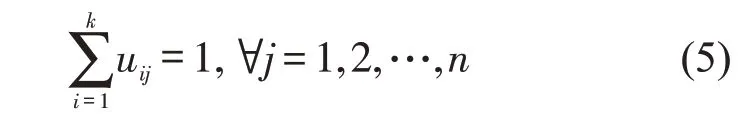
式中：uij为隶属度，表示样本j归属于小区i的隶属度.

Step 2通过隶属度矩阵、各起讫点间距离，引入拉格朗日乘数，在式(5)约束条件下，求导计算获得小区中心的经纬度为

式中：cix为小区中心的经度值；ciy为小区中心的纬度值；uij为隶属度；xj为第j个样本数据的经度值；yj为第j个样本数据的纬度值.

Step 3基于式(2)～式(4)计算Din和Dout，从而计算I.

Step 4确定交通小区个数的待选范围，得到聚类因子与小区个数对应关系图，确定小区个数.

Step 5确定小区个数后，将该个数对应下的小区中心位置作为精确划分的初始中心.

(2)基于K-means聚类精确划分交通小区.

在2.1节(1)初步确定小区个数后，会产生各小区交界处出现重叠的聚类结果问题，K-means聚类可有效克服该问题，因此通过K-means聚类对直接影响区内部交通小区进行细分，具体步骤如下：

Step 1基于2.1节(1)结果，将其获得的隶属度矩阵作为精确划分的隶属度uij，应用其初步划分的小区中心计算样本和簇中心的距离，并取为欧式距离，即

式中：uij为隶属度；xj为第j个样本的经度值；ci为第i个小区中心的经度值；m为划分的交通小区个数.

Step 2采用最大期望算法，在聚类因子的约束条件下进行迭代，迭代函数如式(8)所示.如果迭代函数相比上一次运算的结果改变不大，则终止迭代，此次迭代后uij非0 即1，有效克服了过程(1)中各小区聚类边界重叠的问题.

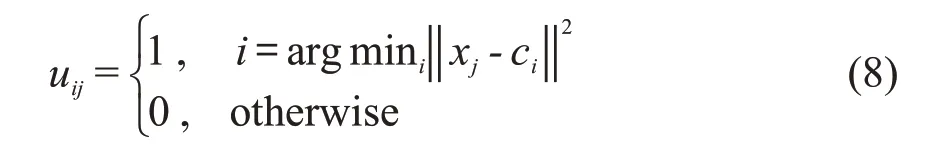
式中：uij为隶属度；xj为第j个样本数据；ci表示第i个小区中心位置.

Step 3聚类完成后，得到所有起讫点在各聚类小区中的分布，基于ArcGIS平台生成小区边界，并基于公交站点布局、结合各小区周边道路、用地等情况对生成的小区边界进行调整，形成聚类结果精细划分的小区边界.

2.2 走廊间接影响区交通小区合并方法

由于外围小区主要用于体现走廊与外部主要客流吸引点间的交换量，因此聚类指标重点考虑主要影响交换量的用地性质、人口数量等因素，同时还要考虑原有小区之间的相似性和空间连接性.因此本研究采用可体现空间连接性的两维图论聚类算法，主要步骤如下：

Step 1获取需合并小区i的指标向量xi={xi1,xi2,…,xim}，n个交通小区构成原始数据矩阵[xij]n⋅m.

Step 2将不同指标去除数据单位，转化为无量纲值，标准化公式为

式中：xij为小区i的第j项指标值.

Step 3构建位置关系无向加权图，计算连接边的权值，即相似系数.小区i和小区j之间的相似性系数为

式中：xik为小区i的第k项指标值；xjk为小区j的第k项指标值.

Step 4应用两维图论聚类算法选择不同阈值进行小区合并，并用F检验法确定最佳阈值，从而确定小区合并个数和布局.F统计量为

F统计量服从自由度为s-1、n-s的F分布，由式(11)可知，在一定的显著性水平下，通过显著性检验且F值越大，说明聚类效果最好.

Step 5基于ArcGIS 平台，根据各合并小区周边的公交站点、道路和重要分割线等情况对小区生成的边界进行微调，形成最终合并小区.

3 实例分析

3.1 数据来源

本研究采用北京市2018年5月的地面公交和轨道交通IC卡数据，共3.16亿条记录.剔除异常记录，剩余3.15亿条有效数据，对应约6.4亿个起讫点.基于交通调查中的统计数据获取2006个初始小区的人口和就业等数据.

3.2 广渠路客运走廊直接影响范围的确定

广渠路走廊自广渠门桥至宋梁路，26 km，是北京市中心城连接副中心的一条重要走廊，地铁1条，地面公交39条.由IC卡获得的公交乘客出行起讫点(如图2所示)可知，公交乘客出行起讫点主要分布在广渠路两侧5 km 范围内，因此本研究将广渠路走廊的直接影响区确定为道路两侧5 km范围.

图2 主要出行起讫点Fig.2 Main OD

3.3 广渠路客运走廊交通小区的划分

(1)直接影响区内部交通小区的细分.

基于公交IC卡获得的乘客出行链数据可得到直接影响区内所有起讫点位置数据，通过地理信息系统获得各起讫点间距离，初步确定走廊直接影响区内交通小区个数的待选范围[40，110]，得到聚类因子与交通小区个数对应关系如图3所示.

在40个小区的情况下，聚类因子相对较大；随着交通小区个数增加，聚类因子呈下降趋势，当小区个数增至70个时，聚类因子取到极小值；继续增加小区个数，聚类因子无明显变化，略有增大.因此，初步确定走廊直接影响区小区个数为70个.初步划分的各交通小区中心如表1所示.

图3 聚类因子与小区个数对应关系Fig.3 Cluster factors and number of TAZs

表1 初步划分小区中心位置Table1 Preliminary division of position of zone center through fuzzy C-means clustering

选定小区个数为70，将初始小区位置作为K-means聚类的初始化参数.通过走廊内公交起讫点确定隶属度矩阵，根据公交起讫点与各簇中心距离确定欧式距离，通过K-means聚类方法进行小区细分，结果如图4所示，图中每个点表示一个出行起讫点.

图4 百子湾路—高碑店路—王四营北路—东四环路区域聚类结果Fig.4 Regional clustering results

(2)间接影响区交通小区的合并.

以直接影响区南部交通小区为例，根据统计和交通调查数据，获得各小区人口、各类用地数据，形成聚类指标表.对指标进行标准化处理后，计算相似性矩阵，将相似性矩阵转换成权值.依据各小区拓扑关系，建立支撑树结构.依据权值获取相应阈值，顺序为：0.001、0.003、0.006、0.007、0.009，形成不同的最小支撑数.从图5可知，被合并小区的相似性程度随阈值增大而增大，被合并的小区类数逐渐减小，被合并的小区增加.当阈值取0.009时，所有的小区被合并成一个，显然与实际不相符.由小区拓扑关系和经验判断，当阈值大于等于0.007时，被合并的小区过大，也与实际不相符.因此，初步排除阈值取0.009和0.007两种情况.在显著性水平0.05的水平下，通过F检验确定最佳阈值，其中阈值为0.001时，F值为11.005，临界值为3.106；阈值为0.003时，F值为7.283，临界值为3.197；阈值为0.006时，F值为6.375，临界值为4.103.F值越大，说明不同类对象之间的差异越大，同类对象之间的差异越小，因此应选取F值最大对应的阈值，即最佳阈值为0.001，19个小区被合并为8个，如图6所示.

3.4 小区划分结果

依据上述方法，对广渠路走廊直接影响区内小区进行细化，细化后共70个交通小区.在北京市2 006个小区的基础上，对走廊外围小区进行合并，合并前后的小区对比如图7所示，其中图7(b)为细化和合并后的小区结果.

图5 不同阈值下聚类结果Fig.5 Clustering results

图6 合并小区示例Fig.6 Illustration of merging old TAZs to new TAZs within indirect influencing area

图7 广渠路走廊影响区域交通小区划分前后的对比图Fig.7 Comparison chart of TAZs clustering results

3.5 划分方法验证

利用DBI聚类性能评价指标判断改进方法的聚类效果，如式(13)所示，DDB越小表示聚类效果越好.结果如表2所示，说明本研究划分的交通小区更适用于公交客运走廊的出行特征分析和需求预测.

式中：为小区i的内部平均欧式距离；为小区j的内部平均欧式距离为小区i与小区j间的欧式距离；m为划分的小区个数.

表2 划分方法验证Table2 Verification of division methods

4 结 论

本研究基于公交出行大数据确定走廊直接影响区范围，提出客运交通走廊交通小区分层次划分理论以及公交客运走廊直接影响区和间接影响区交通小区划分方法.其中直接影响区内通过引入聚类因子，应用改进的K-means聚类方法，有效避免了K-means 需要制定初始聚类参数而影响聚类精度的问题.依据走廊间接影响区的特征提出的两维图论聚类法，充分考虑了交通小区合并的相似性和空间邻接性.经实例验证，该方法聚类结果较传统方法邻接性更优，且符合实际应用.本研究提出的公交客运走廊分层次交通小区划分方法是可行的，经DBI聚类性能评价指标分析，相比传统交通小区划分方法验证指标值更小，说明在走廊直接影响区内各小区间相似性更大，外部各小区间差异性更大，因此特征分析和需求预测结果将更加准确，且分层次的划分方法更适用于客运走廊层面分析公交运行特征和需求预测.应用该方法划分的交通小区可以为走廊公交线网优化、公交专用道运行效率评价等工作提供基本分析单元.