基于PSO-RVM模型的大坝安全监控研究
宋培玉 ,杨浩东 ,王嘉华
(1. 中煤科工集团南京设计研究院有限公司,江苏 南京 210019;
2. 江苏南水科技有限公司,江苏 南京 210012;
3. 河海大学理学院,江苏 南京 210098)
0 引言
利用实测数据建立监控模型是实现大坝工程安全预警的有效途径[1],目前逐步回归法、时间序列法、灰色系统理论等一系列传统的统计模型已经被应用到大坝安全监控中。朱劭宇等[2]利用马尔科夫链适应大波动的特点,将逐步回归和马尔科夫模型相结合并应用于大坝变形监测。针对多重共线性问题,姚远等[3]建立了偏最小二乘回归法的逐步回归模型,但模型系数难以解释。陈宏玉[4]在偏最小二乘法的基础上引入了半参数模型,有效地分离出观测数据中的系统误差,但模型处理过程较复杂。为避免灰色模型在长期预测的有效性受系统时间序列长短及数据变化的影响,魏迎奇等[5]建立等维 GM(1,1)动态预测模型对大坝变形进行了预测。针对大坝安全监控中数据的随机扰动误差影响,苏观南等[6]利用卡尔曼滤波消除原始数据扰动误差,再对大坝变形进行灰色预测。李萌等[7]利用灰色模型预测分形维数,建立了改进的大坝分形几何监控模型。针对大坝监测中常出现的非等间距数据,付浩雁等[8]通过引进指数平滑法构建了改进的非等间距灰色预测模型。
这些统计模型计算简捷,已被广泛应用到大坝安全监控的各个领域,但针对自变量因子与效应量之间非线性和小样本问题都存在一定的不足,特别是模型的泛化能力更严重影响到模型的预警。
相关向量机(RVM)是由 Tipping[9]在稀疏贝叶斯理论的基础上,将极大似然估计、先验概率和后验分布估计等理论结合形成的一种监督型机器学习算法。与神经网络和支持向量机相比,RVM 算法的相关向量数目较少,模型的复杂度较低,且其选取的核函数无需满足 Mercer 条件的限制,另外该算法的模型可调节参数不多,在一定程度上减少了因参数设置不当而影响模型泛化性能的风险[10]。
杜传阳等[11]建立了以 RVM 为理论基础的时间序列模型并应用于大坝安全监控。唐琪等[12]在大坝变形预测时利用马尔科夫链模型,对 RVM 模型得到的残差数据进行修正。张海龙等[13]在某重力的位移监测中使用了模糊均值聚类算法,对聚类后的样本运用 RVM 算法进行了训练。王娟等[14]将核独立分量分析与 RVM 相结合,对某拱坝的缺失监测数据进行了插值处理。相关研究结果均表明,相较传统的统计模型,RVM 整体上在大坝安全监测方面表现更为出色,但 RVM 模型研究对模型参数的选取仍严重依赖人为经验,为此利用粒子群算法(PSO)针对 RVM 模型参数优化问题,对 PSO-RVM 模型进行改进,并在此基础上进行相关监控研究。
1 PSO-RVM 模型
从相关向量机的基本原理可以看出,相关向量机的性能与选取的径向基核函数参数γ有很大关系,因此,研究寻找最佳核函数参数γ具有重要的实际意义。为解决该问题,结合 PSO 算法和 RVM模型的特点,采用 PSO 算法对 RVM 模型的关键参数γ进行寻优,建立起 PSO-RVM 模型,借助 PSO算法优秀的全局搜索能力实现模型的优化,旨在提高监控模型的学习和泛化能力。
1.1 PSO-RVM 模型参数选择
PSO 算法本身参数众多,选择合适的参数有利于提高算法的性能和效率。在实际应用中,需要调节的参数主要有以下几种:
1)适应度函数F(·)。适应度函数是用来对种群中各粒子的适应性进行度量的函数[15],适应度函数越小,则对应的粒子个体被选中作为最优解的机会越大。结合模型评估需求,选择常用的模型评价指标均方根误差作为适应度函数,公式如下:
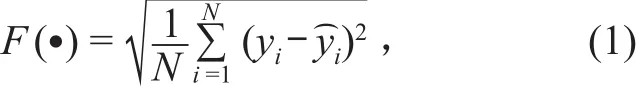
式中:N表示种群规模;yi和分别表示模型因变量的实测值和预测值。
2)种群规模N。研究发现,在 PSO 算法中,当待优化参数维数不大时,种群规模即粒子个数一般取 10~30 个就能得到比较好的结果,种群规模越大,模型收敛速度越慢[16]85。本研究中,PSO 算法优化 RVM 模型时维数是 1,考虑到大坝安全监控模型在实际应用中的及时预报需求,选择种群规模N= 10 个。
3)惯性权重ω。惯性权重ω代表以前速度对当前速度的影响。根据文献 [16] 的建议,将最大和最小惯性权重设置为ωmax= 0.9,ωmin= 0.4。
4)加速因子S1和S2。S1和S2分别用来调整粒子在飞行过程中自身学习和群体协作的能力比重,其取值大小直接影响粒子的运动轨迹。在类似的大坝安全监控模型研究中发现,S1=S2= 1.5 时,模型具有较好的收敛效果[16]88。
5)最大迭代次数Niter,max。迭代次数越多,获得参数最优解的可能性越大,但同时模型整体的训练时间越长,且容易产生过拟合现象[17]。因此,本研究设置最大迭代次数Niter,max= 100 次,兼顾模型的预报精度和计算复杂度。
6)速度变化区间 [vmin,vmax]。为防止搜索发散,PSO 算法中通过设置区间对粒子的飞行速度进行限制,将粒子超出边界值的速度设定为边界值,本研究设置vmin= -1,vmax= 1[16]89。
7)位置变化区间 [Xmin,Xmax]。为保证粒子在搜索空间内的飞行位置可解释,还需使用位置变化区间对粒子的位置进行限制,将粒子在运行中超出边界值的位置设定为边界值。理论上,RVM 核参数γ的取值范围为(0,+ ∞),但缺乏最大位置Xmax的限制,同样会产生搜索发散问题,导致模型拟合时间过长[18],参考大量研究发现,合适的核参数γ一般不超过 20,因此本研究设置Xmin= 1,Xmax= 30。
1.2 PSO-RVM 模型流程
本研究选择径向基函数作为 RVM 模型的核函数,利用 PSO 算法对核函数参数γ进行优化,构建起智能相关向量机模型——PSO-RVM 模型,用于大坝安全监控。在 PSO 优化 RVM 参数之前,需先将预处理后的数据按一定比例划分为训练集和测试集两部分,其中训练集用于模型构建及参数寻优,测试集用于模型评价。训练集与测试集的划分比例并没有严格的要求和标准,本研究取 90% 的数据作为训练集,余下 10% 的数据作为测试集。
PSO-RVM 模型结合了 PSO 算法,弥补了RVM 模型的不足,使得大坝安全监控模型的学习和泛化性能得以提高,PSO-RVM 模型整体的算法步骤是 PSO 和 RVM 2 种模型算法步骤的结合, PSORVM 模型流程图如图 1 所示。
2 工程实例
2.1 工程概况
某工程混凝土面板堆石坝最大坝高为 111 m,坝顶长度为 348.2 m,坝顶宽度为 10.0 m,上游综合坡比为 1∶1.40,下游综合坡比为 1∶1.55,坝顶高程为 805 m,同时坝顶设有高度为 5.2 m 的 L 型防浪墙与面板相接。混凝土面板为不等厚,厚度t= 0.3 +0.003H(H为水深)。
为保证大坝的安全运行,该工程配设了较为全面的安全监测系统,既包括上、下游水位,气温和降水量等常规监测项目,也涵盖大坝坝体的变形、沉降等监测项目。本研究选用工程主坝 TB5 视准线的监测数据,该视准线于 2012-05-17 开始监测,每隔 7 d 完成 1 次观测记录。将 2015-03-10 作为监测基准日,选取该测点自 2015-03-17 至 2017-11-29共 90 个位移监测数据作为训练集,选取该测点自2016-12-06 至 2017-02-07 共 10 个位移监测数据作为预测集,通过建立 PSO-RVM 模型预测后 10 个监测日,也就是预测集的位移数据。
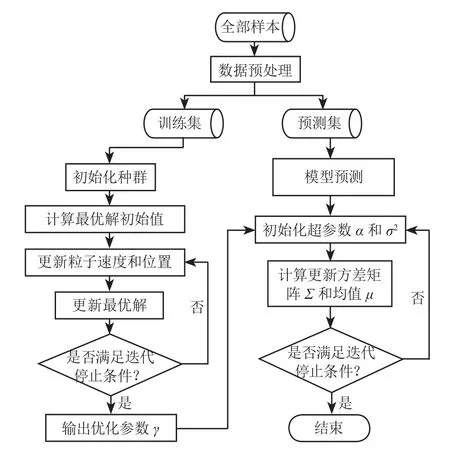
图1 PSO-RVM 模型流程图
2.2 大坝安全监控模型
2.2.1 模型选择
混凝土面板坝位移的统计模型如下:
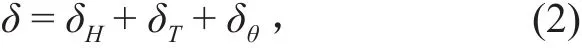
式中:δ代表位移总量;δH,δT,δθ分别表示水压、温度和时效等分量。
1)水压分量δH。库水压力作用在坝体上产生的内力会使坝体变形而产生位移。混凝土坝上任一观测点的水压分量δH与水深H,H2,H3呈线性关系,即
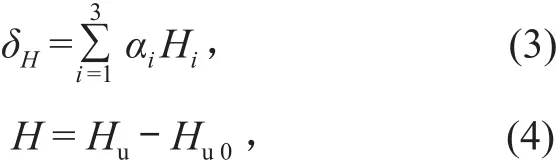
式中:Hu,Hu0分别为坝体位移监测日和监测基准日的上游水头;αi为水压因子回归系数。
2)温度分量δT。温度分量δT是由坝体混凝土和基岩温度变化而引起的大坝位移,从力学观点看,δT应选择坝体混凝土和基岩的温度计测值作为因子,但由于坝体内部实测的和基岩的温度监测数据的缺失,故采用多周期的谐波作为因子,即
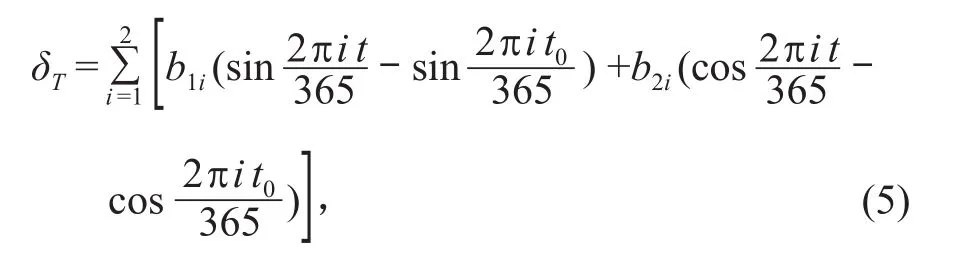
式中:t为坝体位移监测日到监测基准日的累计天数;t0为建模数据对应的监测日到监测基准日的累计天数;b1i,b2i为温度因子回归系数。
3)时效分量δθ。时效分量与大坝位移之间的关系复杂,它综合反映了混凝土坝体和基岩的徐变,同时还包括坝体裂缝引起的不可逆位移。混凝土坝的时效分量δθ包含时间Tθ的线性和对数函数,即

式中:Tθ为坝体位移监测日到监测基准日的累计天数除以 100,即Tθ=t/100;Tθ0为建模数据对应的监测日到监测基准日的累计天数除以 100,即Tθ0=t0/100;c1,c2为时效因子回归系数[19]。
根据分析,本研究选择的模型因子分别如下:水压分量,Hu-Hu0,(Hu-Hu0)2,(Hu-Hu0)3;温度分量,时效分量lnTθ- lnTθ0。为简化起见,将这 9 个分量分别命名为X1~X9。
2.2.2 模型评价指标
选取标准均方误差和平均绝对百分比误差 2 种统计指标作为 PSO-RVM 模型的评价指标,以此检验模型的泛化性能。
2.2.3 数据预处理
为消除数据量纲的影响,需要对原始数据进行标准化预处理,本研究采用零均值标准化。
对缺失值进行插补处理,本研究采用线性插值方法,利用缺失值前后监测日的监测数据进行计算插补。
2.3 结果分析
2.3.1 模型参数的寻优结果分析
本研究 RVM 模型核函数参数γ的取值为 3,而通过粒子群算法寻优得到的核函数参数γ为 6.9137。
粒子群算法在寻优过程中适应度函数值的变化曲线如图 2 所示,可以看出,当优化代数达到 20 代时,适应度函数值趋于稳定,当优化代数达到 30 代时,适应度函数值恒定不变。此时粒子的个体最优解Pbest和种群的全局最优解Gbest已经产生且不再更新,这也意味着粒子的速度和位置不再发生大的变化,种群逐渐收敛至一点。
2.3.2 模型的稀疏性能分析
RVM 和 PSO-RVM 模型训练样本和相关向量关系展示如图 3 和 4 所示,拟合时段相关向量个数与运行时间如表 1 所示。
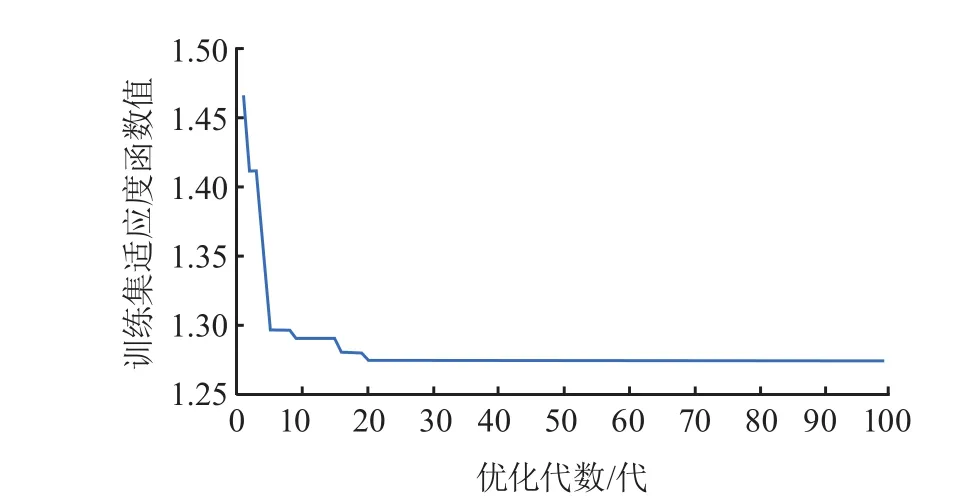
图2 训练集适应度函数值变化曲线

图3 RVM 模型的相关向量个数
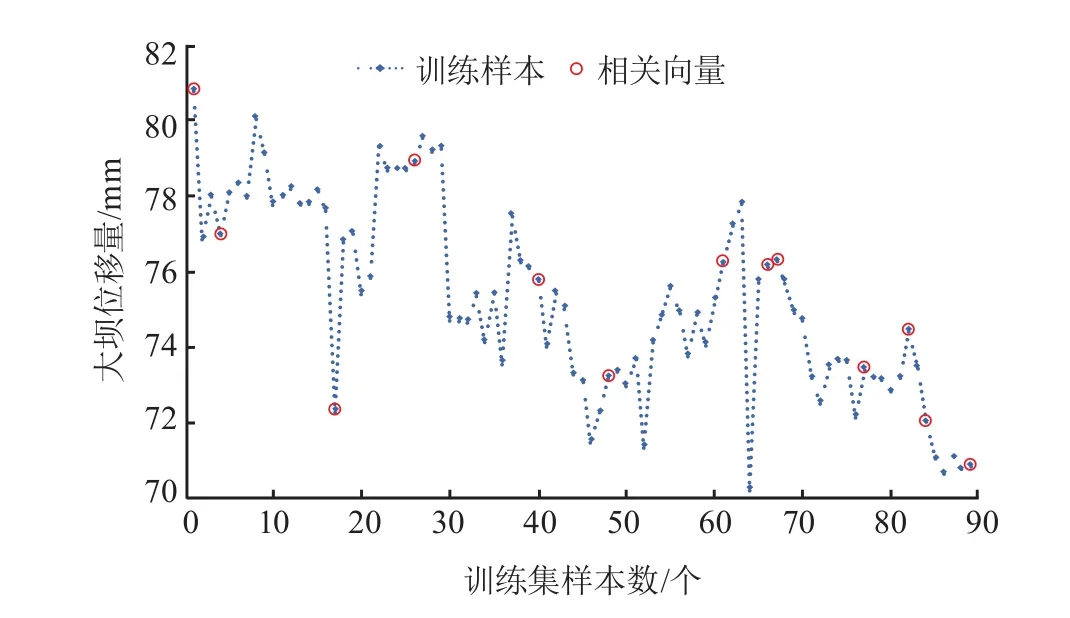
图4 PSO-RVM 模型的相关向量个数
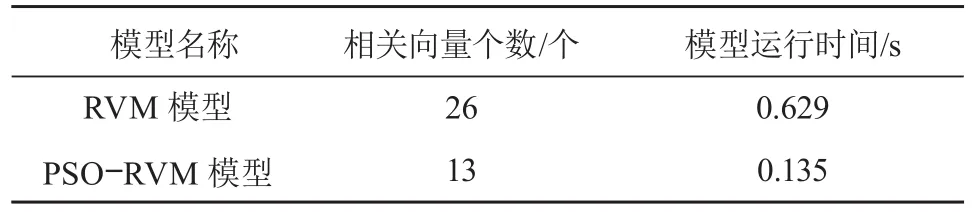
表1 RVM 和 PSO-RVM 模型拟合时段相关向量个数与运行时间
其中,PSO-RVM 模型的相关向量数为 13 个,即模型训练完成后仅保留 13 个样本量,少于 RVM模型,同时,由表 1 可以看出 PSO-RVM 模型的运行时间要少于 RVM 模型,说明 PSO-RVM 模型的稀疏性能更好。考虑到大坝安全监控中实时预测的需要,监控模型对于预测的及时性有着更高的要求,因此,PSO-RVM 模型更适用于大坝位移量的在线预测,更能满足大坝安全监控模型实时预测的要求。
2.3.3 模型的学习性能分析
模型的学习性能主要通过模型在训练集上的预测均方根误差体现,RVM 和 PSO-RVM 2 种模型拟合时段的均方根误差分别为 1.249,1.274,PSORVM 的均方根误差稍大于 RVM,但两者十分接近且数值理想。
RVM 和 PSO-RVM 模型在训练集上的拟合曲线如图 5 所示。
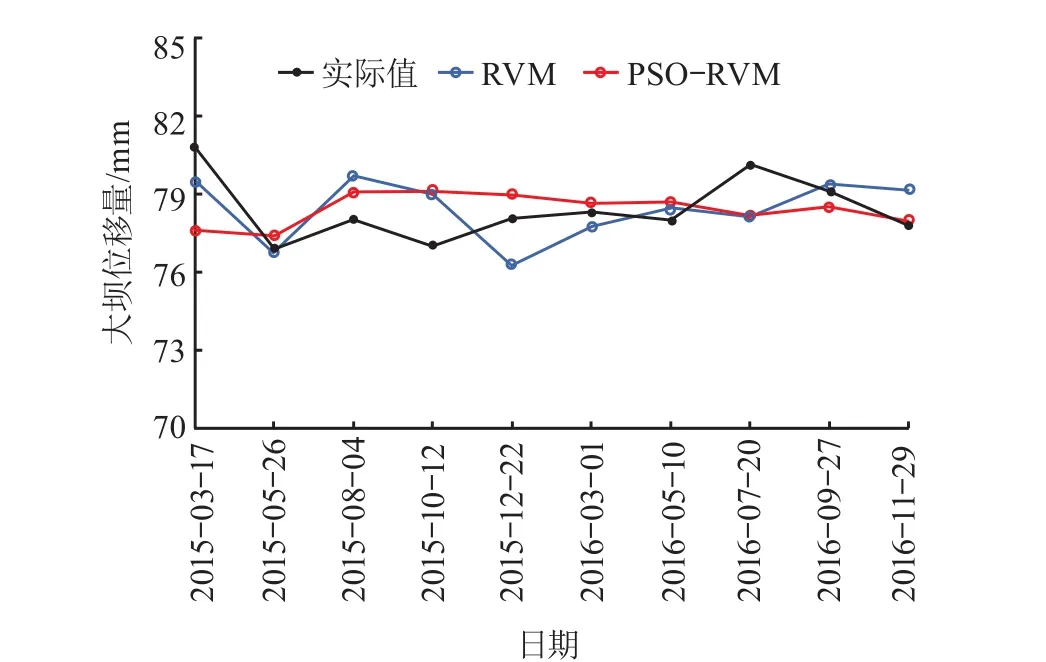
图5 RVM 和 PSO-RVM 模型的拟合曲线
从图 5 可以看出,不管是 RVM 模型还是PSO-RVM 模型,其拟合曲线都紧密围绕理论值上下波动,说明两者拟合效果良好,都具有不错的学习性能。
2.3.4 模型的泛化性能分析
与学习性能相比,大坝安全监控模型更加看重其泛化性能即预测未知数据量的能力,从而发挥风险预报的作用。RVM 和 PSO-RVM 模型的预测结果分析如表 2 所示。
从表 2 可以看出,PSO-RVM 模型的预测值比RVM 模型的预测值更加接近实际值,且 PSO-RVM模型预测的相对误差显著小于 RVM 模型,说明优化后的 PSO-RVM 模型比未优化的 RVM 模型预报精度更高。
RVM 和 PSO-RVM 模型的预测曲线如图 6 所示。从图中可以直观看出,PSO-RVM 模型预测曲线比 RVM 模型的预测曲线更加接近理论值,同样体现了优化后的 PSO-RVM 模型具有更好的泛化性能。2 个模型评价指标如表 3 所示。
由表 3 可以看出,PSO-RVM 模型在 2 种评价指标上的表现均显著优于 RVM 模型,可知经过粒子群算法优化后的相关向量机模型预测精度更高,泛化性能更强。

表2 RVM 和 PSO-RVM 模型的预测值和相对误差
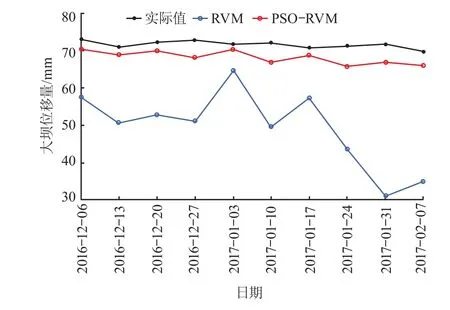
图6 RVM 和 PSO-RVM 模型的预测曲线

表3 RVM 和 PSO-RVM 模型的评价指标对比表
3 结语
通过对相关向量机模型的粒子群优化和工程实践检验,可得出如下结论:1)与常规 RVM 模型相比,PSO-RVM 模型能显著提高 RVM 模型的稀疏性和泛化性能;2)PSO-RVM 模型可以应用于大坝安全实测数据的建模和分析。与现有的研究成果相比,本研究方法编程简单,原理清晰,但如何提高模型的通用性,从而针对不同核函数或多核函数提出优化改进是下一步研究重点。

