基于文化-禁忌搜索算法的巡飞弹航迹规划*

黄雨杨,郝 峰

(西安现代控制技术研究所, 西安 710065)

0 引言

随着技术的发展,以巡飞弹、无人机等为主的无人飞行器的集群作战,成为了现代战争的一种重要形式,而巡飞弹的航迹规划则是其集群作战任务规划的一个重点。航迹规划是一个NP-hard问题,需要良好的算法保证规划的完备性和高效性。近年来,国内外的研究以航迹规划为目标设计了多种算法,例如,步长可变的稀疏A*算法[1],自适应学习粒子群算法[2],遗传算法与蚁群算法的组合算法[3],结合Voronoi图的遗传算法[4],基于文化算法的改进算法[5-6],以及新出现的以灰狼算法[7]、蝗虫算法[8]为例的仿生算法等。

文中设计了基于文化算法与禁忌搜索算法的组合算法,并加入变异机制和Boids模型分离机制。同时,通过作战环境和任务的建模,对算法进行航迹规划仿真,并与其它算法相比较,验证了本算法全局搜索速度和局部搜索能力的改善。

1 算法简述

1.1 文化算法

文化算法(culture algorithm,CA)的概念由Reynolds于1994年引入[9],算法模拟对象为以人类为例的高等动物种群进化过程。搜索空间由信仰空间和种群本身组成,种群的进化受到信仰空间的指导,而种群的进化结果也会影响信仰空间,帮助信仰空间完成更新。两个空间互相影响进化,从而可以得到先进的个体。算法两层空间分别以不同的速度进行更新,且相互影响,对于解决复杂的优化问题具有明显的优势。通过改变文化知识的更新方式、种群受知识的影响速度、两层空间之间信息的传播方式等途径,可以对文化算法进行优化[10-11]。

1.2 禁忌搜索算法

禁忌搜索算法(tabu search,TS)是一种现代启发式算法[12],是对人类智能记忆机制的模拟,通过禁忌表和特赦准则控制搜索空间。该算法全局搜索能力强,能有效防止陷入局部最优的问题,但其本身依赖初始解的选取,不良的初始解会大幅增加搜索时间。近年来的算法研究设计中,通常将禁忌搜索算法与其余仿生算法结合成组合算法,提高算法的搜索效率[13]。

2 航迹规划问题建模

2.1 环境模型及代价函数

巡飞弹执行任务时受到的环境威胁,主要分为地形威胁和敌方防备威胁。构造多个二元指数函数,可以分别建立山峰、坡地、谷地模型,求和后即为整体地图模型。考虑到实际地形的起伏性,在地形上添加小幅白噪声函数,使之更接近真实情况。

敌方防备威胁主要有雷达威胁与防空导弹威胁。分别记两种威胁概率为Pradar和Pmissile,记雷达在半径R1内探测概率固定,且最大探测半径为R2;记导弹杀伤概率为Rkill,最大探测半径为Rmax,则有相应模型为:

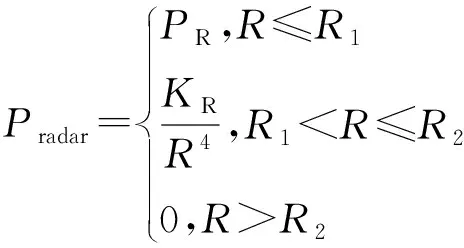
得到各威胁概率后,即可得到全地图威胁模型,建立代价函数。本模型构建的航迹代价受航迹长度、威胁概率以及爬升高度影响,具体为C=∑[w1f1(li)+w2f2(pi)+w3f3(hi)]。式中f1(li)、f2(pi)、f3(hi)分别为基于航迹长度、威胁概率、爬升高度计算得到的代价函数,分别乘以权重后得到总航迹代价。

2.2 巡飞弹约束条件

巡飞弹的航迹需要满足如下约束条件:

1)最大转弯角:巡飞弹转弯时,转弯角不能超过规定值；

2)最大爬升/俯冲角:巡飞弹在上升和下降时爬升/俯冲角不能超过规定值；

3)最小直飞距离:巡飞弹在任意航迹段中保持直线飞行状态,到端点附近开始转弯，而巡飞弹不能一直保持转弯状态,需在转弯后直线飞行一定距离；

4)最大航迹距离:由于燃料有限,巡飞弹的航迹总长有最大距离限制；

5)最小飞行高度:巡飞弹飞行过程中,需要保持距离地面一定的高度；

6)到达目标方向角:巡飞弹到达目标时存在方向角约束,即末端航迹的方向角需在一定范围内。

2.3 搜索空间建模

根据地图和威胁模型,可对搜索空间进行建模。设定一个威胁概率上限p,高于这一概率的区域视为禁飞区。确定禁飞区后,在地图中将其对应高度修改,使高度明显大于其余区域。根据代价函数和威胁模型,不难得出,在同一水平位置,当巡飞弹保持较低高度飞行时,无论是防空导弹威胁概率还是爬升高度代价都相对较低,所以,为了简化搜索空间,降低搜索耗时,可以将三维空间转化为二维的最小威胁曲面[14],在曲面上进行搜索规划,提高搜索效率的同时,保证尽可能低的路径代价。曲面建立规则如下:

1)根据最小飞行高度及地图各点海拔,确定各点的最低高度。

2)剔除禁飞区,设置禁飞区内点的曲面高度为-5 000 m，并记录,以便区分。

3)针对山峰模型,考虑到峰顶高度较高,在爬升角受限的情况下会拔高整个地图,从而导致代价和威胁概率明显提高。因此,将山峰处坡度较大点所包围的山峰部分设置为禁飞区,进行剔除并记录。

4)从所有可飞点中选取最高点,根据最大爬升/俯冲角约束提升其周围所有可飞点对应曲面高度,然后再以这些扩展点为中心,进一步提升外侧可飞点对应曲面高度,直至更新所有点高度,以保证各点之间的路径可飞,从而完成最小威胁曲面的构建。

3 算法设计与实现

3.1 航迹编码及迭代方法

本次规划设定起始点坐标为(50 m,50 m),目标点坐标为(10 000 m,10 000 m),最小直飞距离为200 m。考虑到只在最小威胁曲面上搜索,故每条航迹的编码均为行数为2的矩阵,每一列代表对应航迹点的坐标。定义基础航迹为:

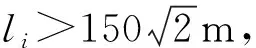
生成新航迹的操作为将两条可飞航迹的水平面坐标按随机比例组合,所得结果为水平坐标编码,可保证航迹同样位于最小威胁曲面上。因此,只需要检测新航迹是否满足转弯角约束和禁飞区限制,即可判断其可飞性。

3.2 Boids模型分离机制

使用文化算法需要防止子代过于接近,因此,采用Boids鸟群模型中的分离机制,即鸟群个体间距离过近时,会选择分离,防止碰撞[15]。分离机制具体表现为,若子代集中为一个解或全部存在于禁忌表中,则对种群进行分离操作,将规范知识恢复为初态,保留种群1/10的染色体,随机生成剩余染色体,得到新的种群;同时,在单次迭代中提高变异概率,以加强全局搜索。这一方法能有效防止解过于集中导致后续搜索失去意义,同时分离机制也能提高“爬山”能力,跳出局部最优解。

3.3 算法步骤设计

为了提高后期的局部搜索能力,引入变异机制,具体为采用生成初始航迹种群的规则,在最小威胁曲面上,按照3.1的规则随机改变一部分的航迹点。

采用禁忌表对形势知识的更新进行限制,优先将不属于禁忌表的较优航迹选作形势知识,利用形势知识的改变来更改种群的进化方向。同时,按照3.2中的分离机制,建立知识的重置规则,加强算法跳出局部最优解的能力。

算法具体步骤如下:

1)设置各项参数,按3.1的规则生成初始种群。分离标志初态为0。

2)沿两侧边界得到两条航迹,作为规范知识。对初始种群按可飞性分类,分别选取最优航迹。若最优可飞航迹代价更小,则作为形势知识;反之,则按两航迹代价占比,从两者中随机选择一条航迹作为形势知识;若不存在可飞航迹,则选择最优不可飞航迹作为形势知识。若存在可飞航迹,选取最优可飞航迹为初始最优解。

3)若分离标志为1,则按3.2所述分离机制进行分离操作。重置规范知识,保留当前种群最优的1/10,其余染色体按照3.1的初始航迹种群生成规则重置。

4)根据信仰空间及变异机制产生子代,并计算其代价及可飞性。

5)按代价对两代航迹进行排序,随后确定新种群。优先选取可飞且代价较小的航迹,其余航迹以可飞性划分,按比例分别选取相对较优的航迹。

6)按接受概率及新的种群更新信仰空间,利用禁忌表限制形势知识的选取。若种群中所有航迹均处于禁忌表中,则取代价最小的航迹作为形势知识,同时将分离标志置为1;否则,按2)的规则选取航迹作为形势知识,同时将分离标志置为0。

7)根据航迹代价选取最优可飞航迹,与当前最优解比较,更新最优解。

8)若迭代满足终止条件,则输出最优解为最终规划航迹;否则,返回步骤3)。

4 算法仿真

4.1 离线航迹规划

仿真使用PC机处理器为Intel® Xeon® CPU E3-1230 v6 @ 3.50 GHz,在Matlab 2016a上进行。在2.3中建立的搜索空间模型中进行航迹规划。设计仿真种群个体数为40,迭代次数为80,进行仿真,得到航迹如图1所示,搜索时间为15.61 s,航迹代价为15 946.21,长度为15 577.39 m,平均高度为254.22 m。实际上,在本模型中,从不同侧绕过威胁区域,可得到若干个局部最优解,而仿真可得其余所有局部最优解的最小代价在16 400附近。故而本次规划航迹与最优解相近,并未陷入局部最优解中。最优解航迹代价与迭代次数关系如图2所示。

图1 规划所得航迹

图2 最优航迹代价-迭代次数折线图

可以看出,10次迭代内,搜索已迅速找到全局最优解所在区域,此时搜索耗时在3 s以内,而在之后的搜索中,利用变异机制和分离机制能不断得到代价更小的航迹。由此可见,改进的文化-禁忌搜索算法在全局搜索和局部寻优上效果良好。下文分别采用文化算法,带变异的文化算法(culture algorithm with mutation,CAM),以及粒子群算法(particle swam optimization,PSO)在本模型上进行航迹规划。调整迭代次数,使各算法消耗时间相近,各运行100次,结果如表1所示。此外,使用步长固定的稀疏A*算法进行规划并比较。

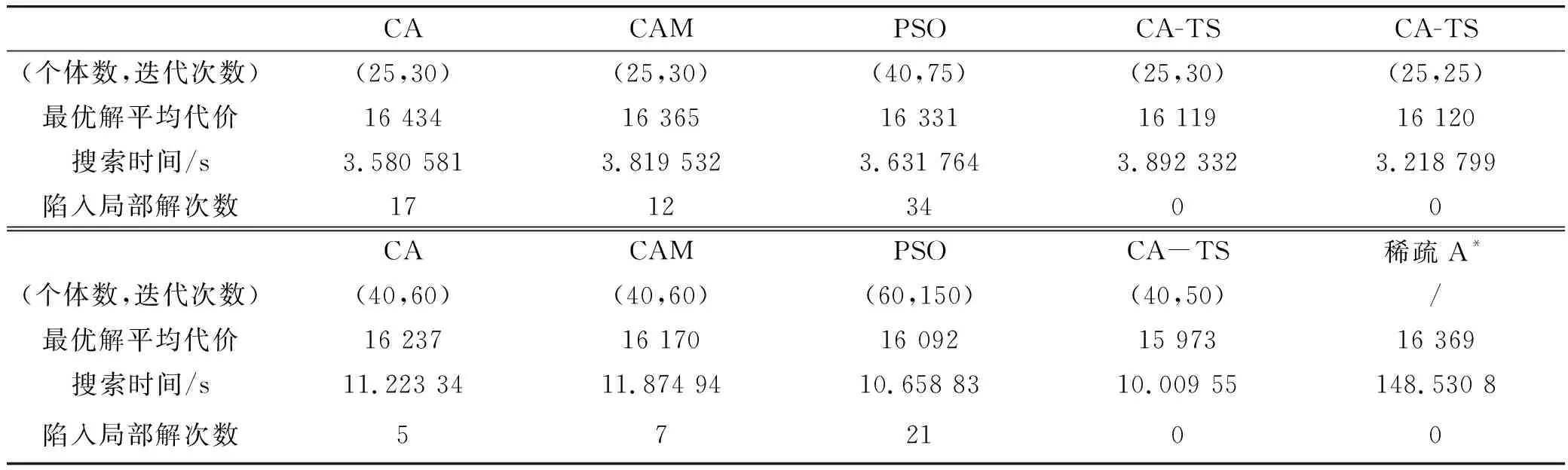
表1 不同算法的航迹规划结果

比较数据可看出,改进的文化-禁忌搜索算法虽然每次迭代耗时略高,但由于全局搜索和局部搜索能力的明显优势,能在更小种群、更少迭代次数下,得到代价更小的航迹,同时还改善了其余算法可能陷入局部最优解的缺点。此外,与步长固定的A*算法相比,本算法受网格化约束程度小。由此可见,本算法无论在航迹规划,还是在其他复杂优化问题中,都具有良好的性能。

4.2 实时航迹规划

在先前的仿真中,采用改进的文化-禁忌搜索算法可以在较短时间内得到较理想的航迹,故可利用这一性能,减少迭代次数,进行实时航迹规划。巡飞弹按离线规划的航迹飞行,途中检测到威胁区域变化,随后预留一定的飞行时间(本次仿真设为5 s),以该时间后的下一个航迹点作为起点,进行航迹规划,规避新的威胁。在不同的飞行时间将其中一个雷达威胁的中心由(7 500 m,5 000 m)移动至(8 500 m,5 000 m),分别进行实时航迹规划,结果如图3所示。两次规划分别耗时3.45 s、3.47 s,航迹可飞且代价较小,满足要求。

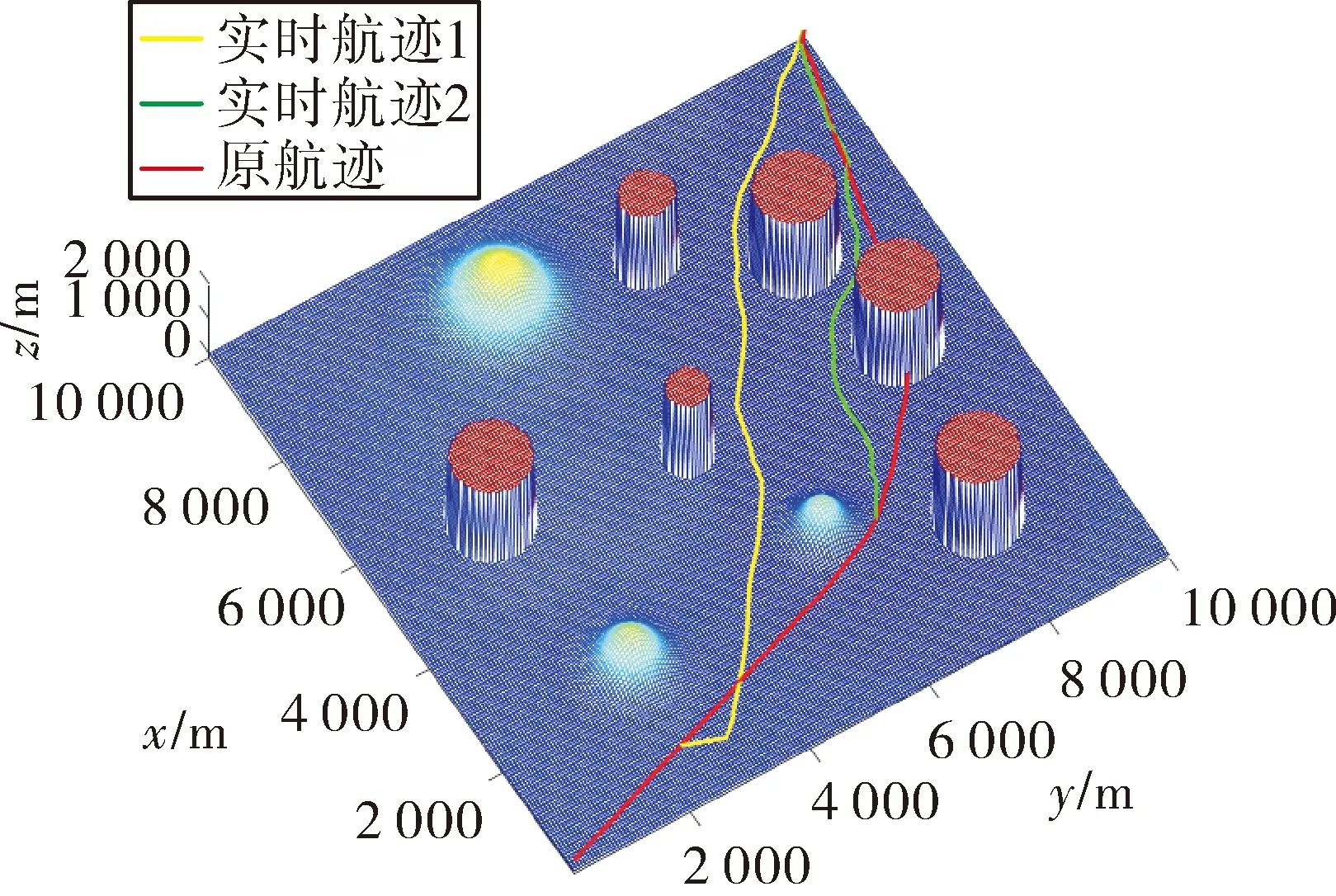
图3 实时规划航迹

5 总结

文中将文化算法与禁忌搜索算法相结合,并加入变异机制,以及Boids鸟群模型的分离机制,对算法性能进行了优化,得到了改进的文化-禁忌搜索算法。相比于其他各类算法,本算法能在短时间内跳出局部最优,有助于快速规划航迹;而当规划时间充足时,迭代后期算法的局部寻优能力良好。因此,本算法性能优势明显,对于理论上和工程上的航迹规划均有很大作用。