基于S型曲线加减速的机器人圆弧轨迹规划与仿真

丁猛 张中辉 刘蔚钊

摘要：轨迹规划算法在机器人控制中的地位十分重要，其优劣会直接影响机器人的运动速度、精度以及平稳性。结合康尼公司设计的KNT-ESR6B机器人，针对传统加减速算法的运动加速度突变所造成的机器人运动抖动问题，提出了基于S型曲线加减速的空间圆弧轨迹规划算法，并在Matlab平台进行了仿真实验。

关键词：机器人;轨迹规划;S型曲线;圆弧插补

0    引言

从规划空间上可将机器人轨迹规划分为两种，即关节空间轨迹规划和笛卡尔空间轨迹规划。在工业生产中，机器人运动轨迹几乎都是直线和圆弧轨迹的组合[1]，特别是在一些对机器人运动轨迹有着严格要求的工业现场，如喷涂、焊接、打磨等，其圆弧轨迹规划的平滑度直接决定了机器人的运动性能，所以轨迹规划算法在机器人控制中的地位十分重要。

本文以南京康尼公司自主研发的KNT-ESR6B型六自由度机器人为研究对象，基于S型曲线加减速对其空间圆弧插补轨迹规划进行了研究，并在Matlab平台对其进行了仿真验证，结果表明，机器人的圆弧运动轨迹平滑，各关节加速度平缓，满足应用要求。

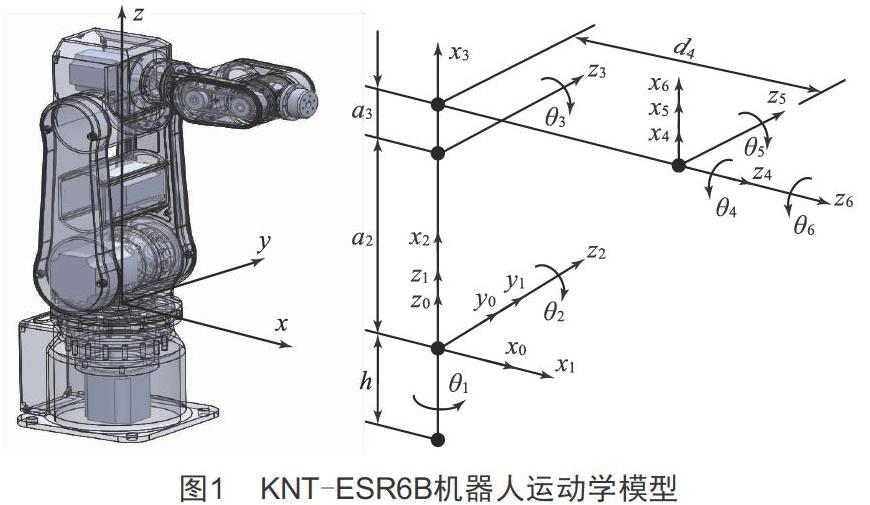
1    KNT-ESR6B机器人

KNT-ESR6B机器人由机械本体和控制系统两部分组成，机器人本体的6个关节由交流伺服电机驱动，从而实现机器人的运动;其控制系统则采用了“PC机+DSP运动控制卡”的开放式控制模式来设计。根据连杆坐标系的规则建立了KNT-ESR6B机器人运动学模型，如图1所示。

通过相邻连杆坐标系之间的关系变换矩阵，即公式（1），可得KNT-ESR6B机器人各相邻连杆之间的变换矩阵，由此可以推导出机器人正向运动学和逆向运动学公式。

2    基于S型加减速曲线的空间圆弧插补算法

2.1    机器人空间圆弧插补

机器人空间圆弧插补算法比较复杂，其解决思路是将空间圆弧转化到平面中进行处理[2]，如图2所示，已知机器人工作空间中圆弧的起点P1（x1，y1，z1）、中间点P2（x2，y2，z2）和终点P3（x3，y3，z3），具体插补步骤如下：

（2）求坐标变换矩阵。以O1（p0）为原点，圆弧所在平面M的法向量a为O1Z1轴，向量■为O1X1轴，根据右手定则建立新坐标系O1-X1Y1Z1，其中O1Z1轴在基础坐标系O-X0Y0Z0中的方向余弦即为法向量a，由公式（3）平面M的方程可求得法向量a：

最后由右手定则可知，O1Y1轴的法向量o=a×n，所以利用新坐标系O1-X1Y1Z1的各轴在基础坐标系O-X0Y0Z0中的方向余弦向量，就可建立变换矩阵：

所以对于基础坐标系中的任意一点0p=（0px，0py，0pz）都与新坐标系中与之唯一对应的点1p=（1px，1py，1pz）来表示，两者之间的转换过程如式（10）所示：

（3）在新坐标系中计算各插补点的坐标值，然后将空间圆弧轨迹上各插补点坐标值从新坐标系O1-X1Y1Z1转换到基础坐标系O-X0Y0Z0中。如圖3所示，在新坐标系O1-X1Y1Z1的X1Y1平面中确定插补角大小，即：

在公式（11）中，由于用到了atan2（x，y）函数，该函数本身具有预先判断目标点所在象限的功能，会对角度θ进行处理，所以不再需要对插补的方向和过象限进行判断。

设在机器人插补周期T内，每次插补角度增量为Δθ，则插补的次数N=θ/Δθ+1（N四舍五入取整数），根据公式（12）可求出轨迹中每个插补点1pi=（1pix，1piy，1piz）所对应的坐标值，即：

最后根据公式（12）将平面圆弧的每个插补点坐标通过转换矩阵映射到基座标系中，再由逆向运动学公式求出轨迹上插补点所对应的关节角度[3]，驱动机器人运动到相应的角度位置，就可以完成空间圆弧的轨迹规划。

2.2    S型加减速曲线

S型加减速将T型加减速的3段过程拓展为7段，如图4所示，即由加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段、减减速段组成，可使速度曲线更加趋于平滑，减小电机突然启动时的冲击和机器人关节机构机械振动，保证机器人运动的平稳。

在图4中，t为时间坐标，ti为各阶段的过渡点时刻，Ti为各阶段的持续运行时间，为了简化计算公式的复杂程度，用τi=t-ti-1（i=1，2，…，7）表示各阶段的起始点作为时间零点的时间，即局部时间坐标。同时假设加加速度和减减速度都为J，且最大加速度为Am，即T1=T3=T5=T7=T，初始速度为Vs，最大速度为Vm，则通过对每段过程的分析，可得对应轨迹段的加速度函数，分别为：

通过对每个阶段加速度函数进行积分运算，即可得出速度函数，为：

对公式（14）中各阶段的速度以公式（15）进行积分，即可得到运动的位移函数：

2.3    基于S型加减速曲线的圆弧插补

通过上述对圆弧和S型曲线的分析，给定机器人圆弧轨迹的初始位置P1、中间点P2、终点P3，由公式（6）（11）可得出机器人在新坐标系下的圆弧半径r和圆心角θ2，则机器人运动的圆弧轨迹位移L=rθ2[4]。

设S曲线的初始速度和终止速度为Vs，最大速度为Vm，最大加速度为Am，加加速度和减减速度为J，可得各阶段的运行时间：

根据机器人空间圆弧插补的原理，设计其插补控制程序，流程图如图5所示。

3    圆弧轨迹规划仿真实验

以KNT-ESR6B教学机器人为实验平台，在其工作空间中选定不共线的三点，即起始点P1、中间点P2、终点P3，其位姿数据如公式（17）所示（假设运动过程中姿态保持不变）：

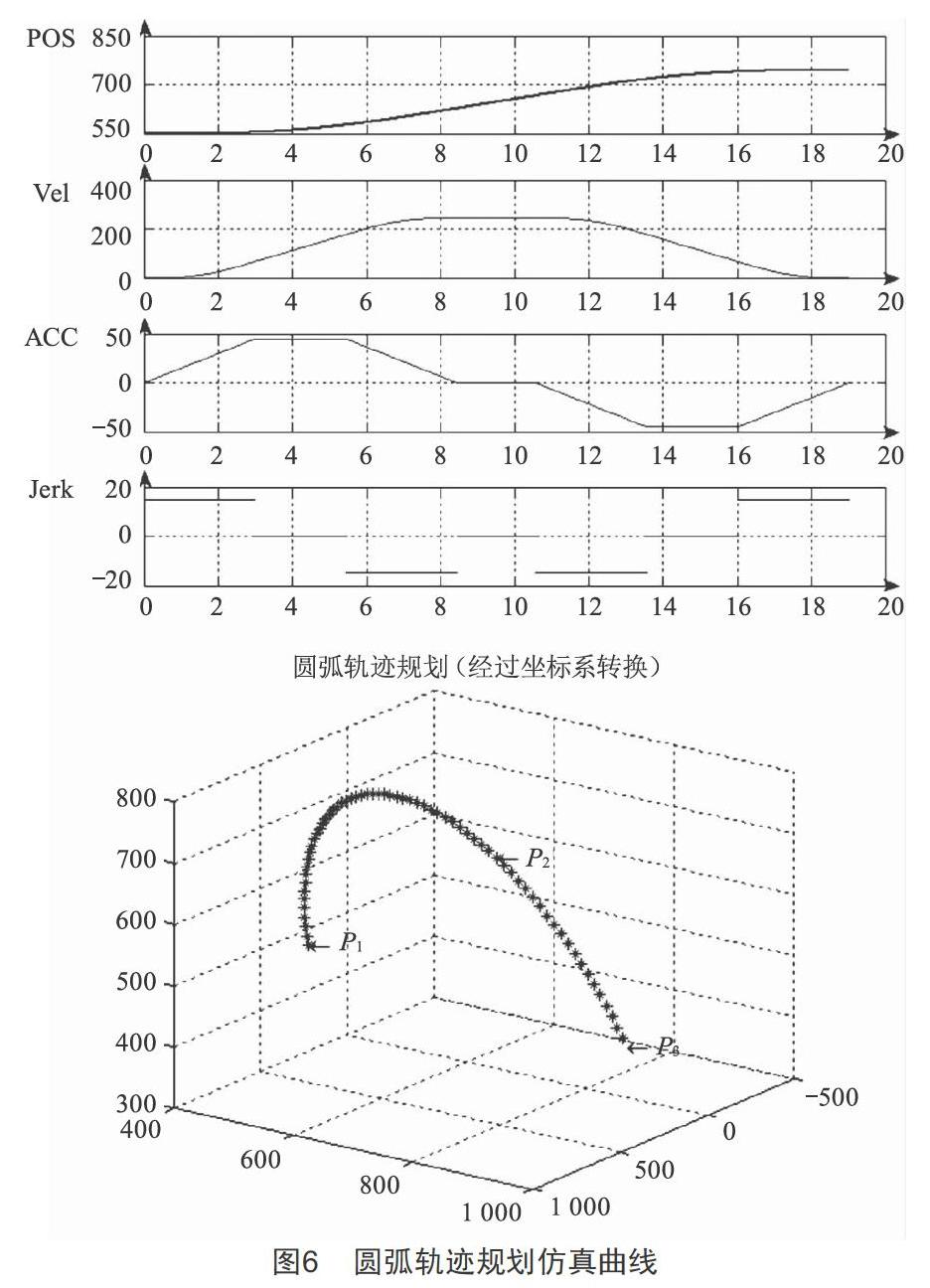
在Matlab平台基于S型加减速曲线对空间圆弧插补算法进行仿真，其圆弧插补过程中各轴坐标变化曲线以及圆弧插补的运动轨迹如图6所示。

通过以上仿真图形数据可以看出该机器人进行插补时的运行轨迹，验证了基于S型曲线加减速的机器人空间圆弧插补算法的可靠性。

4    结语

本文基于S型加减速曲线对机器人空间圆弧轨迹规划进行了研究，通过坐标系转换矩阵，将基坐标系下的圆弧轨迹转换至圆弧所在平面的新坐标系下，完成了插补过程;同时针对轨迹规划曲线的平滑性要求，运用S型加减速曲线进行升降速控制，通过仿真结果看出运用S型加减速控制使得轨迹规划曲线趋于平滑，可以减小电机加减速时所造成的机器人运动抖动。仿真的结果验证了所提算法的可靠性，为KNT-ESR6B机器人的控制实现提供了理论依据，具有一定的实用价值。

[参考文献]

[1] 蔡自兴.机器人学基础[M].北京：机械工业出版社，2015.

[2] 孙瑛，程文韬，李公法，等.关节型机器人轨迹规划算法及轨迹规划研究现状[J].长江大学学报（自科版），2016（28）：32-38.

[3] 张霞，孙强，蔡顺燕，等.机器人轨迹规划控制策略研究[J].微电机，2019（11）：76-81.

[4] 刘蕾，柳贺，曾辉.六自由度机器人圆弧平滑运动轨迹规划[J].机械制造，2014（10）：4-5.

收稿日期：2020-04-09

作者简介：丁猛（1981—），男，江苏南京人，工程师，研究方向：自动控制。