基于量子神经网络的地层对比研究①

王伟，赵娅，李盼池

(1.广东石油化工学院 石油工程学院，广东 茂名 525000；2.东北石油大学 计算机与信息技术学院，黑龙江 大庆 163318)

地层对比是油气田勘探与开发工作中进行油藏描述及多井评价的重要组成部分[1,2]。地层对比最常用的方法是根据单井测井曲线特征在某一层段上的最大相似性原则来完成的。但该方法在油田开发后期，对比工作量大，并且陆相三角洲沉积横向砂体不稳定、相变快，过度依赖专家经验，限制了对比结果的正确性。近年来，基于测井曲线的人工智能自动地层对比方法逐渐成为领域研究热点，其中较流行的方法有：人工智能方法[3-5]、字符串动态匹配算法[6-8]、BP神经网络方法[9-13]、智能算法[14-18]等。这些方法有一定的成效，甚至已经应用到商业化软件上，但其效果依然难以让人满意。如目前应用效果最好的BP神经网络方法识别准确度高，但是在网络模型训练时需要大数据样本，这对于数据样本少的情况不适用。

针对这些存在的问题，本文提出一种基于量子神经网络(Quantum Neural Networks，QNN)的多井井间小层自动对比方法。利用测井曲线及其统计特征数据构造网络模型，实现基于QNN的小层自动对比。旨在构建具有收敛速度快、逼近精度高、泛化能力强等优点的网络模型，在兼顾准确性的前提下，提高地层对比工作的效率。

1 量子神经网络模型及算法

研究表明，人脑信息处理的过程可能与量子现象有关，大脑中可能存在量子力学效应，量子系统具有与生物神经网络相似的动力学特征[19]。量子神经网络是量子计算和神经计算相融合的结果，将神经网络和量子计算理论相结合能更好地模拟人脑的信息处理过程。量子神经网络中的“量子”，是指量子计算的某些原理和方法。在传统神经网络中引入“量子”的目的，是借助量子计算的某些机制(如量子比特的旋转)来提升网络的逼近及泛化能力。

1.1 量子神经元模型

图1 量子神经元模型 图2 量子神经网络模型

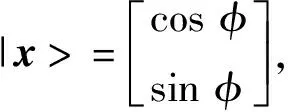
此时，量子神经元的输出为

(1)

1.2 量子神经网络模型

本文采用的三层量子神经网络(见图2)，其中输入层、隐层和输出层分别有n、p、m个量子神经元，网络输出为量子神经元处于状态|1>的概率幅。

|hj>=[cosαj，sinaj]T

(2)

yk=sinβk

(3)

量子神经网络需要训练的参数包括：γk，ξk，ϑjk，λj，φj，θij，这些参数可以通过梯度下降法训练。参数调整规则可统一描述为β(t+1)=β(t)+ηΔβ(t+1)，其中β分别为θij、ϑjk、φj、ξk、λj和γk，而η为学习速率。

2 基于QNN的地层对比

本文采用Matlab语言进行QNN网络模型的编程，对朝阳沟油田6口已经人工分层的标准井共计126个小层进行了地层对比仿真实验，其中5口井(105个小层)用于训练，1口井(21个小层)用于测试。再利用构造的模型对全区366口井进行地层对比。将地层对比分为二级地层对比和三级地层对比。二级地层对比，小层类别包括10类：F11(包括F111～F115)、F12(包括F121～F122)、F13(包括F131～F132)、F14、F15(包括F151～F152)、F16(包括F161～F162)、F17(包括F171～F172)、F21(包括F211～F212)、F22(包括F221～F222)、F23；三级地层对比包括21个小层类别。

2.1 特征参数选择

选择对岩性敏感的测井曲线作为进行地层对比的主要依据，此外反应各井单砂层测井曲线形态的一些特征向量值，也是优秀的地层对比指标[20]。本文选定地层对比的特征参数有：小层厚度，自然伽马(GR)、自然电位(SP)、声波时差(AC)、深侧向电阻率(LLD)4条测井曲线的均值，中位数、相对重心X、相对重心Y、锯齿数、方差变差等5种统计特征，组成特征向量，构造井间小层对比的输入样本。所选的特征参数有助于网络模型构造高质量的训练样本，极大地提高了网络模型的训练能力及泛化能力。

2.2 测井曲线滤波去噪和归一化

原始测井曲线数据存在的噪声，会影响QNN的识别效果，因此需要进行滤波处理。本文采用经典的沃尔什滤波方法。该方法先对测井曲线实施离散沃尔什变换[21，22]，忽略某些高频分量之后，再进行反变换重构原曲线。为消除不同量级数据之间的相互影响，对所选4条曲线数据进行归一化处理。

2.3 构造样本数据

参与对比的10个特征参数中，小层厚度可根据测井解释结果获得；自然伽马、自然电位、声波时差、深侧向电阻率从测井曲线上获取；中位数、相对重心X、相对重心Y、锯齿数、方差变差为单个数值，它们均来自于自然伽马曲线的离散数据[23]。

2.4 样本数据量子态描述

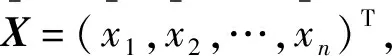
|X>=[|x1>，|x2>，…，|xn>]T

(4)

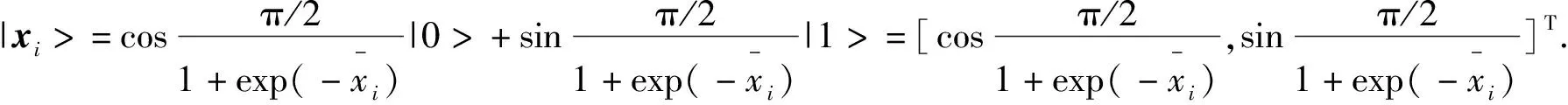
对于所有实值样本，应用式(4)即可转换为可以提交QNN训练的量子样本。

2.5 构造QNN模型

将样本数据分为训练集和测试集两部分，训练集用于QNN的网络训练，使网络模型逼近样本特征和小层类别之间隐含的复杂非线性映射关系；测试集用于检验QNN的泛化能力。关于QNN模型参数设置，输入节点个数等于小层特征参数个数(10个)；网络的输出为小层类别，只用1个输出节点即可；隐层节点一般没有确定规律可循，通过多次实验来获取。训练后的网络模型即可用于目标小层类别的对比。

本文方法是以整口井为单位进行小层识别的，对于处理好的单口测试井数据，若该井没有断层，则输出小层类别应满足固定层序；若某层违反了层序，则该层可认为是断层。

2.6 与BP神经网络模型应用对比

为验证QNN在地层对比方面的性能，本文采用QNN与BP神经网络对比。为了使对比更加充分，本文使QNN和BP分别在不同隐层节点和迭代次数下独立运行100次，然后取平均识别率作为对比指标，隐层节点具体取1，2，…，10，迭代次数分别为50，60，80，100，120，140，160，180，200。三级地层对比QNN和BP网络模型对测试集的识别实验结果见表1。

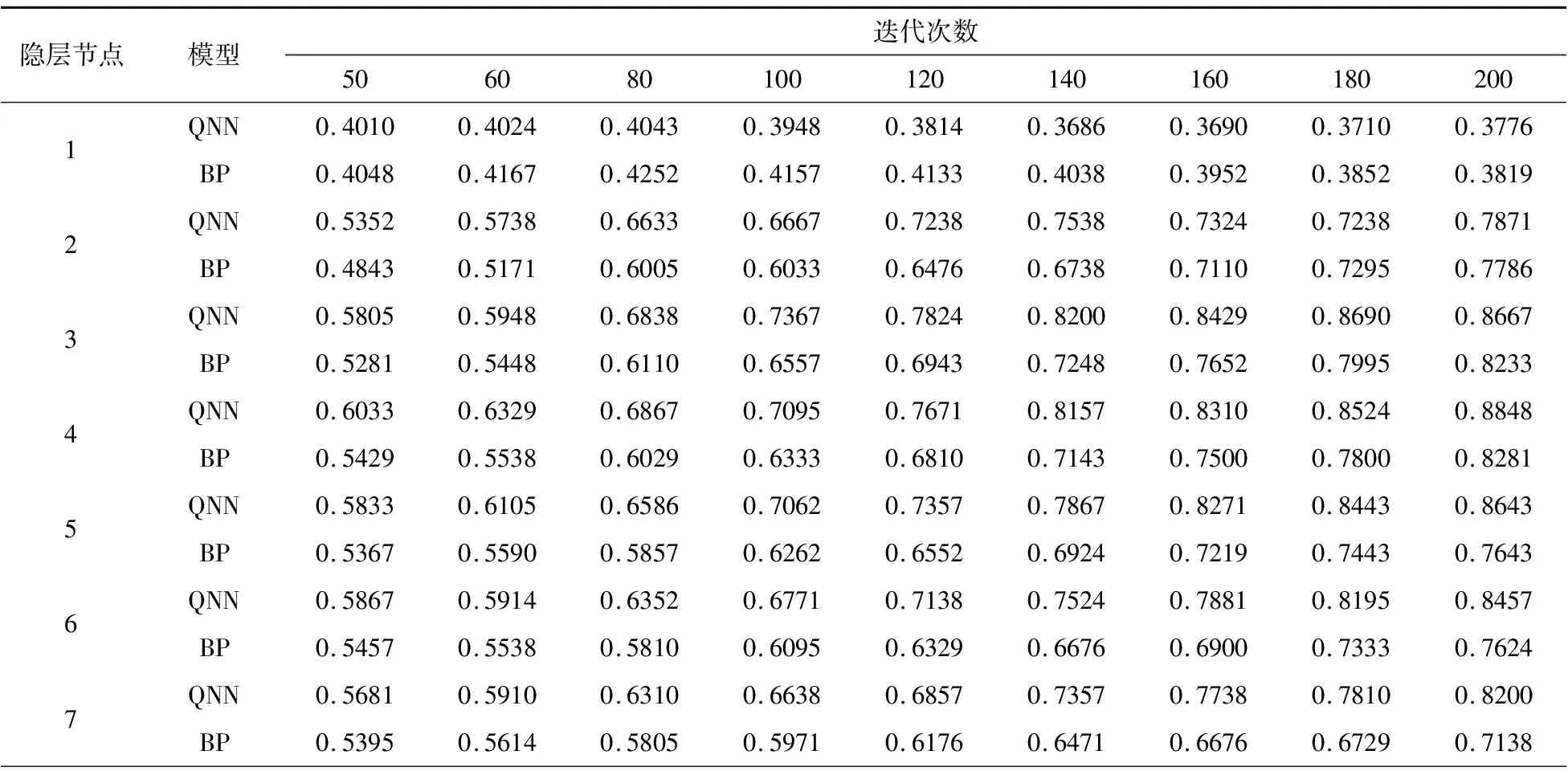
表1 三级地层对比QNN和BP网络模型对测试集的识别结果

由表1可知，对于三级地层对比，当隐藏节点为4，迭代次数大于140时，QNN识别率均在80%以上，最高值为88.48%，而BP网络识别率最大值仅为82.81%。QNN优于BP神经网络，这主要是在QNN中引入了量子机制。在QNN中，通过量子旋转门和受控量子旋转门的协同作用，增强了网络的学习能力、模式信息概括能力、函数逼近能力以及泛化推广能力，从而使QNN在少量数据样本的情况下依然表现出良好的适应性。

3 基于QNN的地层对比结果

利用该模型对全区366口开发井进行地层对比工作，三级小层对比的正确率最高可达88.48%。以F142-X井为例，对该井的10个二级分层和21个三级分层进行识别，结果见图3。

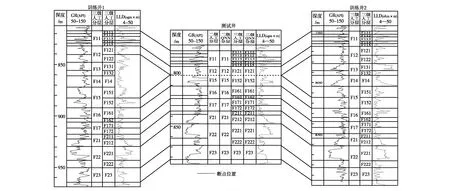
图3 测试井人工分层与QNN分层结果对比

由图3可知，该井的二级分层识别均正确，仅三级分层F111小层被识别成F112。造成原因是F111的地层厚度小，导致所含的特征测井曲线数据量不足，这说明要达到较高的识别率，地层需要一定的厚度，以增加测井曲线数据量。根据识别的结果与正常的层序，可以有效地确定该井的断点位于F12与F15之间(F122～F151断失)。

4 结论

(1)量子神经网络算法通过量子旋转门和受控量子旋转门的协同作用，增强了网络的学习能力、模式信息概括能力、函数逼近能力以及泛化推广能力，从而使QNN较其它智能算法，在少量数据样本的情况下依然表现出更好的适应性。

(2)根据QNN识别后所输出小层层序是否间断，能够判断该井是否存在地层断失情况及断点位置。

(3)利用构建的QNN网络模型，对长46地区366口井进行地层对比，三级小层对比的正确率可达88.48%，证明采用量子神经网络解决地层对比中工作量大、砂体相变快、地层断失等问题是可行、有效的。