中国地方政府债务持续期的空间生存分析
李方方,王周伟,赵海鹏
(上海师范大学 商学院,上海 200234)
一、引 言
近十多年来,中国地方政府债务规模连续快速增长。截至2019年底,中国地方政府债务总余额为21.3万亿元,平均地方政府债务率(债务余额/综合财力)高达82.9%。虽然总体上可控,但个别地方政府的债务风险已经远超出警戒线,如青海的负债率(地方政府债务余额/GDP)已达70.88%,贵州、宁夏、内蒙古和海南也均超过40%。另一方面,地方政府的可偿债收入增幅锐减,融资能力受限。随着经济结构性调整不断深化,中国经济与区域经济步入中低速增长的新常态,中国地方政府的财政税收收入增长幅度收窄,使得土地财政依赖度很高。然而,“房住不炒”定位下的严格调控,致使土地拍卖收入持续减少,不稳定性剧增,地方政府的融资能力也因此受挫,“借新还旧”还债策略难以为继。在此背景下,亟需从可持续性视角对地方政府债务规模与风险进行分析,掌握地方政府债务持续期的影响因素,利用地方政府债务持续期分布及其组合优化,做好逆周期审慎监管和跨期管理。
现有文献对中国地方政府债务风险测度做了一些有益的探讨。如利用综合评价法评估地方政府债务风险压力程度[1],利用结构化建模法测度地方政府债务的预期违约风险[2],或是利用logit模型等统计计量建模法估算地方政府债务违约率与限额[3];利用BP神经网络、贝叶斯网络或支持向量机等机器学习方法,分类预警地方政府债务风险[4-6],或从可持续性视角分析地方政府债务流动性风险[7]。以上文献从不同视角评估了地方政府债务违约风险,但局限于静态视角,没有考虑未来经济行为的变化。从建模方法适用性来看,以上文献有两个局限性:一个是地方政府信用度较高,融资能力较强,违约样本占比很少,信贷记录数据长度短而且不完整;二是地方政府债务期限都很长,很难获得具体债务违约时间数据,通常包含删失数据,因此很难用单一分布描述预测地方政府债务风险损失。另外,区域经济之间是相互关联的,这些关联促成了区域经济关联网络,使得地方政府债务风险具有传染性[8]。而现有文献多是在封闭经济中测度单一省市政府的债务风险,没有考虑地方政府债务风险之间的空间溢出关联作用。
为弥补上述研究的局限性,本文尝试在区域经济异质关联网络中从时间维度估算地方政府债务可持续性风险。首先以修正的KMV模型为框架,推导出区域经济关联背景下地方政府债务持续期的理论分析方程,分析其影响因子;其次,考虑到地方政府债务风险数据删失特性,使用带有异质项的空间生存分析模型估算债务持续期,测度地方政府债务风险。
二、理论分析
(一)地方政府债务可持续期估算分析
假设某经济体由区域1和区域2两个地区(地方)组成,不妨以区域1为研究对象,对于区域2,同理可得类似结论。各区域的要素禀赋不变,要素在两个区域之间可以自由流动。区域经济关联主要是通过要素流动与商品贸易及共同联动而相互关联,其中商品贸易通过市场潜能反映。设在t时刻区域1的市场潜能为:
(1)
其中,Mt1为t时刻区域1的市场潜能;yt1和yt2分别为时刻区域1和区域2的经济体系实际产出;d11为区域1的内部直径距离;d12为区域1中心和区域2中心之间的最短距离。
要素自由流动,则在t时刻区域1的修正C-D生产函数为:
yt1=(a1At1)(b1Kt1)α1(c1Lt1)β1Mt1
(2)
其中,yt1是在t时刻区域1的总产出;At1、Lt1、Kt1分别是在t时刻区域1的技术水平、劳动力和资本禀赋;a1、b1、c1分别是在t时刻区域1的技术水平、劳动力和资本禀赋等生产要素的利用系数,如果大于1,说明有从区域2流入区域1的生产要素;α1、β1分别为资本与劳动力要素投入产出弹性。
定义本期的可偿债收入小于本期的债务还本付息额为地方政府违约事件[2]。利用修正KMV模型,可知在t时刻区域1地方政府发生债务违约风险事件的理论预期违约率pt,1取决于违约距离DDt1,而违约距离又决定于地方政府的可偿债收入、本期债务还本付息额、财政收入增长率及其标准差与持续期。即有:
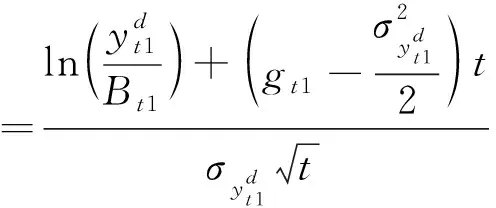
(3)
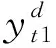
观察期内地方政府的生存时间为T,定义为首次违约时间,即从期初t=0时刻至t=T-1时刻违约距离大于0,而在t=T时刻违约距离小于0。可用数学公式表示为:
T=inf{tDDt≤0,且,DDt-1≥0},
t=0,1,2,…,T
(4)
由此可知,生存时间主要决定于生存时间期末时刻T的违约距离。由于T期之前的违约距离为先定变量,生存时间T与违约距离DD之间的因果关系可以简约地设定为:
T=aa0+aa1DDT
(5)
式(5)说明,地方政府债务生存时间长短决定生存时间期末时刻T的违约距离。
(二)地方政府债务可持续期的影响因素分析
由式(5)可知,地方政府债务持续期由式(3)中的各项因素决定,其中地方政府收入主要来自税收收入与土地拍卖收入,t时刻区域1地方政府能够用于偿还债务的可偿债收入(即可支配财政收入)为:
(6)
其中,τ1是在t时刻区域1的平均税率;P是在t时刻该经济体的名义价格水平;wt1为取决于财政分权制度的在t时刻区域1的可偿债收入占比;wt l为在t时刻区域1的土地拍卖收入占比。
式(3)中,Bt1等于未到期债务余额的利息与到期债务余额的本利和,则有:
Bt1=rt∑MV+(1+rt)MVt
(7)
其中,∑MV是未到期债务的总金额;MVt是到期债务金额;rt是地方政府债务的融资成本,即借款利率;地方政府债务风险主要是信用风险,借债利率主要取决于信用风险溢价,不妨假设,它决定于无风险利率与负债率,即:
(8)
财政收入增长率gt1。地方政府债务具有经济增长效应。地方政府举借(清偿)债务,会增加(减少)本区域经济中的流动性,再通过事权、基础设施投资与官员绩效竞赛等渠道,提高(降低)投资机会与投资规模,推动(拉低)区域经济增长[9]。以人均方式表示的地方政府债务的经济增长效应等式为:
gti=α1gt-1,i+α2dbt,i+α3kt,i+α4liqt,i
(9)
其中,gti表示区域经济增长率;dbt,i表示地方政府债务负担率;kt,i是存量资本;liqt,i是区域流动性;αi,i=1,2,3,4,大于0。
综合依据上述生存时间分析模型,可以总结出图1所示的地方政府债务可持续时间及其影响因素作用路径的理论分析框架。进一步本文提出如下命题:中国地方政府债务持续期主要受11个影响因素的影响,其作用路径和预期作用效果汇总如表1所示。

表1 地方政府债务风险变量选择与说明
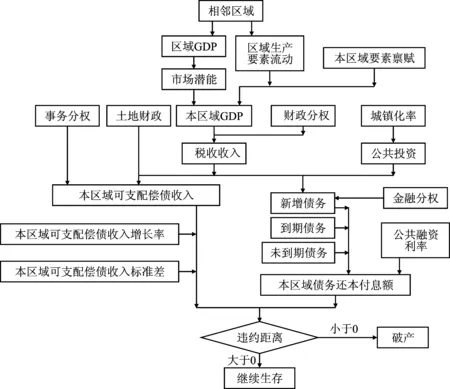
图1 理论分析框架
三、变量指标选择与样本数据
(一)变量指标选择
本文设定地方政府违约为兴趣事件,构建生存分析模型研究地方政府从样本初期至违约事件发生的动态过程。按前文的定义,违约事件定义为可偿债收入小于当期偿债规模。本文选取40%作为偿还比例[2];偿债规模为各地方政府本期期末债务余额的利息支付额加上本期到期债务的本利和;地方政府债务的平均期限取各期限债务的加权平均年限;根据当年地方政府债务自发自还债券情况,债务利率选用对应平均期限的地方政府债券实际票面利率的上限。
为了得到回归结果的无偏估计,本文选取全国31个省市为研究对象来解决左删失数据问题,即保留在观测样本开始前(1998年)没有违约的省份。值得注意的是,对于地方政府而言,即使发生违约,由于它们具有较强的资源支配与融资能力,以及财务预算的软约束,地方政府债务很难会破产,实际观测中它们会继续生存下去。反之,如果在样本期间,该样本区域的地方政府债务没有发生违约事件,则该样本数据为右删失数据,在整个分析期中就需要保留这些样本区域,由此得到地方政府最长的持续时间为18年。本文主要解释变量的定义及符号如表2所示。
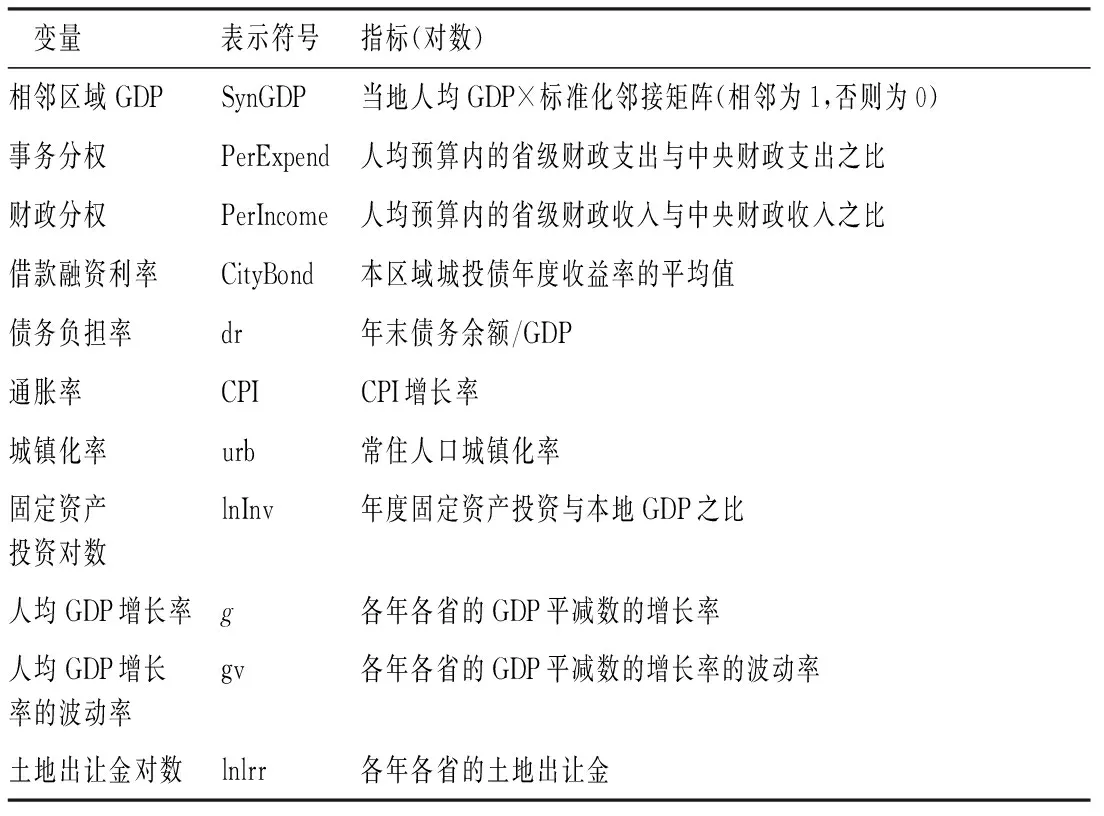
表2 地方政府债务风险变量选择与说明
(二)样本与数据
2015年之后中央政府对地方政府债务采取以预算和限额管理为主的防控体制。为控制经济环境变量,本文选取中国省级地方政府为样本,收集1998—2015年的相关变量原始数据,来源为《中国统计年鉴》《中国国土资源统计年鉴》《中国财政统计年鉴》《中国金融年鉴》和Wind数据库,缺失数据部分,根据相关公式和变化规律利用插值法推算补齐。为了消除异方差和量纲上的差异,本文在实证研究中对相关变量数据做了自然对数处理。
四、实证结果与分析
为进一步证实前文提出的命题假设,综合区域经济异质关联和数据左删失问题,本文使用空间生存分析模型进行实证检验。先给出地方政府生存时间的Kaplan-Meier非参数估计,使用PH生存分析模型进行基本验证;为避免遗漏变量对模型估计的影响,再进一步使用带有异质项的空间生存分析模型进行验证;最后对该实证结果做稳健性检验。
(一)生存函数的Kaplan-Meier非参数估计
记地方政府连续存活时间T超过某一生存时间长度t的概率为生存函数S(t):S(t)=P(T>t)=1-F(t),生存函数的非参数估计可由Kaplan-Meier估计量得到,表达式为:
(10)

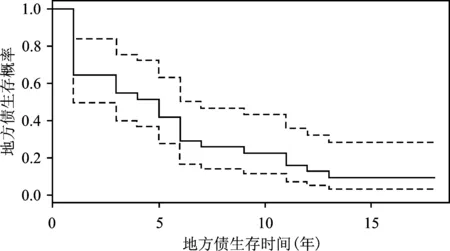
图2 地方政府债务的生存曲线
从表3的KM估计量结果可知,地方政府在第1年的生存概率只有0.607 1,即在本文违约条件的设定下,第1年年末只有约60%的地方政府能够生存下来,另外40%的地方政府因可偿债收入少于债务还本付息额导致违约;仅约35%的地方政府生存至第5年。观察期第12年末,地方政府债务不违约的概率仅为0.035 7。
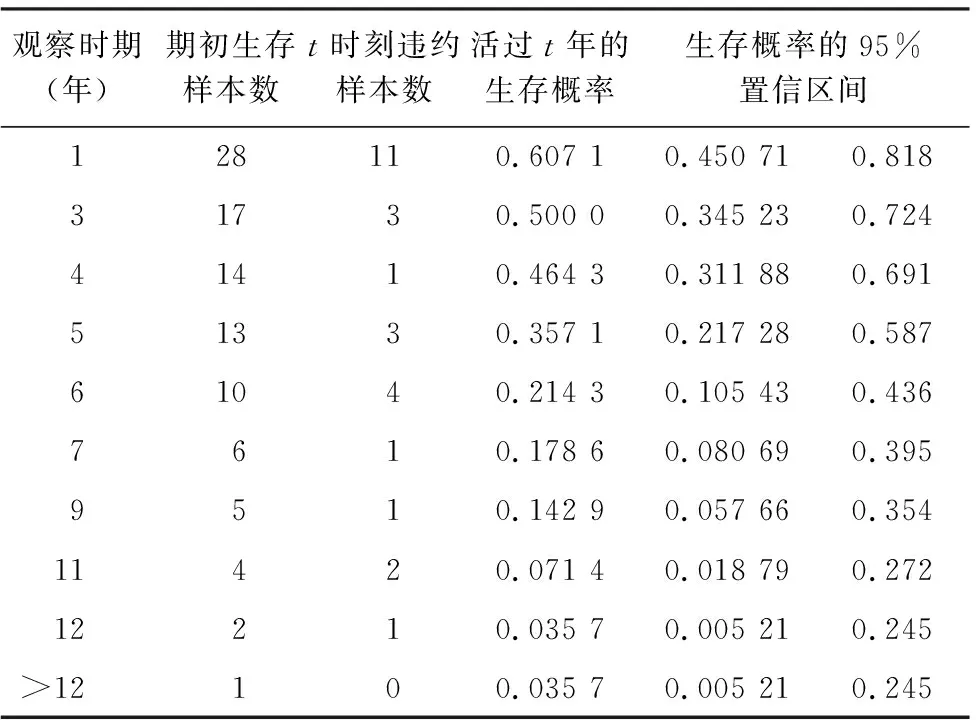
表3 Kaplan-Meier估计结果及生存曲线
图2给出了更为直观的KM生存曲线。容易看出,随着时间的推移,地方政府债务不违约事件的概率(即生存概率)逐渐降低。此外,随着持续期的增加,地方政府的生存概率趋于稳定;KM曲线先陡峭后平稳,前期违约的个体较多,风险较大,后期违约概率较小,风险较低。
(二)模型形式的有效性识别
设地方政府的风险函数为λ(t),表示地方政府在t时刻之前未发生债务违约而在t时刻发生债务违约的概率:
(11)
其中,f(t)为生存时间T的概率密度函数。由于真实的持续时间还依赖于某些解释变量,此时风险函数可表示为λ(t,xi,β)。其中,xi为个体i的解释变量向量;β为待估参数。根据风险函数的设定不同,可将常见的生存模型分为三类:比例风险模型(Proportional Hazard,PH),比例优势模型(Proportional Odds,PO)和加速失效时间模型(Accelerated Failure Time,AFT)。以上三种模型均属于半参数模型,参数估计时需要先给出xi=0时的S0(·)的参数分布或者非参数先验分布。本文中对每个模型选择非参数函数TBP(Transformed Bernstein Polynomial)来近似S0(·)的不同先验参数分布:log-logistic分布、Weibull分布和log-normal分布。为了比较不同参数分布的不同模型的有效性,本文使用DIC、LPML和WAIC三个信息准则指标评估模型选择的适当性。DIC综合测量模型的拟合优度和有效参数数目,越小越好;LPML和WAIC专注于评价模型的预测性能,LPML越大越好,而WAIC越小越好。评价结果如表4所示。
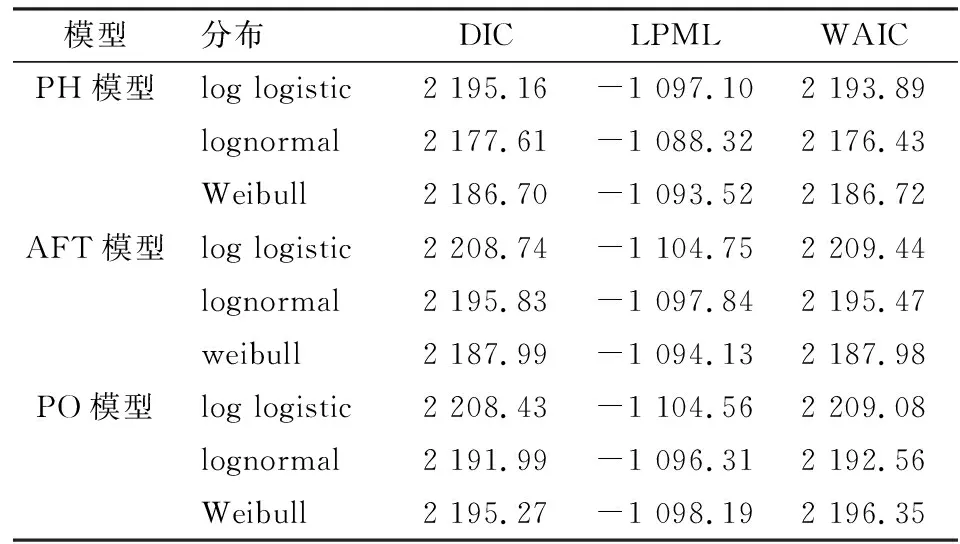
表4 普通半参数生存模型的评价结果
根据三个信息准则筛选标准,三个模型的回归结果高度一致,三种评价方法均显示PH模型优于AFT模型和PO模型。PH模型应选择lognormal分布,AFT模型选择Weibull分布,PO模型选择lognormal分布。因此,空间生存分析模型的基本形式应当选用lognormal分布的PH模型,运用空间比例风险分析模型(SPH)验证估算区域异质关联框架中的地方政府债务的可持续期。
(三)实证结果与分析
空间比例风险分析模型是在PH模型中引入空间异质性关联作用因素。
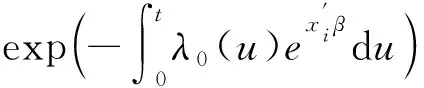
(12)
对风险函数两边取对数可得:
(13)
其中,系数β可解释为解释变量对风险函数的半弹性,eβ为对应的“风险比率”;S0(t)为解释变量为0时对应的基准生存函数。
2.独立个体异质的空间比例风险分析模型。上述非空间的PH模型假设影响地方政府生存时间的所有风险因素都包含在解释变量xij内,但实际上样本个体在空间上可能存在“不可观测的异质性”(Unobserved Heterogeneity,又称为脆弱性,Frailty)。空间生存分析中“不可观测的异质性”可划分为共享异质性(Shared Frailty)和个体异质性(Individual Frailty)两种,前者将个体分组,假设组内的个体具有同质性,不同组的个体之间具有相互独立的异质性;后者不对个体分组,假设个体之间存在不相关联的异质性。由于地方政府之间不存在天然分组,故本文只考虑第二种个体异质性。加入个体异质性得到个体异质的空间比例风险分析模型,其个体风险函数为:
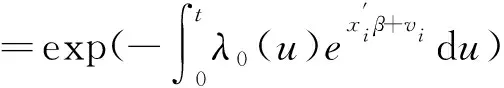
(14)
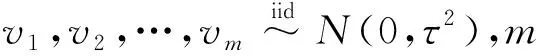
3.异质相关的空间比例风险分析模型。前文的理论分析已经证明,地方政府的债务风险之间具有空间关联性,则个体脆弱项vi不再相互独立而是表现出空间自相关性。考虑地方政府数据的“格栅数据”特征,本文使用区域方法来研究地方政府债务风险的空间关联性。区域方法需要明确空间“邻接”的具体含义,“邻接”可以是字面意义上基于地理相邻关系的邻接,也可以是经济意义上的邻接。地理相邻可用简单的m×m空间邻接矩阵表示相邻关系,此时相邻矩阵E中的元素eij以是否在地理上一阶相邻为判断标准来进行赋值,如果区域i与区域j相邻则为1,否则为0,同时设定eii=0。在研究经济问题时,常用的空间权重矩阵为考虑到“逆经济距离”指标后的空间经济权重矩阵A*,定义为:
A*=AE
(15)
(16)
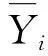
确定空间相邻关系后,个体脆弱项vi具有了空间相关性,确定n维随机变量v的联合密度函数成为研究的关键点。从贝叶斯估计的视角,通常的做法是在vi的先验分布中加入空间相关性,给定包含邻接信息的条件自回归(CAR)先验分布[10],则脆弱项的条件分布为:
i,j=1,2,…,m
(17)
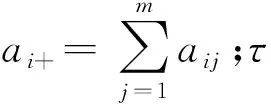
(四)空间比例风险分析模型的实证结果与分析
表5列出了非空间PH模型、独立同分布异质的空间PH模型(IID-SPH)和网络关联个体异质的空间PH模型(CAR-SPH)的有效性评价结果。由此可知,在lognormal分布假设下三个模型均得到较优的评价结果。IID异质性和CAR异质性的空间PH模型均优于非空间的PH生存模型。三种参数假设下,IID异质性的空间PH模型的评价结果最好,且估计出的vi的方差十分显著,其中lognormal分布(最优)假设下估计出vi方差的95%置信区间为(0.062 3,0.713 5),显著不等于0,即认为各省份债务风险之间存在解释变量以外的空间异质性。相比较于IID异质性的空间PH模型,CAR异质性的空间PH模型评价结果略逊一筹。由于本文在考虑风险因素时,已经将相邻区域GDP作为重要解释变量放在模型中,因此地方政府个体异质项中的空间关联相对微弱。

表5 PH模型与SPH模型的有效性比较
表6列出了lognormal分布假设下三个模型的回归结果。由于事务分权与财政分权高度线性相关,故下文的回归模型中仅考虑财政分权(PerIncome)。从回归结果的整体上来看,仅土地出让金对数(lnlrr)的符号发生了变化,其余解释变量不仅符号一致,系数大小也相差不大。
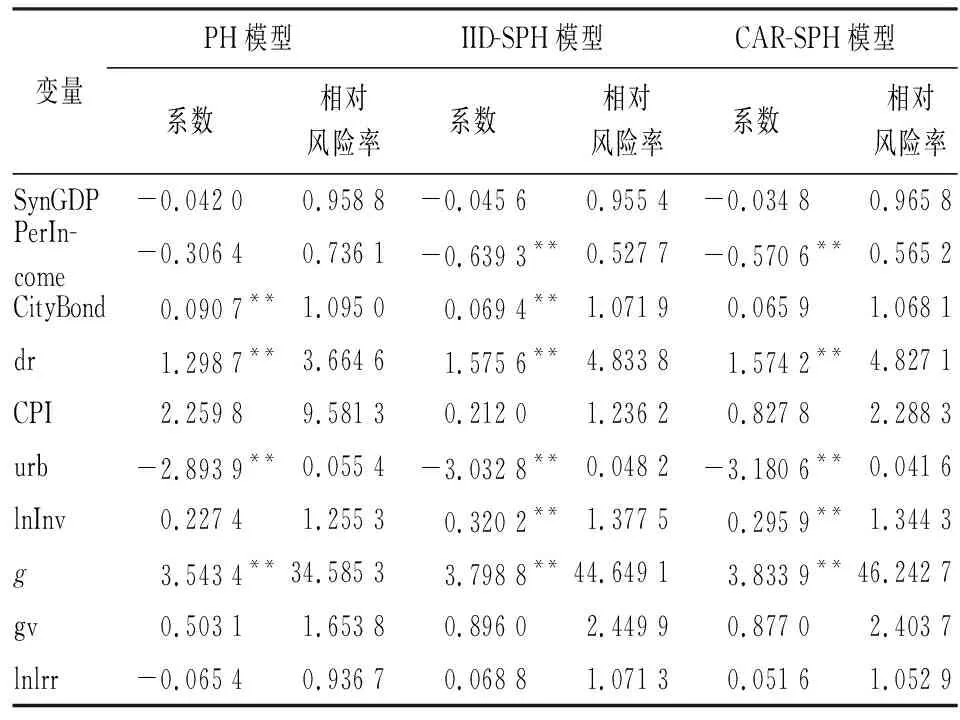
表6 lognormal分布的PH模型与SPH模型的回归结果
从IID个体异质性的空间PH模型(最优)的回归结果可以看出,财政分权的系数为-0.639 3,对应的相对风险率为0.527 7,且在95%的置信水平上显著。财政分权程度的加大对地方政府生存时间有显著的正向影响。虽然现有研究中部分学者认为本省份政府自主决定财政收支的权力越大,本省的债务水平越高[11]。但是,从另一个角度来说,财政分权自由度会加大地方政府对省内产业的扶持力度,有助于促进省内产业发展,增加可偿债收入,有利于地方政府的持续生存。
借款融资利率的系数为0.069 4,对应的相对风险率为1.071 9,且在95%的置信水平上显著。这说明在其他不变的前提下,借款融资利率每增加一单位,地方政府违约的风险增加9.5%。该结果与本文的假设保持一致,说明限定其他条件下,借款融资利率的提高会增加地方政府的短期偿债压力,缩短地方政府的生存时间。
债务负担率的系数为1.575 6,对应的相对风险率为4.833 8,且在95%的置信水平上显著。与前文假设一致,说明债务负担率的增加减少了地方政府的生存时间。债务负担率代表地方政府的债务存量,不仅短期内需要偿还债务产生的利息,长期还本付息的压力对于地方政府来说是较大的生存风险。
现有研究普遍认为,城镇化建设耗费地方政府巨大财力支持的同时扩大了地方政府的债务规模[12]。而本文的回归结果中城镇化率的系数为-3.032 8,对地方政府的持续期有显著的正向影响,说明城镇化率的提高会同时促进经济水平的提升和税收水平的增加,长期来看,有利于地方政府的持续生存。
固定资产投资对数的回归系数为0.320 2,对地方政府生存期有显著的负向影响。地方政府举债主要是为了支援基础设施投资,因此固定资产投资会增加地方政府债务规模,不利于地方政府的持续发展。
人均GDP增长率的系数为3.789 9,在95%的置信水平下是显著的。这表明,经济发展速度较快地区的政府债务违约率高于经济发展速度较低的地区,在一个增长主要靠投资拉动的经济体里,经济发展水平更强的地区面临更大的债务风险,地方政府存在靠债务促增长的体制性冲动,经济发展水平越高的地区借债融资越多,长期来看,并不利于地方政府的持续发展。
(五)稳健性检验
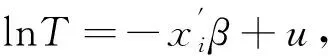
(18)
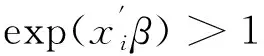
AFT模型也是半参数模型,表7分别列出log logistic分布、lognormal分布和Weibull分布形态下非空间AFT生存模型、IID异质项的空间AFT模型(IID-SAFT)和CAR异质项的空间AFT模型(CAR-SAFT)对应的LPML值、DIC值和WAIC值。从评价结果来看,空间AFT模型(IID异质项和CAR异质项)均优于非空间AFT生存模型。根据选择标准,三个模型中拟合程度最好的分布形态分别是Weibull分布、Weibull分布和lognormal分布。因此,选择对应三个分布对前面的分析做稳健性检验。
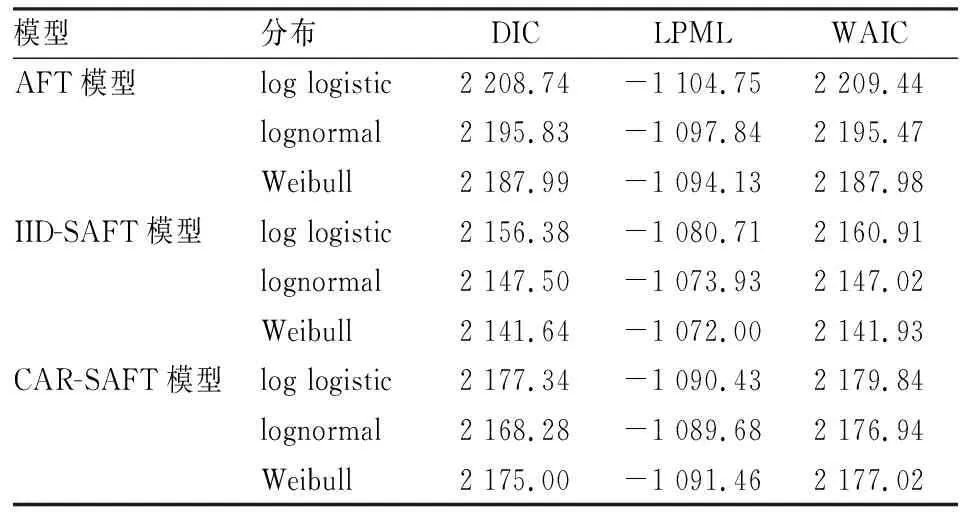
表7 AFT模型与SAFT模型的有效性结果
表8给出上述三个模型的回归结果。AFT模型直接对生存时间建模,在本文的模型设定中,符号为正的参数表示该解释变量会减少生存时间,增加违约风险,即x增加一单位将导致新生存时间为原来的e-β倍。
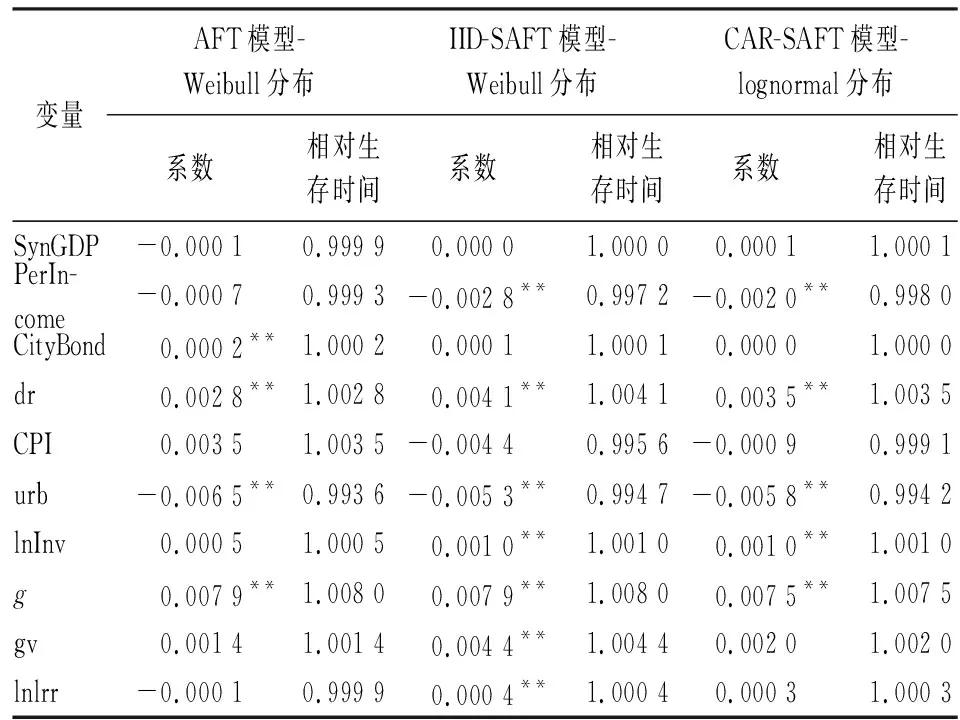
表8 AFT模型与SAFT模型的回归结果
对比表6和表8结果发现,95%置信水平下,对地方政府持续期起正向促进的因素有财政分权(PerIncome)和城镇化率(urb);对地方政府持续期有负向影响的因素有债务负担率(dr)、固定资产投资对数(lnInv)和人均GDP增长率(g)。所得到的结果与前文PH模型的回归结果基本一致,表明前文的分析结果是稳健的。
五、结 论
本文在区域经济异质关联框架中,从理论角度证明地方政府债务存在空间关联性,并利用空间生存分析模型对影响地方政府持续期的各种因素进行检验。空间生存模型克服了中国地方政府债务数据短、数据删失多等困难,可计算出各地方政府在未来各时点的违约概率。
研究结果显示:首先,不考虑地方政府主观上不愿意偿还和政府的预算软约束现象,仅从地方政府的偿还能力出发的研究结果表明,中国地方政府自2010年起不发生债务违约的概率已降至3.57%。这一结果也表明,地方政府以往举债不加控制及中国地方政府债务管理体系严重缺乏。其次,各省级地方政府的债务风险在空间上存在个体异质性。DIC、WAIC和LPML准则显示IID个体异质的空间比例风险模型(IID-SPH)为最优模型,对将来时间地方政府的债务危机的发生可能性有较准确的预测,且模型结论具备较好的稳健性,可以用来对地方政府债务持续期进行预测。最后,最优空间生存分析模型显示,排除个体异质项的影响后,财政分权程度和城镇化率的提高增加了地方政府生存概率,有利于地方政府持续生存;借款融资利率、债务负担率、固定资产投资和人均GDP增长率的增加不利于地方政府的持续生存。

