采油单螺杆泵转子偏心率对碰摩系统的响应研究

李大奇 杨令仪 祖海英 魏雪彤 魏玉芬

（东北石油大学机械科学与工程学院）

采油单螺杆泵是油田中重要的采油设备。 单螺杆泵凭借对介质的适应性强、流量平稳、压力脉动小及自吸能力强等优点，广泛应用于油田中［1］。但是，单螺杆泵在高转速工作情况下存在运行不平稳的问题，这就需要对单螺杆泵的转子动力学进行研究。 针对采油螺杆泵振动问题，张越等对地面驱动螺杆泵的抽油杆柱能耗制动进行分析，得出高阶固有频率对杆柱自由端振动影响较小，并给出杆柱受外力载荷时的主振动方程［2］；许蕾对地面驱动单螺杆泵工况预测工作进行了数学模型的建立，解决了工作过程中相关工艺参数的预报问题［3］；吕彦平等建立了单螺杆泵采油系统启动扭矩动力学模型，并取得良好的现场使用效果，为提高螺杆泵采油系统效率和工况诊断提供了理论基础［4］；廖金军等根据工业现场螺杆泵异常振动情况进行分析，给出了从确定原因到消除异常工况的办法［5］。 根据当前转子动力学方向的研究进展，侯兰兰和向玲建立碰摩力作用下参数不确定转子系统的动力学模型，得出偏心量取中等值时系统的运行状态最复杂［6］；赵道利等分析了混合偏心对不平衡磁拉力作用下偏心转子-轴承系统振动特性影响， 得出净偏心量与转子重力夹角值越大系统越趋于稳定［7］；徐学平等通过建立不平衡磁拉力、静载荷、不平衡质量共同作用下转子系统运动微分方程，分析得出净偏心方向影响轴心轨迹的位置分布，且净偏心量过大会加剧振动［8］；花纯利等在对转子-橡胶轴承系统的分析研究中，首次考虑橡胶轴承的非线性，建立了转子碰摩系统动力学模型，并分析了系统参数对转子系统动力学行为的影响［9］；何鹏等推导出考虑转子轴向温度分布的有限元模型， 体现转子轴向温度分布对刚度矩阵的影响，提高高温工作转子临界转速计算精度［10］。 当前国内外对采油螺杆泵振动方向的研究多集中于抽油杆柱的振动和泵体外部振动，因采油单螺杆泵定转子相对运动形式的特殊性，尚没有针对采油单螺杆泵转子系统动力学方向的研究，因采油单螺杆泵实际工作过程中需要反复进行转子相对定子的半圆周纯滚动和直线运动，笔者针对定子橡胶发生溶胀之前定转子之间尚有预留间隙，采油单螺杆泵转子相对定子进行圆周运动阶段，将1/4导程的运动简化在一个单截面内建立转子系统动力学模型，利用数值积分的方法求解并进行动力学响应特性的分析。 研究了转速、偏心率对转子碰摩系统响应特性的影响。

1 圆周运动阶段理论模型的建立

采油单螺杆泵在采油之前，金属转子与橡胶定子之间具有一定的预留间隙，在采油工作开始后定子橡胶会随时间变化，逐渐发生溶胀现象使定转子之间配合方式变化为过盈配合。 笔者针对定子发生溶胀现象之前，转子沿着右侧半圆路径做纯滚动的情况进行建模分析。 根据其工作原理将进行圆周运动的1/4导程的转子等效在一个单截面内进行力学分析并建立动力学模型，简化后的模型如图1所示。

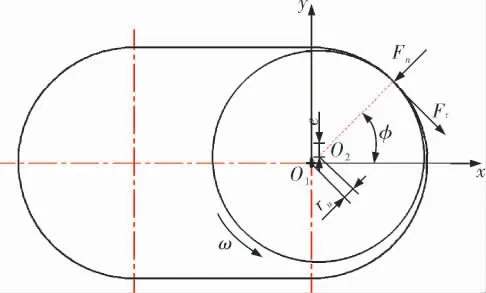
图1 转子受力情况

根据对丁腈橡胶在20℃水浸工况下静刚度实验的实验结果， 拟合出正常工况下特定压缩量转子和定子之间接触力模型；摩擦力模型采用Andersson修正的摩擦模型［11］；转子受力表达式为：

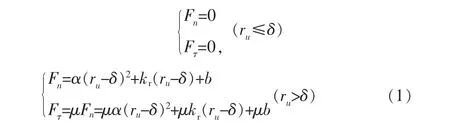
建立转子系统动力学方程如下：

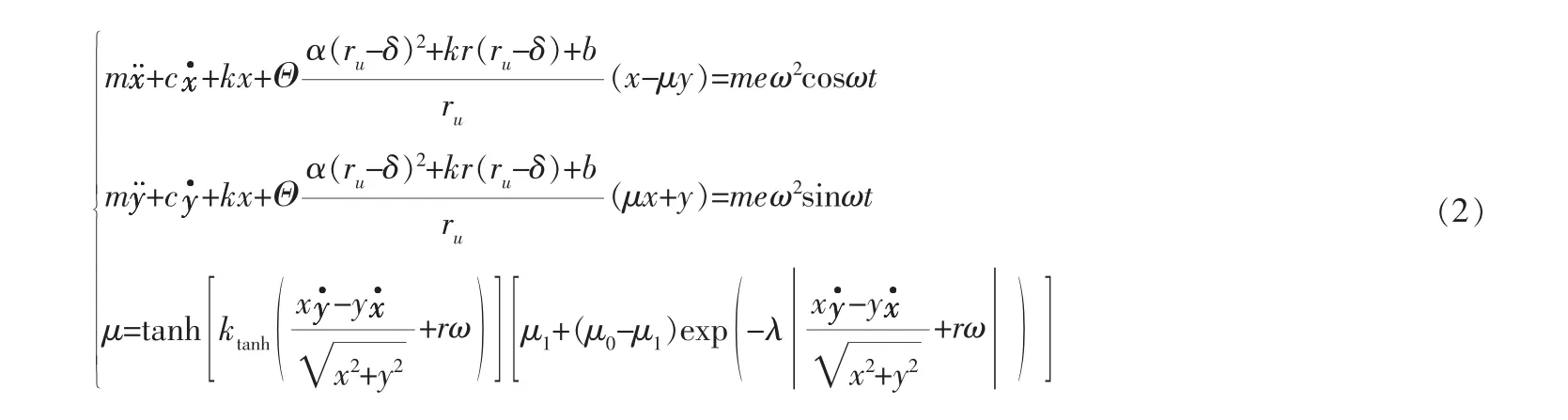
式中 c——阻尼；

e——转子质心与几何中心之间的距离；

k——转子刚度；

kr——定子内环面线性刚度；

ktanh——决定函数tanh变化快慢的系数；

m——一个导程转子质量；

r——转子半径；

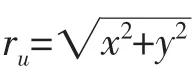
δ——定转子之间的预留间隙；

Θ——Heaveside函数， 根据转子径向位移ru与定转子预留间隙δ间的关系，取0或1；

μ——定转子之间的摩擦系数；

μ0——静摩擦系数；

μ1——库仑摩擦系数；

ω——转子角速度；

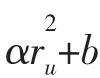
将方程（2）去量纲可得：

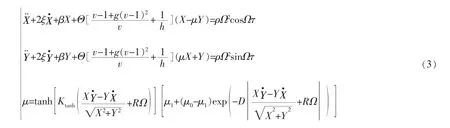
D=λδω0，Ktanh=δω0ktanh。

2 数值求解分析

对量纲处理后的式（3）利用定步长四阶龙格库塔法求取数值解， 为能获取稳定的数值解，积分计算2 000个周期并选取后200个周期的结果进行理论分析，得到该系统的动力学响应图。 各系统参数数值为：ξ=0.078，β=0.19，g=5.6，μ0=0.3，μ1=0.1，ρ （1，2，3，4，5，6，7） =（0.3，0.4，0.5，0.6，0.7，1.0，1.5）。

以图2为例详细分析转子在偏心率ρ=0.4时的运动特性。如图2a所示，随着转速比Ω增加到0.247时，进行无碰摩周期运动的金属转子与橡胶定子发生第1次碰摩， 运动状态过渡为周期全周碰摩运动，如图2b所示，轴心轨迹是一个规则的圆形，转子运动幅值达到0.18，频谱图中有一条谱线，庞加莱截面图上有一个点，表明此时转子做单周期运动；Ω=0.410时转子振幅达到最大（图2c），与此同时定转子间相对运动形式由全周碰摩运动向局部碰摩过渡，此时在转子的运动过程中会与定子发生一次或数次的碰撞；Ω=0.670到Ω=0.800区间内发生跳跃现象， 振幅由0.643 2逐渐减少到0.548 2， 并且转子在此区间进行全周碰摩运动，如图2d所示，转子的轴心轨迹为振幅0.548 2的规则圆形，庞加莱截面图上只有一个点；随着转速比继续增加到Ω=1.210之后， 系统由局部碰摩进入到混沌状态，转子发生无规则运动，如图2e所示（Ω=1.300），转子轴心轨迹图为连续的混乱的反复运动的线条，相图上为细密、无规则的图形，频谱图中也由于多摩擦引起了多频率现象，此时转子的运动状态反映到庞加莱截面图上为一系列杂乱无章的点，说明此时转子正处于运动状态不可预测的混沌状态。

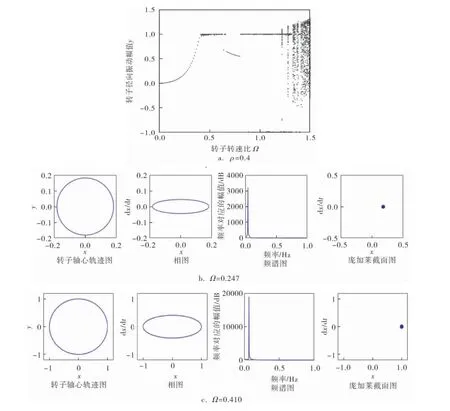
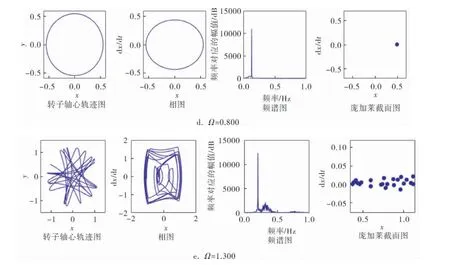
图2 ρ=0.4时转速比对转子系统响应的影响

考虑偏心率对转子系统的影响（图3），偏心率ρ=0.3时（图3a），随着转速比Ω的增加，在转速比Ω=0.271时，定转子发生碰摩，此时转子相对定子开始进行同频全周碰摩运动； 当转速比继续增加到Ω=0.450时，转子振幅达到最大值0.851 7；并且在转速比继续增加时转子振幅逐渐减小到接近0.3； 当转子从高转速降速时，转子振幅逐渐增加，在降速到转速比Ω=0.450时转子振幅达到最大，继续降速时转子振幅逐渐减小，且降低到Ω＜0.271时，转子与定子分离， 从同频全周碰摩转变为无碰摩周期运动；偏心率ρ=0.6时（图3c），随着转速比增加到Ω=0.211时， 转子从无碰摩周期运动转变为单周期全周碰摩运动，且继续增加到Ω=0.380时，全周碰摩运动振动幅度达到最大值， 随后转子进行局部碰摩运动， 当转速比持续增加到Ω=1.160以上时，转子运动进入混沌状态；偏心率ρ=1.0时（图3e），Ω=0.172时转子从无碰摩周期运动过渡为同频全周碰摩运动，并随转速比的增加继续增加振动幅度，Ω=0.330时转子振动幅度达到最大值0.998 8，转子仍进行同频全周碰摩运动，Ω=0.500时转子处于局部碰摩运动状态，Ω＞1.010时，系统进入混沌运动，Ω=1.290时，随着旋转速度的继续增加，由于定转子局部碰摩运动不断加剧， 最终导致系统反向全周碰摩运动的出现，此时系统的响应幅值急剧增加，出现这种状况时系统将无法正常工作； 偏心率ρ=1.5时（图3f），Ω=0.143时转子开始进行同频全周碰摩运动，Ω=0.290时转子在同频全周碰摩运动阶段振幅达到峰值，Ω=0.390时发生局部碰摩，Ω=0.910时系统进入混沌状态，Ω=1.140时系统进行反向全周碰摩运动， 在实际工况下应极力避免这种情况的发生。

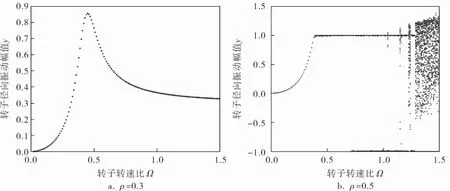
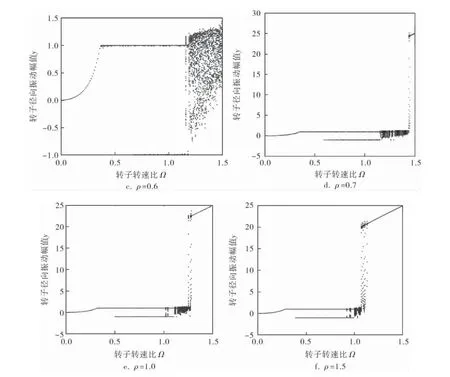
图3 偏心率对转子系统的影响

3 结束语

根据采油单螺杆泵工作原理将1/4导程进行圆周运动的转子等效在一个单截面内进行分析，建立动力学模型，并利用定步长四阶龙格库塔法进行数值模拟，通过分析得到螺杆泵转子受偏心率影响的动力学响应规律：偏心率ρ＜0.3时，系统进行无碰摩和同频全周碰摩两种形式，不会发生混沌现象，偏心率增加转子振幅峰值增加；0.4＜ρ＜0.6时，转子振幅峰值达到最大值，系统随转速比增加会出现混沌现象；偏心率ρ＞0.7时，随转速比增加，系统会出现反向失稳现象，适当降低偏心率能够减缓系统的振动，避免混沌和反向失稳现象的发生。