河北省冬小麦返青期预测模型研究

单琨 杨帅 罗晶 李茜

摘要：利用河北省11个农业气象观测站1981-2018年农业气象、地面气象观测资料，基于线性回归和灰色系统模型GM（1，1）构建冬小麦返青期预测模型，并对模型模拟效果进行评估。结果表明，各站冬小麦返青期线性趋势模拟曲线不显著。用灰色系统模型G（1，1）模拟各站冬小麦返青期，11个站点中有10个站点模拟精度在二级及以上。通过分析积温序列与冬小麦返青期的相关性，确定10月1日至次年2月15日的负积温为冬小麦返青期关键影响因子。各站点综合冬小麦返青期序列与关键时期负积温一元线性回归方程极显著。单站线性趋势模型、灰色系统模型GM（1，1）模拟和以负积温为因变量的各站点综合线性回归模拟冬小麦返青期检验绝对误差小于7d的概率分别为73%、94%和80%。单站数据变化比较平稳的条件下，冬小麦返青期预测可根据灰色系统模型GM（1，1）来构建;单站数据存在突变式波动时，可用线性方程构建预测模型;在气候变化波动较大的背景下，基于各站点综合数据序列的线性回归方程，用关键时期负积温来预测冬小麦的返青期适用于区域分析。

关键词：冬小麦返青期;线性回归;灰色系统模型GM（1，1）;河北省

中图分类号：S512.1

文献标识码：A

文章编号：0439-8114[ 2020）12-0022-05

DOl：10.1408 8/j .cnki.issn0439-8114.2020.12.005

开放科学（资源服务）标识码（OSID）：

返青指的是早春麦田50%以上的麦苗心叶（春生一叶）长出部分达到1-2 cm。这个时期的生长主要是生根、长叶和分蘖。小麦返青期是促使晚弱苗升级、控制旺苗徒长、调节群体大小和决定成穗率高低的关键时期，对后期小麦能否高产起到重要作用。小麦返青期的水肥管理越及时效果越好，同时浇水、施肥和防治病虫害等操作都与天气变化有密切联系。当前关于小麦返青期研究主要是返青期田间管理、水分管理方面的研究[1-5]，小麦返青期冠层、营养物质等方面的研究[6，7]。气象指标与返青期的分析主要集中在生育期气象指标和气候变化对生育期的影响两个方面[8-14]，关于气象观测资料与小麦返青期的研究很少。

在预测模型中，常用的是系统的两个特征参数变化和分布呈接近线性的关系，对于这样的模型，一般是采用一元线性回归的方法，在气象数据分析中比较常用[15，16]。灰色系统理论把客观对象视为一个灰色的物质系统，在研究系统时，通过系统的表征信息，利用关联分析、灰数生成、灰色建模等信息加工手段，探求系统内在的規律，预测系统未来的发展状态。灰色预测就是运用灰色系统理论，通过灰色建模来对系统特征参数变化进行预测的一种实用方法[17-19]。本研究基于地面气象资料和农业气象观测资料，以河北省为研究对象，基于线性回归方程和灰色系统模型CM（1，1）分析研究小麦返青期的预测模型，并对模型模拟效果进行评估，以期为这方面研究提供参考。

1 材料与方法

1.1 资料

基于数据质量和观测项目选用河北省11个农业气象观测站（图1）1981-2018年农业气象观测资料和地面气象观测资料。

1.2分析方法

1.2.1信息扩散法为了能够准确地建立影响因子与小麦返青期波动之间的关系，采用信息扩散法对数据进行膨化处理，得到多个连续时段的变量数据，根据相关系数确定影响的关键期。

假设作物的全生育期为n天，某个因子变量定义为X，则单位因子为Xi（i=1，2，3……，n），膨化单元为k（k=2，3，……，n），膨化公式如下式：

1.2.2 灰色模型GM（1，1）灰色模型CM（1，1），灰色系统理论是基于关联空间、光滑离散函数等概念定义灰导数与灰微分方程，进而用离散数据列建立微分方程形式的动态模型，即灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且较有规律的生成数，建立起微分方程形式的模型，这样便于对其变化过程进行研究和描述。设变量X（0）=

1.2.3 线性回归 经过相关分析后进行线性回归分析，回归方程为：

Y=β1+β2X+u

（8）

式中，y为因变量，X为自变量，β1为截距，β2为斜率，u为随机误差。

2 结果与分析

2.1 河北省冬小麦返青期分析

河北省冬小麦返青期在2月2日-3月25日。为了方便比较，将冬小麦返青期进行数值化处理，从2月1日开始，记为1，逐日累加，如返青期为2月15日，数值化后为15。

河北省各站点冬小麦返青期年际变化见图2。由于单站数据序列长度有限，各站点冬小麦返青期线性趋势不显著。8个站点冬小麦返青期呈延后趋势，但存在区域差异，中部地区（河间站、霸州站）冬小麦返青期年际变化曲线变化率较大，延后趋势明显;东南部3个站点黄骅、阜城、深州冬小麦返青期年际变化率为负，返青期呈提前趋势。20世纪初黄骅、阜城、深州3个站点冬小麦返青期出现大幅度提前的波动，致使趋势线向下倾斜，这可能与区域气候突变有关。

2.2冬小麦返青期灰色系统模型GM（1，1）分析

构建河北省各站点冬小麦返青期的灰色系统模型GM（1，1）。与线性趋势线比较（图2），东南部3个站点（黄骅、阜城、深州）中，黄骅站点的返青期模拟曲线呈增长趋势（图3），与线性趋势线差别较大，这可能因为此站点返青期年代间波动较大，不同模拟计算方法对数据处理的差别较明显;其他站点虽然均呈增长趋势，但是增长幅度与线性趋势模拟的结果同样存在差异，尤其是霸州站，线性趋势线与变化趋势的拟合度明显好于灰色系统模型CM（1，1）模拟曲线，而霸州站的返青期年代变化波动同样很大。由此可见，当返青期年代变化波动较大时，线性模拟曲线与数据变化曲线拟合性更好些。

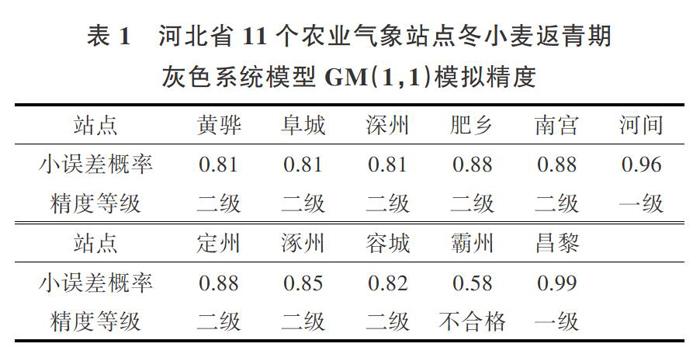
河北省各站点冬小麦返青期灰色系统模型GM（1，1）模拟精度分析表明（表1），东南部地区黄骅、阜城、深州3个站点模拟精度为二级;中部地区河间、定州、涿州、霸州4个站点中有3个站点模拟精度为二级及以上，1个站点为不合格;北部的昌黎站模拟精度最高。用灰色系统模型GM（1，1）模拟各站点冬小麦返青期，11个站点中有10个站点模拟精度在二级及以上。灰色系统模型CM（1，1）对年际波动均匀、突变少的数据模拟精度很高，如昌黎站的冬小麦返青期;但是对有断崖式突变的数据序列模拟精度较差，如霸州站的冬小麦返青期。

2.3 温度与冬小麦返青期的相关分析

溫度是影响返青期的关键影响因子，为了更好地模拟返青期，分析温度与返青期的关系，用信息扩散方法对温度数据进行处理，从10月1日开始，以10 d为最小膨胀单元，分别计算得到平均温度积温、正积温、负积温的膨化数据序列。通过分析积温序列与冬小麦返青期的相关性，确定关键影响因子为10月1日至次年2月15日的负积温（后文简称“负积温”）。

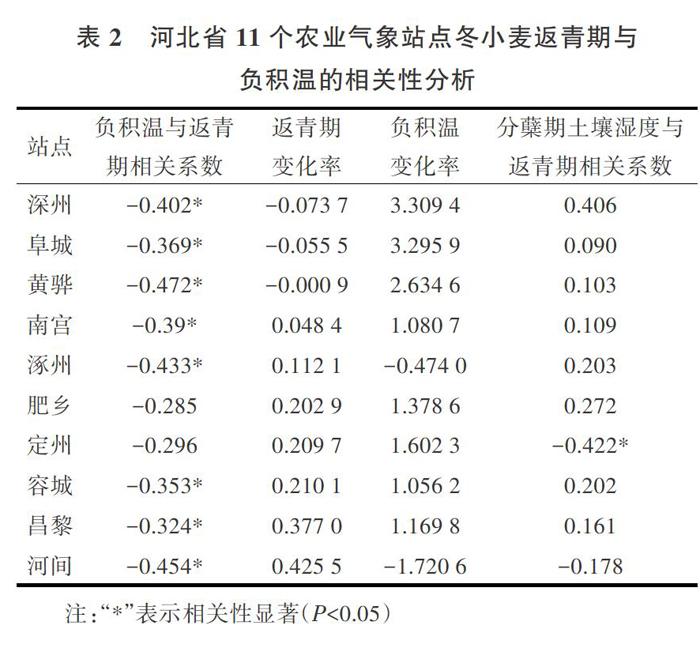
对负积温和冬小麦返青期进行分析（表2），河北省11个农业气象站点中9个站点负积温与冬小麦返青期的相关性显著;负积温变化率与气候变暖趋势基本一致，80%以上站点负积温变化率为正，只有肥乡和定州2个站点负积温与返青期相关性不显著。考虑到小麦返青期除了受到温度影响，也会受冬前土壤湿度的影响，分析分蘖期土壤湿度与冬小麦返青期的相关性（表2）发现，肥乡和定州2个站点相关系数绝对值较大，可能是这2个站点负积温与返青期相关系数不显著的原因。

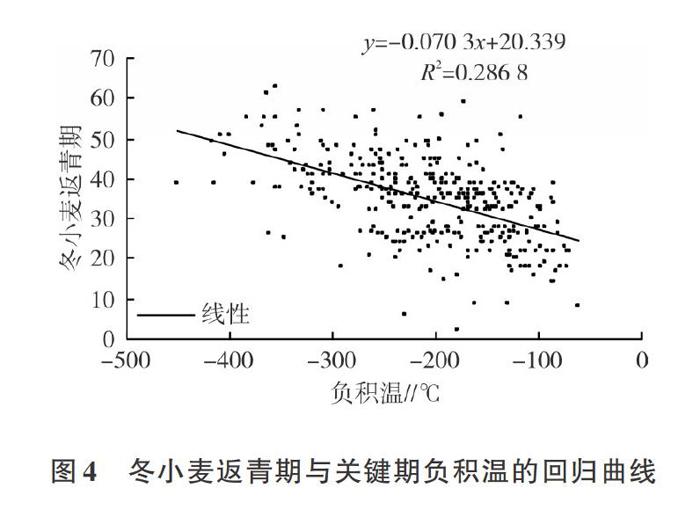
2.4 负积温与冬小麦返青期的回归分析

负积温与冬小麦返青期相关性很高，但是由于各农业气象站点数据序列长度为25-37，数据序列长度有限，单站线性回归分析达不到显著性，所以将所有站点数据合并成一个综合数据序列进行回归分析。冬小麦返青期与负积温的一元线性回归方程（F=107.325 6>3.871，F=8.09E-22<0.000 01）回归性达到了极显著水平（图4）。

2.5 模型检验

为了检验模型的预测效果，每个农业气象站点留取最后3年的数据不参与构建模型，用来检验模型的预测误差。由于单站线性趋势模拟曲线不显著，趋势线性预测检验平均绝对误差为4.8 d，最大误差为11d;灰色系统模型GM（1，1）预测检验的平均绝对误差为4.3 d，最大误差为12 d;以负积温为因变量的线性回归模型预测检验的平均绝对误差为4d，最大误差为10 d。单站点线性趋势模拟曲线预测检验绝对误差小于7d的概率为73%，灰色系统模型GM（1，1）预测检验绝对误差小于7d的概率为94%，以负积温为因变量的线性回归模型预测检验绝对误差小于7d的概率为80%。

3 小结与讨论

单站冬小麦返青期线性趋势模拟曲线不显著;根据灰色系统模型GM（1，1）模拟各农业气象站冬小麦返青期，11个站点中有10个站点模拟精度在二级及以上;通过分析积温序列与冬小麦返青期的相关性，确定10月1日至次年2月15日的负积温为冬小麦返青期关键影响因子，各站点综合冬小麦返青期序列与关键时期负积温一元线性回归方程达到极显著水平。根据11个站点冬小麦返青期年际变化特点和主要影响因素用线性模拟、灰色系统模型GM（1，1）、线性回归方法构建模型，都能较好地反映冬小麦返青期变化规律。

根据线性趋势模拟和灰色系统模型GM（1，1）构建的冬小麦返青期预测模型都是对单站数据的模拟，不需要加入影响因子，是单纯的对数据序列变化规律的模拟，二者的模拟精度稍逊于以负积温为因变量的线性回归模型，适合单站使用。灰色系统模型GM（1，1）预测检验绝对误差小于7d的概率为94%，明显优于线性趋势模拟（73%）。但是，如果数据序列存在断崖式突变，就会影响模拟效果（如霸州站），灰色系统模型CM（1，1）更适合数据突变比较平稳的数据序列，数据序列存在突变波动时用线性趋势模拟的方法更好些（如霸州站）。

利用历史值检验模型的预测精度，以负积温为因变量的线性回归模型预测平均绝对误差（4 d）和最大误差（10 d）最小，回归方程达到了显著水平。以负积温为因变量的线性回归模型，需要整合区域内所有站的数据，同时加入了因变量，从而增大了模型的拟合率。在数据有限的条件下，以负积温为因变量的线性回归模型比较适合区域冬小麦返青期预测模型的构建。在个别站点（如肥乡站）负积温与冬小麦返青期相关性不显著，而分蘖期的土壤湿度与返青期相关系数显著，如果有土壤湿度数据，可进一步丰富回归模拟性的因变量，提高预测准确性。

参考文献：

[1]李秀，史志梅.浅谈小麦返青拔节期管理[J].福建农业，2014.8（15）：28.

[2]任青，陈诚，翟斌豫南小麦返青期病虫草害综合防治[J]河南农业，2014（4）：35.

[3]张英奎.冬小麦春季管理技术[J-现代农村科技，2018（12）：24.

[4]佟国香，周吉红，毛思帅，等.返青期一次追施不同量的缓释尿素对小麦发育和产量的影响[J].农业科技通讯，2019（2）：58- 60

[5]李艳丽.小麦返青后主要病害及预防措施[J]种业导刊，2018（4）：23.

[6]李树强.冬小麦返青期冠层光谱特性分析[J].贵州农业科学，2014.42（2）：65-68.

[7]王芊，李存军，王大成，等，基于氮素和水分的冬小麦籽粒蛋白质含量监测[J].农业T程学报，2008，24（ S2）：22-24

[8]田家波.基于小麦全生育期气象条件精细化分析[J].安徽农业科学，2016，44（ 28）：183-185.

[9]刘畅.气候变化对京津冀冬小麦的影响研究[D]南京：南京信息工程大学，2014.

[10]林文.气候变化对陕西冬小麦影响研究[D].陕西杨凌：西北农林科技大学，2013.

[11]周伟，金梅，成军军，等.气候变暖对汾阳市冬小麦积温及生育期的影响[J].甘肃农业科技，2012（ 10）：19-20

[12]侯学会，隋学艳，姚慧敏，等中国北方麦区冬小麦物候期对气候变化的响应[J].麦类作物学报，2019，39（2）：201-209，

[13]马倩倩，贺勇，张梦婷，等中国北部冬麦区小麦生育期对生育阶段积温变化的响应[J].中国农业气象，2018，4（3）： 233- 244.

[14]周吉红，毛思帅，王俊英，等.北京地区小麦生育期温度演变及不同生育时期温度指标[J].作物杂志，2016（3）：116-122.

[15]张荣菊，李志梅，鄂温克族自治旗羊草返青期预报模型[J].内蒙古农业科技，2015，43（3）：132-134.

[16]李静，陈效逑，崔铁军.内蒙古草原返青期对气候变化的时空响应[J]天津师范大学学报（自然科学版），2017，37（2）：39-44

[17]靳力争，马洪英.白菜型油菜单株产量与相关性状的灰色关联度分析[J].长江蔬菜，2018（8）：50-52.

[18]黄彭，郝妙，杜永华，等基于CM（I，1）模型的四川粮食产量预测研究[J].农学学报，2017，7（10）：96-100.

[19]毛志，冉红林，基于灰色系统理论的铜仁市碧江区干旱预测研究[J]贵州工程应用技术学院学报，2018，3（36）：88-92.

作者简介：单琨（1984-），女，河北唐山人，硕士，工程师，主要从事农业气象和农业气象灾害风险分析研究，（电话）13403169717（电子信箱）tangshanshankun@126.com。