新型钢绞线拉索几何抗弯刚度试验研究

孙国军, 袁 军, 吴金志

(1.北京工业大学 建筑工程学院, 北京 100022; 2.北京工业大学 城市与工程安全减灾省部共建教育部重点实验室, 北京 100124)

近年来,索结构作为预应力空间结构的主要结构类型,在建筑结构中得到了日益广泛的应用.随着索结构的类型越来越丰富,以及人们对建筑美观和索构件防火要求的不断提高,许多新型钢拉索不断涌现.现有的钢丝类拉索根据材料可以分为钢丝绳、钢绞线和钢丝束.钢丝绳由绳芯、绳股和钢丝组成;钢绞线分为高钒钢拉索、不锈钢钢拉索和PE钢绞线等;按照JGJ 257—2012《索结构技术规程》,钢丝束分为平行钢丝束和半平行钢丝束.其中高钒索和不锈钢索这2种钢绞线类的钢拉索在预应力空间结构和幕墙中应用尤多.

由于高钒索和不锈钢索中钢丝存在绕捻特性,其几何抗弯刚度与普通钢构件存在较大差异.钢拉索抗弯刚度的主要决定参数是钢拉索的弹性模量和索体的截面惯性矩.钢拉索的弹性模量并不是一个确定值,而是一个非线性、与应力和时间有关的量,因而在实际工程中只能将该值确定在一个合理的范围内[1].一方面，在现场直接测量钢拉索的弹性模量比较困难；另一方面,钢拉索的截面惯性矩也并非一个稳定不变的数值,该数值与钢拉索的内部构造、钢丝之间绞捻形式、钢丝之间摩擦力大小等各种实际情况有关,其实际值介于各根钢丝惯性矩之和与按照钢拉索整体截面换算得到的惯性矩之间.但是在理论上,钢拉索制作完成后其抗弯刚度即为一固定不变的确定值[2].

Shimada[3]通过对钢拉索振动的高阶频率进行识别,提出钢拉索的抗弯刚度一般取0.5EI0左右;Roeck等[4]通过一系列的研究,最终认为钢拉索的实际抗弯刚度应取截面最大抗弯刚度的2/3;郑罡等[5]利用有限元模型,将频率测量值与计算值间的误差进行了处理,从而进行钢拉索抗弯刚度的识别;李宗凯[6]通过研究钢绞线自重作用下的挠度对钢拉索的抗弯刚度进行计算,并将其等效为面积相等的圆钢棒来估算索体的惯性矩,以此获得钢拉索的折算抗弯刚度;严琨等[7]通过对9根钢拉索进行静动力测试,发现悬索主缆的抗弯刚度接近按整体截面计算的抗弯刚度;李学有[8]采用最小二乘法对斜拉索的多阶实测频率进行分析,获得了斜拉索的抗弯刚度;苏成等[9]利用钢拉索的多阶频率,借助有限元法以及样条拟合技术来进行拉索抗弯刚度的识别,从而得到钢拉索的实际抗弯刚度;姚文斌等[10]利用三点弯曲原理,借助钢拉索拉力传感器测得钢拉索的索力,从而获得了钢拉索的抗弯刚度随索力变化的计算公式;武晓凤[2]通过对钢拉索进行有限元精细化分析以及试验研究,指出钢拉索的实际抗弯刚度介于最大抗弯刚度和最小抗弯刚度之间,该实际抗弯刚度值可以通过与钢拉索截面等面积的圆钢棒的抗弯刚度折减来表示,即钢拉索实际抗弯刚度为kE折算,其中k为折减系数,同时给出了不同条件下k的取值.

现有的钢拉索抗弯刚度研究大多是基于钢丝束来进行的.由于高钒索、不锈钢索与钢丝束的结构构造、捻角不同,因此它们的基本力学性能也不相同,已有的抗弯刚度计算公式对高钒索和不锈钢索已经不再适用.本文基于新型的高钒索和不锈钢索进行几何抗弯刚度试验,旨在提出适用于高钒索和不锈钢索的拉索抗弯刚度表达式,对高钒索和不锈钢索的实际工程应用起到一定的指导作用.

1 抗弯刚度识别方法

考虑拉索几何抗弯刚度,基于Bernoulli-Euler理论的梁理论,将索简化成承受轴力作用的梁模型,其振动微分方程为：

(1)

式中：m为索的线密度,kg/m;u(x,t)为索在t时刻x位置处的横向位移,m;T为索力,N;EI为索的抗弯刚度,N·m2.

根据文献[11],运用变量分离法求解式(1),最终得到一般边界条件下索的固有频率方程为：

Mtanh(βl)cos(αl)+Nsin(αl)+…+
Pcos(αl)+Qtanh(βl)+Rsech(βl)=0

(2)

式中：M、N、P、Q、R均为与拉索边界条件相关的系数;α为拉索几何抗弯刚度与全截面抗弯刚度的比值;l为拉索长度,m.

本文将索力作为已知量,拉索的抗弯刚度EI作为未知量求解,具体识别步骤如下：

当边界条件为铰接时,拉索索力的识别公式为：

(3)

当边界条件为固接时,拉索索力识别公式为：

(4)

由式(3)、(4)可以看出,不同边界条件下索力计算公式可以假设为相同的形式：

(5)

转换则可得：

(6)

式中：Hj为铰接时的拉索索力,N;fn为拉索的第n阶自振频率,Hz;n为自振频率阶数;Hf为固接时的拉索索力,N;H为拉索索力,N;a,b为计算参数.

在实际工程中,钢拉索的边界条件通常是介于铰接和固接之间的一种状态,因此假定索的边界为弹性嵌固[12].文献[13]将式(3)、(4)计算得到的索力取平均值作为估计值,带入铰接和固接时的索力识别公式中,得到此索力下铰接和固接时索的频率,再通过差值求得钢拉索索力.若两者的误差小于1%,则认为此时得到的钢拉索索力即为识别出的实际索力[14].

由于边界条件介于铰接和固接之间,首先采用两者的几何抗弯刚度识别公式的系数平均值作为识别拉索几何抗弯刚度EI的系数.由于本试验所用拉索长度较小,忽略垂度的影响,选择一阶频率来进行拉索几何抗弯刚度EI计算分析：

(7)

将1阶频率f1及其余参数代入式(7),得到几何抗弯刚度估算值EI0,再将EI0代入式(8)、(9),得到此索力和几何抗弯刚度下铰接和固接时索的频率f1j和f1f.

(8)

(9)

假定1阶频率f1所对应的索力为H1,f1j和f1f对应的索力分别为Hj和Hf,利用线性插入法得到：

(10)

(11)

(12)

2 高钒索和不锈钢索试验

2.1 试验构件

试验用拉索构件(见图1)为广东坚朗有限公司实际工程生产的直径为14、20、26mm的高钒索和不锈钢索,截面分别由1mm×19mm、1mm×37mm与1mm×61mm的钢丝绕捻而成.图中Galfan cable 1×19-14-2.9表示高钒索由单股钢绞线构成,截面共19根钢丝绕捻而成,索直径为14mm,钢丝直径为2.9mm,其余以此类推.

图1 试验用拉索构件Fig.1 Cables used in the experiment

试验构件分别处于3种预应力工况：7kN、0.3Fu和0.5Fu(Fu为钢拉索的最小破断力值),对每个试验构件均记录试验时具体加载的索力值.试验涉及的各个钢拉索的弹性模量取拉力试验测得的钢拉索的实际弹性模量E,试验用拉索构件的具体参数和实际弹性模量取值见表1.

2.2 试验加载测试装置

试验反力设备为自制反力钢架,如图2所示.试验过程中利用千斤顶为钢拉索构件施加预应力,拉索端头处用螺栓与钢架进行固定,同时采用JMZX-3003综合测试仪监测钢拉索的实际索力,以保证试验全过程的预应力始终保持在设计值.在拉索全长范围内均匀布置5个竖向加速度传感器,利用Imc数据采集仪对钢拉索进行加速度信号采集.

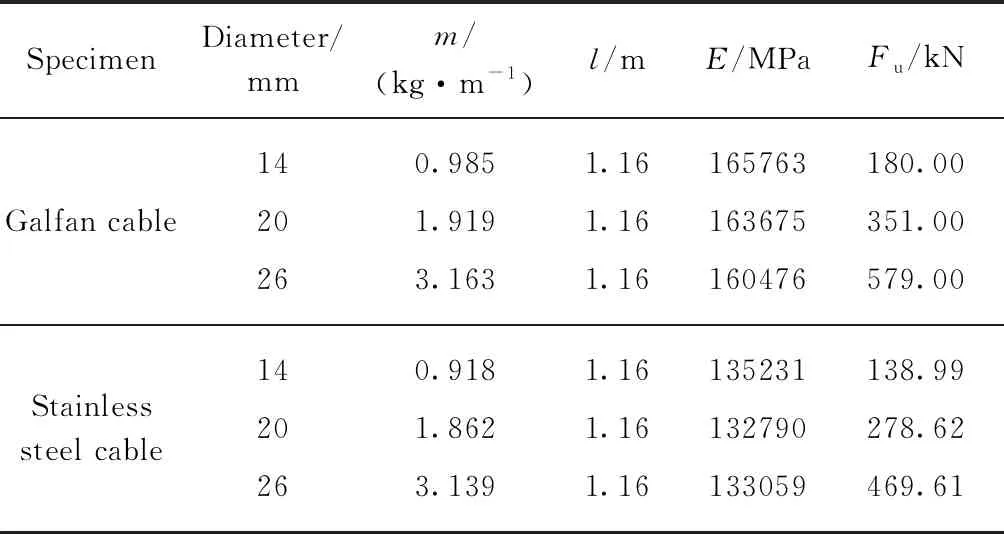
表1 试验用拉索构件参数

试验开始前,首先对试验构件进行超张拉处理,消除索体钢绞线之间的缝隙对试验结果的影响;然后通过拉力试验机,使用力控制加载模式,以10MPa/s的速率匀速加载到0.5Fu后,再匀速卸载使力降至5kN;重复3次,完成钢拉索试验前的超张拉过程.

图2 试验设备Fig.2 Experimental equipment

2.3 试验方法

试验方法采用锤击法和自由振动(环境激励)2种.锤击法利用橡皮锤对构件施加外部激励,自由振动法为在安静的环境条件下让其自由振动,从而分别测得其加速度信号,利用频率响应分析FDD方法,采用Matlab编程对5个加速度传感器的信号进行处理,从而得到该构件的各阶固有频率.通过预处理发现,由于锤击法力度较大,导致加速度传感器在测量过程中位移较大,加速度值测量偏差较大,因此选用自由振动(环境激励)方式测得的加速度信号进行数据处理.

为了尽可能消除试验误差,各型号试验构件均取用2根相同直径的钢拉索,且每根钢拉索进行5

组重复试验,最终测得10组加速度信号值,再通过这10组加速度信号计算得到10组频率值,最终取10组频率值的平均值作为钢拉索的试验频率值.

2.4 试验结果

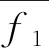
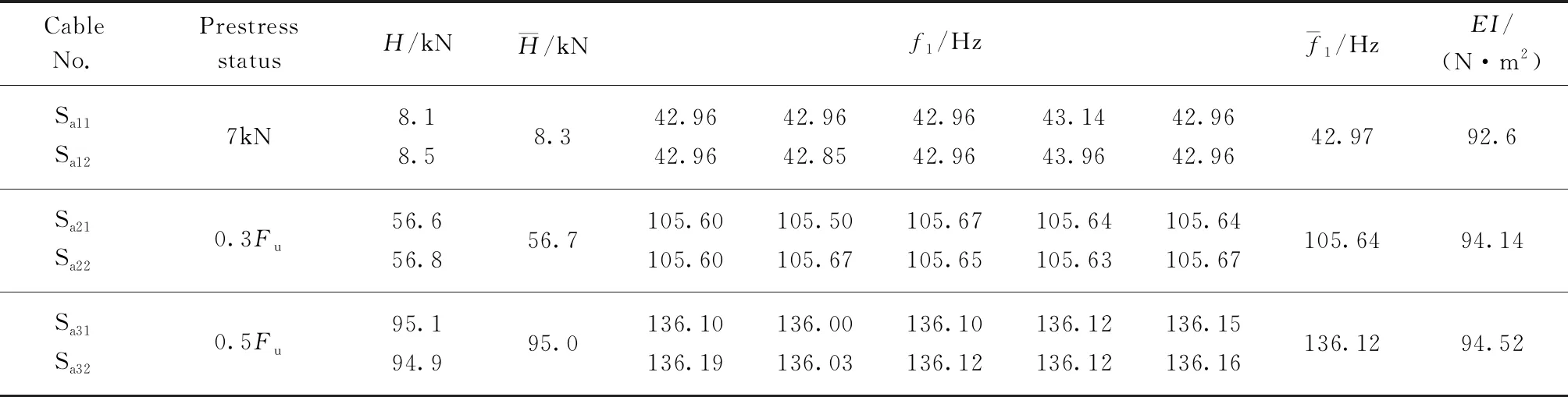
表2 高钒索1×19-14-2.9抗弯刚度

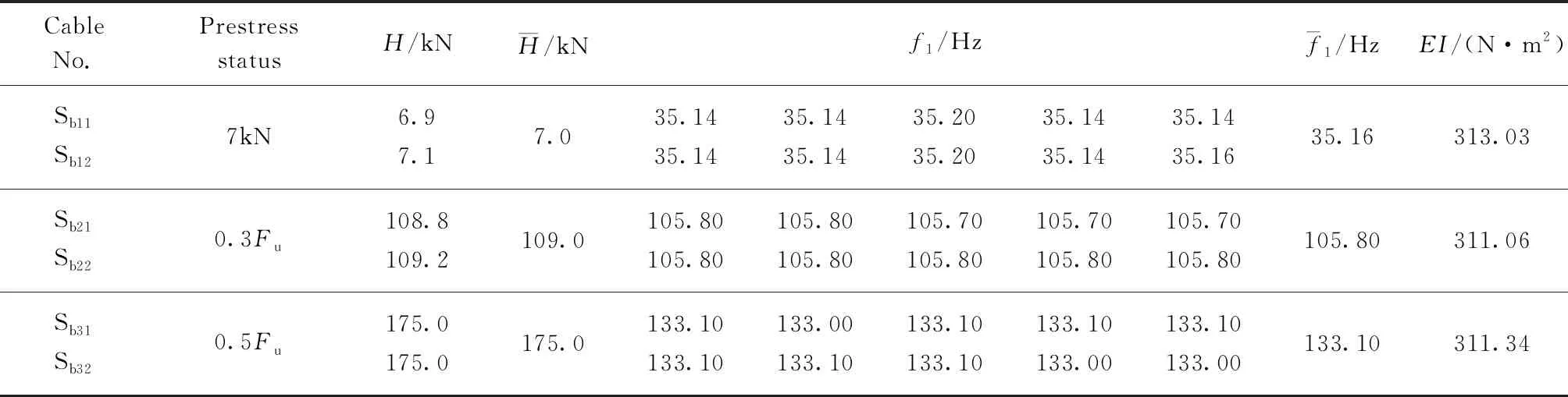
表3 高钒索1×37-20-3.2抗弯刚度值

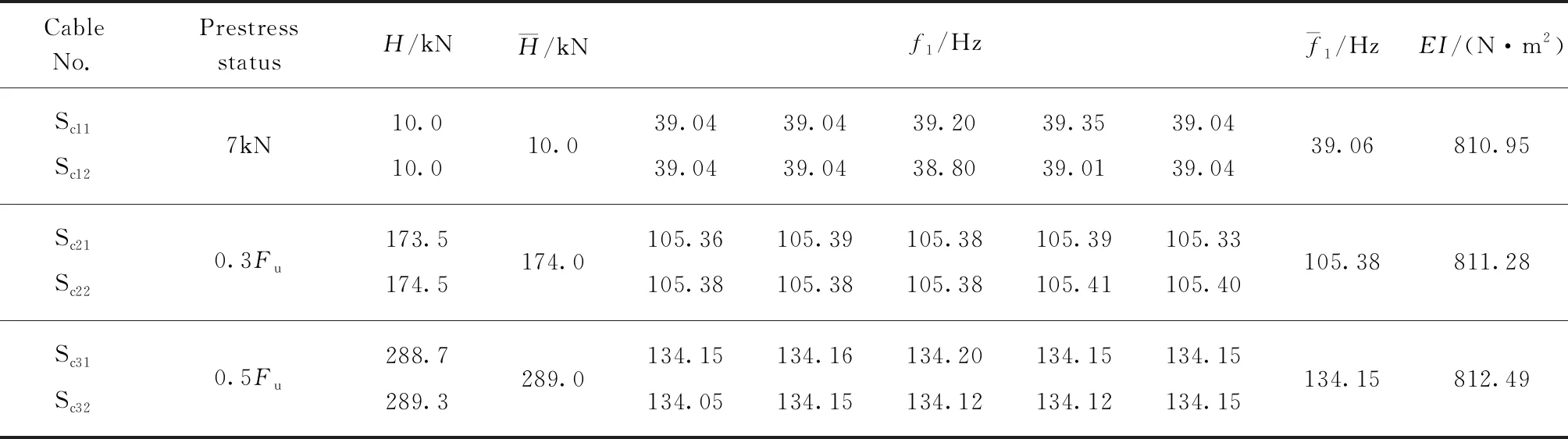
表4 高钒索1×61-26-2.9抗弯刚度

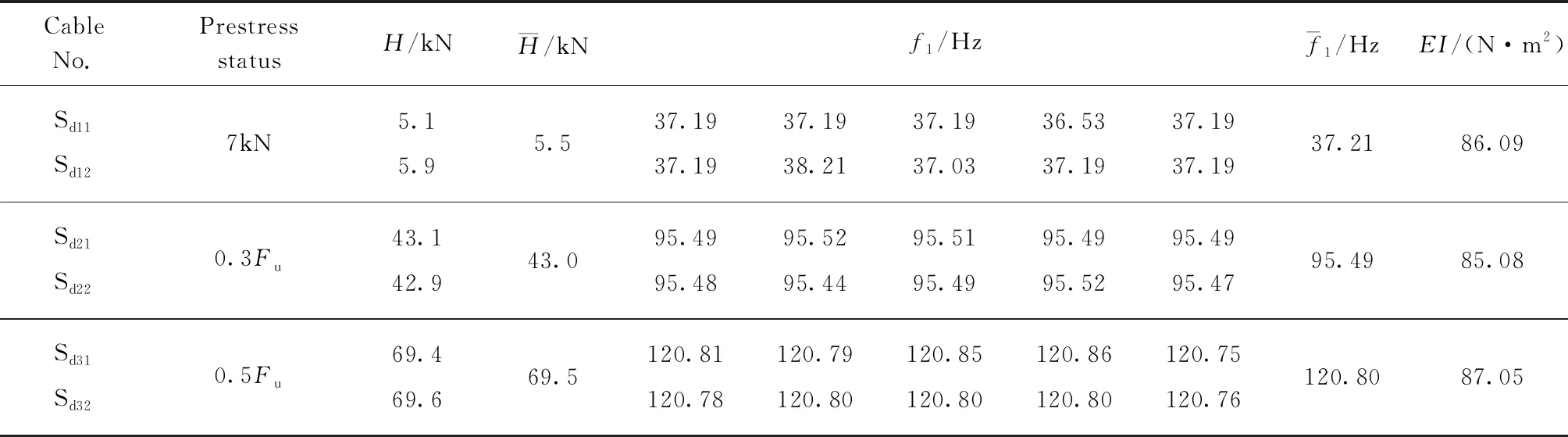
表5 不锈钢索1×19-14-2.9抗弯刚度

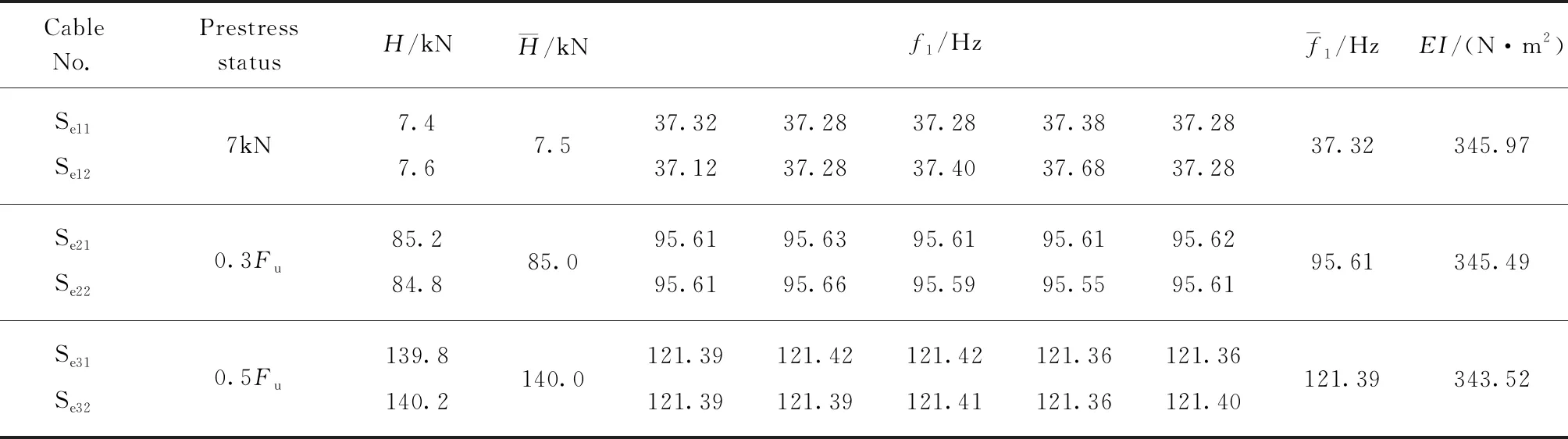
表6 不锈钢索1×37-20-3.2抗弯刚度

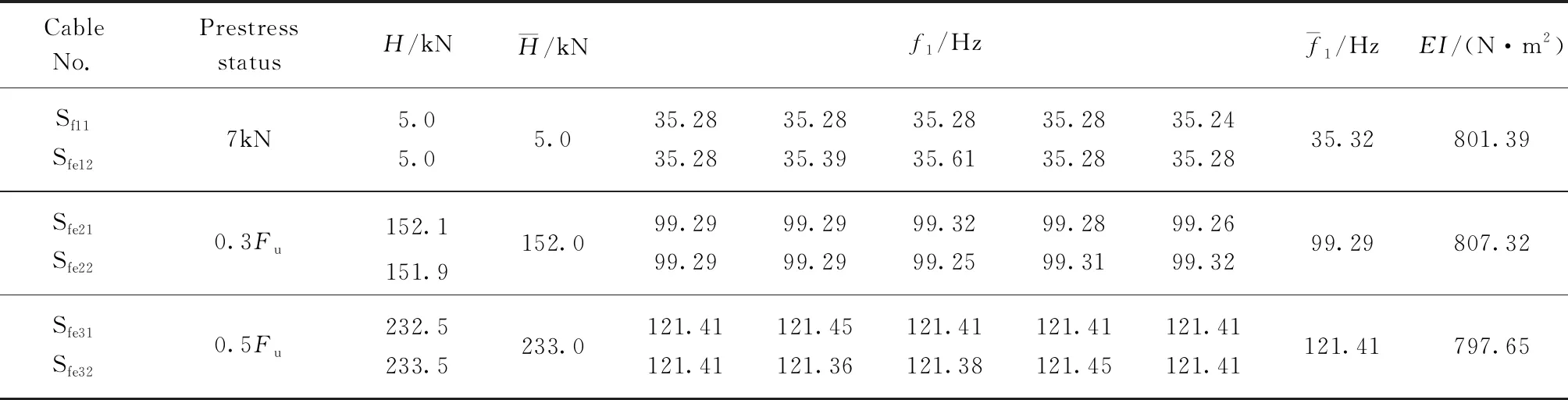
表7 不锈钢索1×61-26-2.9抗弯刚度

表8 拉索抗弯刚度值

由表8可知,不同预应力工况下的高钒索和不锈钢索的α值比较接近,并随着直径的增大逐渐减小,同时与直径分别满足式(13)、(14).由高钒索和不锈钢索试验所得α值与式(13)、(14)拟合的α值的对比见图3.

α=0.0006d2-0.0310d+0.6996,14≤d≤26

(13)

α=-0.0008d2+0.0206d+0.3685,14≤d≤26

(14)

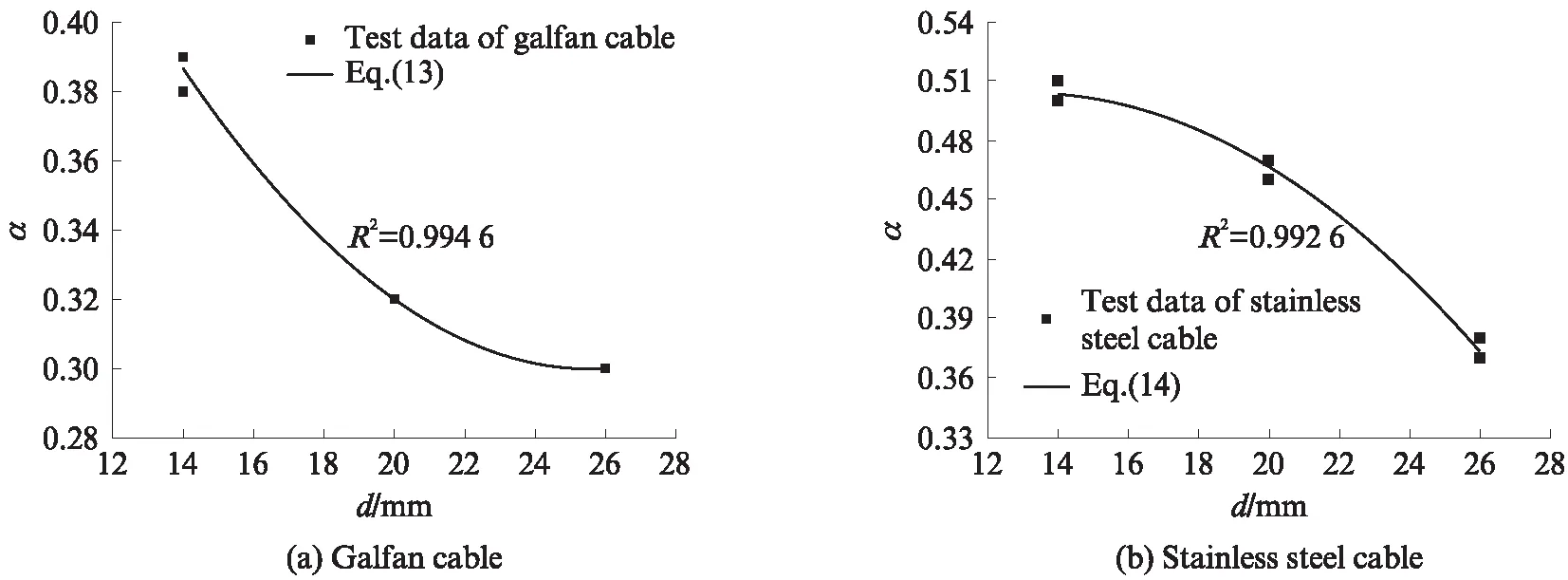
图3 拉索抗弯刚度试验值与计算值对比Fig.3 Comparison of bending stiffness of cable test value with theoretical value

3 结论

(1)提出了基于Bernoulli-Euler理论的几何抗弯刚度迭代求解方法,6种型号钢拉索在不同预应力工况下识别的几何抗弯刚度基本接近,验证了该方法的正确性.

(2)对于高钒索和不锈钢索来说,随着钢丝层数的增加,拉索直径的增大,几何抗弯刚度也逐渐增大.

(3)高钒索和不锈钢索几何抗弯刚度可取为αEImax.在相同直径下,不锈钢索α值明显大于高钒索,且随着直径的增加,2种钢拉索的α值均有降低的趋势.