学生批判性思维的培养策略

田志明

【关键词】批判性思维 重塑 小学数学

一、源起：教师的不在意VS学生的执着研究

（一）第一次震撼

在最近的毕业总复习练习时遇到这样一道题：在一个长50厘米、宽30厘米的长方形中，最多可以画多少个直径为6厘米的圆？

这可谓是一个经典的老题目，我也曾专门讲解过此类题目的解题方法（用长方形的长和宽分别去除以直径，看长和宽分别包含多少个直径，然后相乘得到总个数）。具体解答过程如下：50÷6=8（个）……2（厘米），30÷6=5（个），8×5=40（个）。

从练习反馈来看，绝大多数学生都是这样做的。面对这种解题方法和结果我也没有丝毫的质疑。

次日，我班学生赵元丞拿着他的作业本找我，说昨天那道题的结果是错误的，并“亮”出了他的实证研究图（图略），看到这个图的第一眼，我被这个学生的执着研究行为震撼了：他竟然不厌其烦地将图完整地画了出来。由于作业纸长和宽不足以画下题目中的数量，他特地按1：2缩小画出来，并且画得很精确。想一想，这41个圆不是好画的，不但大小一致，而且圆心位置也要定位准确，这对教师来说都不容易，更何况是一个学生，可以想象他为了验证自己的想法花了多大的心血。

在当天的课上，我特地让他向全班学生讲解了自己的做法，给予了表扬，并告诉学生，我们要向赵元丞学习：不拘泥于常规方法，创新思路，灵活解决问题。

（二）第二次震撼

无巧不成书。一次家庭作业的测试题中又有一个类似的题目：在长为12.4厘米，宽为7.2厘米的长方形纸中最多能剪多少个半径为1厘米的圆？

所有的反馈几乎跟上次一样：绝大多数学生的做法是：12.4÷2=6（个）……0.4（厘米），7.2÷2=3（个）……1-2（厘米），6x3=18（个）。

赵元丞同学提供的答案是21个，具体摆法如图1：

赵元丞同学提供了两种摆法。第一种摆法（如图2），即把圆看成正方形，再计算最多能剪多少个正方形，这种排列方法的特点是圆形每行每列的个数完全相同。第二种摆法（如图3），经过计算，发现从高度上看，第二种排列方式比第一种排列方式大约少了0.2679厘米（也可以从图上直接看出第二种排列方式，两层圆之间的距离小于两个直径），照这样排列下去，如果再排几层圆，那么第二种摆法所节省的空间足以再容纳一层（当层数足够多时，两种排列相差的层数还不止一层）。相比于第一种排列方式，在都符合条件的情况下，第二种排列方式要更节约空间。

虽然具体数据计算的证明涉及的相关知识远远超过了学生的现有水平，但六年级的学生还是可以从形象的排列方法中理解认可第二种排列的特殊性。

二、诊断：面对学生的执着研究，教师为何不在意

上述案例也许是一个“特殊”事件，但还是让我诚惶诚恐，并不仅仅是因为学生研究能力对教师的超越，更让我“惭愧”的是面对学生的执着研究，一开始我竟然是不在意的态度。幸好面对学生第二次执着研究时，我醒悟了，我意识到我们缺失了一种重要的素养——批判性思维，我感觉到我们不少小学数学教师的格局是否真的被局限于“小”的范围了。

（一）教师自身批判性思维素养的欠缺

批判性思维是一种高品质的思维，具有一定的深刻性，它对教师自身素养有一定的要求。如果教师没有形成批判性思维的良好素养，那就很难在潜移默化中影响自己的学生;如果教师没有对相关问题进行深入的思考，那批判性思维就会不复存在。然而，在现实教学中不少教师对教学中出现的一些反常规现象与问题，往往因不在考试的范围或者需要花费大量的精力而采取回避的态度，进而也导致了教师自身批判性思维素养的欠缺。

（二）对批判性思维价值的理解偏颇

当下，不少教师对批判性思维价值的理解存在偏颇的一面，认为是不接地气、高大上的观念。其实批判性思维倡导的是面对问题寻找新的认知方式。“批判性”并不意味着“坏”或“错”，也并不意味着“批评”或“打击”。相反，它意味着在解决问题的时候要“看到更远处”，意味着自我内在的反思，进而科学有效、正确合理地解决问题。

（三）批判性思维并未真正受到重视

在不少教师心中，批判性思维并未真正受到重视。教学目标的定位往往更关注学生是否学会，即学生是否会做题。对学习过程中的对话、质疑、批判与创意等思维习惯与能力的培育往往蜻蜓点水一掠而过。殊不知，批判性思维是学生学习的“利器”，如果一个学生拥有良好的批判性思维，我们还用担心他不会学习吗？还用担心他学不好吗？

三、矫治：重塑批判性思维

重塑批判性思维，我们需要对批判性思维进行再认识，不断提升教师自身的批判性思维，同时也要重视对学生批判性思维的培养，进而达到教学相长，促进师生内化生成良好的批判性思维。

（一）对批判性思维内涵的再认识

1.批判性思维是教育与生活的内在品性

批判性思维是西方思想的一个核心词汇和重要精神。两千多年前的苏格拉底就倡导在接触某种有价值的观念时要提出深刻的问题，而非直接接受，他的努力和推动形成了影响深远的问答法，也叫苏格拉底法、产婆术、精神助产术。批判性思维是教育与生活的内在品性。

2.批判性思维的两个维度

批判性思维具有认知技能和精神气质两个维度，认知技能包括解释、分析、评估、推断、说明和自我管制等;精神气质包括对于生命或人生的一般态度、对待特定议题或问题的态度等。我个人认为批判性思维伴随着学习的整个过程，是让学习真正发生的生发器。

（二）提升教师自身的批判性思维

1.改变传统观念，认识到批判性思维的重要性

在21世纪初的课程改革中，批判性思维已经频频出现于课标之中，但是在实际的课堂教学中，批判性思维并未真正受到重视，教师往往习惯于关注学生对知识的理解和掌握程度，而忽略所学内容的价值与意义，忽略学生內心的体验与理解。这一现象也反映出以独立判断和独立人格为基础的理性精神、健康而富有创造性的怀疑精神在当前教师中缺失，而这种理性精神和怀疑精神正是批判性思维的精髓所在。

2.向儿童学习，发展自身的批判性思维的素养

教师的批判性思维往往来自自身对问题的反省、反思、反问，而引发教师批判性思维的素材、事件、现象的源头往往来自学生：不同难度的教学内容、不同学习能力的学生、对待学习的不同态度等往往产生各种各样的教学反馈。如果教师对这些现象熟视无睹，那就与教学的“美好”擦肩而过;反之，如果教师以儿童学习的视角，常常用批判性的眼光去观照，久而久之，教师的批判性思维就会形成，自身的批判性思维的素养自然会得到提升。

（三）重视对学生批判性思维的培养

1.融入日常教学，潜移默化地培养学生批判性思维

培养学生的批判性思维，可以融入日常教学潜移默化地培养。以小学数学学科为例，在教学正比例、反比例的相关知识时，不少学生简化判断的程序和标准，简单地认为：两个量如果是相除的关系，只要比值不变，就成正比例;两个量如果是相乘的关系，只要乘积不变，就成反比例。当遇到判断“圆的直径不变时，圆的周长和圆周率成什么比例时”就会不假思索地判断为成正比例。殊不知判断正比例还有一个重要条件：两个量要符合“一个量变化，另一个量也跟着变化。”而圆周率是不会变化的，而且当圆的直径不变时，圆的周长也成为不变量。由此可以判断：当圆的直径不变时，圆的周长和圆周率不成比例。经过以上批判性思考，学生会对正比例的内涵有一个重新的、完整的、深刻的认识。

2.借助特殊素材，进行专项系统的批判性思维培训

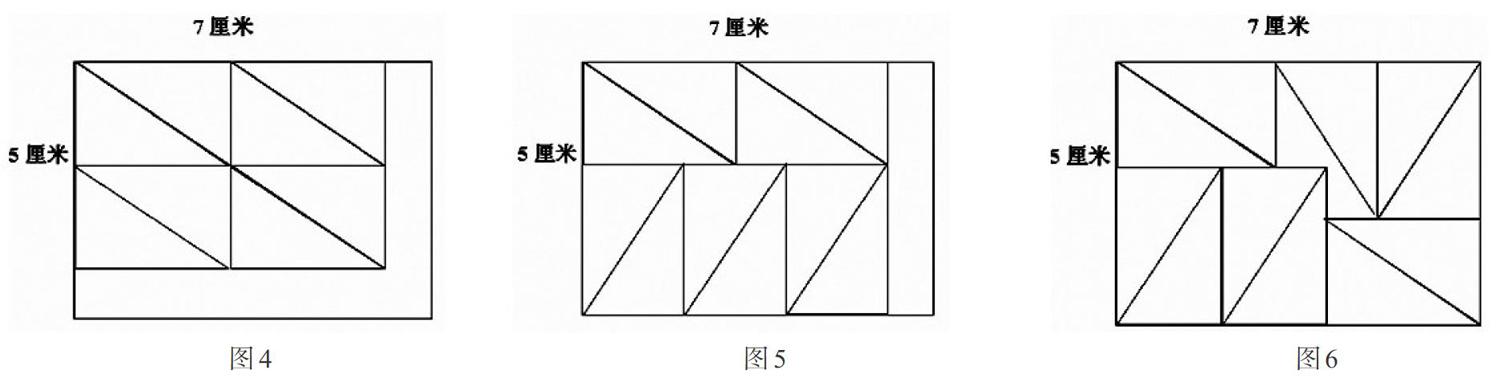
培养学生的批判性思维，可以借助特殊素材进行专项训练。本案例中的素材就是一个较好的研究素材，我们还可以研究在一个长方形里画（剪）图形（长方形、正方形、三角形等）。例如，林林要做直角三角形小旗，两条直角边分别为2厘米和3厘米。如果用长7厘米、宽5厘米的长方形纸，你认为最多能做出多少面这样的小旗？本素材可以分几个层次设计问题，引导学生探究，培养学生的批判性思维。第一个层次：对用大图形面积除以小图形面积的方法进行批判性思考，此方法不符合生活现实，建议用对应边相除的方法;第二个层次：对单一横向排列或单一纵向排列（出现剩余材料较多）的方法进行批判性思考，此方法不够灵活，应该根据实际情况横放与竖放相结合;第三个层次：对前两种“有固定路子”的方法进行批判性思考，提倡更灵活的横竖穿插结合的方法。（如下图）

学生赵元丞的执着研究让我的批判性思维意识觉醒，是他让我寻找到儿童思维力偏弱的原因之一，也是他让我明白：我们小学数学教师不能局限于“小格局”，更需要向兒童学习，并以儿童学习过程为研究对象，重塑批判性思维。