煤矿地面主通风机工况点风量风机静压准确预测研究

王海波，刘彦青，郝晋辉，赵 灿，周锦文，郑 义

(1.山西汾西矿业双柳煤矿，山西 吕梁 033000；2.煤炭科学技术研究院有限公司安全分院，北京 100013；3.煤炭资源高效开采与洁净利用国家重点实验室，北京 100013)

矿井地面主通风机工况点风量风机静压是由矿井通风系统风阻分布与地面主通风机特性共同决定的，预测地面主通风机工况点风量风机静压对于保障矿井安全高效开采具有重要作用意义[1，2]，李晓绅[3]、王洪粱[4]采用图形解析法预测分析了地面主通风机工况点风量风机静压，在前人研究的基础上，为了进一步提高地面主通风机工况点风量风机静压准确性，对由进风井至地面主通风机扩散塔之间的空气流动全过程进行了分析，针对目前地面主通风机工况点风量风机静压预测方法中未考虑风硐与风机连接处通风阻力这一问题，对主通风机风机静压风量工况点预测方程进行了修正改善，笔者以神木煤业石窑店煤矿二号风井为研究对象，采用理论分析、现场实测、数值模拟相结合的研究方法对该风井更换地面主通风机之后工况点风量风机静压进行预测研究。

1 工程概况

神木煤业石窑店煤矿一号风井与二号风井共同承担全矿井通风任务，由于一号风井承担的一采区即将回采完毕，该矿计划将一号风井关闭，全矿井通风任务均由二号风井承担。随着矿井生产能力提升，二号风井主通风机供风能力难以保障矿井日益增长的需风量要求，因此需要对二号风井主通风机进行更换，为了保障矿井通风系统安全，需要对更换风机之后的二号风井主通风机工况点风量风机静压进行准确预测，二号回风井风硐主通风机布置如图1所示。

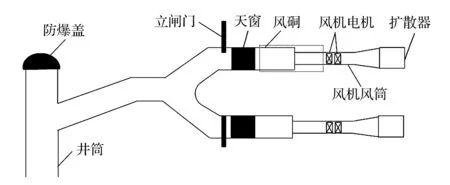
图1 石窑店煤矿二号回风井-风硐-主通风机布置示意图

2 风机静压风量工况点预测数学模型修正

现阶段矿井地面主通风机风量风机静压工况点预测过程具体步骤如下：①实测矿井地面主通风机风量-静压特性曲线[5-7]；②实测矿井通风阻力，求得矿井通风阻力特性曲线[8-10]；③以风量为横坐标，以风机静压为纵坐标，将上述实测的矿井通风阻力特性曲线与地面主风机风量-静压特性曲线置于同一坐标系下，两条曲线交点处风量、风机静压即为工况点参数。其中步骤②中实测矿井通风阻力存在问题，现阶段矿井通风阻力测试方法(MT/T 440—2008)中规定矿井通风阻力是从进风井入口至回风井风硐测压断面之间通风阻力，而工况点预测过程中需要测试矿井通风阻力是从进风井入口至主通风机风筒测压断面之间通风阻力，如果直接采用根据现阶段矿井通风阻力测试方法测得矿井通风阻力与主通风机风量-静压特性曲线进行工况点预测必然会产生误差。

主通风机风机静压风量工况点预测方法测点布置如图2所示，进风井入口至主通风机风筒测压断面之间通风阻力为进风井入口至回风井风硐测压断面之间通风阻力和风硐与风机连接处通风阻力之和，进风井入口至主通风机风筒测压断面之间通风阻力等于风机静压与矿井自然风机静压之和，见式(1)。

h3-2(Q)=h3-1(Q)+h1-2(Q)=

R3-1Q2+R1-2Q2=PF(Q)+PZ

(1)

式中，Q为回风井风量，m3/s；h3-2(Q)为风量Q条件下进风井入口至主通风机风筒测压断面之间通风阻力，Pa；h3-1(Q)为风量Q条件下进风井入口至回风井风硐测压断面之间通风阻力，Pa；h1-2(Q)为风量Q条件下风硐与风机连接处通风阻力，Pa；PZ为矿井自然风压，Pa，通过现场实测得到；PF(Q)为风机静压-风量特性曲线，Pa；R3-1为进风井入口至回风井风硐测压断面之间风阻，即矿井总风阻，Ns2/m8；R1-2风井风硐与风机风筒连接处风阻，Ns2/m8。

式(1)中，PF(Q)为以Q为自变量的函数，将PZ、R3-1、R1-2带入式(1)，求解式(1)得到工况点风量，将工况点风量带入PF(Q)计算得到工况点风机静压。

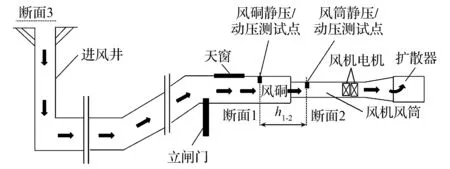
图2 主通风机风机静压风量工况点预测方法测点布置示意图

3 风机静压风量工况点预测数学模型关键参数确定

3.1 主通风机风量-静压特性曲线测定

地面主通风机风量风机静压短路测试法布置如图3所示，主通风机风量-静压特性曲线测试过程中，风机静压测试位置布置于风机叶片之前的风机风筒上，即图3中断面2位置，风机静压的本质物理意义是从风硐天窗至主通风机风筒测压位置之间通风阻力，风机静压等于断面2位置处相对静压绝对值减去动压，按式(2)计算。通过调节风硐天窗通风面积实测不同风量条件下风机静压值，采用动压法测试风机风量[11]，拟合得到以风量为自变量、以风机静压为因变量的三次多项式函数，见式(3)，不同风机运行参数条件下风机风量-静压特性曲线拟合系数及拟合度汇总数据表见表1。

PF(Q)=h4-1(Q)+h1-2(Q)=PS-2(Q)-PV-2(Q)

(2)

PF(Q)=aQ3+bQ2+cQ+d

(3)

式中，PS-2(Q)为风量Q条件下主通风机风筒断面2位置静压实测值，Pa；PV-2(Q)为主通风机风筒断面2位置动压实测值，Pa；h4-2(Q)为风量Q条件下风硐天窗入口至主通风机风筒测压断面之间通风阻力，Pa；h4-1(Q)为风量Q条件下风硐天窗入口至回风井风硐测压断面之间通风阻力，Pa；a、b、c、d分别为风机静压-风量特性曲线拟合系数。

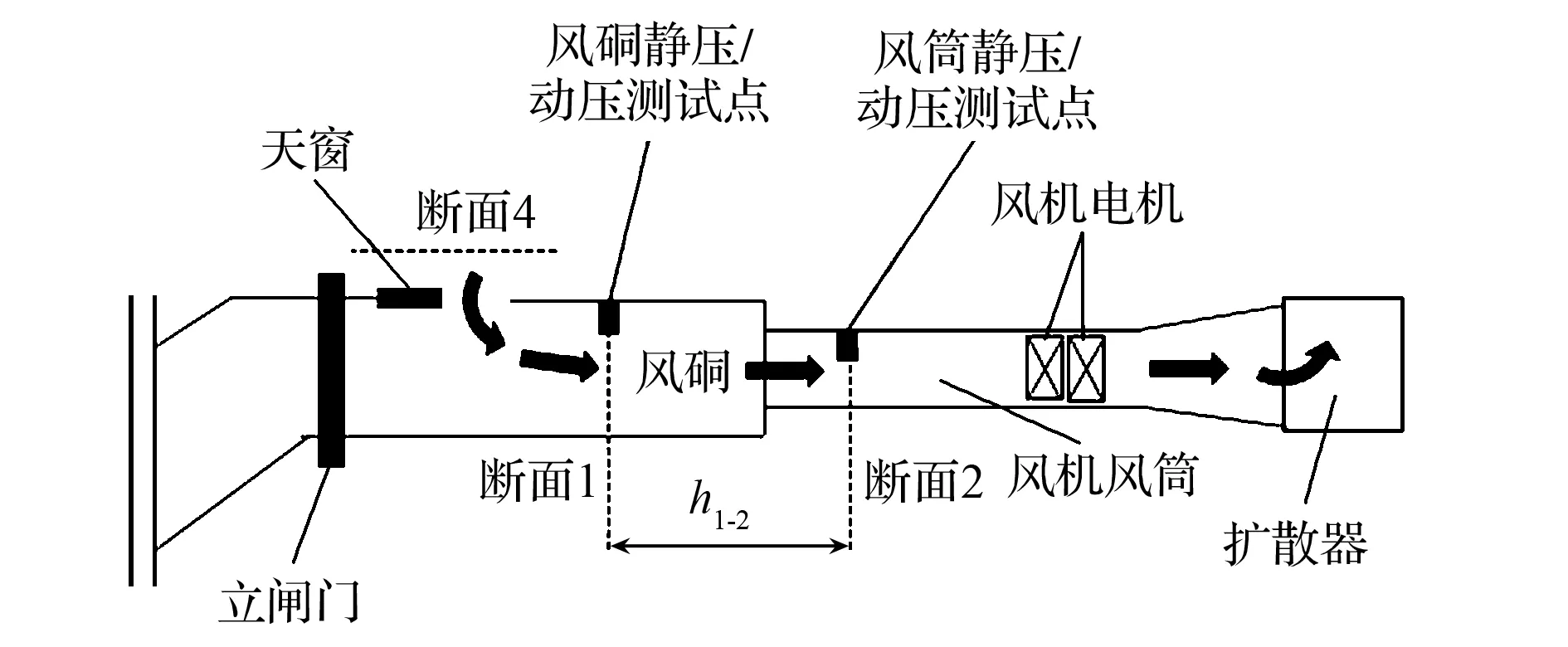
图3 地面主通风机风量风机静压短路测试法布置示意图

表1 不同风机运行参数条件下风机风量-静压特性曲线拟合系数值及拟合度

3.2 矿井总风阻测算

式(4)中矿井自然风机静压值可通过实测得到，进风井入口至回风井风硐测压断面之间通风阻力h3-1以摩擦阻力为主，风阻R3-1可近似为恒定值。根据矿井通风阻力定律，利用式(4)可直接实测计算得到矿井总风阻，矿井通风总风阻相关参数实测值汇总表见表2。

式中，PS-1(Q)为风量Q条件下回风井风硐断面1位置静压实测值，Pa；PV-1(Q)为风量Q条件下回风井风硐断面1位置动压实测值，Pa。

表2 矿井通风总风阻相关参数实测结果汇总

3.3 风硐与风机风筒连接处风阻最佳测算方法研究

风井风硐与风机连接处风阻R1-2的确定方法主要有三种：①实测图3中断面1与断面2之间全压差、风量，计算风阻；②运用流体动力学数值模拟方法求解风阻；③利用风阻理论计算公式直接求解。

3.3.1 现场实测法

如图3所示，在风硐与矿井通风系统断开条件下，通过改变风硐天窗开启面积调节风量，利用倾斜压差计实测不同风量条件下断面1与断面2之间的全压差，全压差为风硐断面1与风机风筒断面2之间通风阻力，按式(5)计算风井风硐与风机连接处通风阻力，不同风量条件下风井风硐与风机连接处通风阻力现场实测结果见表3，采用数值分析方法对风量与通风阻力之间的非线性关系进行定量拟合，拟合函数为二次抛物线形函数，如图4所示，拟合函数见式(6)，拟合度达到0.99以上，在此基础上得到风阻拟合函数见式(7)，由式(7)可知风井风硐与风机连接处风阻为非定常值且与风量大小相关，这与巷道摩擦风阻为定常值的特征明显不符，实测结果验证了风井风硐与风机连接处通风阻力为典型的局部通风阻力，局部风阻与风量大小、流通空间结构密切相关。

h1-2-C(Q)=P1-T(Q)-P2-T(Q)

(5)

式中，Q为风量，m3/s；h1-2-C(Q)为风量Q条件下风硐与风机连接处通风阻力实测值，Pa；P1-T(Q)为风量Q条件下图3中风硐断面1位置全压，Pa；P2-T(Q)为风量Q条件下图3中风机风筒断面2位置全压，Pa。

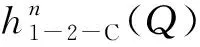
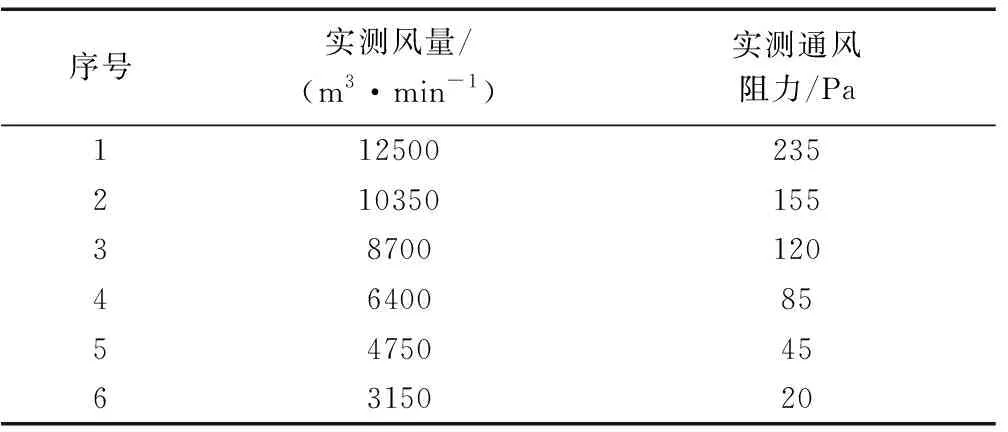
表3 风硐与风机连接处局部通风阻力现场实测结果

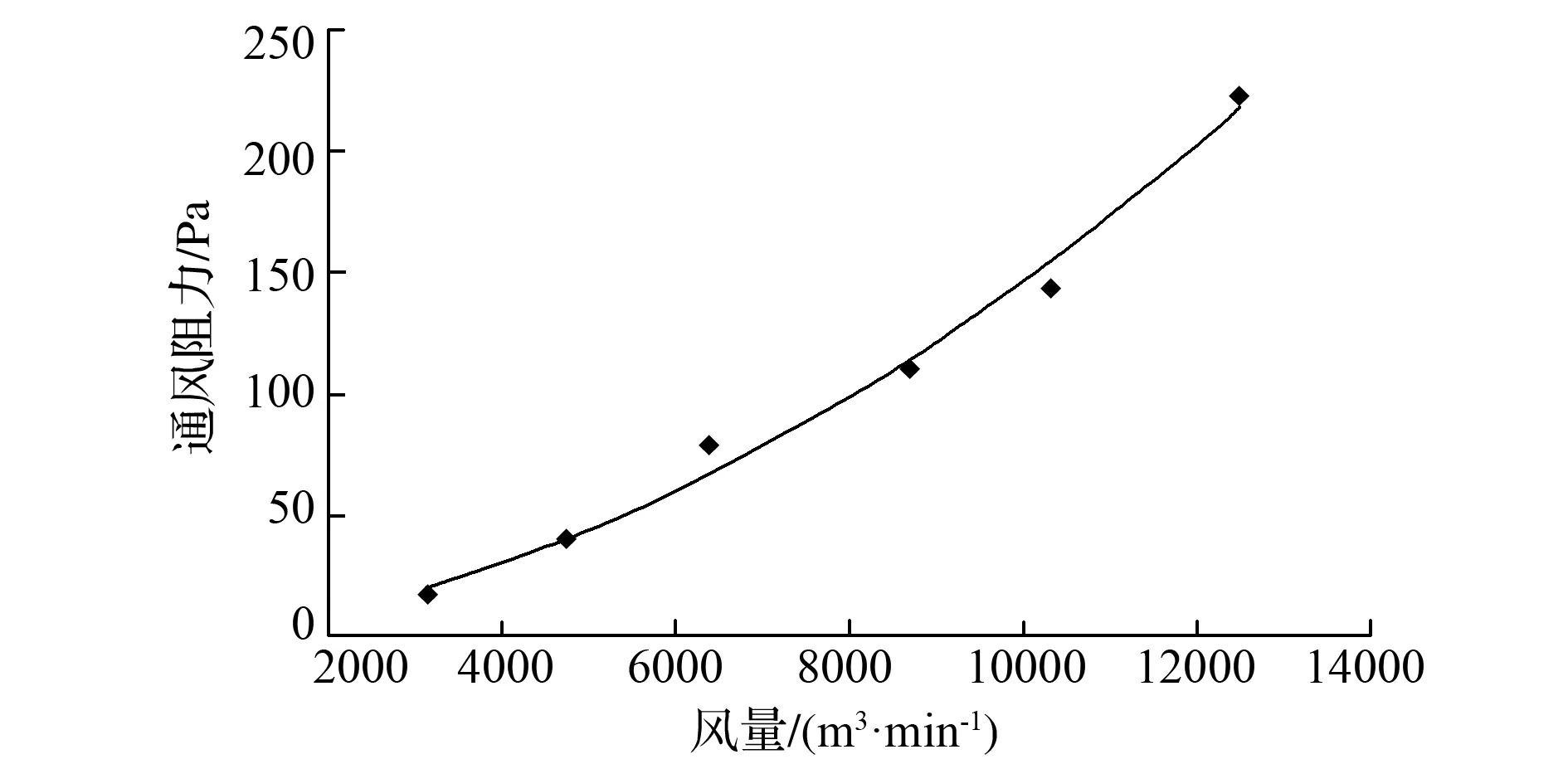
图4 回风井风硐与风机连接处局部通风阻力实测结果拟合曲线

3.3.2 数值模拟求解

采用流体动力学数值模拟方法求解风阻是建立在回风井风硐测压断面与风机风筒测压断面之间风流场结构数值模拟基础上进行的，风流场数值模拟的准确性直接影响风阻计算结果的准确性，越来越多的研究人员开始利用FLUENT数值模拟软件对矿井通风问题进行研究[12-15]。

1)几何模型。以风硐实际尺寸形状、风机风筒实际尺寸形状为基础，利用FLUENT流体动力学数值模拟软件构建风硐测压断面与风机风筒测压断面之间风流场计算模型，几何模型如图5所示。

图5 回风井风硐测压断面与风机风筒测压断面之间几何空间模型

2)数学模型。受限空间内空气流动用N-S方程组求解，满足质量、动量及能量守恒定律，式(8)为风硐与风机之间空气流动过程控制方程组。

式中，ρf为风流密度，kg/m3；u为某一位置x方向风速，m/s；v为采空区某一位置y方向风速，m/s；w为某一位置z方向风速，m/s；U为某一位置风速矢量，m/s；μ为空气动力粘度，取值为17.9×10-6Pa·s；P为气体压力，Pa；Su为x方向的动量源项，kg·m/(m3·s)；Sv为y方向的动量源项，kg·m/(m3·s)；Sw为z方向的动量源项，kg·m/(m3·s)；T为气体温度，K；k为空气传热系数，取值为0.023W/(m·K)；Cp为空气比热容，取值为717J/(kg·K)；ST为粘性耗散项，J/(m3·s)。

风硐与风筒连接处区域风流为紊流状态，描述风硐内风流场需要在N-S方程组上补充湍流模型方程组，由于风硐与风筒尺寸差异较大，风流会发生剧变，REGk-ε模型可以很好地处理高应变率及流线弯曲程度大的流动，因此湍流模型选择REGk-ε模型，式(9)与式(10)为REGk-ε模型的控制方程。

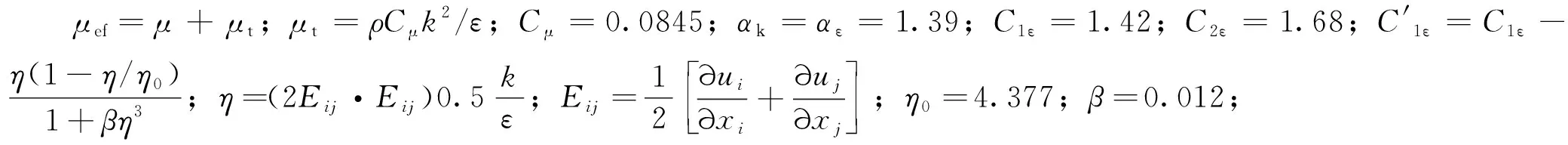
式(8)、式(9)、式(10)联立即为风硐与风机之间风流场数值计算模型的方程组，加上边界条件，就构成了风硐与风机之间风流场数值计算模型。

3)边界条件。风硐与风机之间风流场CFD计算模型的边界条件设定如下：风硐壁面、风硐顶板、风硐底板、风筒壁均为Wall(墙壁)，风硐风流入口为Velocity-in(速度入口)，风筒风流出口为Out-flow(自由出口)。

4)模拟结果。以现场实测风量值为模拟条件，模拟解算风硐测压断面与风机风筒测压断面之间风机静压场和风速场，模拟结果如图6所示。

图6 回风井风硐测压断面与风机风筒测压断面之间风速场、压力场数值模拟云图

基于风流静压场、风速场数值模拟结果，按式(11)计算回风井风硐与风机风筒连接处通风阻力，采用数值分析方法对通风阻力模拟结果与风量之间关系进行定量拟合，拟合函数为二次抛物线形函数，如图7所示，拟合函数见式(12)，拟合度达到0.99以上，在此基础上得到风阻函数见式(13)。

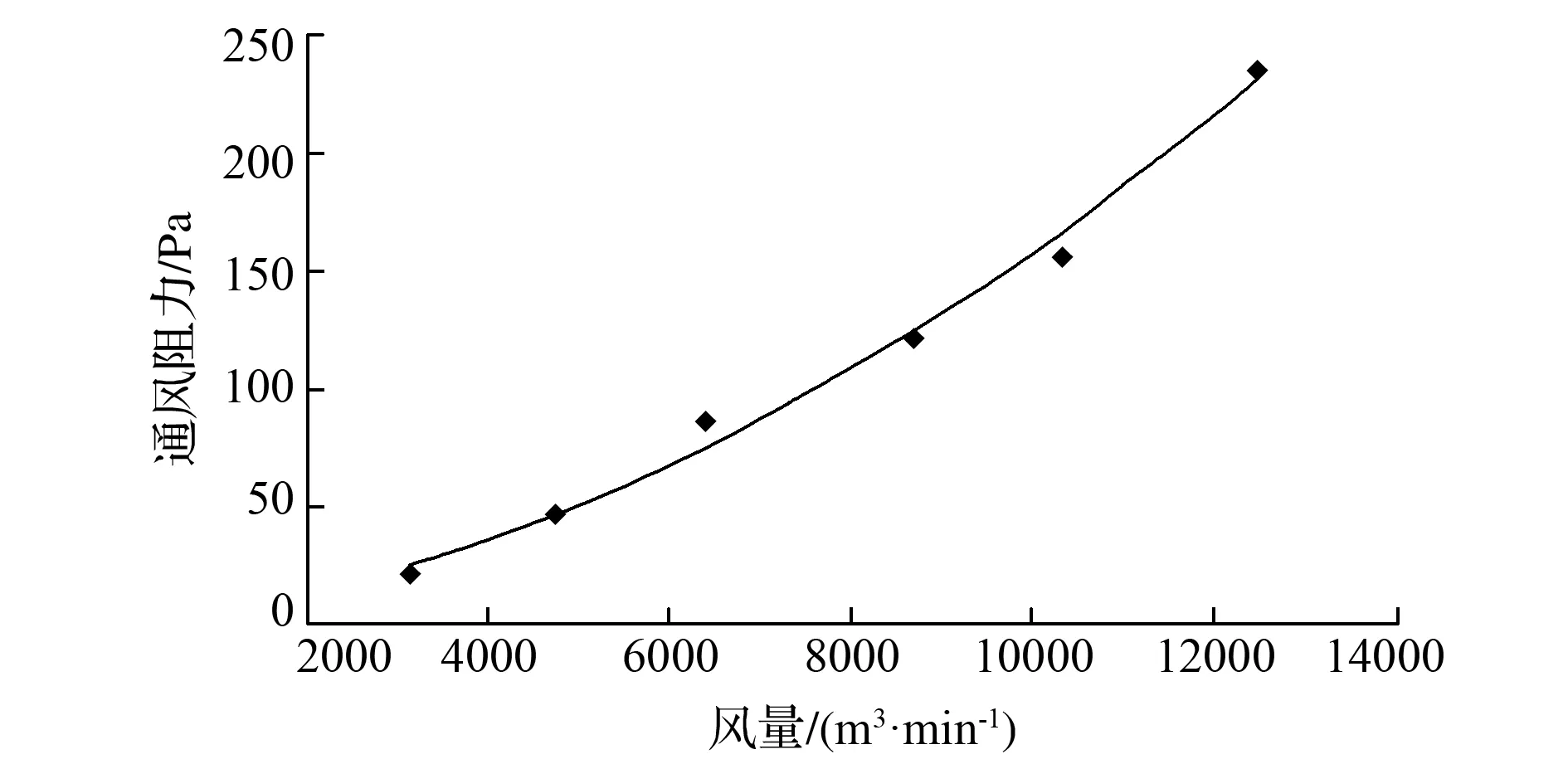
图7 回风井风硐与风机连接处通风阻力数值模拟结果拟合曲线

Pout-s(Q)-Pout-d(Q)

(11)

式中，Pin-s(Q)为风量Q条件下入口大断面平均静压，模拟结果值，Pa；Pin-d(Q)为风量Q条件下入口大断面平均动压，模拟结果值，Pa；Pout-s(Q)为风量Q条件下出口大断面平均静压，模拟结果值，Pa；Pout-d(Q)为风量Q条件下出口大断面平均动压，模拟结果值，Pa。

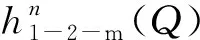
3.3.3 理论公式求解

式(14)为风硐与风机连接处通风阻力理论计算公式，式(15)为相应的风阻计算公式，风阻与风硐风机风筒尺寸相关，与风量无关。

式中，h1-2-L(Q)为风量Q条件下风硐与风机连接处通风阻力理论公式计算值，Pa；R1-2-L(Q)为为风量Q条件下风硐与风机连接处风阻理论公式计算值，Ns2/m8；ρ为风流密度，kg/m3；v2为风机风筒断面2位置风速，m/s；S2为风机风筒断面2断面积，m2；S1为风硐断面2断面积，m2。

3.3.4 对比分析

采用上述三种方法分别对神木煤业石窑店煤矿二号风井回风井风硐与风机连接处通风阻力及风阻进行了测算，其中现场实测方法测试结果准确性最高。现场实测方法存在测试过程中需要频繁调节风量可能影响矿井正常生产的缺点。数值模拟方法和理论公式计算方法具有成本低、不存在现场测试安全隐患等优点，但其通风阻力测算结果准确性有待验证。为了获得安全、高效的回风井风硐与风机连接处通风阻力测算方法，需要对数值模拟方法和理论公式计算方法测算结果准确性进行验证，式(16)、式(17)分别为通风阻力理论公式计算结果与实测结果相对误差计算公式、通风阻力数值模拟结果与实测结果相对误差计算公式，回风井风硐至风机风筒之间通风阻力数值模拟与理论计算结果误差对比情况、回风井风硐与风机连接处通风阻力数值模拟与理论公式计算结果误差对比情况如图8所示。

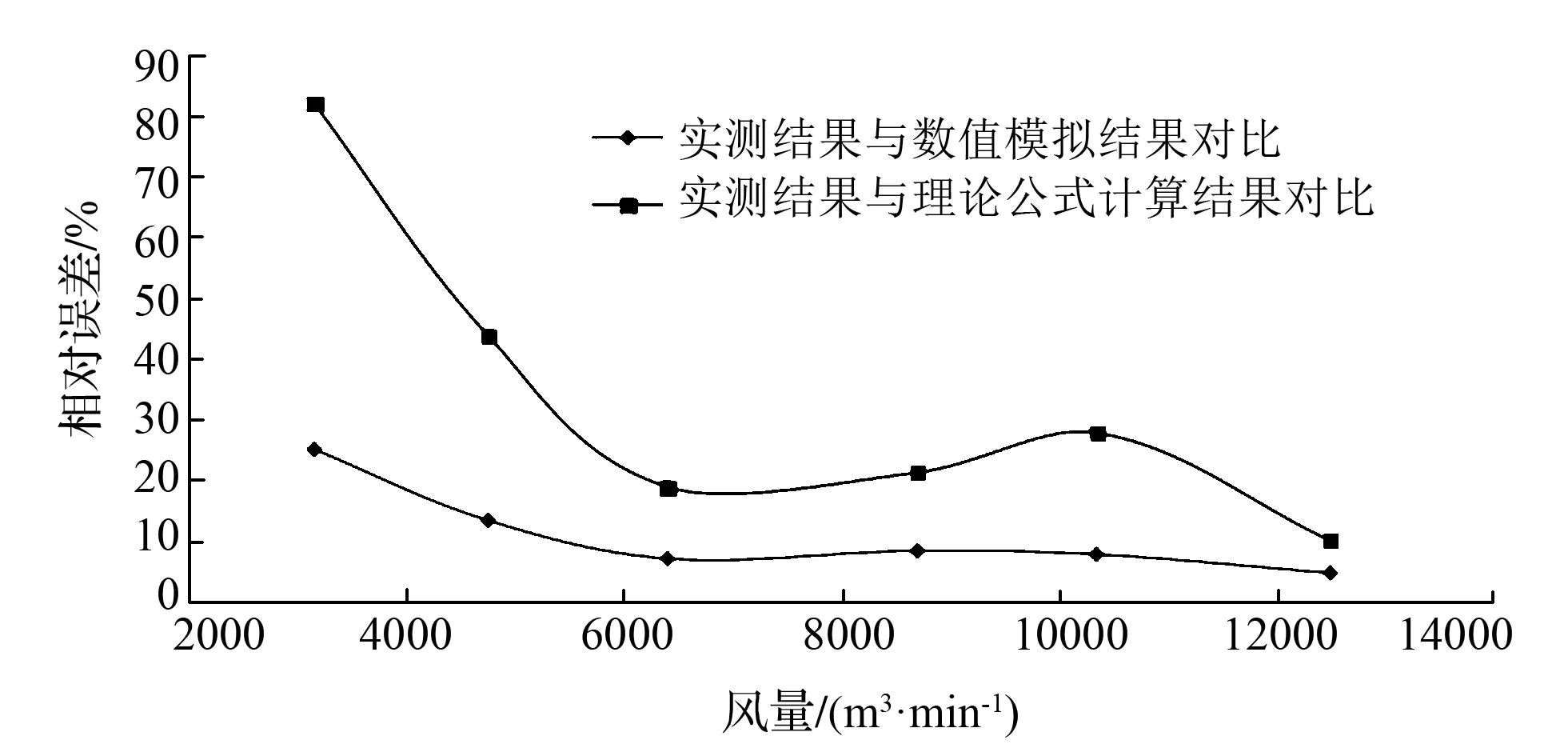
图8 风硐与风机连接处通风阻力数值模拟与理论公式计算结果误差对比

由图8可得，理论公式计算结果与现场测试结果之间相对误差最高达到80%，而数值模拟结果与现场实测结果之间相对误差基本在30%以内，且风量越大，相对误差越小，在满足工程精度的前提下，采用数值模拟方法是最佳的风硐与风机连接处通风阻力测算方法。

式中，dL为通风阻力理论公式计算结果与实测结果相对误差，%；dS为通风阻力数值模拟结果与实测结果相对误差，%。

4 矿井地面主通风机工况点预测结果分析

式(18)为未考虑风硐与风机连接处通风阻力的风机工况点风量求解方程，将矿井自然风压、风机风量-风机静压特性曲线、矿井总风阻带入式(18)求解工况点风量，计算结果见表4。式(19)为采用数值模拟求解风硐与风机连接处通风阻力情况下的风机工况点风量求解方程，将矿井自然风压、地面主通风机风量-风机静压特性曲线、矿井总风阻、风硐与风机连接处风阻带入式(19)求解工况点风量，计算结果见表4。式(20)为采用现场实测求解风硐与风机连接处通风阻力情况下的风机工况点风量求解方程，将矿井自然风压、地面主通风机风量-风机静压特性曲线、矿井总风阻、风硐与风机连接处风阻带入式(20)求解工况点风量，计算结果见表4。根据地面主通风机风量计算结果，利用式(3)计算工况点风机静压，计算结果见表4。地面主通风机风量测试方面，动压法比静压差法测试准确性更高[5]，采用动压法实测风机投入运行之后风量，实测结果见表4。

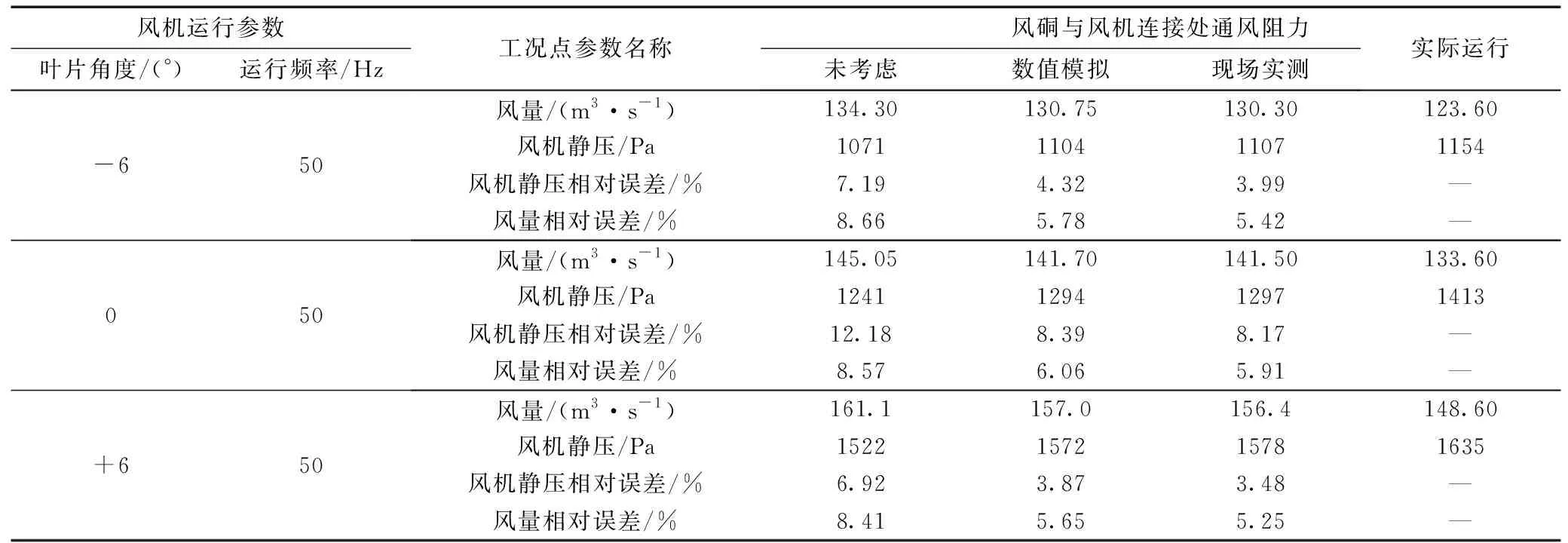
表4 地面主通风机工况点风机静压、风量预测结果及误差对比情况

未考虑风硐与风机连接处通风阻力的预测方程计算结果与实际工况点之间风量和风机静压之间最大相对误差达到8.66%、12.18%，考虑风硐与风机连接处局部通风阻力的预测方程计算结果与实际工况点之间风量和风机静压最大相对误差分别为6.06%、8.39%。未考虑风硐与风机连接处通风阻力的预测方程计算结果与实际工况点之间风量和风机静压之间相对误差明显大于考虑风硐与风机连接处通风阻力的预测方程计算结果与实际工况点之间风量和风机静压相对误差，研究表明风硐与风机之间局部通风阻力对于地面主通风机工况点具有不可忽略的影响作用，考虑风硐与风机连接处通风阻力的主通风机风机静压风量工况点预测方法能够显著提高风机工况点风量、风机静压预测的准确性。

aQ3+bQ2+cQ=R3-1Q2-PZ

(18)

5 结 论

1)揭示分析得到目前工况点预测方法中存在未考虑风硐与风机之间局部阻力的问题，以神木煤业石窑店煤矿二号风井更换地面主通风机之后工况点风量风机静压预测为研究，采用现场实测、数值模拟和理论公式三种方法分别计算风硐与风机连接处通风阻力，研究表明采用数值模拟方法能够准确计算风硐与风机之间通风阻力，在此基础上建立了非线性形式的风硐与风机连接处风阻计算公式。

2)结合实测的风机风量风机静压特性曲线、矿井通风阻力特性曲线，建立了考虑风硐与风机之间局部阻力影响的主通风机风机静压风量工况点预测方程，研究表明风硐与风机连接处通风阻力对于地面主通风机工况点具有不可忽略的影响作用，考虑风硐与风机连接处通风阻力影响的主通风机风机静压风量工况点预测方法能够显著提高风机工况点风量、风机静压预测的准确性。