再探《数学通报》2268题

刘 鹏 杨光伟

(浙江师范大学教师教育学院 321004)

1 问题呈现

《数学通报》2015年10月号问题2268:

试证明:等式1

(1)

对于该问题,供题者柳冉在《数学通报》2015年第11期“2015年10月号问题解答”[1]中反复利用正弦、余弦的积化和差等公式及一定的运算技巧给出了证明.

其次,黄盛清老师在《数学通报》2017年第6期《基于余弦7倍角公式求几个一元三次方程的解及其应用》[2]一文中通过余弦多倍角公式和方程的关系给出了证明.

笔者认为,此命题结论结构优美,在阅读过程中思考能否简化其证明的同时,也有其它发现.

2 尝试简证

文献[2]有结论如下:

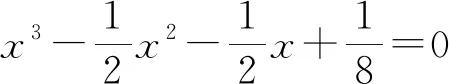
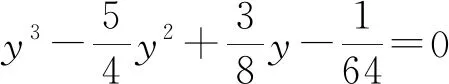
以上两结论是从余弦7倍角出发,给出了一个一元七次方程的解,分解一元七次方程进而得到几个一元三次方程的解.最终根据一元三次方程3个根与系数的关系证明式(1).笔者在探索过程中,发现由结论1推出结论2的证明过程可以简化许多,本文给出结论2的证明如下.

证明将结论1的方程

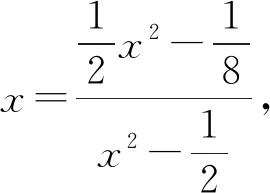
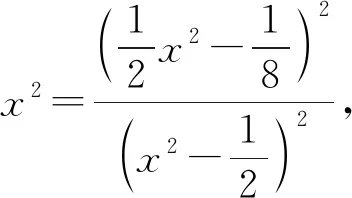
(2)

(3)

根据代换x2=y可知式(3)的解为

由此,结论2证毕.

进而证明式(1),根据式(3),令y=1-u,得

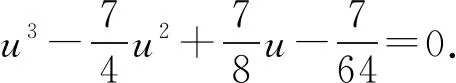
根据一元三次方程3个根与系数的关系,得

得等式1

可见,根据x巧妙的自身代换,将黄盛清老师的部分证明过程简化许多.并且,在探究过程中,也有新的发现.

3 探究发现

在思考过程中发现,将式(2)先变形为

再变形为

(4)

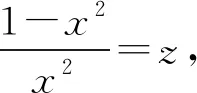
又因为式(3)的证明过程中令x2=y,故

将式(3)直接变形为

z3-21z2+35z-7=0,

(5)

由结论2知式(5)的解为

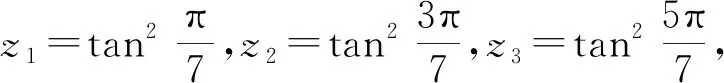
由此,得到结论3.

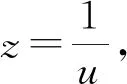
-7u3+35u2-21u+1=0.

(6)

由式(5)知式(6)的解为

由此,得到结论4.

受等式1的启发,由结论2根据一元三次方程3个根与系数的关系,得

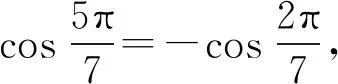
(7)

同理,由结论3可得

(8)

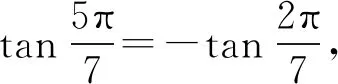
(9)

同理,由结论4可得

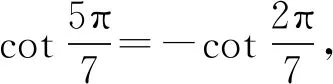
(10)

4 应用

显然,根据一元三次方程的自身代换,不仅可以使得证明过程更加简洁,还可以得到一些漂亮的结论.例如,通过结论2、结论3和结论4,得到了等式2、等式3、等式4三个结构优美的等式;同时,还可得结论5与结论6.最后，进行简单的应用.

证明由式(10)化简可以直接证明.

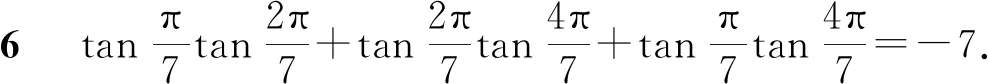
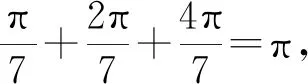
两边平方

(11)

根据式(8)等式左边为

等式右边展开为

根据式(8)可得

故

证毕.

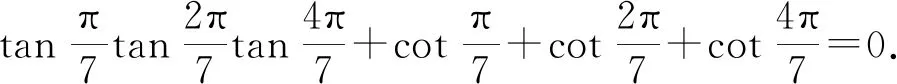
证明由式(8)得

又

故

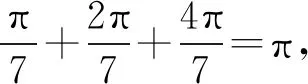
又

则

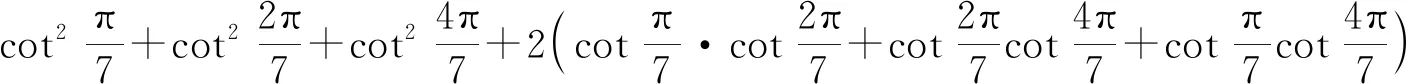
=7,

利用二倍角的转化和函数的最值判断,可得

故

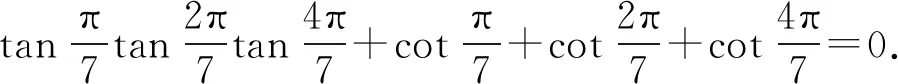
美国数学家哈尔莫斯说过,问题是数学的心脏[3].面对同一个数学问题,总有其值得我们思考之处;在探索发现的过程中,总会有意想不到的收获.本文通过对余弦7倍角公式应用方面的探究,简化了证明,并得到了一些漂亮的结论.期望能够引起更多数学爱好者的共鸣.