回归教材：提升学生核心素养的有效途径

唐 永

(江苏省江阴市第一中学 214400)

教材是学生在校学习的主要资源，是教师进行课堂教学的重要依据，是教学的工具和抓手.历年高考中有大量试题直接源于教材或由教材中的例、习题改变而来.因此，回归教材是高考复习中一个非常重要的环节.什么是回归教材呢？回归教材是指带着一定的目的、任务或问题回到教材中重新审视教材的过程.回归教材不是简单阅读教材、不是简单罗列知识、不是简单梳理方法、不是对教学过程的简单重现，而是对学科知识脉络的建构、对教材编者意图的领悟、对教材隐性知识的挖掘、对学科知识本质的把握.

1 “回归教材”的现状

在高考复习过程中，大多以一本教辅资料或自编的导学案为主，基本框架包括：考纲要求、知识梳理、课前练习、典型例题、课堂反馈、课后作业.预习过程中遇到知识梳理这块内容，多数学生选择“参考书”或者等老师讲，而不是主动看教材.

做作业时对于遗忘的公式、定理等，学生往往会翻看各种“宝典”，或求助邻位的同学.

学生的课桌上摆放的是各种各样的复习资料，几乎看不到数学课本，学生表示“课本没什么用啊”、“书早带回家了”，更有甚者表示“高一、高二课本早就扔了”.

不少教师表示，在复习阶段，课本也是常备常翻的，特别遇到一些有争论的地方，但利用宝贵的课堂时间梳理课本，恐怕费时费力，担心影响复习效率.

不少教师也深刻知道：“回归教材”的重要性，教材是高考命题的“源泉”，每年高考试题中有大量题都能在课本中找到“影踪”，但那都是“事后诸葛亮”，表示很困惑和无奈.

从时间上来看，多数教师会安排在高三三轮复习或高考考前，集中一段时间让学生翻看课本，看书中的概念、公式和定理等，或者选出一些课本题目让学生做.

2 “回归教材”的策略

我国著名的教育家叶圣陶先生曾说：“教材无非是个例子，它只能作为教课的依据，要教得好，使学生受益，还要靠教师善于运用.”在处处讲求效率的高三复习阶段，如何结合课程标准、考试说明再次研读教材、运用教材，提升教学效率，尤其是提高学生的学习效率是重中之重.那么，如何回归教材呢？经过多年的实践与反思，笔者有一下思考和体会.

2.1 研读核心概念，提高抽象思维能力

由于受应试教育的影响，起始年级的教学中经常出现忽视概念的教学，最常见的是照本宣科，把形成概念的生动过程变为简单的“条文加例题”；或者虽有揭示概念的过程，但简单浅薄，内容贫乏，一带而过.这样势必造成数学概念与解题脱节的现象， 许多对概念掌握不准确或不够灵活的学生在解题中出现错误以后，往往找不到问题的根源.在一轮复习中，对一些核心概念要舍得花时间，带领学生重新研读教材，领悟其本质特征.如，通过再次学习“函数单调性概念”，帮助学生做到从以下几个方面深刻理解：

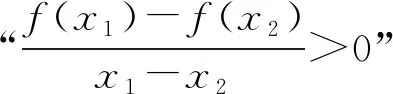
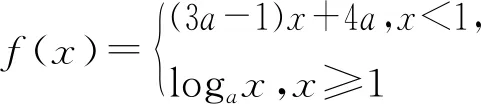
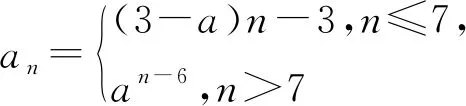
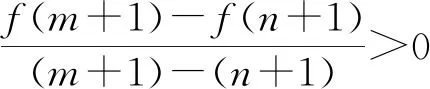
2.2 重温公式推导，提升认知高度

对于数学概念、公式、法则、定理等，高三学生的一个通病是知其然，而不知其所以然.例如，“等比数列的前n项和公式”是高考反复考的知识点，要求学生熟练掌握、灵活运用.然而，大多数教师复习本节内容时，对公式的推导过程一滑而过，仅是强调记住公式，然后就是大量的例习题，反复地应用公式，以达到灵活运用的目的.对这个知识点的复习，仅仅停留在熟记公式、运用公式解题的层面上是远远不够的，学生对公式的认识是不完整、不深刻的，他们不清楚知识的来龙去脉，不能完整地构建知识网络，不能体会到公式推导过程中所蕴含的分类讨论、函数与方程、转化与划归、减元等思想方法，这也正是本节课要揭示的.因此，在一轮复习课上，教师宜设置一些递进的问题串，重温公式推导过程，揭示其思想方法.以“等比数列的前n项和公式”为例，设置如下问题串：

问题1你还记得等比数列的前n项和公式吗？

主要是强调对q=1和q≠1需分两种情况讨论.

问题2教材是如何推导公式的？其隐含什么思想方法？

采用错位相减法：两边同乘以q，错位相减得Sn-qSn=….

主要是“减元”的思想，实现无限到有限的转化.

问题3除了两边同乘以q外，还可以乘以什么？

问题4还有别的方法推导公式吗？

法1:Sn=a1+a1q+…+a1qn-1

=a1+q(a1+…+a1qn-2)=a1+qSn-1,

又Sn=an+Sn-1，所以Sn-qSn=a1-qan，

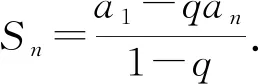
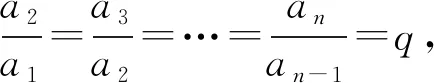
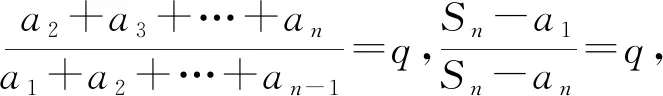
化简得Sn-qSn=a1-qan，

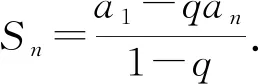
问题5与等差数列的前n项和公式推导方法——倒序相加法相比较，有什么共同之处？

本质上是一致的，都是以消相为目的，实现无限到有限的转化.

2.3 再现教材例题，发掘隐含功能

一轮复习教辅资料以题目的归类为主，所以在复习时教材例题的呈现和挖掘就显得可有可无，当然这也源于教师对教材题目功能挖掘的不够.但研究教材的例题不难发现，从格式的规范性，到解题的模式化，到数学思想方法的呈现，以及新知的不同程度的理解，教材中的例题无不体现其权威性.在复习过程中，应切实体现以教材为本的原则，整合多方面的力量，真正吃透教材上例题的示范功能，辅以变式、拓展，揭示它们的深刻内涵，只有这样，这些例题的示范性和训练价值才能真正得到展示，并引领学生达到新的高度.

案例3在复习“两角和与差的三角函数”这一节，用PPT投影教材中两道例题：

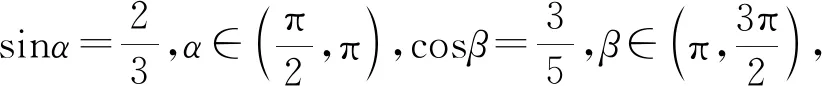
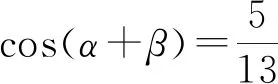
sinα=sin[(α+β)-β]

=sin(α+β)cosβ-cos(α+β)sinβ

即可.它们的本质都是利用“角变换”思想进行“未知角”和“已知角”的等价转化.类似的给值求值问题在课本中还有很多，在高考题中也是高频率出现的，只要学生真正把握这类问题解法的本质，基本上就可以解决这类问题了.

2.4 梳理教材，寻找解题方法

高考题虽然不直接来源于课本一模一样的例、习题，但对重要的数学思想和数学方法的考查无一例外地来自于教材.因此，真正理解和运用好教材所蕴含的数学思想方法，总会为陌生的高考试题寻找到最快速的解题方向.例如，“取对数”、“取倒数”、“分子或分母有理化”、“算两次”等方法，其中“算两次”在苏教版教材中多次出现：等差数列前n项和公式的推导过程中使用的倒序相加法，两角和与差的余弦公式的推导方法，立体几何中“等体积法”求点到平面的距离等.在高考中，“算两次”常常被作为重要的数学方法加以考查.2010年江苏卷第19题是一道数列与不等式的综合问题，需要运用算两次方法求解.2016年江苏卷附加题第23题，再次对算两次方法进行了考查.

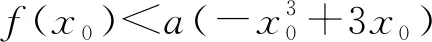
解(1)(2)略.

案例4中取对数看似神来之笔，配置苏教版必修1第61页例6(试用常用对数表示log35)，例6的解答就是采用两边取常用对数的方法，进一步地得到对数换底公式.

案例5(2018年江苏卷第13题)在△ABC中，角A，B，C所对的边分别为a,b,c,∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1,则4a+c的最小值为______.

解因为S△ABC=S△ABD+S△CBD，

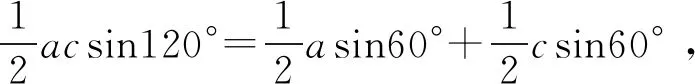
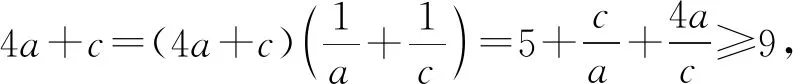
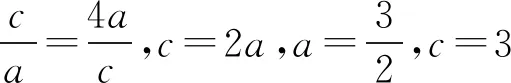
本题采用了“等面积法”，对三角形ABC的面积算两次，是诸多方法中最为简洁的方法.

2.5 开发教材，应用“二手”结论

高考命题“即源于教材，又高于教材”.因此，高三复习需要对教材重新开发，结合高考命题实际，对教材中的某些内容进行补充、拓展、改进、增补、变式、整合等.教材中结论主要以公式、定理、法则的形式直接呈现.事实上，教材中还隐含了一些结论(不妨称“二手”结论)需要开发. “二手”结论往往是高考命题的重要素材、是解答高考试题的重要工具.常见的“二手”结论如下：

结论1ex≥x+1,lnx≤x-1．

结论2与椭圆的“直径”相关的结论：

结论3斜△ABC中，tanA+tanB+tanC=tanAtanBtanC．

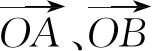
结论5极化恒等式：

案例6(苏教版必修4第83页,习题2.4第5题)求证：

|a+b|2+|a-b|2=2(|a|2+|b|2).

如何构造一个图形解释这个公式的几何意义？

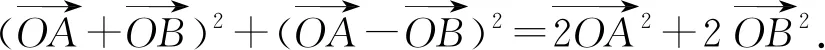
——平行四边形的性质

联想2：在平行四边形ABCD中，

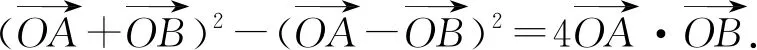
——极化恒等式

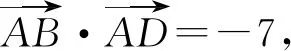
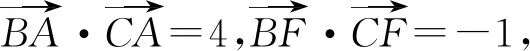
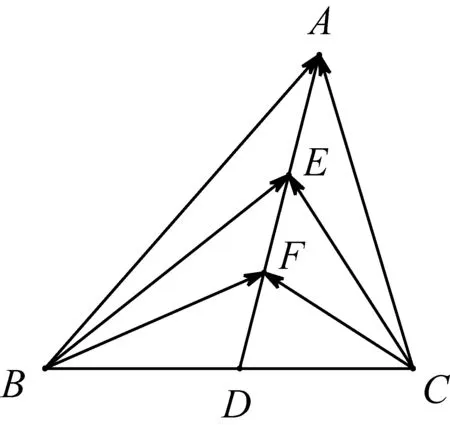
总之，回归教材是高三复习的正道.在高三复习过程中，要用教材、用好教材，从教材中追本溯源，让教材成为“源头活水”，建构章节的知识网络，挖掘知识的本源，渗透数学的思想和方法，提升教学和学生复习的效率.