新教材中周期函数内容的比较研究
李世杰 李 盛
(1.浙江省衢州市教育局教研室 324000;2.浙江省衢州第一中学 324000)
周期函数是高中数学的一块重要内容,也是高中数学教学的一个难点.2019版普通高中数学教科书中,人教A版[1]、北师大版[2]和湘教版[3]继承沿用了上一版教材中周期函数的两种定义方式,我们也曾在文献[3-8]中对这两种定义下的周期函数作过一些探讨.
长期以来,这两种定义下的周期函数处于混用状态,但由于周期函数这两种定义的内涵并不完全相同,因此产生了不少似是而非,似非而是的数学问题.下面我们对这两种定义下的周期函数进行对比研究,从函数的定义,定义域,值域,周期,最小正周期,图象特征等方面寻找联系与区别,提炼共性特征,挖掘个性特点,在比较中澄清事实真相,纠正错误认识,希望对新教材中周期函数内容的教学有所帮助.
1 周期函数定义的比较研究
1.1 两个课本定义
现行高中教科书中常用的两个周期函数定义是:
课本定义1(人教A版[1]、北师大版[2]) 设函数f(x)的定义域为D,如果存在一个非零常数T,使得每一个x∈D都有x+T∈D,且f(x+T)=f(x),那么函数f(x)就叫做周期函数(periodic function).非零常数T叫做这个函数的周期(period).
课本定义2(湘教版[3]定义)对于函数y=f(x),如果存在非零常数T,使得当x取定义域内每一个值时,x±T都有定义,并且f(x±T)=f(x),则这个函数y=f(x)称为周期函数(periodic function).T叫做这个函数的一个周期(period).
1.2 课本定义1的优点与问题
周期函数课本定义1的优点:表述简洁,形式简单,易于高中学生学习理解,掌握周期函数最本质的东西:周期函数具备周而复始的性质,所以只要研究一个周期的情况,就能推知全部了,这也是学习周期函数的初衷.与《数学手册》[9],《中学百科全书数学卷》[10]中定义完全一致.与原人教版必修4中的定义相比,明确了周期函数对于定义域的要求,即增加了一句“对每一个x∈D,都有x+T∈D”.这样修改,将原来隐含的定义域问题显性化,教学中更好操作,与物理中实际问题衔接也会更好.
但问题蕴含在定义之中.课本定义1比较简洁,约束强度不够,扩大了周期函数的外延,先看一个实例:
例1函数f(x)=1,x∈D,D={0}∪{2,3}∪[4,+∞),其周期T∈{2,3}∪[4,+∞).
解容易验证:对每一个x∈D,都有f(x+2)=f(x),f(x+3)=f(x),f(x+T)=f(x),常数T≥4.在课本定义1下,进一步可以证明,函数f(x)的周期T∈{2,3}∪[4,+∞).
注函数f(x)的最小正周期为2.在第一个周期区间[0,2)∩D={0}上,函数y=f(x)的图象只有一个点;在下一个周期区间[2,4)∩D={2,3}上,它的图象有二个点;下一个周期区间[4,6)∩D=[4,6)上,它的图象为“一条线段(少了右端点)”.这三个周期区间内的函数图象都不一致,这样的函数显然不具备周期函数“周而复始”的性质,但在课本定义1下,函数y=f(x)是周期函数,而从图象上看,却又不具有周期性.
因此,课本定义1是一个广义的周期函数定义,适合此定义的并不都是传统意义上具有“周而复始”良好性态的周期函数.
考虑到中学生的接受能力,课本定义1尽管不完美,但简洁明快,学生容易接受,有利于学生的“学”,作为课本定义是可行的,我们一直是赞同的[4].这是现行教科书中采用的约束条件最小的定义,仍不失为一个比较好的解决方案,但由于它的“简单性”,需要解决其“先天不足”随时可能导致人们出现的错误判断.
教学对策:高度重视严谨性问题.在进行高中周期函数内容的教学时,应以教科书中定义为基础,非经严格论证,绝对不能想当然地搬用其它定义下的周期函数的性质.同时,要注意排除对其扩大了的外延的讨论,即避免出现有缺陷的“周期函数”,守住例习题选用的边界(只讨论完美的周期函数如三角函数型).否则对高中学生来说,教学要求就太高了.
教学中的常见问题:将课本定义1中的“非零常数T”理解为“T同时可正可负”,误认为课本定义1与课本定义2等价,论证过程如下:
根据课本定义1,由于f(x+T)=f(x),所以f(x)=f[(x+(-T)+T]=f(x-T+T)=f(x-T),因此课本定义1与课本定义2是一致的.
事实上,f(x-T+T)=f(x-T)成立的前提条件是x-T在函数f(x)的定义域内,才能由f(x+T)=f(x)推出f(x-T)=f(x).但课本定义1下的周期函数,对任意的x∈D,并不能保证x-T∈D.如例1中函数f(x)以2为周期,3∈D,但3-2=1∉D.
这是常见教学参考资料上出现的一些周期函数结论,存在似是而非科学性问题的由来.
1.3 课本定义2的优点与问题
课本定义2的优点:表述严谨,不违背科学性,与部分大学教材中的定义一致,能避免出现似是而非的周期性问题.刚开始学时,这个定义可能比较复杂,但深入学习,对周期函数的研究反而会更简单一些.
课本定义2的问题是:形式上比较复杂,约束强度过大,缩小了周期函数的内涵.
按课本定义2,函数y=sinx,x∈R是周期函数,但它的“局部”函数:物理中的简谐运动以时间为变量的函数y=sint,t∈[0,+∞)就不是周期函数,被排除在外了,但它们具有相同的周期性,这样学生在高中物理学习中可能会造成混乱,因为物理中很多与时间相关的周期性问题都是从0开始定义的.
教学对策:
(1)从周期性质应用的角度,恰当处理“周期函数”与“函数具有周期性”问题.
如:通过教学让学生先从整体上掌握函数y=cosx,x∈R的周期性,再来理解y=cosx,x∈R+和y=cosx,x∈[0,10π ]的周期性质一点都不困难,因为从图象上看,后面二个函数的图象只是前一个函数图象的一部分.
(2)简化定义
课本定义2形式上比较复杂,约束条件较多,实际上这个定义还可简化:
由于对每一个x∈D,函数f(x)在x±T都有定义,即有x-T∈D,我们用x-T替换f(x+T)=f(x)中的x,可得f(x-T)=f(x).因此,在课本定义2的条件下,f(x±T)=f(x)与f(x+T)=f(x)是等价的.课本定义2可改进为如下的等价形式.
定义3对于函数y=f(x),如果存在非零常数T,使得当x取定义域内每一个值时,x±T都有定义,并且f(x+T)=f(x),则这个函数y=f(x)称为周期函数,T叫做这个函数的一个周期.
定义3与课本定义1形式上比较接近,“对于任意的x∈D,都有f(x+T)=f(x)”是相同的,两个定义的关键差异在于对定义域的要求不同:对于任意的x∈D,课本定义1要求“x+T∈D”,定义3要求“x±T∈D”.
注由于课本定义2下的周期函数一定同时具有正、负周期,所以直接设定T为正数也是可行的.这是因为:无论T是正数还是负数,±T均可正可负,因此课本定义2和定义3中“非零常数T”可以更明确改进为“正常数T”.
2 周期函数性态的比较研究
不同定义下的周期函数,其性态差异是非常大的,下面我们分块加以讨论.
2.1 两种周期函数的共性
课本定义1和课本定义2下周期函数的公共特性有:
①周期函数y=f(x)将无限多次地取值域中的任何值.
课本定义1下的周期函数f(x)满足f(x+T)=f(x),函数值一定无限多次单向重现.
课本定义2下的周期函数f(x)满足f(x±T)=f(x),函数值一定无限多次双向重现.
②周期函数y=f(x)的定义域D一定是一个无限集.
证明:在课本定义1下,对任意的x∈D,都有x+T∈D,用x+T替换x,得(x+T)+T∈D,即x+2T∈D,…,x+kT∈D,k∈N*,…,所以定义域D是一个无限集.
在课本定义2下,对任意的x∈D,都有x±T∈D,类似地,可推知x±kT∈D,k∈N*,…,所以定义域D也是一个无限集.
利用定义域的上述特征,某些非周期函数的判定是“一望而知”的.
例2判断下列函数的周期性:
(1)f(x)=cos 2x,x∈[0,2020];
(3)h(x)=lgx+log2(10-x).
解容易看出,函数f(x),g(x),h(x)的定义域分别为[0,2020],[2,3],(0,10),均为有限集,所以它们都是非周期函数.
③当y=f(x)是周期函数时,则它的定义域也具备相应的“周期性”.
当y=f(x)是课本定义1下的周期函数时,存在一个实数T≠0,对任意x∈D,都有x+T∈D.因此,定义域D以T为周期.
当y=f(x)是课本定义2下的周期函数时,存在一个实数T≠0,对任意x∈D,都有x±T∈D.因此,定义域D同时以T,-T为周期.
因此,当定义域D不具备以上的“周期性”时,可以断定y=f(x)为非周期函数.这提供了判断非周期函数的又一种方法.
进一步地,可以证明[4]:当DR时,CRD也具备相应的“周期性”.
还可得出结论:仅在有限个点无定义的函数必为非周期函数.
④凡是周期函数,都有无穷多个周期.
在课本定义1下,若周期函数f(x)的定义域为D,则存在一个非零常数T,使得每一个x∈D都有x+T∈D,可得x+kT∈D,k∈N*,…,在f(x+T)=f(x)中用x+(k-1)T替换x,得f(x+kT)=f(x),k∈N*,可见kT(k∈N*)均为函数f(x)的周期.
在课本定义2下的周期函数,类似可证.
所以,两种定义下的周期函数,都有无穷多个周期.
注课本定义1中最后一句“非零常数T叫做这个函数的周期”,在周期前面加上“一个”,表述会更准确.而“周期函数的周期往往不是唯一的”和“周期函数的周期可以不只一个”的说法,则是不确切的,因为这样的说法会使人误以为“周期函数的周期,在一般情况下,是不唯一的;而在特殊情况下可以是唯一的”.
⑤周期函数一定有周期,但不一定存在最小正周期
两个课本定义下的周期函数的所有周期中,并不一定存在着一个最小的正数,所以周期函数不一定存在最小正周期.如:常数函数f(x)=1,x∈R, 任意非零常数都是它的周期,但在正数集中不存在最小的正数,所以它没有最小正周期.
2.2 两种周期函数的区别
2.2.1定义域的比较研究
一个函数的周期性,不仅与函数的对应关系有关,定义域也起着关键的作用.对应关系相同但定义域不同的两个函数,它们的周期性会有很大的差异.
区别1课本定义1下的周期函数,定义域D一定是一个无限集,且至少一端无界;课本定义2下的周期函数,其定义域D左右双向无界对称.
事实上,课本定义1下的周期函数要求对任意的x∈D,都有x+T∈D,能推出x+kT∈D,k∈N*.易知当T>0时,定义域在数轴上正向无界,但不能保证“负向无界”;当T<0时,定义域在数轴上负向无界,但不能保证“正向无界”,更不能确定定义域在数轴上双向无界.
课本定义2下的周期函数要求T和-T都是周期,因此当x在定义域D中时,x+T与x-T也在定义域D中,可推知x±kT∈D,k∈N*,这样就要求定义域D是左右双向无界对称的.
命题1当定义域D双向无界时,两个定义等价.
命题1是错误的.修改例1中的案例为:
函数g(x)=1,x∈D,D={n|n=2k,k∈z,k≤0}∪{2,3}∪[4,+∞),对任意的x∈D,易知都有g(x+2)=g(x),但g(x-2)=g(x)不恒成立(令x=3∈D,但1∉D,所以g(3-2)没有意义).
2.2.2函数周期的比较研究
区别2课本定义2下的周期函数的周期只有一种情况:同时具有正、负周期.而课本定义1下的周期函数的周期情况比较复杂,有三种可能:
(Ⅰ)同时具有正、负周期,如函数f(x)=tanx,易知π ,-π 都是它的周期.
(Ⅱ)只有正周期但没有负周期,如函数g(x)=sin 2x,x∈(0,+∞),它的周期集合是{T|T=kπ ,k∈N*},所以函数g(x)只有正周期却没有负周期.
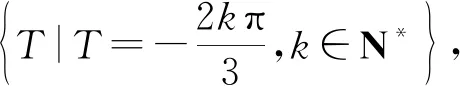
命题2如果T是函数f(x)的一个周期,则nT(n∈Z,但n≠0)都是它的周期.
这是似是而非的一种说法,在许多教学资料中广为流传,我们需要作科学分析:
在课本定义1下,由T是函数f(x)的周期,并不能推出 -T也是一个周期.因此,它是一个假命题.我们只能说:如果T是函数f(x)的一个周期,则nT(n是正整数)都是它的周期.
在课本定义2下,连续运用“±T是f(x)的一个周期”条件k次, 得f(x)=f(x±T)=f[(x±T)±T]=f(x±2T)=…=f(x±kT),k∈N*,可见±kT(k∈N*)均为函数f(x)的周期,这时命题3是真命题.
2.2.3最小正周期与周期关系的比较研究
在两个课本定义下,若周期函数f(x)存在最小正周期T*,则它的任意一个周期T与最小正周期T*的关系如何?
例3函数f(x)=1,x∈{0}∪[2,+∞)是周期函数,其周期的集合为[2,+∞).
解易知f(x+T)=f(x)=1,x∈{0}∪[2,+∞),T≥2,在课本定义1下,函数f(x)是周期函数,其周期的集合为[2,+∞),最小正周期T*=2.

再来研究在课本定义2下,T*与T的关系如何?
结论在课本定义2下,若周期函数f(x)存在最小正周期T*,T是它的任意一个周期,则T=kT*,k∈Z,但k≠0.
证明若T是正周期,且不是T*的正整数倍,则存在n∈N*,使T=nT*+r(0 若T是负周期,类似可证,略. 2.2.4周期函数图象的比较研究 理想的周期函数的图象,应该是均匀地、周而复始地变化的.人们研究“周期性”的意义,就在于只要讨论清楚一个周期内的情况,那么从局部到整体,从有限到无限的所有情况就都清楚了. 课本定义1下的周期函数,只要求f(x+T)=f(x),从图象平移的角度来看,是向左或向右单向移动.而课本定义2下的周期函数,对于定义域D内的任意x,有x±T∈D,还同时要求f(x+T)=f(x)和f(x)=f(x-T)成立,这样前后周期内的图象能来回双向移动,必然完全相同,因而函数f(x)在每个周期内的图象必然是完全一致的. 图1 (1)根据课本定义1,f(x)是周期函数,且有周期T=1(证明略). (2)画出函数f(x)的图象,却没有给我们一种“周而复始”的感觉,不具有周期特征. 容易看出,当n增大时,dn严格单调增加,因此所有线段的长度都不相等.这样沿x轴每隔一个单位(一个周期长1),函数f(x)的图象各不相同. 我们构造出的这个实例,根据课本定义1是周期函数,但从整体上看函数图象不是周而复始的,且每个周期内的图象都不一样.如果将例4中函数向左扩展:f(x)的定义域向左每个周期长度逐个减少一个点,这样得到新的定义域是双向无界的,在课本定义1下仍是周期函数,但每个周期内的图象却完全不相同. 对于课本定义2下的周期函数,如果把握了它的一个周期内的情况,那么也就把握了整个函数的情况,在研究这类周期函数的性态时,可局限在某个周期内进行讨论,因为周期函数的整体性质无非是它在周期内的性质进行周期延拓的结果. 区别4课本定义2下的周期函数的图象,会给人以“周而复始”的直观感;而课本定义1下的周期函数的图象,只要求单向重现,其图象重复出现是有方向性的,从整体上看并不一定有“周而复始”这种感觉. 课本定义1下的周期函数,不一定是课本定义2下的周期函数.如函数f(x)=1,x∈{0}∪(2,+∞),容易证明:在课本定义1下它是周期函数,其周期集合是(2,+∞),没有最小正周期,但在课本定义2下它不是周期函数.而课本定义2下的周期函数,一定也是课本定义1下的周期函数. 什么情况下两种定义能统一?由例4,知定义域双向无界时两种定义不能统一.文献[4]给出了课本定义1下的周期函数f(x),满足如下两种情况之一: (1)定义域D关于某点x=x0对称.(2)同时具有正负周期.则函数f(x)也是课本定义2下的周期函数.特别地,当定义域D=R时,两种定义等价. 周期函数的课本定义1使用范围广泛,影响很大,留下的核心问题:如何判断课本定义1下周期函数的图象是“周而复始”的?只有选用这样的周期函数进行教学,才能让学生把握其本质:知道了函数一个周期内的情况,就能推知整个函数的情况. 两种课本定义下的周期函数能统一时,其图象一定是“周而复始”的,故有: 判定方法1课本定义1下的周期函数f(x)定义域D关于某点x=x0对称,则函数f(x)的图象是周而复始的. 判定方法2课本定义1下的周期函数f(x)同时具有正、负周期,则函数f(x)的图象是周而复始的. 除了以上两种方法,还有定义域直观判断方法: 判定方法3课本定义1下以T为周期的函数f(x),其定义域D是下面四种情况[a,+∞),(a,+∞),(-∞,a],(-∞,a)之一,从左向右如果在第一个周期区间[a,a+T)或(a,a+T](或最后一个周期区间(a+T,a]或[a+T,a))上全部有定义,则函数f(x)的图象是周而复始的. 文献[4]中给出的周期函数严格定义,是课本定义2的局部化应用.可改写为下面比较严谨且简洁的判定方法: 判定方法4函数y=f(x)是定义在D上,在课本定义1下以T为周期的函数,如果对任意的x∈D且x-T∈D,都有f(x-T)=f(x)成立,则函数f(x)的图象是周而复始的. 有兴趣的读者可自行证明,这里略去. 在高中周期函数教学中,只需研究满足定义且具备“周而复始”特性的“理想”的周期函数,掌握这些方法就具有重要的现实意义:高中数学教师在选择周期函数例习题时,能避开有缺陷的“伪”周期函数,更有利于高中周期函数内容的教学.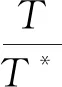
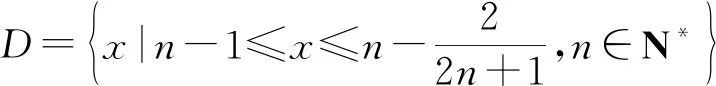

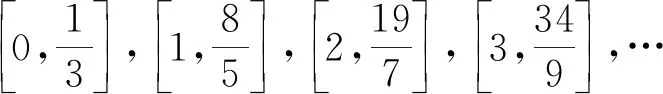
3 两种周期函数关系的比较研究
3.1 两种周期函数的统一
3.2 课本定义1下的周期函数,具有“周而复始”特性的判断

