交变载荷下液压缸非线性动态特性的数值分析方法

陈鹏霏， 和 鹏， 于泰龙， 贺宇新

(1.长春工业大学 机电工程学院， 吉林 长春 130012； 2.长春职业技术学院 机电学院， 吉林 长春 130033)

引言

目前，随着液压驱动装置向高精度、高稳定性方向发展，对其动力学性能的要求也越来越高[1]。同时，由于液压系统的复杂性，其模型通常具有显著的非线性和时变性特征。如何准确、高效地求解非线性动态系统模型，一直是动力学分析领域的研究热点之一[2-3]。

近年来，国内外学者针对液压缸的非线性动力学特性，开展了大量的研究工作。在国外，MAGYAR B等[4]以普通阀控式液压缸系统为研究对象，通过解析方法，分析了时滞及死区等非线性因素对液压定位系统动力学特性的影响，确定了实现系统稳定的参数域。MISRA A等[5]考虑到流体的可压缩性，从液压控制阀角度分析了液压缸非线性运动特性问题，研究了当控制阀相关参数改变时所引起的不同程度的液压自激振动现象。LICSKO G等[6]以流体非线性动力学理论为基础，建立了普通液压系统中单级溢流阀的动态特性数学模型，深入研究了分岔、混沌等动力学现象的产生机理。在国内，陈佳等[7]基于LuGre摩擦模型推导了完整的数字液压缸非线性状态空间模型，并对三种不同工况条件下的模型进行了仿真和试验研究，重点分析了系统换向时的动态特性。王林鸿等[8]研究了非线性摩擦力和液压弹簧力的产生机理，并采用Lienard方程描述二者耦合作用下的液压缸动力学方程，指出方程的解在不同工作条件下具有不同的形态，说明液压缸非线性动态特性复杂多变。姜万录等[9]系统阐述了弹簧力和摩擦力等非线性因素对电液伺服系统动力学特性的影响规律，指出非线性液压弹簧力引起的“跳跃现象”和非线性摩擦力引起的极限环型振荡的共同作用，是导致系统发生非线性振动的一个主要原因。

此外，由于非线性是液压系统中普遍存在的难题。目前已有学者采用较为成熟的非线性振动学理论Duffing方程、Van Der Pol方程和Lienard方程，来解决液压缸的非线性动力学问题，并取得了良好的效果。但是，在模型转化过程中仍不可避免地需要进行相应的简化，影响了模型的求解精度。

因此，本研究以液压缸非线性动态特性为研究对象，深入阐述液压弹簧力和摩擦力的产生机理，揭示其各自体现出的非线性和时变性特征，并通过数值方法离散时间域步长，对交变载荷作用下液压缸的非线性动力学方程，进行数值仿真分析。

1 液压缸动力学模型

液压缸属于液压系统中的执行元件，可将油液压力能转换为机械能输出。虽然液压缸的种类繁多，但其工作原理基本相同。单活塞杆双作用式液压缸的工作原理简图，如图1所示。

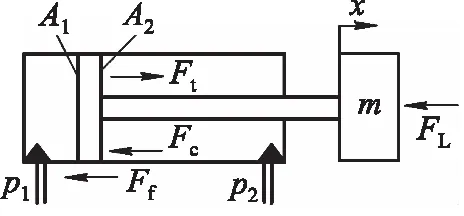
图1 单活塞杆液压缸的工作原理图

若液压油液从左侧无杆腔进入，由右侧有杆腔输出，则活塞杆驱动负载向右伸出。于是，进油腔油液对活塞的有效作用力为F1=p1·A1，回油腔对活塞的有效作用力为F2=p2·A2。这里，p1为进油腔压力，p2为回油腔压力，A1为无杆腔有效面积，A2为有杆腔有效面积。根据图1中的受力分析可知，液压缸左右两腔内油液对活塞的有效作用力，可等效为液压弹簧力Ft，即Ft=p1·A1-p2·A2。

根据牛顿第二定律，其动力学方程可表示为:

(1)

式中，m—— 活塞和负载的等效质量

Fc—— 介质黏性阻尼力

Ff—— 运动过程中的摩擦力

Ft—— 液压弹簧力

FL—— 外加负载

2 非线性时变特征参数分析

2.1 非线性液压弹簧刚度

如图1所示，当液压缸驱动负载向右移动时，有杆腔和无杆腔内均充满了液压油，且都处于压缩状态。因此，总的液压弹簧刚度可看作是两腔产生的液压弹簧刚度并联作用的结果[10]。并且，随着活塞的移动，左右两腔液体弹簧的长度将会发生变化，弹簧刚度随之发生变化。根据胡克定律，可得液压弹簧刚度随活塞位移变化的规律为[8]：

(2)

式中，Ko—— 油液的体积弹性模量

x0—— 活塞的初始位置

L—— 液压缸活塞的总行程

α，γ—— 待定系数

于是，根据式(2)可得液压弹簧刚度k(x)随活塞位移x的变化曲线，如图2所示。当液压缸为α=1，γ=0工况时，表示系统为进油节流且回油路无背压的回路，此时k(x)随行程x增加逐渐变小，全程表现出软弹簧特性；当液压缸为α=1，γ=1工况时，表示系统为进油节流且回油路有背压的回路，此时k(x)随行程x增加，先逐渐变小后又逐渐变大，表现出半程软弹簧半程硬弹簧特性；当液压缸为α=0，γ=1工况时，表示系统为回油节流回路，此时k(x)随行程x增加逐渐变大，全程表现出硬弹簧特性。

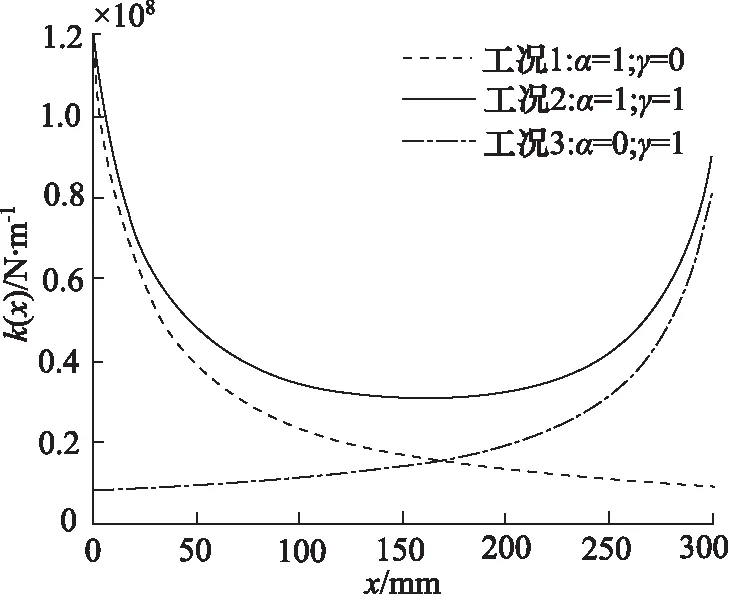
图2 液压缸弹簧刚度的非线性变化规律

由图2可知，液压缸的等效弹簧刚度k(x)随活塞位移x的变化，会呈现出明显的非线性特性。因此，在液压弹簧刚度的影响下，活塞上作用的液压弹簧力Ft也将出现明显的非线性特征。

2.2 时变阻尼特性

由Stribeck摩擦理论可知，液体的润滑状态分为三种主要类型：Ⅰ为边界润滑状态；Ⅱ为混合润滑状态；Ⅲ为流体动压润滑状态。根据Stribeck摩擦理论，可获得摩擦力随速度变化的数学模型为[9]:

(3)

(4)

式中,Ff—— 摩擦力

Ffd—— 动摩擦力

Fe—— 外力

Fj—— 最大静摩擦力

Fk—— 库伦摩擦力

v—— 摩擦副的相对运动速度

vs—— Stribeck速度

B—— 黏滞摩擦系数

τ—— 经验参数，一般在0.5～2之间取值[9]

根据式(3)和式(4)，可获得摩擦力随速度变化的关系曲线，如图3所示。根据图3可知，当工作点位于区域Ⅰ和区域Ⅱ时，摩擦力Ff随速度v非线性变化，且随速度增加，导致摩擦阻尼处于负阻尼状态。而当工作点位于区域Ⅲ时，摩擦力随速度基本发生线性变化，随着速度的增加，摩擦阻尼的作用效果增加了整个系统的阻尼。

图3 摩擦力随速度变化线图

对于液压缸动态系统，受自激振动和受迫振动影响，将导致活塞实际的瞬时速度v会在一定范围内剧烈变化。由图3可知，当瞬时速度v的变化范围跨越不同润滑区域时，必然导致摩擦阻尼随之发生激烈变化。因此，相比液压弹簧刚度在整个行程内的非线性变化，液压缸的摩擦阻尼呈现出明显的时变性特征。

3 液压缸动态数值分析

3.1 交变载荷作用下的动力学分析

根据2节内容可知，在活塞运动过程中，液压弹簧刚度具有非线性特征，而摩擦阻尼具有时变性特征。因此，系统可抽象为如图4所示的模型。

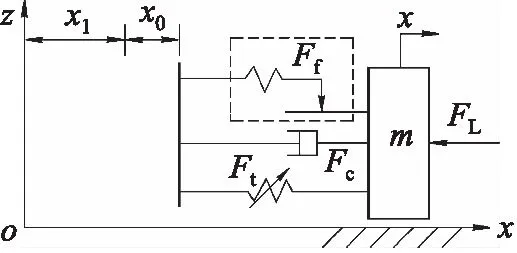
图4 液压缸活塞的非线性动力学模型

如图4所示，当油液驱动活塞运动时，假设输入的油液流量q不变，则理论上活塞的预期运动速度ve=q/A1保持不变。但是，由于实际液体具有可压缩性[11]，需要蓄备油液以便形成液压弹性力。若该工作点处的液压弹簧刚度为k(x)，则产生的液压弹簧力为：

Ft=-k(x)[x-(x0+x1+vt)]

(5)

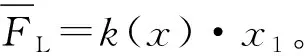
(6)

(7)

式中，c′为摩擦阻尼系数。

液压缸活塞受到的阻尼力可表示为:

(8)

式中，c0为系统阻尼系数。

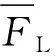
(9)

式中， ΔFL为交变力的变化幅值；ω为交变力的激振频率。

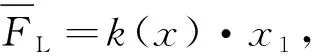
(10)

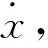
(11)

若将液压等效弹簧刚度k(x)近似表示为常数k，摩擦阻尼系数c′、动静摩擦力之差ΔFf均作为常数处理，则式(11)可简化为二阶常系数非齐次线性微分方程。其全解可由对应的齐次线性微分方程的通解和非齐次线性微分方程的特解构成。

3.2 非齐次线性微分方程的求解

根据线性微分方程理论，式(11)对应的齐次线性微分方程为:

(12)

列出式(12)的特征方程，求得其通解形式为:

xT=e-ξω0t(Asinω0t+Bcosω0t)

(13)

式中，A和B为待定系数。

依据叠加原理，式(11)等号右侧函数可表示为f1(t) 和f2(t)之和的形式。即:

(14)

(15)

对于函数f1(t)，由线性微分方程理论可知其特解形式为:

x1=at+b

(16)

式中，a和b为待定系数。将式(16)代入由式(14)构成的非齐次线性微分方程，可解得a=ve；b=(ΔFf-c0ve)/k。

对于函数f2(t)，假设激振频率不等于固有频率，即ω≠ω0，则±iω不是特征方程的根。由线性微分方程理论可知其特解形式为:

x2=hsin(ωt-ε)

(17)

式中，h和ε为待定系数。将式(17)及其一阶和二阶偏导数，代入由式(15)构成的非齐次线性微分方程，可解得待定系数h和ε分别为:

(18)

于是，二阶常系数非齐次线性微分方程式(11)的位移全解x为：

x=xT+x1+x2=e-ξω0t(Asinω0t+Bcosω0t)+vet-

(19)

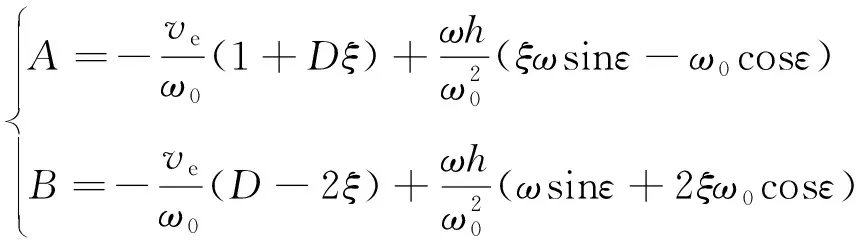
(20)

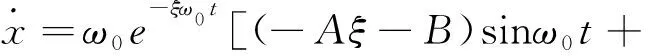
(-Bξ+A)cosω0t]+ve+hωcos(ωt-ε)

(21)

3.3 非线性微分方程的数值分析方法

由2节中的分析结论可知，在影响液压缸非线性动态特性的因素中，液压弹簧刚度主要呈现出非线性特性；而摩擦阻尼则主要呈现出显著的时变特性。因此，在对液压缸动态特性进行数值分析过程中，可以采取离散时间段的方法，将活塞完成整个行程所需的时间t离散成n段[13]。

对于液压弹簧刚度，尽管其在整个行程范围内是非线性的(如图2所示)，但当n→∞时，在时间段Δti=ti-ti-1(i=1,…,n)内，液压弹簧刚度可近似看做线性变化。根据式(2)，在时间段Δti内液压弹簧刚度可表示为:

(22)

式中,xi为ti时刻活塞所处的行程位置；xi-1为ti-1时刻活塞所处的行程位置。

对于摩擦阻尼，其在整个行程中体现出的是明显的时变性特征。因此，根据Taylor展开法，将摩擦力在工作点处线性展开，忽略高阶微分量，则在时间段Δti内摩擦阻尼可表示为:

(23)

动静摩擦力之差可表示为:

(24)

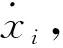
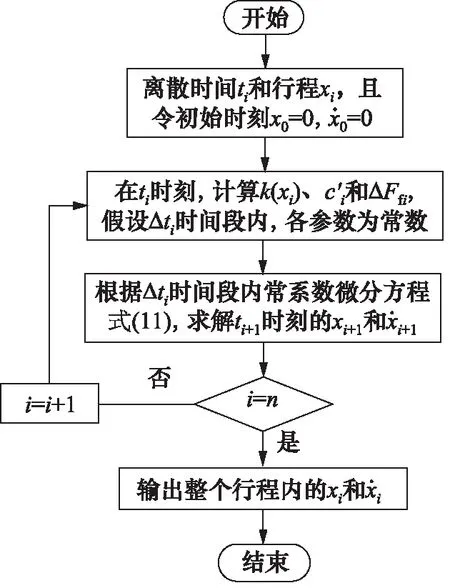
图5 数值分析流程图

4 数值分析实例

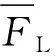
基于上述数值分析方法，假设40 ℃时由于黏性产生的系统阻尼[14]c0为3.839×103N·s/m，且液压缸的预期驱动速度ve=3 mm/s时，其活塞运动瞬时速度的时域图像，如图6所示。

图6 交变载荷作用下活塞瞬时速度的时域图像

一般来说，第一部分自激振动过程由于系统阻尼的存在，很快就衰减了，因此比较短暂。但是，当活塞的预期运动速度ve不同时，会导致运动处于不同的润滑区域，从而造成活塞在自激振动过程中产生不同的运动结果。预期运动速度ve不同时，即不同润滑状态下活塞瞬时速度的时域图像，如图7所示。

如图7a所示，当预期速度为2 mm/s时，活塞瞬时速度将在边界润滑区域Ⅰ和混合润滑区域Ⅱ内不断变换(如图3所示)，此时摩擦阻尼将体现出负阻尼特性，即随着活塞瞬时速度增大，摩擦力会减小，从而导致阻尼比ξ较小，甚至为负值(ξ<0)。因此，活塞在很长一段运动行程内速度振动得不到衰减，出现时缓时急的液压爬行现象。

如图7b所示，当预期速度为3 mm/s时，活塞瞬时速度基本在流体动压润滑区域Ⅲ和混合润滑区域Ⅱ内变换(如图3所示)，此时摩擦阻尼主要体现出的是正阻尼特性(ξ>0)，即随着活塞瞬时速度的增大，摩擦力增大。偶尔，摩擦阻尼会导致负阻尼现象[15](ξ<0)。因此，液压缸活塞仅在整个行程的初始处，出现了短暂的液压爬行现象，随即便迅速衰减为等速运动。并且，在衰减过程中，由于偶尔负阻尼现象导致速度的时域图像中出现波形复杂、尖峰较多的现象。其位移x的时域图像如图9a所示。

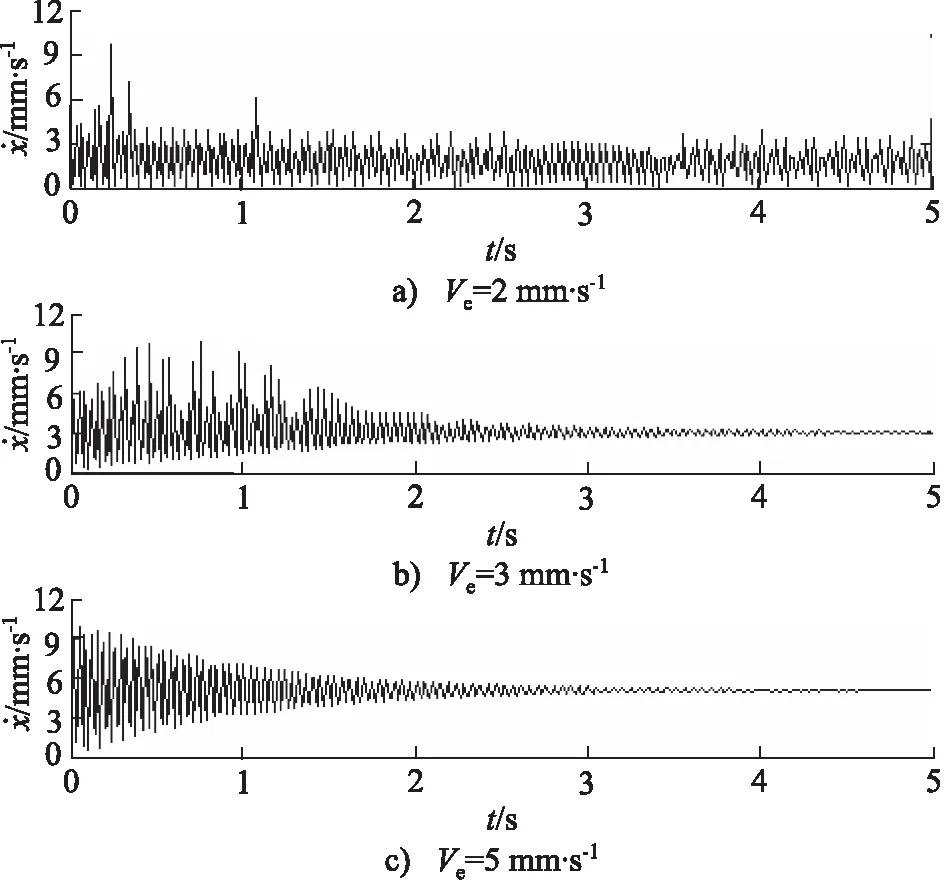
图7 不同条件下活塞瞬时速度自激振动部分的时域图像

如图7c所示，当预期速度为5 mm/s时，活塞瞬时速度基本均处于流体动压润滑区域Ⅲ内，此时摩擦阻尼体现出的是正阻尼特性(ξ>0)，即随着活塞瞬时速度的增大，摩擦力将增大。于是，活塞仅在行程的初始处出现了短暂的液压爬行现象，随即迅速衰减为等速运动。并且，若阻尼比ξ越大，其衰减过程越快。

活塞瞬时速度的第二部分，是按受迫振动的规律进行振动。由式(17)可知，受简谐激振力FL作用的影响，受迫振动仍然是简谐振动。其振动频率等于激振力FL的频率ω；其振幅表达式可见式(18)。由式(18)可知，受迫振动的振幅h不仅与激振力的力幅ΔFL有关，还与激振力的频率ω以及整个系统的质量m、液压弹簧刚度k(x)和阻尼比ξ有关。当激振力频率ω和系统阻尼系数c0取不同值时，即在不同条件下活塞瞬时速度受迫振动部分的时域图像，如图8所示。

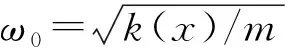
图8 不同条件下活塞瞬时速度受迫振动部分的时域图像

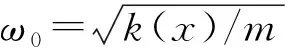
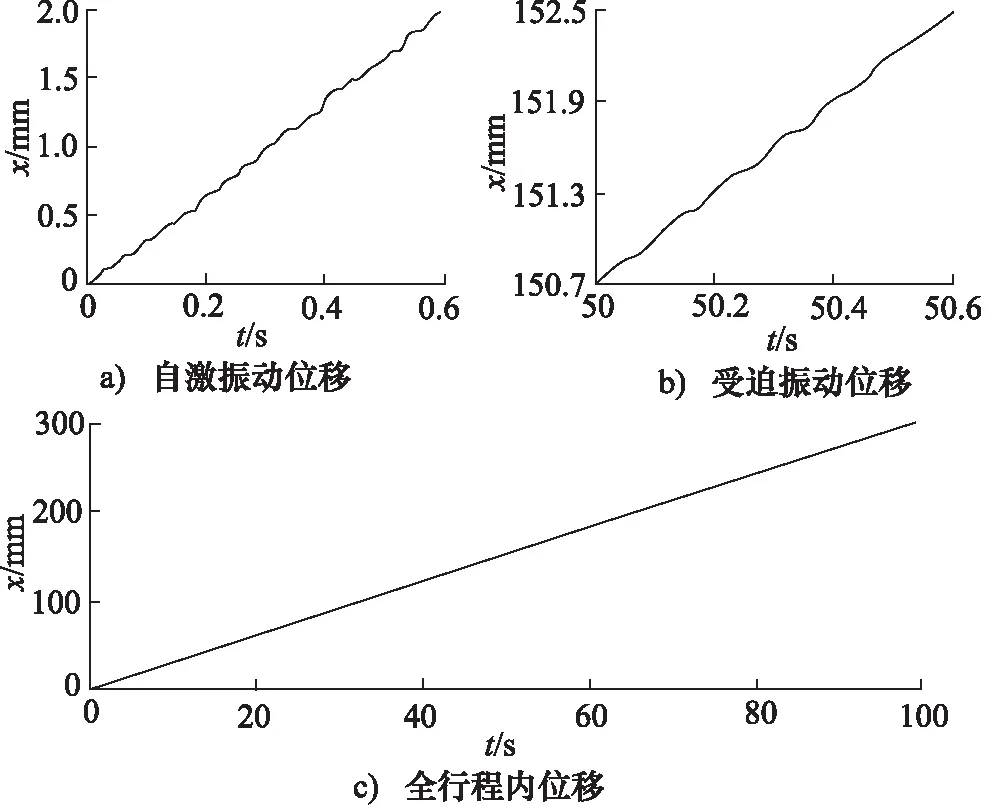
图9 交变载荷下液压缸活塞的位移时域图像

如图8c所示，当激振频率ω为65 rad/s ，系统阻尼系数c0增加为3.839×105N·s/m时，虽然激振频率ω与固有频率ω0间距离变小，导致系统存在共振趋势，但是由于提高系统阻尼的缘故，因此活塞速度的振幅被有效抑制，并未明显增加。

液压缸活塞的位移时域图像，如图9所示。这里，预期速度为3 mm/s，激振频率ω为65 rad/s ，系统阻尼系数c0为3.839×103N·s/m。行程初始时的液压爬行现象，主要由自激振动原因造成，相应的位移时域图像，如图9a所示。行程至中间位置时的液压爬行现象，主要由受迫振动原因造成，相应的位移时域图像，如图9b所示。活塞在整个行程内的位移时域图像，如图9c所示。

5 结论

(1) 对于液压缸驱动系统而言，在活塞运动的整个行程内，液压弹簧刚度主要体现出非线性特征；而摩擦力由于随速度变化频繁，主要体现出明显的时变性特征；

(2) 采用离散时间的方法，对液压缸的动态特性进行数值仿真分析，结果表明与实际测试中出现的速度时域波形复杂、尖峰繁多等现象基本相符，能够较好地分析液压缸的动态特性；

(3) 对于交变载荷作用下的液压缸驱动系统，当激振频率远远小于或远远大于固有频率时，均可忽略系统阻尼对其动态特性的影响；当激振频率接近固有频率时，系统阻尼对其动态特性影响显著。