基于模糊数据挖掘的灌区水资源配置研究

包志炎 郑高安 王 萱 邱 雁 魏 杰

(1.浙江水利水电学院计算机应用技术研究所， 杭州 310018; 2.浙江省水利信息管理中心， 杭州 310009;3.杭州钱塘新区建设投资集团有限公司， 杭州 311228)

0 引言

随着社会经济的发展、人口的增加以及人类对水资源需求的提高，水资源日益短缺。预计到2050年，全球人口将增长到95亿，届时粮食需增产60%、农业用水量需增加19%，才能满足基本需求[1]。中国是农业大国，农业是最主要的用水部门。在区域水资源配置时，农业与工业、生活、服务业等其他行业一起参与用水分配。保障国家粮食安全，核心在灌区。灌区以占全国耕地49%的面积，生产了约占全国总量75%的粮食和90%以上的经济作物[2]。因此，加强灌区水资源配置研究，科学、合理、有计划、有重点地用水显得尤为重要和迫切。

目前，国内外灌区水资源配置方法主要包括规划优化、系统模拟和智能计算。规划优化方法基于数学规划理论，在既定约束条件下，面向单目标[3-5]或多目标[6-9]实现，在多种方案中寻求最优方案，较为常用的有线性规划[10]、动态规划[7-8,11]和随机规划[12-13]等，该方法需要构造较为复杂的目标函数和严格的约束条件。系统模拟方法既有面向农田的作物全生育期需水量模型[14-15]，也有面向区域、灌区的分布式水循环模型[16-17]和水文模型[18-19]，需要模拟灌区水资源系统内部的复杂关系。智能计算方法将粗糙集、神经网络[20]、粒子群算法[21]、果蝇算法[22]、人工鱼群[23]等算法应用于灌区水资源配置中，需要进行收敛性分析，有时会出现局部最优解。数据挖掘侧重关联分析，不必进行严格的逻辑推理和收敛分析，从而能避开复杂的目标函数建模和边界条件分析过程，实现从海量数据中抽取感兴趣的、隐含的、有价值的知识，是当前水资源预测理论发展的重要趋势之一。EKASINGH等[24]基于数据挖掘建立了灌区农作物选择规则；THOMPSON等[25]和MOHAN等[26]利用数据挖掘改进水资源日常管理，将决策过程简单化；SHAHANAS等[27]提出了智能水管理的技术架构。随着我国水资源监控能力建设项目的实施[28]，全国各地水资源感知监测体系不断完善，灌区数据资源日益丰富，为数据挖掘在水资源配置中的应用创造了条件。蒋云钟等[29]提出了水资源数据挖掘的体系框架，刘予伟等[30]在分析水资源大数据采集的基础上提出构建水资源大数据云平台的思想，杨小柳等[31]基于数据挖掘提出节水的精准化、差异化管理。目前的相关研究更多侧重于理论框架和设想建议。本文基于数据挖掘，融合相关性分析、聚类分析、相似性度量等算法，对浙江省行政区域行业间配水进行特征分析，对中型灌区需水量进行预测，为科学合理配水提供决策支持。

1 灌区数据资源

构建灌区大数据，汇聚足够丰富的高质量灌区水资源数据资源是开展数据挖掘的前提。灌区数据资源既包括灌区占地、工程设施、作物种植结构等基本数据，也包括所在行政区域水资源、经济、人口、水文、气象等相关数据；既包括实时监测数据，也包括历年用水数据，如表1所示。表中数据均可以从区域水文、水资源、经济发展的统计年报或灌区感知监测数据库中获取。

表1 灌区数据资源构成Tab.1 Data resources of irrigation area

2 面向灌区水资源配置的数据挖掘方法

2.1 区域行业间配水聚类分析

以行政区域为研究单元，当区域可供水量不能满足所需水量时，既要强调农业用水的基础性，又要保障区域社会经济目标实现。因此，在不同行业、不同部门之间就会产生竞争用水问题。由于区域间经济发展水平、产业结构和资源禀赋不一，各行业用水需求差异较大。在有限的区域水资源条件下，需要解决行业间如何合理配水问题。

针对某省所有行政区域，汇聚工业、生活以及生态环境等领域的历年用水数据，聚焦农业灌溉用水，引入模糊聚类算法，对区域行业配水案例进行聚类分析，从中发现同类区域行业配水的显著特征，为管理者开展区域行业间配水提供决策支持。区域行业配水聚类分析流程如下：

(1)建立行业配水案例集。假设某省共有n个市级行政区，选取m个能反映某一时期在农业、工业、生活和生态等领域用水的相关指标，建立由n个区域行业配水案例组成的案例集，以各案例的指标值为内容构造数据矩阵

(1)

(2)标准化数据矩阵。为消除各参数间不同量纲的偏差，通过“平移-标准差-极差”变换[32]将数据转换到[0,1]区间，进行数据标准化，计算得到矩阵

A′=[a′ij]n×m

(2)

其中

(3)计算模糊相似矩阵。为了定量地进行分类，引入夹角余弦相关系数作为聚类统计量，将矩阵A′转换为一个模糊相似矩阵

(3)

(4)配水案例聚类分析。用平方法求A″的传递闭包t(A″)。使用λ-截矩阵，使阈值λ由1减小到0，则t(A″)的分类由细变粗，形成一个动态的聚类图。根据λ的不同取值，可以得到不同分类。λ取值应遵循“类间案例相似性最小化，类内案例相似性最大化”原则，分类过细或过粗均不利于共性特征提取，一般可分为2～4类，且应避免出现类间距的突变[32]。在得到区域行业间配水的类别分组后，即可分析归入同一类的显著特征。

2.2 灌区配水相似实例匹配算法

灌区可供水量与该灌区所在区域降水、地表水、地下水、耗水以及其他行业竞争用水相关。灌区需水量与灌区类型、面积、种植结构等相关。在有限的区域水资源条件下，面向不同特征的灌区，需要解决灌区间如何合理配水问题。

以灌区为研究对象，建立一批典型灌区，汇聚其历年可供水量、需水量的相关数据，形成灌区配水案例集。对于预先给定的一个新灌区(或改造灌区)，在灌区配水案例集中匹配出最相似灌区，为该灌区配水提供决策支持。

(1)建立灌区配水案例集。假设共有n个典型灌区，选取m个与可供水量、需水量相关的指标，建立由n个灌区配水案例组成的案例集，以各案例的指标值为内容构造数据矩阵B，待估灌区记为bx，即

(4)

bx=(bx1,bx2,…,bxm)

(5)

(2)计算差异矩阵。对B的行(每一案例)与bx进行差运算，并进行归一化处理，计算得到其差异矩阵

(6)

(3)确定参数权重。权重反映某参数对于目标指标的重要程度。以灌区需水量为预测指标，确定其他各参数的权重。通过对各参数权重在[0,1]区间内按一定的步长穷举，使用穷举权重，把每一个灌区视作新灌区，用剩余的n-1个灌区预测需水量，并与实际值对比。当相对误差均在预先设定的范围内时，此时权重即为所求的解。若有两个及以上的解，相对误差总和最小的为最优解[33]。当灌区配水案例集发生变化，权重会随着更新，这样的赋权方法实现了动态赋权，且具有客观性。权重向量记为w=(w1,w2,…,wm)。

(4)获取相似实例。考虑到各参数之间的权重差异,引入加权的欧氏距离，计算新灌区与其他灌区间的相似度S(bx,bi),最大相似度所对应的灌区即为所求相似灌区。如果将相似度进行降序排序，可以获取排名靠前的若干灌区组成相似实例组。相似度计算式为

(7)

式中wj——第j个参数权重

2.3 基于实例推理的灌区需水量预测

修正2.2节获取的相似实例(或相似实例组)的需水量，可预测新灌区需水量。两种修正算法如下：

构造加权影响因子法，计算式为

(8)

式中Rx——新灌区需水量

Ri——相似灌区需水量

指数平滑法，计算式为

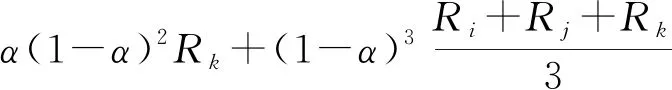
(9)

式中Rj、Rk——相似实例组成员的需水量

α——平滑系数，其取值方法详见文献[34]

3 应用案例

浙江省目前拥有150个大中型灌区，分布在11个市行政区域，其中中Ⅰ型灌区91个，中Ⅱ型灌区48个，大型灌区11个。表2为2018年浙江省各市工业、农业、城镇公共、居民生活以及生态环境等领域配水数据；表3为2018年金华、丽水、衢州、台州、温州等地区部分中型灌区可供水量、毛需水量的相关数据。按灌区规模，分别用数字1～4表示小型、中Ⅰ型、中Ⅱ型和大型灌区。为方便说明问题，以乌溪江引水灌区、横锦水库灌区、罗岙水库灌区作为待估灌区，如表4所示，运用本文建立的方法，分析浙江区域行业配水特征，匹配每一个待求灌区的相似灌区，并在此基础上预测其毛需水量。

基于表2，建立2018年浙江省各市行政区域行业配水案例集，构造相应的数据矩阵

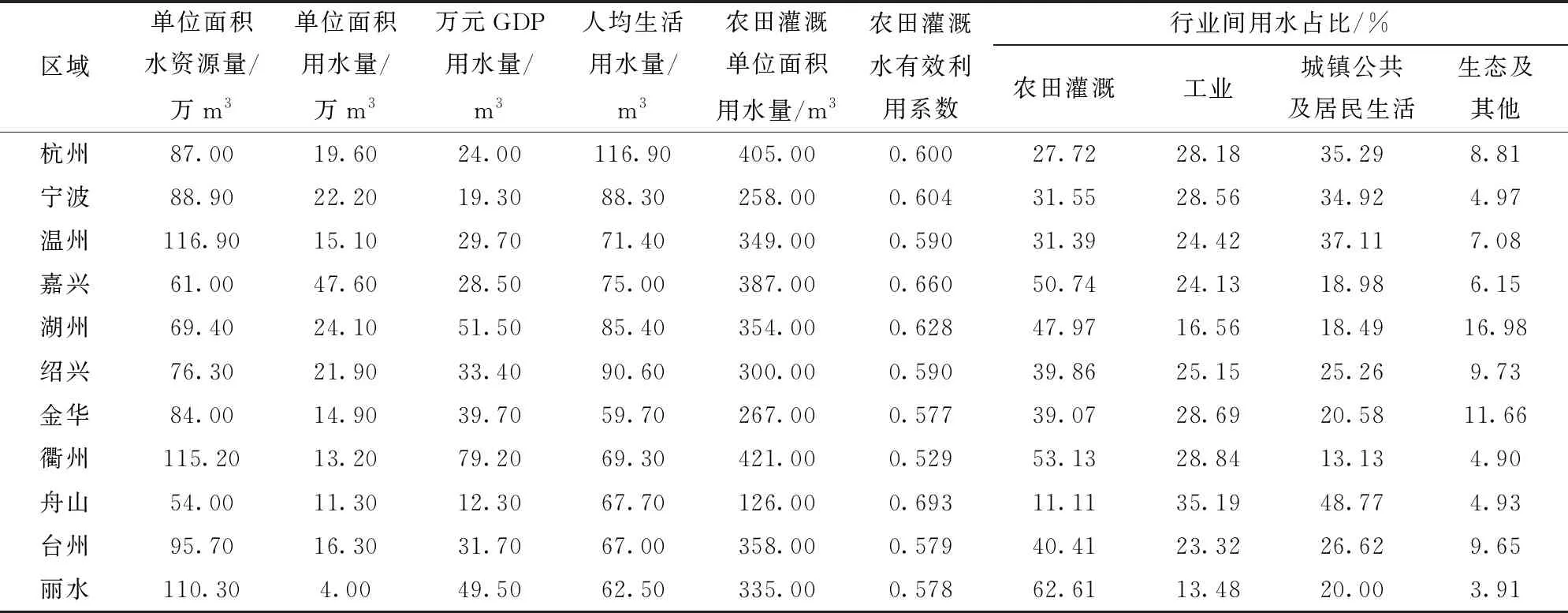
表2 2018年浙江省各市行政区域行业配水量Tab.2 Department water distribution cases in administrative regions of Zhejiang in 2018

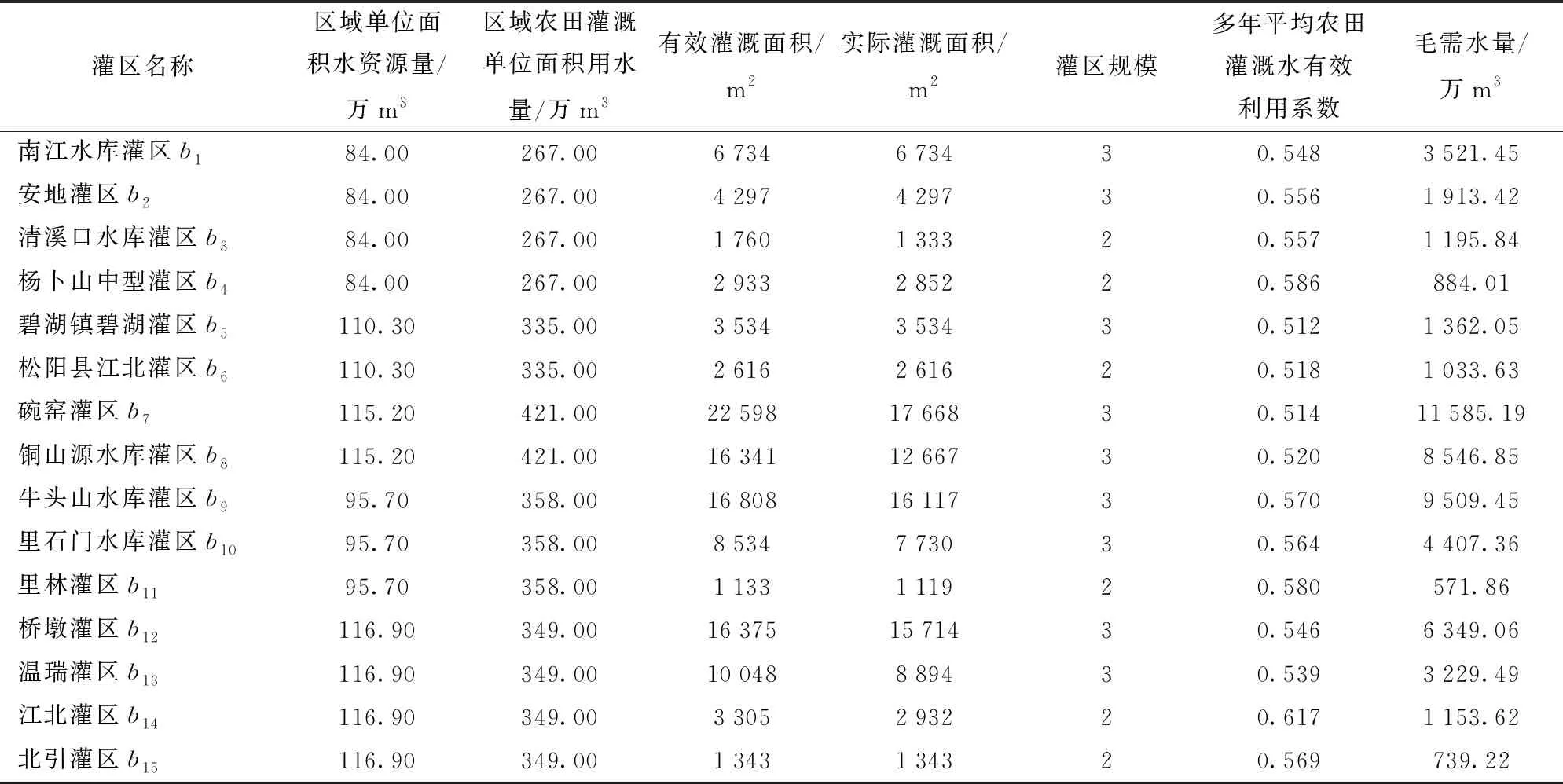
表3 2018年浙江典型中型灌区配水量Tab.3 Water distribution cases of typical medium-sized irrigation areas of Zhejiang in 2018

表4 待估灌区参数Tab.4 Parameters of irrigated area to be estimated

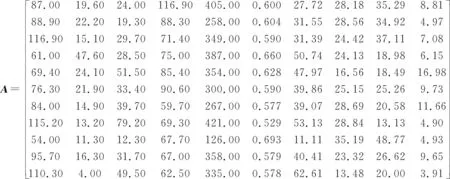
归一化后，计算得到模糊相似矩阵

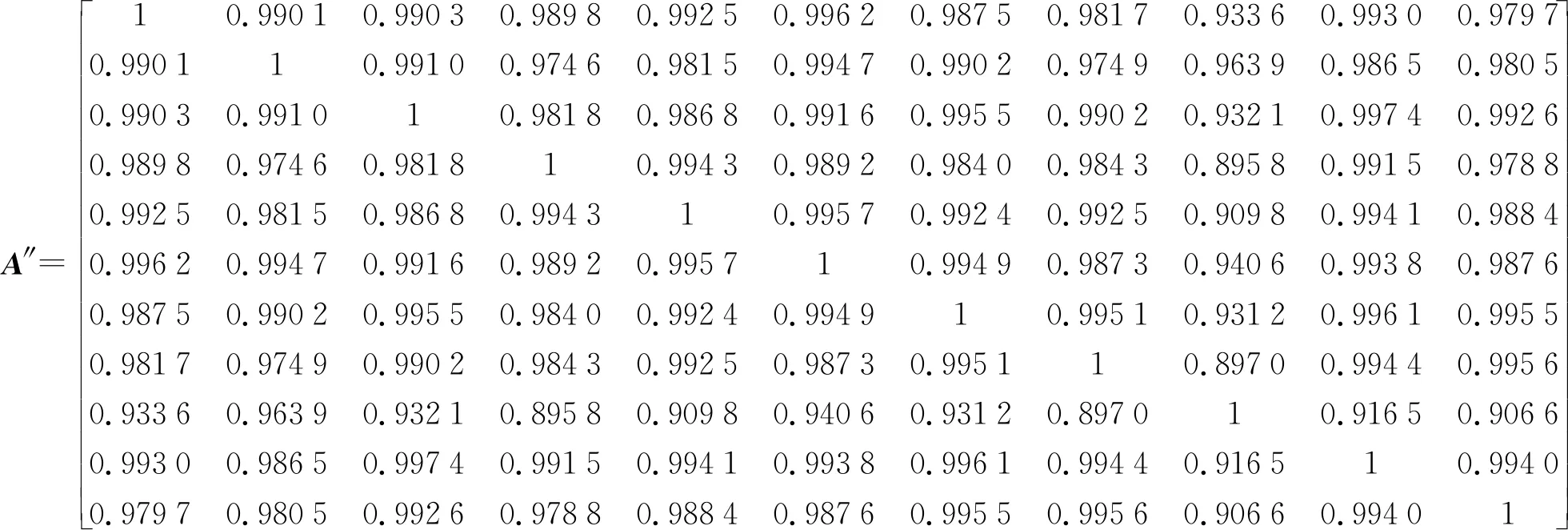
按2.1节的聚类算法，生成动态聚类图，如图1所示。由图可知，当阈值λ=0.994、0.992、0.987时，案例分别被划分为5、4、2类，考虑到在0.992之前类间距约为0.002，下一个值将出现0.005的较大间距，因此λ取0.992。

当λ=0.992时，各市行政区配水被分为4个组别：Ⅰ类{丽水，衢州，金华，台州，温州}，Ⅱ类{湖州，嘉兴 }，Ⅲ类{绍兴，宁波，杭州}，Ⅳ类{舟山} 。可见，Ⅰ类地区单位面积水资源量高，农田灌溉水有效利用系数较低，万元GDP用水量偏高；Ⅱ类地区单位面积水资源量较少，农业用水占比最高，单位面积用水量偏高；Ⅲ类地区工农业用水基本相当，万元GDP用水量处于较低水平，人均生活用水、城镇公共及居民生活用水偏高；Ⅳ类地区单位面积水资源量和用水量均处于最低水平，农业用水占比也最低。

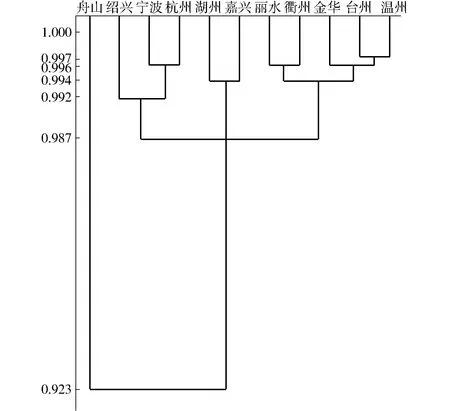
图1 区域配水动态聚类图Fig.1 Dynamic cluster view of regional water allocation cases

基于表3，建立2018年浙江部分灌区配水案例集，构造相应的数据矩阵

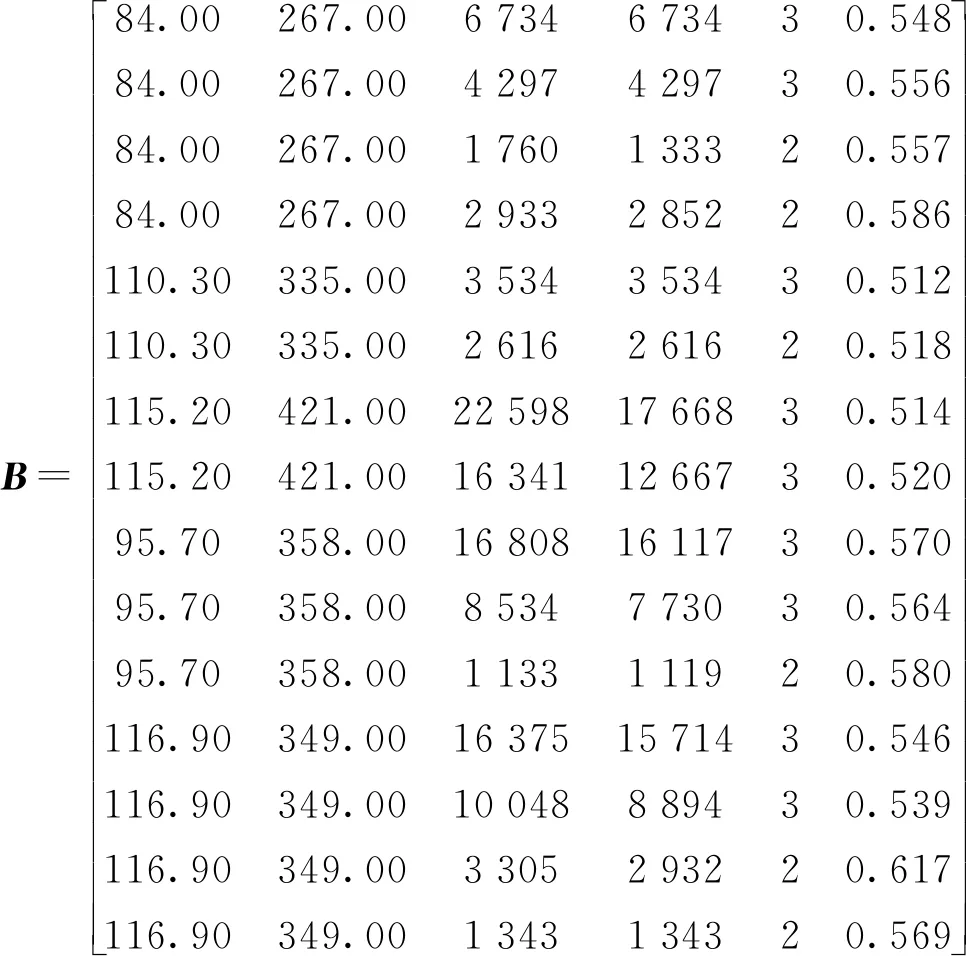
待估的3个灌区分别记为

bx1=(115.20,421.00,17 048,14 061,3,0.494)bx2=(84.00,267.00,7 160,6 374,3,0.547)bx3=(95.70,358.00,947,845,2,0.558)

以罗岙水库灌区为例，计算B的差异矩阵

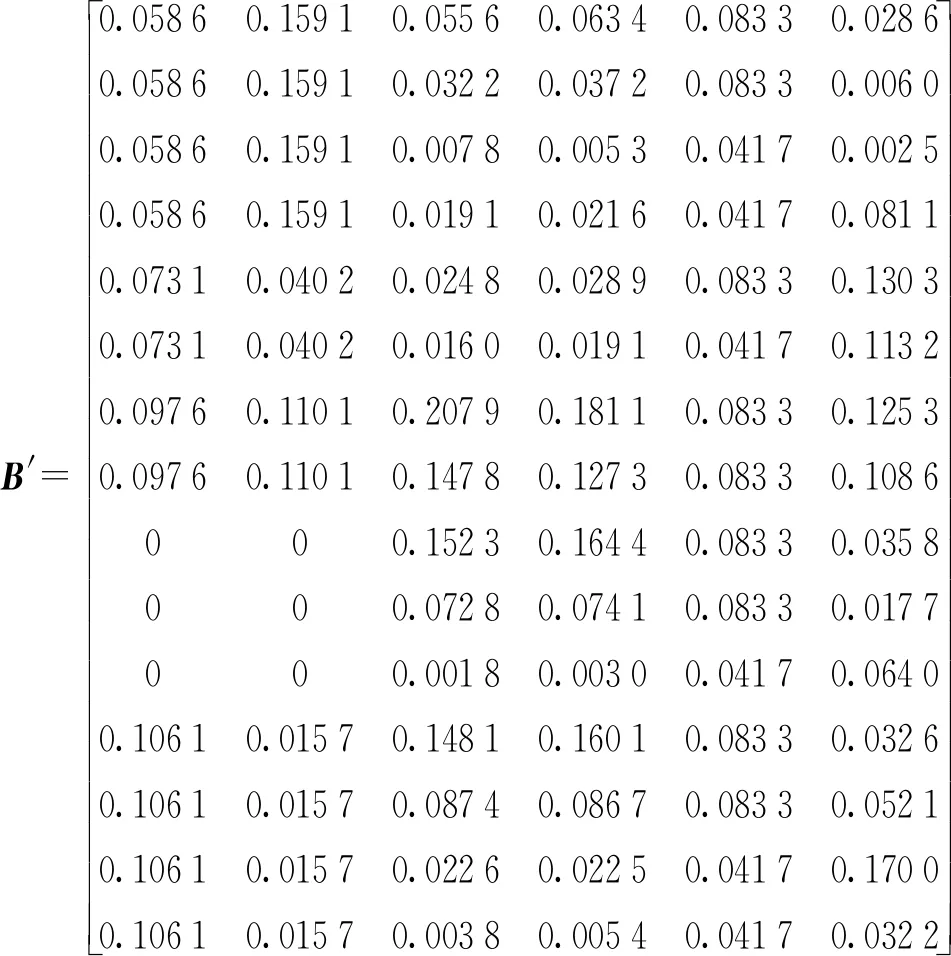
按2.2节权重动态赋权法，以灌区需水量为预测指标，取固定步长为0.01穷举权重组合，设定相对误差阈值为15%，可计算得到权重向量w=(0.05,0.20,0.25,0.35,0.10,0.05)。

采用加权欧氏距离，按式(7)计算待估灌区与其他灌区间的相似度，结果如表5所示。由此，可得到bx1(乌溪江引水灌区)、bx2(横锦水库灌区)、bx3(罗岙水库灌区)的相似灌区分别为b8(铜山源水库灌区，相似度为0.990 5)、b1(南江水库灌区，相似度为0.991 4)、b11(里林灌区，相似度为0.994 6)。

表5 相似度S(bx,bi)计算结果Tab.5 Similarity calculation results

因灌区配水案例集中成员较少，不宜采用指数平滑法，选择构造加权影响因子法，按式(8)计算待估灌区的毛需水量，结果如表6所示，相对误差均不大于9.39%，说明本文方法有效。

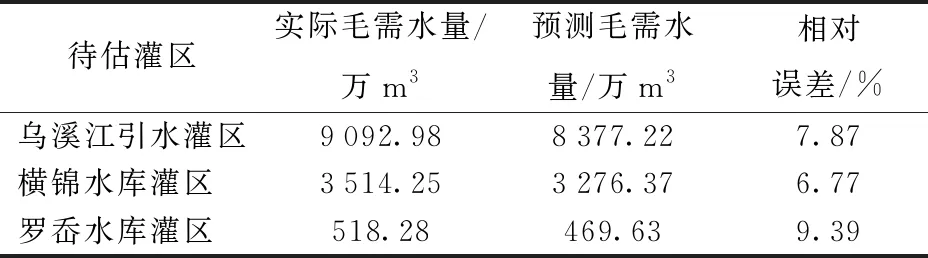
表6 需水量估算结果Tab.6 Water demand estimation results

需要指出的是，合理选择典型灌区，建立有效的灌区配水案例集是实现科学预测的前提。当案例集中灌区案例不够丰富，案例指标值分布不合理，未能覆盖待估灌区的行政区域或类似灌区规模时，待估灌区往往无法获取到足够相似的历史灌区案例，预测结果也会不理想。

4 结论

(1)针对行政区域行业间配水问题，汇聚区域水资源、经济、人口、行业用水等数据，聚焦农业灌溉用水，运用模糊聚类分析，构建区域水资源行业配水案例分类及特征分析模型，并应用于2018年浙江省各市行业配水案例分析。结果显示，浙江省不同区域行业间配水被划分为4类，均呈现出较明显的特征。

(2)针对灌区需水量预测问题，采用固定步长穷举法对灌区配水相关参数进行动态赋权，运用模糊距离匹配相似灌区，通过构造加权影响因子和采用指数平滑法，对基于实例推理的灌区进行需水量预测，并将该方法应用于2018年浙江省中型灌区的需水量预测，预测相对误差均不大于9.39%，验证了方法的有效性。

(3)与规划优化、系统模拟和智能计算等其他水资源配置方法相比，本文方法基于模糊数据挖掘，可以对各类数据直接进行相关分析，避开了复杂的函数建模、边界条件设置和收敛性分析等过程，运用相对简单、易行。但也存在一定局限性：要求涉及相关指标可量化，且各指标已经汇聚相对比较丰富的历史数据；因数据挖掘结果反映的是相关关系，未经严格逻辑验证，存在不确定性，需要在实际应用中不断验证。