基于有限元法的罐内气体空间浓度分布模拟

梁颖

摘      要： 针对罐内储液在气体空间内连续扩散的问题，结合有限元容积法，利用多组分摩尔流的扩散方程及其特殊的边界条件，使用稳定的差分格式将扩散方程简化为对角矩阵，借助于vb6.0语言建立浓度计算的程序界面，得到罐内气体空间的浓度连续分布结果。结果表明：罐内气体浓度绝大多数情况下并不是饱和的，在高度方向上浓度变化有一明显的拐点。本文提出的模型，可以得出任意位置、任意时刻的精确浓度值，模拟结果与实测值的最大误差不超过18.5%。

关  键  词：储罐;浓度分布;有限元;数值模拟

中图分类号：TQ021.4       文献标识码： A       文章编号： 1671-0460（2020）04-0732-06

Abstract： Aiming at the problem of continuous diffusion of the liquid in the gas space of tank， combined with the finite element volume method， the diffusion equation of multi-component molar flow and its special boundary conditions were used to simplify the diffusion equation into a diagonal matrix using a stable difference scheme， and the continuous distribution result of gas concentration in the tank was obtained by program interface for concentration calculation with the help of vb6.0 language. The result shows that the gas concentration in the tank is not saturated in most the time， its facility to make out an obvious inflection point in the direction of height. The exact concentration can be obtained at any position or any time， and the maximum error between the simulation result and the measured value is not more than 18.5%.

Key words： Tank; Concentration distribution; FEM; Numerical simulation

储罐是石油、化工等行业的重要基础设施，由于工艺及技术的限制，存储介质中的轻质组分时刻都在发生蒸发损失，导致罐内气体空间压力增大，当压力增大到一定程度，便通过罐顶的呼气阀排出，造成大气污染。罐内气体空间浓度分布的模型建立，能够实现污染气体排放浓度的在线监测，对掌握罐内存储现状、降低污染气体的排放都具有重要的意义。

由于从数学的角度综合考虑非稳态浓度变化较为困难，之前的理论与实验研究都将气体空间各个位置、各个时段的浓度统一按照饱和浓度处理[1-3]，这样的结果偏于安全，但与气体基本规律扩散并不相符。许多研究是预测扩散通量或者数据的反演分析浓度变化规律，并未提出扩散后浓度的具体计算方法[4-8]。一部分研究者使用MS多粒子交叉耦合数值模型，在实际流体的离子扩散中，对扩散通量与浓度之间的非线性关系，并未给出确定的定解条件，因此未获得准确的定量定性关系[9-12]。王兆利等在建立湍流模型的过程中，未考虑外界温度对于浓度扩散速率的影响[13]。

本研究依据 Maxwell-Stefan扩散方程，确立边界条件，利用傅里叶分析法对差分格式的稳定性进行校核，选择隐式差分格式化简微分方程，使用向前消去法求解具体数值。用离散化的办法对时间、空间进行网格划分，借助vb程序语言的编写实现浓度求解，与实测数据对比说明其稳定性，利用数值结论分析罐体气体空间的浓度分布特点。

1  模型建立

1.1  數理模型的建立

罐内气体空间的浓度与储液性质（温度、饱和蒸气压）、装满系数、存储时间、环境温度、罐体的传热系数等因素密切相关。

由于罐体内部的物质组分复杂导致扩散系数为一变量，且与它的组分相关，依据 Maxwell-Stefan 扩散方程，引入多组分扩散系数，即单位时间内某一定浓度的物质，沿着正交于浓度梯度方向的单位面积上的流通量。以下B表示罐内存储物质，A表示罐内气体空间的空气：

3  实验验证

为了证明本文模型的合理性，对一个固定顶罐（直径 D=0.8 m、罐高 H=1.4 m）进行呼气浓度连续的实验测定，将其与数值模拟结果进行校对。罐内装有汽油，装满度75%，使用外部加热设备模拟日光的热量辐射扩散，利用温度巡检仪测定罐体内外空气、油气、储液不同高度位置处的温度。

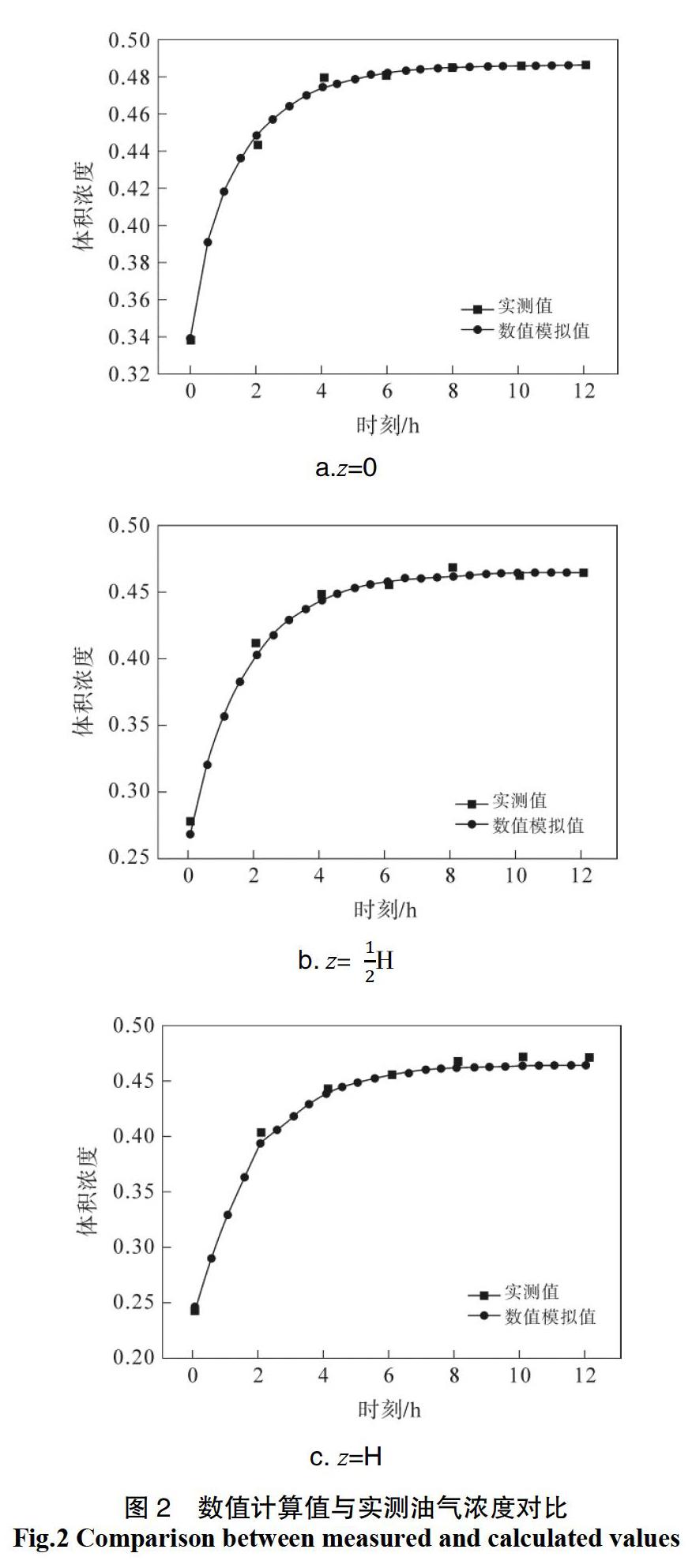
由于罐内气体的扩散没有受到外来气流的影响，属于自由扩散，大气温度随着气体空间平均温度的变化而变化，从数值上基本符合余弦函数的变化趋势[1]，最高温度出现在午后2时-3时，最低温度在临近日出时出现[14]。故模拟临近日出的温度为实验起始，连续测定12 h之内如下位置：油面处（z=0），气体空间高度中间处（z=1/2H）、呼气阀附近处（z=H）的油气浓度。采用岛津气相色谱仪2010-Plus分析得到油气浓度的实测值，将其与数值方法计算的数值进行对比，结果如图2。

由图 2 可见，随着气体空间高度的增加，浓度逐渐降低，在非定常模型下的计算结果显示，罐内气体空间浓度平均5 h后趋于平稳，此后数值拟合程度较高。与实测值相比模拟误差值不超过18.5%。在罐顶位置处，偏差值稍大，考虑罐顶位置处太阳辐射热传热效率的不同，气体在高温时较为稀薄，对外界环境的敏感性较高，浓度变化强度较弱的缘故。但是总体变化趋势一致，模拟值与实测值吻合良好，符合多组分扩散规律。

本方法计算的结果，相比其他计算办法视气体浓度为均一饱和[15]，计算平均误差降低了74.67%。这主要是由于罐内介质扩散速度受到罐体自身与外部操作、气候等条件的影响，浓度变化处于非稳态状态下，因此在整个存储周期内常常是不饱和的。该结果证实此数值模型建立合理，程序窗体设计正确有效，能够有效提高计算精度。

4  实体油罐的模拟结果与分析

选择郑州地区一座地上拱顶油罐为例，内装车用汽油，油罐的直径22.7 m，高12.3 m[16]。（1）一月测得的大气平均最高温度7.2 ℃，平均最低温度-5.7 ℃。气体空间最高温度13.5 ℃，最低温度-2.6 ℃。此时汽油饱和蒸气压为26.8 kPa。（2）三月测得的大气平均最高温度18.4 ℃，平均最低温度5.2 ℃。气体空间最高温度25.1 ℃，最低温度5.3 ℃。此时汽油饱和蒸气压为44.7 kPa。（3）六月测得的大气平均最高温度33.0 ℃，平均最低温度20.8 ℃。气体空间最高温度47.6 ℃，最低温度18.5 ℃。此时汽油饱和蒸气压为83.5 kPa。（4）七月测得的大气平均最高温度36.8 ℃，平均最低温度27.3 ℃。气体空间最高温度51.3 ℃，最低温度25.3 ℃。此时汽油饱和蒸气压为97.9 kPa。（5）八月测得的大气平均最高温度30.9 ℃，平均最低温度22.1 ℃。气体空间最高温度44.6 ℃，最低温度20.2 ℃。此时汽油饱和蒸气压为80.2 kPa。（6）十一月测得的大气平均最高温度15.6 ℃，平均最低温度7.8 ℃。气体空间最高温度28.7 ℃，最低温度9.3 ℃。此时汽油饱和蒸气压为50.2 kPa。为了分析浓度分布的规律按照以上提供的基本数据进行数值模拟，结果如图3：

从a图中看到，油气靠近罐顶位置处出现“空腔”，此时油气浓度为0，是因为呼吸阀入口位置侧漩涡导致的油气积聚效应尚未表现出来，但随着封闭时间的延长，低压区会造成油气聚集，无新鲜空气的补给，很快就会将空腔填满，出现如图b的现象。

随着大气温度的升高与罐内蒸汽压逐渐增大，更多的油气分子进入气体空间，罐内同一高度上的油气浓度逐渐增大，d图浓度近似饱和达到最大值0.948 0，而a图浓度出现最低值0.259 5。浓度的极大值均出现在油面附近0.25 m以内的区域。浓度最高与最低值之间平均变化区间（25.61%～48.61%）。气体空间温差越大，浓度变化坡度越小。此规律在24 h以及一年之内都与日照辐射的强弱同步变化。

该现象的出现，主要考虑在气体空间垂直方向上，液体的分子质量一般远大于空气的分子质量， 且油气分子更趋于在液面附近聚集，加之空气的吸入再次导致罐顶混合气被稀释。另外空气湍流作用，使得油品蒸汽压与密度的变化，出现了空气的分界面，使得高浓度更加集中于空间底部位置。

浓度梯度的变化有一个明显的拐点，油面附近的高浓度层在罐体气体空间高度的1/2以下，很快降低到一定值，以上的各点浓度基本保持这一值不变。饱和浓度的约85.27%变化发生在拐点之下;其余的14.73%变化在拐点之上，故拐点之上浓度分布均匀，曲线趋于平滑。

该现象的出现，一方面主要考虑围绕着罐壁附近很薄的一层油气混合气气体，受到黏性的作用附着在罐壁附近产生一个边界层，当罐壁在太阳辐射的作用下温度升高时，气体边界层将上移，使得罐顶部温度较低的油气，自上而下的冲击油面位置，减缓了油气的蒸发速度，因此油面附近的浓度依然会维持较高值。另一方面， 油罐装满度较低时，空气流进罐后无法直接冲击至油面位置， 油面附近的高浓度将不受其影响，始终保持一个较高数值。当储罐装满度较高时， 气体空间高度有限，从吸气阀进入的冷空气产生的冲击搅拌充分， 油气分子分布较为分散，因此浓度变化速率不大。

图3中出口位置处日出后2 h最高体积浓度为54.40%，第4 h最高体积浓度为59.76%，第8 h最高体积浓度为65.39%，第12 h最高体积浓度为70.51%。这主要是由于，在日出前气体空间温度出現最低值，新吸入罐体内部的新鲜空气加速了油气的溢出，但温度的降低却抑制了这一速度，而呼气一般出现在日出前的2 h内，将此时刻记为起始时刻，此后的12 h内包含了一个完整的呼气与吸气过程，此时的浓度计量对工程是有意义的。

5  结 论

（1）大部分时间罐内气体都是不饱和的，浓度变化速率以拐点为界，拐点之上变化快，拐点之下变化慢，拐点一般位于整个气体空间的中间位置。主要是对流扩散与搅拌的综合作用结果。气体空间的温度差值直接影响着浓度变化梯度呈现反向变化。

（2）利用本文创建的程序与算法，所得的模拟浓度值与实测数据相吻合。改正了已有计算方法忽略液体分子扩散过程与存储时间、空间高度之间联系的问题。能够依据用户需求，在任意装满度下，结合存储物质的组成、外部气候条件变化对扩散通量的影响，通过程序设定存储时间以及气体空间的网格跨度，精确掌握罐体内部储液的状态，为储罐的管理维护提供了便捷方法。

（3）该计算方法适用于化工厂、油库、码头等场合的浓度计算，若可找出第二类特殊边界条件，可进一步提高测算精度。

参考文献：

[1]郭光臣，董文兰，张志廉.油库设计与管理[M].山东：石油大学出版社，1991.

[2]API Bull 2518. Evaporation loss from fixed2roof tanks[R].USA：API，1962.