基于达布变换的特征值通信性能研究

梁 猛,任 新

(西安邮电大学 电子工程学院,西安 710121)

0 引 言

信号在光纤传输过程中会受到衰减、色散和非线性效应等影响,最终限制了传输容量。非线性薛定谔方程(Nonlinear Schrodinger Equation,NLSE)描述了信号在光纤中传输的复包络特性。为了研究NLSE,1972年,Zakharov等人在一个空间维度上找到了一个Lax对,并建立了Lax对方程[1]；在此基础上,Yousefi等人在2014年提出了一种用于解决光纤通信中色散和非线性的方法,即非线性傅里叶变换(Nonlinear Fourier Transform,NFT)法[2-4],NFT也称为逆散射变换(Inverse Scattering Transform,IST),在IST理论体系中,与NLSE相关的狄拉克型方程的特征值是不变的,NFT理论用连续和离散的非线性傅里叶谱表示信号,并且可以通过光路复用产生高阶孤子的传输[5]；2015年,Zhen等人提出了基于NFT的非线性频分复用传输[6]；2017年,Tao等人提出了一种基于NFT的光通信替代译码的方法[7]。但国内外几乎没有关于特征值优化的研究。

本文介绍了NFT理论推导和变换过程,并通过仿真软件对特征值通信进行了验证,在此基础上对特征值的选取范围进行了优化,进一步在优化特征值算法中对修正系数有了新的设定,演示了不同情况下解调出的离散特征值。仿真结果证明,特征值通信能在传输2 000 km的距离内很好地恢复发送信号。

1 NFT理论基础

1.1 NFT理论

用于描述光信号在光纤中传播的标准归一化NLSE可表示为

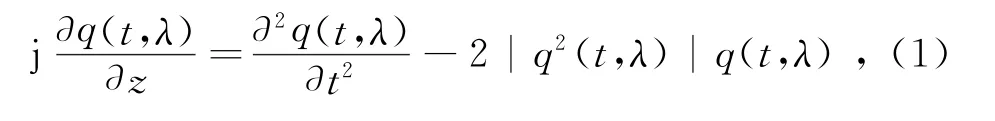
式中:j为虚数；q(t,λ)、t和z分别为信号、时间和距离的归一化系数；λ为NLSE的特征值。对NLSE进行NFT变换,可得到Zakharov-Shabat系统[2],即

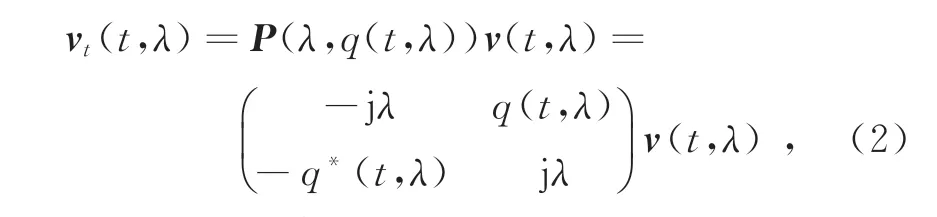
式中:q*(t,λ)为信号q(t,λ)关于特征值λ的共轭对称信号；P(λ,q(t,λ))为Lax运算符中的P算子[2]；v(t,λ)为特征向量,该特征向量为一个2×1的矩阵,令v(t,λ)=[v1(t,λ),v2(t,λ)]T,则v1(t,λ)和v2(t,λ)分别为v(t,λ)中的两个特征向量分量。

设v(t,λ)=[v1(t,λ),v2(t,λ)]T为式(2)在边界条件lti→m∞v(t,λ)=e-jλt下 的 一 组 解,令a(λ)=(t,λ)ejλt,b(λ)=(t,λ)e-jλt,其 中a(λ)和b(λ)称为非线性傅里叶系数,可得出信号q(t,λ)的NFT表达式为

式中:^q(λ)为 连 续 谱；~q(λk)为 离 散 谱；a'(λk)为a(λk)的导数；λk为信号q(t,λ)的第k个特征值；N为信号q(t,λ)包含特征值的个数。由式(3)可知,信号q(t,λ)的NFT由连续和离散谱两部分组成。

NFT有解析和数值法两种方法。解析法只能在矩形脉冲等少数波形中使用,具有一定的局限性,而数值法则适用于所有的波形。数值法通常使用Newton-Raphson搜索算法对特征值进行求解[3]。

以矩形脉冲和高斯脉冲为例。解析法只能求出矩形脉冲的连续和离散谱,而数值法可求出矩形脉冲和高斯脉冲非线性谱,文献[2]中求出了矩形脉冲为脉冲的幅度)分别在A=2和6时的NFT连续谱和离散特征值图像。

选取数值法中的The Ablowitz-Ladik Discretization法和Newton-Raphson搜索算法求高斯脉冲q(t,λ)=A e,式中:T为脉冲持续时间；T0为初始脉冲持续时间。图1所示为A=1和2时的NFT连续谱和离散特征值关系图,解析法则不能求出该函数的非线性谱。

图1 NFT连续谱和离散特征值关系图

1.2 达布变换

达布变换(Darboux Transformation,DT)能够以递归的方式构造多孤子信号。设q(t,λ1,λ2,…,λk)为多孤子信号,且φ(t,λk+1)=[φ1,φ2]T为式(2)的解,则可构造新的信号为

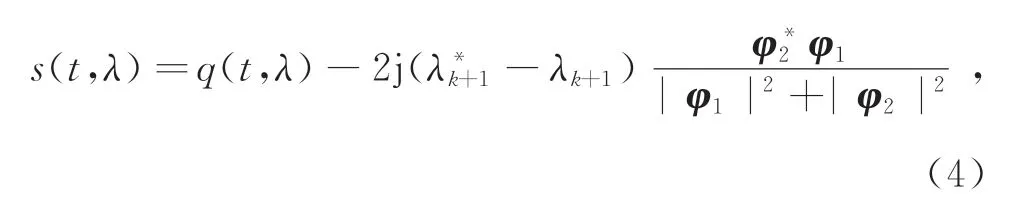
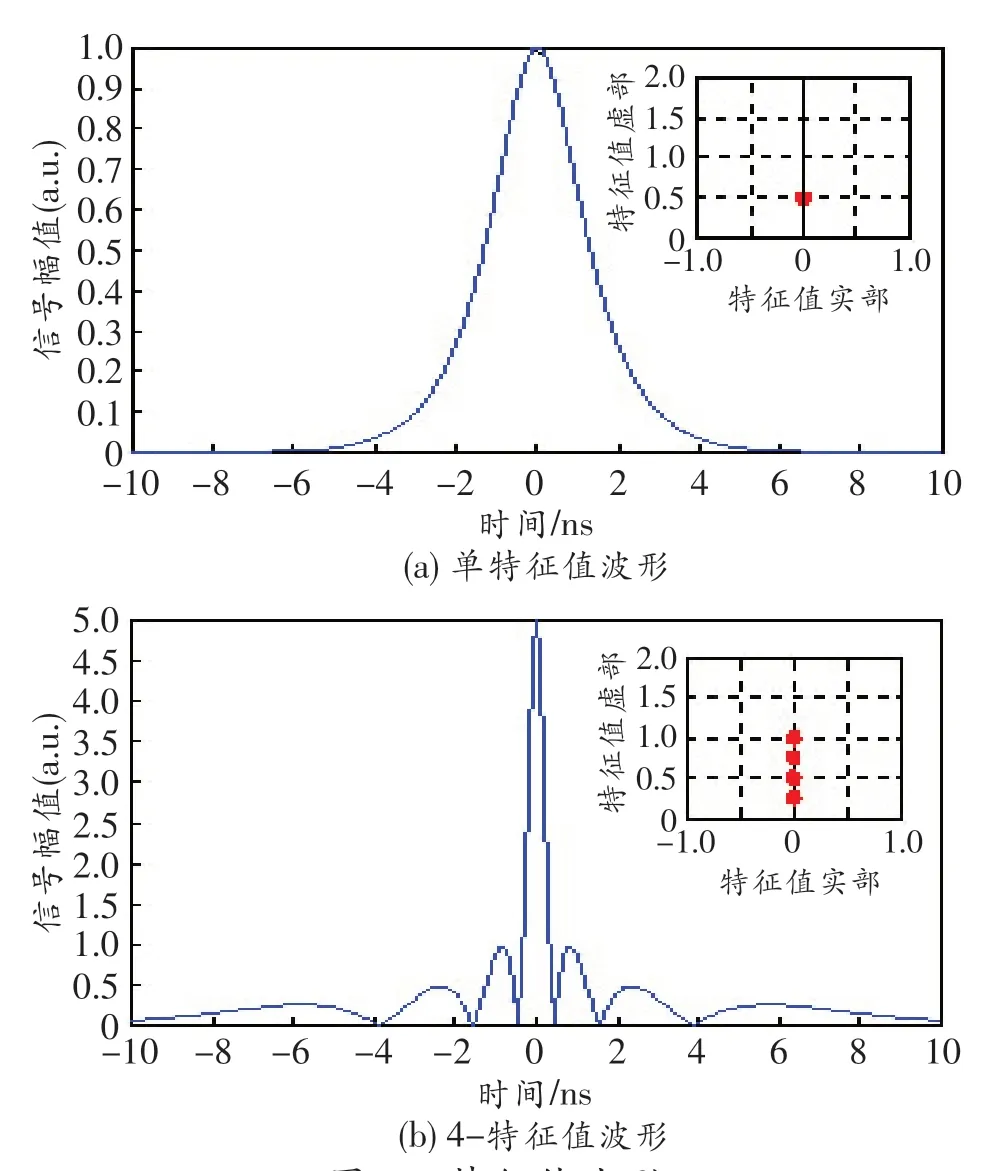
图2 特征值波形

2 系统模型

从理论上讲,光谱域中的4个自由度都可进行调制,即特征值的虚部产生归一化的振幅并调节脉宽；第2自由度是特征值的实部,调节频率偏移；第3和4自由度分别是离散谱的相位和振幅,它们分别改变了孤子的相位和位置。本文采用调制特征值虚部的方式来进行信号传输。系统框图如图3所示。

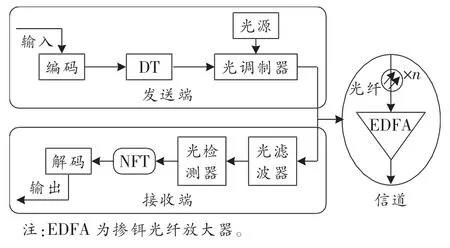
图3 实验系统框图

第1步,建立特征值与发送码元的对应关系。本文在验证过程中选取λ1和λ2两个特征值,发送端由纯虚数[8]特征值结合DT合成传输信号,用λ1合成的信号调制发送码元0,用λ2合成的信号调制发送码元1。信号通过光调制器产生适合在光纤中传输的光信号。

第2步,信道由n段光纤和EDFA构成,发送端传来的光信号经过一段距离的光纤后放大进入接收端。

第3步,接收端由光滤波器、光检测器和NFT模块构成,经信道传来的光信号经过滤波和检测后,由Newton-Raphson搜索算法解调出相应的特征值,从而解调出相应的传输码元[8]。

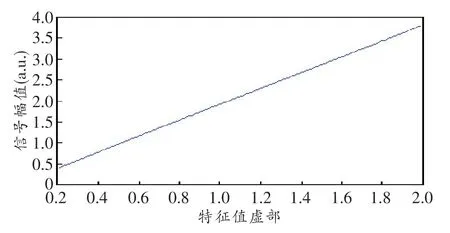
图4 幅度对特征值的影响

3 影响特征值的因素

3.1 脉冲幅度对特征值的影响

在无信道条件下,用Newton-Raphson搜索算法解调不同幅度的孤子波形,由图4可知,脉冲幅度变大时,解调出的特征值增大,近似为线性变化。当信号经过信道后,会受到色散和噪声的影响,为了更准确地解调特征值,应对幅度进行修正。修正过程为,首先对接收信号进行归一化处理,然后恢复原始幅度,进一步引入修正系数,最后得到的信号为

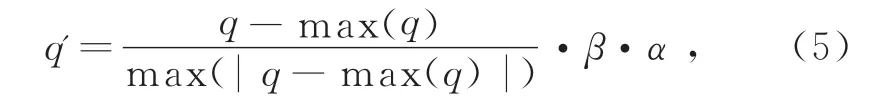
式中:q'为修正后的信号；β为信号归一化后理论上恢复原始幅度的系数；因实际中受到噪声的影响并不能很好地恢复原始幅度,所以引入α为信号q的修正系数,修正系数随着传输距离m的改变而改变。为了精确解调出特征值的大小,通过实验得到一系列α的具体值,表1给出了λ=0.2j、0.5j、0.8j和1.0j时在不同m下的α取值。

表1 α在不同m下的取值

在传输过程中,信号受到色散影响,接收到的波形会发生畸变,引起相位偏移,从而导致表1中的修正系数α随着传输距离m的增大而减小。

3.2 脉冲持续时间对特征值的影响

无信道条件下,用Newton-Raphson搜索算法解调不同脉冲持续时间的波形,得到的结果将有所差异。若脉冲持续时间选的不好,很有可能导致结果出错,图5仿真了采样点为256时不同特征值下的最佳脉冲时间,在此情况下,特征值能够被很好地恢复。若减小特征值对应的脉冲持续时间,会造成信息缺失。由图可知,脉冲持续时间对特征值的影响较为明显。

3.3 采样点数对特征值的影响

采样点数对特征值的影响在一定程度上变化较小,基本规律为采样点数越多效果越好。但考虑到硬件实现和减少计算复杂度,采样点数的选择应遵循以下规律:在几乎不影响解调的前提下,采样点数越少,计算复杂度越低,硬件越容易实现。图6所示为采样点数和误差之间的关系(误差指经过NFT解调后的特征值和原始特征值之间的差值)。由图可知,当采样点数为256时,误差控制在10-2以内,该采样点数可作为仿真实验的采样点数。

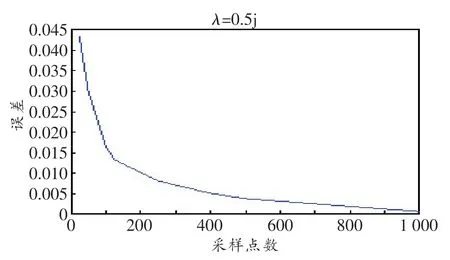
图6 采样点数和误差的关系图

总的来说,影响特征值的因素主要有脉冲的幅度、脉冲持续时间以及采样点数。相比于脉冲的幅度和脉冲持续时间,采样点数对特征值的影响相对较小。对于单孤子脉冲而言,特征值影响因素只能改变特征值大小,不改变特征值个数。图7所示为影响特征值的各因素变化与造成误差的关系图,为了确保采样点数几乎不影响整体解调性能,选取采样点数为1 000,由图可知,特征值不宜过大也不能太小,最佳选择在0.1j～j之间。

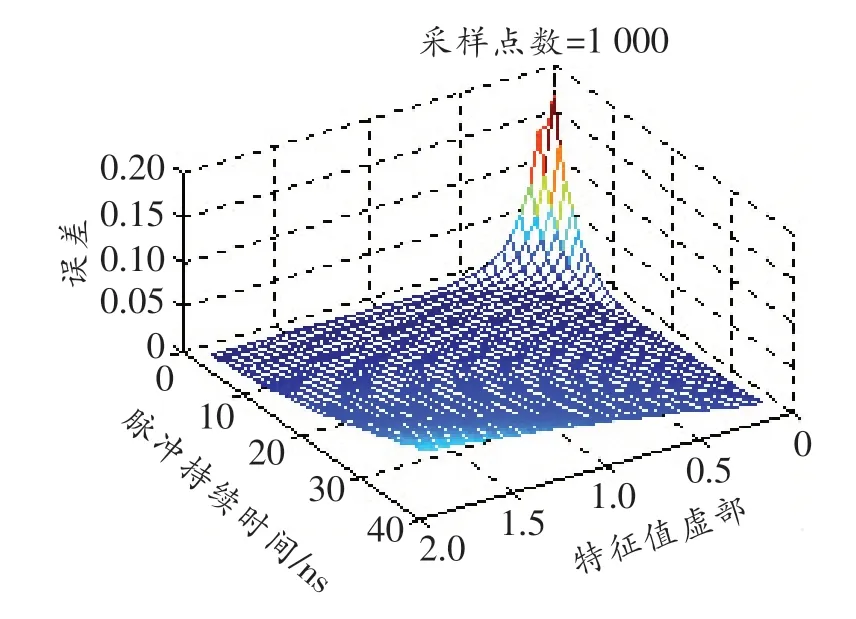
图7 误差图

在传统的特征值通信中,发送端用DT或非线性傅里叶逆变换(Inverse Nonlinear Fourier Transform,INFT)理论合成发送波形或在信道传输孤子波形,通过信道后,接收端用NFT理论求解特征值。但孤子波形对特征值的要求较高,不具有普遍性。而在特征值通信中,不同特征值组合通过信道后结果不同,传输距离受限。传统方法没有对特征值的影响因素作深入分析,也没有提出修正系数α的概念,引入α后不仅提高了传输距离,更能在很大程度上降低误码率。

在Matlab软件仿真系统中,采样点数越多,结果越精确,但硬件实现难度大。传统方法没有提到采样点数和特征值之间的关系,由图6和7可知,采样点数和误差的关系是减小硬件复杂度的主要依据。

4 实验仿真

4.1 仿真参数设置

实验采用图3所示的系统框图,采用Matlab和Optisystem软件进行仿真。参数设置为:入纤光功率为0；二阶色散系数β2=16 ps/nm/km；非线性系数γ=3×10-19m2/W；光纤线性衰减系数a=0.2 dB/km；噪声为高斯白噪声；采样点为256；传输速率为1 Gbit/s。传输链路中每段光纤长50 km,即信号每经过50 km光纤连接一个EDFA,放大器增益为10 d B,噪声为5 d B。

4.2 仿真结果分析

通过大量实验仿真发现,一般情况下解调的特征值不能恢复到初始特征值,传统的特征值通信在不引入修正系数α的条件下,传输距离有限,以λ1=0.5j、λ2=1.0j为例,由图8可知,传输距离为250 km时基本能解调出两个特征值。误码率为0.002、传输距离为1 000 km时,解调出的特征值出现了严重的混叠现象,误码率大概为0.25。由此可知,在特征值为λ1=0.5j、λ2=1.0j的情况下,800 km基本为此时的极限距离。图9所示为入纤光功率为0 dBm的条件下,1 000 km内不同距离下的误码率。由图可知,800～900 km后误码率增加至10-1量级。

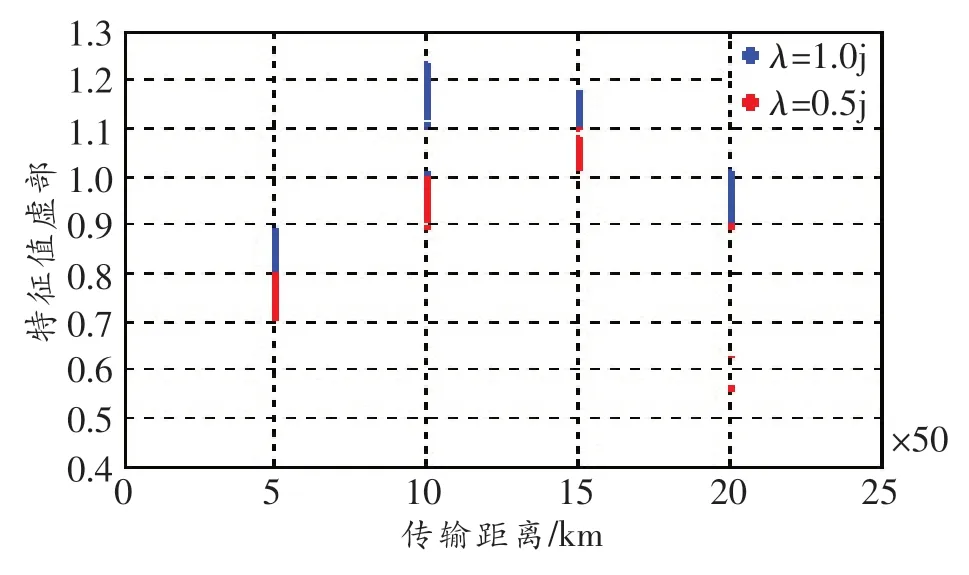
图8 特征值随传输距离的变化

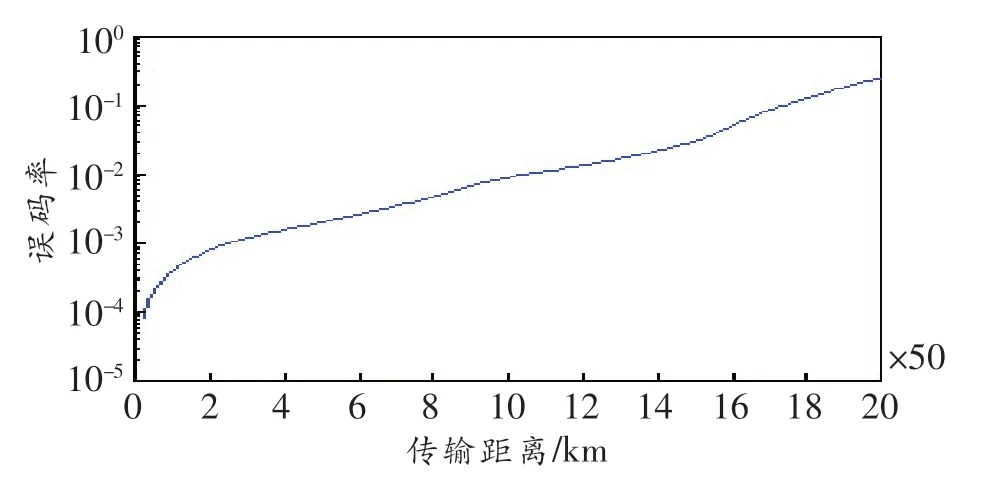
图9 0 dBm入射光功率时误码率随传输距离的变化

但引入修正系数α后,能很好地区分开两个不同的特征值。在解调特征值的算法中,信号q的修正系数α随着特征值的大小和传输距离的改变而改变。将表1中的α取值代入系统可清晰地区分出λ1=0.2j、λ2=0.8j和λ1=0.5j、λ2=1.0j两种情况下,1 kbit信息在2 000 km距离传输的特征值变化情况。图10仿真了两种特征值取值随传输距离的变化情况。可以看出,α在表1下的取值能够很好地区分开两个特征值,且传输距离在2 000 km以内时误码率为0。由于受到噪声和色散的影响,在传输过程中,随着传输距离的增大,两个特征值越来越接近,不同的特征值传输的极限距离会有所不同。但可确定的是,选取合适的特征值,传输距离都可达到2 000 km以上。

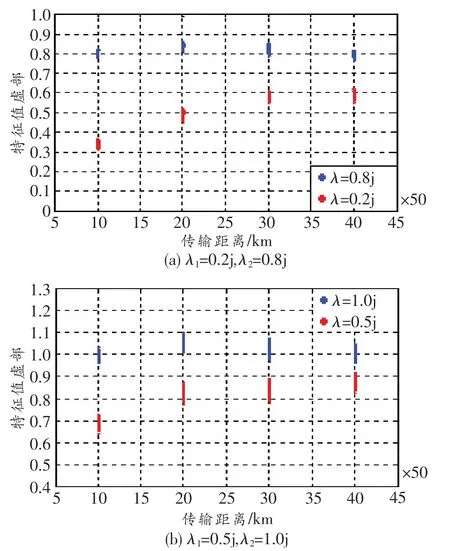
图10 特征值随传输距离的变化

由两种对比可知,在传输系统相同条件下,改进后的特征值通信具有传输距离更远和误码率更小的优势。随着入射光功率的增大,特征值偏差逐渐增大,误码率逐渐增大。以λ1=0.5j、λ2=1.0j为例,图11所示为不同传输距离下入射光功率与误码率的关系。由图可知,在误码率为10-3量级下,传输距离为500 km时,入射光功率可以增大到12 dBm；传输距离为2 000 km时,入射光功率只能增大到5 d Bm。即在保证通信质量的前提下,光功率增大,非线性效应增强,传输距离减小。

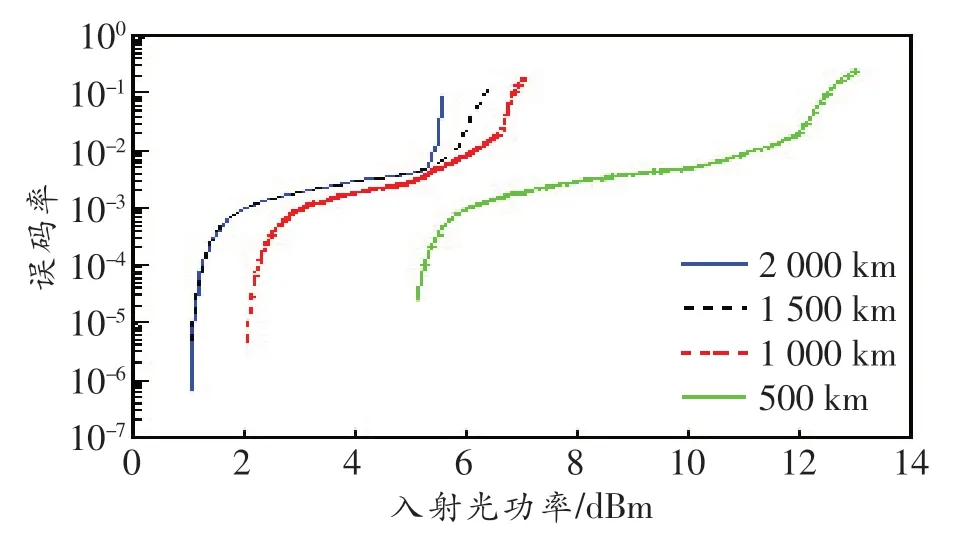
图11 入射光功率与误码率的关系

4.3 特征值取值范围优化

理论上讲,特征值可取任何虚数。但由于不同特征值对应的孤子波形幅度和持续时间都不同,在该仿真条件下,受到马赫-曾德尔调制器(Mach-Zehnder Modulator,MZM)对幅度的限制,特征值取值趋向于一个范围。在长距离传输过程中,由于噪声和能量转移的影响,随着传输距离增大,两个特征值越来越靠近。图12所示为发送1 kbit的信息传输2 000 km,取λ1=0.2j和λ2=x·j(x=0.3,0.4,0.5,…,1.3)时两个特征值大小之差。λ=0.1j时,需要的采样点数较多,为了降低复杂度,取采样点数为256,忽略λ=0.1j的取值,所以从λ=0.2j开始取值,x以0.1为间隔依次取值。由图可知,从λ=0.4j开始,到λ=1.2j之前,信息都可传输2 000 km的距离且能区分出原始特征值。取λ1=0.2j、λ2=1.3j及其以后的取值时,λ2合成的波形过于集中在一个小范围内,且幅度过大,受到MZM和采样点数的影响,采样后的波形失真严重,无法体现出原始波形的信息,所以传输2 000 km后解调出的两个特征值产生混叠。因此在图3的实验系统框架下,特征值取值范围应固定在λ=0.2j到λ=1.2j之间,且原始特征值之差应≥0.2j。

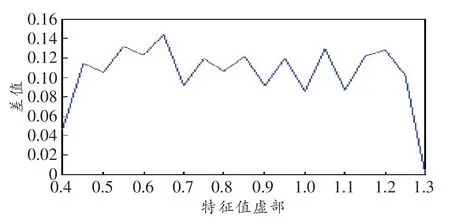
图12 λ=0.2j与其他特征值在传输2 000 km距离后的差值

5 结束语

本文根据NFT理论和DT对特征值进行调制解调。考虑了脉冲幅度、脉冲持续时间和采样点数3个影响因素后,选取两个不同的特征值。在发送端利用DT生成两种孤子脉冲,承载信息后一次发送1 kbit的信号,通过OptiSystem软件仿真系统,在接收端归一化处理,训练出修正系数,然后使用搜索算法得到信号NFT的数值解,并从中提取出特征值从而恢复原始信号。进一步通过仿真实验得出了特征值的取值范围,加强了系统的可实现性。

本文仅在特征值取纯虚数的情况下对单特征值进行了优化,下一步工作中可以对多特征值通信进行研究,以达到更高的传输速率。