内容分块数据中心光网络灾前数据转移

揭水平,李泳成

(1.苏州大学 电子信息学院,江苏 苏州 215006; 2.中天宽带技术有限公司,江苏 南通 226000)

0 引 言

数据中心光网络中每个数据中心都存储了用户大量的重要数据,一旦受到自然或人为灾难(例如地震、台风和战争等)影响,将造成重要数据的永久丢失。为避免这种情况发生,数据中心光网络通常采用高效的内容备份策略,如内容复制(Content Replication,CR)[1]和内容分块(Content Fragmentation,CF)[2]。高效的内容备份策略能确保单个数据中心发生故障后数据中心光网络中存储的数据被恢复[3]。然而,发生大范围灾难时,多个数据中心同时毁坏,内容备份无法保证所有内容都被恢复,必须转移灾难区域内存储的部分数据[4]。由于数据中心中存储了海量数据,其需要转移的数据量为TB级甚至PB级。因此,如何对多个数据中心的大量数据在短时间内进行快速数据转移是一个具有挑战性的问题。Ferdousi等人虽然针对CR数据中心光网络提出了一种数据转移算法[5],但目前并没有针对更为复杂的CF数据中心光网络数据快速转移问题的相关研究。

本文对CF数据中心光网络灾前数据转移问题展开研究,首次针对该问题进行了问题描述,构建了混合整数线性规划(Mixed Integer Linear Programming,MILP)模型且为大规模网络也提出了一种高效的最小时延(Least Delay,LD)快速数据转移算法(简称LD算法)。仿真结果表明,LD算法性能与MILP模型接近,证明了其高效性。其次,本文也首次从灾前数据转移性能的角度评估了CF与CR策略的性能差异。仿真结果表明,相同数据冗余度情况下(都为100%),采用LD算法的CF数据中心光网络比CR数据中心光网络最多节省42%的数据转移时间。

1 CF数据中心光网络灾前数据转移问题

CR策略是复制出x个备份,然后将所有的x+1份相同内容存储在不同的数据中心。该策略的优点是只有当所有x+1份内容都被灾难损毁时内容才会丢失；缺点是数据冗余度非常高(≥100%),严重降低了存储资源的利用率。为降低数据冗余度,一种拥有更高存储资源利用率的CF策略被提出。该策略使用(k,r)擦除编码,首先将一个大小为F GB的内容平均拆分为k个内容块,每个内容块的大小为F/k GB；然后,再额外添加r(r＜k)个大小为F/k GB的奇偶校验块,最终形成k+r个数据块。CF策略允许在k+r个数据块中≤r个数据块丢失的情况下,整个内容仍可被恢复,因此其数据冗余度为r/k＜100%。本文中的CF策略采用了具有较小编码开销的Reed-Solomon(RS)擦除编码[6]。大范围灾难发生前,一旦某个内容中有ψ(ψ＞r)个数据块在灾难区域中,为保证内容不丢失,则需将ψ-r个数据块从受灾区域转移到安全的数据中心中存储。

1.1 CF数据中心光网络灾前数据转移实例

图1所示为一个CF数据中心光网络灾前数据转移实例。假设该CF策略采用RS(5,2)编码将内容分成了5个内容块和2个奇偶校验块共7个数据块(即k=5,r=2),并将其存储在各个节点(N2、N3、N4和N5)的数据中心中。具体的,节点N2、N3和N5都存储了2个数据块,节点N4存储了1个数据块。假设M区域即将发生大范围灾难,节点N2和N3将被损毁。这两个数据中心存储的ψ=4个数据块即将丢失。因此,最少需要转移ψ-r=2个数据块。现有两种数据转移方案S1和S2。方案S1将数据块4沿路径N2-N1-N5转移至数据中心N5,转移时间为3 s；将数据块6沿路径N2-N1-N4转移至数据中心N4。由于共享链路N2-N1,数据块6需要等到数据块4转移完成后再进行转移。因此,方案S1所需的转移时间为6 s。方案S2则将数据块4沿路径N2-N1-N5转移至N5,数据块7沿路径N3-N4转移至数据中心N4,总转移时间为4 s。方案S2比S1节省了33%的转移时间。

图1 CF数据中心光网络灾前数据转移实例

1.2 问题描述

给定一个数据中心光网络G(N,L,D,C)。其中,N为节点的集合；L为链路的集合；D为数据中心的集合；C为存储内容的集合；αc为内容c的重要性权重。假设一个大范围灾难即将影响区域M,Din为M内数据中心集合,Do为M外数据中心集合。CF数据中心光网络灾前数据转移问题的目标是在恢复所有内容的前提下,最小化数据转移时间。

本文考虑多个约束条件,包括:(1)通过转移,所有内容都被恢复；(2)每一个数据块有且只有一条转移路径；(3)重要性权重高的内容先完成转移；(4)数据中心光网络中每条链路上带宽资源有限；(5)任意两个数据块转移路径重叠时,其转移时间不重叠；(6)每个数据中心存储资源有限；(7)节点之间采用链路不相交的k-shortest算法搜索k条最短路由。

2 MILP模型

基于上节的问题描述,我们构建了一个MILP模型,其集合、参数、变量和优化目标定义如下。

集合:

G(N,L,D,C) 网络拓扑。

Pd,sd、s两节点间k条最短路径的集合,d,s∈D:d≠s。

DinM内数据中心集合。

DoM外数据中心集合。

Gc内容c在M内存储的数据块集合。

Pd节点d到安全数据中心路径集合∪s∈DoPd,s。

参数:

αc整数,内容c的重要性权重值。

Bp整数,路径p的可用传输容量。

N 内容c数据块总数。

r 内容c需转移数据块总数。c

Sd/Gb yte 数据中心d可用存储资源。

Δ 一个极大值。

变量:

T 整个网络数据转移时间。

优化目标:最小化T。

约束条件:

内容c转移数据块总数达到恢复要求。

内容c第k个数据块沿路径p转移的传输时间。

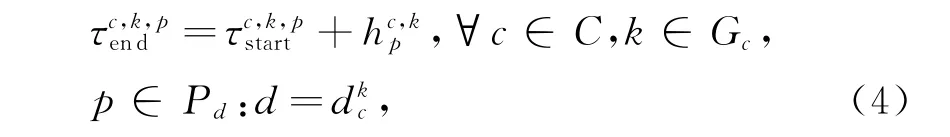
内容c第k个数据块沿路径p转移的结束时间。

计算内容c转移的开始时间,该时间不大于内容c任意一个数据块转移的开始时间。

计算内容c转移的结束时间,该时间不小于内容c任意一个数据块转移的结束时间。

内容c数据块转移路径共享链路时,确保这些数据块转移时间不重叠。

重要性高的内容优先转移。

重要性相同的内容,内容数据块使用相同链路转移时,确保内容转移时间不重叠。

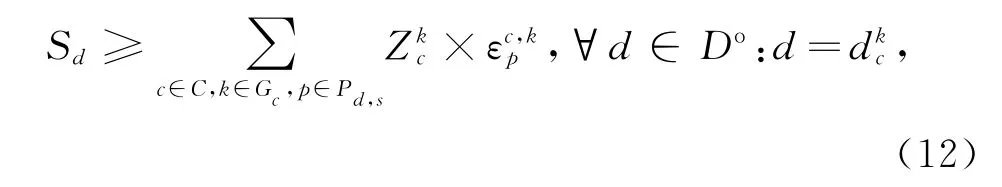
数据中心存储的数据不能超过其存储资源限制。

计算整个网络的数据转移时间。

整个网络的数据转移时间大于所有内容的传输时间之和(冗余公式加快模型求解速度)。

3 LD算法

虽然MILP模型能找到问题的最优解,但受限于其高计算复杂度,无法为大规模网络在有限时间内获得最优解。目前,并没有专门针对CF数据中心光网络数据转移的算法。由于既要选择转移的数据块,又要选择转移路径,整个问题变得更加复杂。本文为CF数据中心光网络提出一种LD算法,该算法主要分为两部分,转移内容的选择和转移数据块及转移路径的选择。

3.1 转移内容的选择

遍历各个数据中心存储的所有内容,一旦某个内容在灾难区域内存储的内容块总数超过r,则将其加入到转移内容集合CEva。遍历完所有内容后,将集合CEva中的内容按照其重要性权重值αc由大到小排列。

3.2 转移数据块与转移路径的选择

针对获取的集合CEva,该启发式算法将进一步为每个内容选择转移的数据块及每个转移数据块的转移路径。具体步骤如下:

End for

对于内容c,遍历其在灾难区域内存储的数据块集合Gc,对其中每一个数据块分别计算所有可能转移路径的转移时间,并计算LD(即每个数据块结束转移的时间)。比较每一个数据块的LD,选择具有最小LD的数据块k*进行转移。从Gc中移除已转移的数据块k*,若转移的数据不足以恢复内容c,则重复以上步骤,否则选择下一个内容进行转移。当所有内容完成转移时,获取整个网络数据转移时间T。

图2 测试网络拓扑图

4 结果与性能分析

4.1 测试条件

为评估所提算法的性能,我们考虑了如图2所示的两个测试网络,图2(a)为具有6个节点、8条链路和6个数据中心的n6s8网络,图2(b)为具有24个节点、43条链路和8个数据中心的USNET网络。假设一个大范围灾难将分别影响n6s8网络中的节点1和2以及USNET网络中的节点6、9和12。每个数据中心可用存储资源在10～100 TB范围内均匀分布,且平均占用率为40%(剩余60%可用于存储转移内容块)。网络中每个链路上的传输容量在500 Gbit/s～1 Tbit/s范围内,其中30%用于传输数据中心间正常的业务(剩余70%可以用于数据转移)。假设数据中心存储的每个内容的大小在200～500 GB范围内均匀分布。这里的单个内容都是由许多较小的内容聚合而成。每个内容的重要性因子从1～10分成10个等级,因子越大,重要性越高。在MILP模型中,我们采用了K条最短路径搜索算法为每个节点对找到了3条最短路径作为候选路径。通过商用软件AMPL/Gurobi[7](版本5.6.2)求解MILP模型,模型的MIPGAP(Relative MIP Optimality Gap)设置为1%。启发式算法使用JAVA进行仿真。

4.2 整个网络数据转移时间

图3比较了MILP模型与LD算法的整个网络数据转移时间。其中,数据中心光网络采用基于RS(4,2)编码的CF策略进行内容备份。

图3 整个网络数据转移时间

由图可知,在两个测试网例的结果中,MILP模型所需的整个网络数据转移时间较短,LD算法的结果与MILP模型结果总是非常接近。其次,随着整个网络存储内容总数的增加,MILP模型和LD算法所需的整个网络数据转移时间越来越大。这是因为整个网络存储内容总数的增加将导致需要进行数据转移的内容增加,从而增加了整个网络数据转移的时间。最后,在USNET网络中,MILP模型和LD算法所需的整个网络数据转移时间都少于n6s8网络。这是因为USNET网络的平均节点维度高于n6s8网络,能为转移的数据提供更多的可选路径。

4.3 CF vs CR

本文也比较了CF和CR策略在转移内容数据总量和数据转移时间方面的性能差异。图4给出了在USNET网络中,两种策略需要转移的内容数据总量。图中每个点为基于6个随机种子仿真结果的平均值。CF分别采用了RS(2,2)、RS(3,2)和RS(4,2)3种编码方式,数据冗余度分别为100%、67%和50%。CR为每个内容都复制了一个备份(即x=1),数据冗余度为100%。

由图可知,随着整个网络存储内容总数的增加,两种策略需要转移的内容数据总量也不断增加。这也是由于整个网络存储内容总数的增加将导致需要进行数据转移的内容增加。我们发现,当k值增大时(即数据冗余度降低),其需转移的内容数据总量也将变大。这是因为更低的数据冗余度使得内容无法恢复的概率更大,需要进行数据转移的内容变得更多。在相同数据冗余度下(都为100%),CF所需转移的数据与CR相比最多节省了34%。

图5所示为两种内容备份策略的整个网络数据转移时间。CF采用了LD算法,CR采用了文献[5]中的算法。由图可知,当数据冗余度都为100%时,CF数据中心光网络比CR数据中心光网络最多节省42%的数据转移时间；当数据冗余度为67%时,CF数据中心光网络依然可以比100%数据冗余度的CR数据中心光网络更快完成数据转移；当数据冗余度为50%时,CF数据中心光网络与CR数据中心光网络相比,无法总是获得更低的数据转移时间,这与其需要转移的数据总量过大有关。

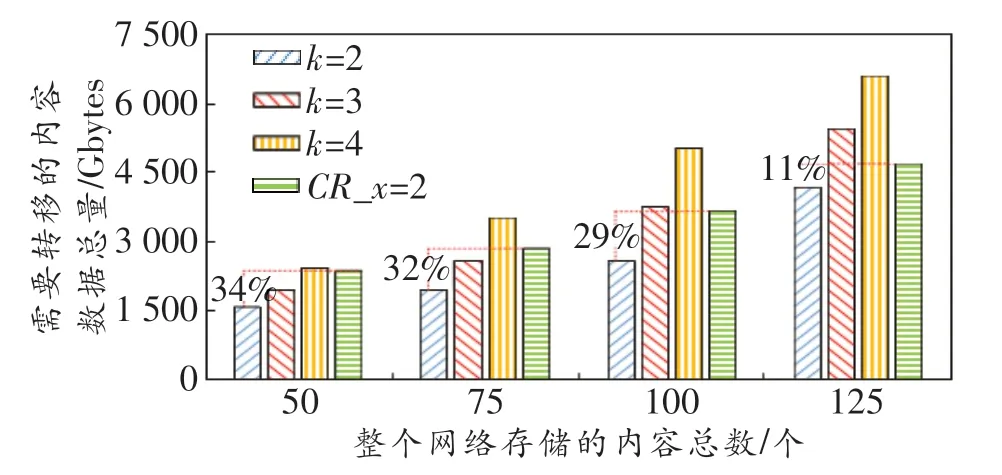
图4 CF和CR策略中需要转移的内容数据总量

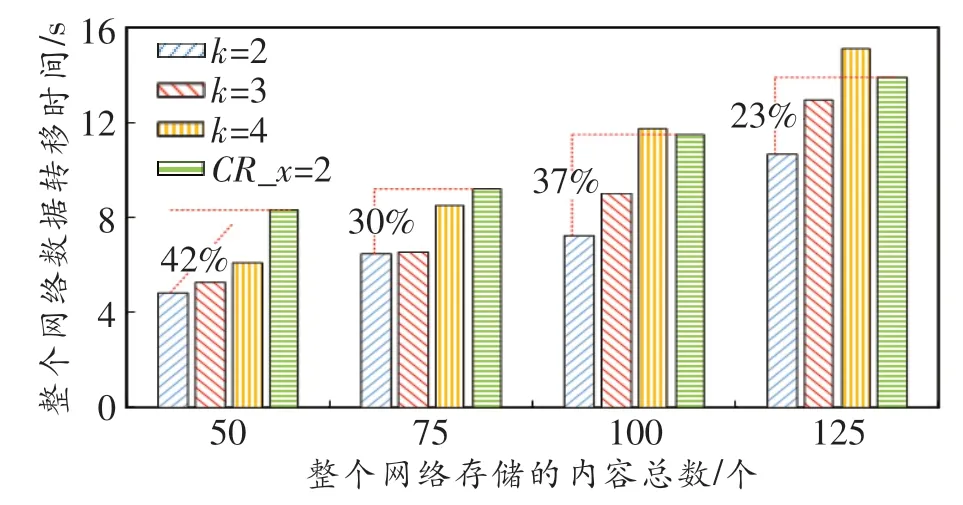
图5 CF和CR策略中整个网络数据转移时间

5 结束语

本文针对CF数据中心光网络灾前数据转移问题展开了研究。以最小化整个网络数据转移时间为目标,构建了一个MILP模型并提出了一种LD算法。仿真结果表明,LD算法与MILP模型的最优解非常接近。同时,我们也比较了CF和CR策略在灾前数据转移方面的性能。结果表明,数据冗余度都为100%时,采用LD算法的CF数据中心光网络比CR数据中心光网络最多节省42%的数据转移时间。