基于ADINA的地下水库抽水效应数值模拟

周清丽

(新疆水利水电勘测设计研究院，新疆 乌鲁木齐 830000)

在干旱半干旱地区，地表水资源普遍匮乏且极不可靠，地下水是这些地区的主要水源[1-2]。然而，这些地区的地下水主要是化石水，不能满足人类和生态系统的需要。因此，需要采取一些人为措施对含水层进标可持续管理。地下水水库建设对提高水资源利用水平，保障供水安全具有重要作用[3-4]。地下水水库是我国目前比较流行的一种水资源管理方法，类似于美国的蓄水与恢复的概念。与地表水水库相比。地下水水库具有占地少、不迁移、蒸发少、结构简单等优点[5-7]。目前，地下水库主要有三种利用方式，主要是地表水和地下水的联合利用，以增加地下水资源；恢复地下水过度开采形成的助陷锥；减轻沿海地区地面沉降、水土流失、海水入侵等典型地质灾害[8-9]。为了解决水资源调蓄问题，渗透系统的分流是关键施工技术之一[10-11]。

本文以某地下水库的抽水设施为例，建立模型。借助有限元软件ADINA模拟了地下水库抽水对沉降的影响，分别模拟了不同流量的单井抽水对沉降的影响，不同抽水井数(单井、双井、三井)抽水对沉降的影响[12-13]。

1 工程概况

地下水库场地位于古河道沉积区，地基土属于第四纪上更新世Q3至全新世Q4沉积物，主要由粉性土、饱和黏性土和砂性土组成。按其成因类型、沉积年代及物理力学性质的差异，可划分为 8 个主要土层。

本场地无地表水存在，地下水分为上部潜水、下部微承压水和承压水。

(1)潜水。该地区浅部土层中的潜水，年平均地下水位离地面0.5～0.7 m，埋深一般离地面0.3～1.5 m。由于潜水与大气降雨密切相关，所以水位呈现季节性波动，因此潜水水位的高低主要取决于降雨持续时间和降雨量的大小。

勘察报告提供的勘察期间地下水水位埋深约为0.80～2.10 m，相应绝对高程为2.12～3.70 m。

(2)微承压水和承压水。经过勘察可知，拟建场地内浅部分布有砂质粉土、夹粉质黏土，该土层的地下水水量比较丰富，并且具有一定的承压性，属于微承压水含水层。其深部分布有粉细砂层，该土层赋含地下水丰富，是承压含水层。

根据区域性水文地质资料，微承压水及承压水水位埋深一般约为地面以下3～11 m，随季节呈周期性变化。本实例采用体建模方式建立几何模型，模型长取100 m，宽取60 m。模型总共有8层土，3个抽水井，对其标号分别为1、2、3，井点间距为15 m。8层土接触面之间采用面链接。模型选用的是摩尔-库伦模型。这8层土的单元组类型都选为3D Soilid，将第4、6、8层土的Element Option设置为Porous Media，即：对第4、6、8层土考虑水土耦合时的孔隙压力作用。在多孔介质属性中定义这三层土分别在X、Y、Z方向的渗透系数。

本文主要研究不同井数(单井、双井、三井)抽水及不同抽水流量对沉降的影响。抽水流量Q分别取100 m3/d，300 m3/d，600 m3/d，利用公式计算孔隙流速，对应的流速分别为1.88 m/d，5.64 m/d，11.29 m/d。

单井抽水时，在3号井的第4、6、8层土各面上施加抽水荷载，双井抽水时，分别在2号井和3号井的第4、6、8层土各面上施加抽水荷载，三井同时抽水时，分别在1号、2号、3号井第4、6、8层土各面上施加抽水荷载。

本实例共划分为98 402个单元。第1层土划分为7047个单元，第2层土划分为7602个单元，第3层土划分为6742个单元，第4层土划分为5652个单元，第5层土划分为7894个单元，第6层 土划分为9316个单元，第7层土划分为8304个单元，第8层土划分为45 845个单元。

2 研究方法

2.1 有限元计算模型

本模型模拟单井抽水、双井同时抽水和三井同时抽水三种抽水方式对地面沉降的影响。三种方式的模型相同，只是施加的抽水荷载不同。其模型网格及荷载如图1所示。

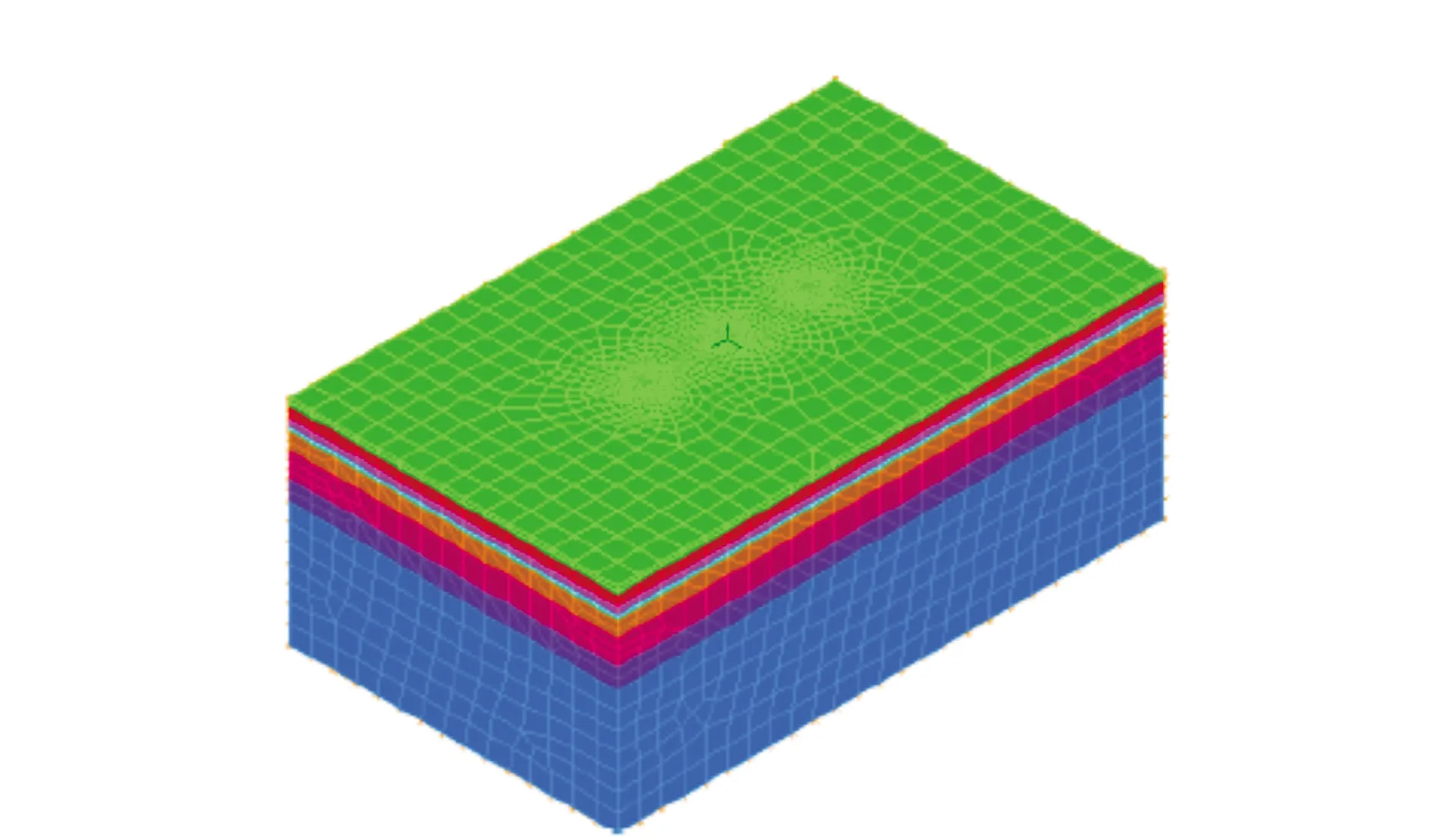
图1 有限元模型

2.2 选取观测点及节点

模型中三个井的标号分别为1号、2号、3号，选取两个点作为观测点。1号井在中间，选1号井中心点为一个观测点，2号、3号井距1号井的距离相同，选其中一个井点中心作为观测点即可，本文选3号井中心点作为观测点。

地面竖直方向沉降路径曲线图，是绘制距井点距离由近到远变化时，竖直方向的沉降量变化情况，在绘制地面竖直方向沉降路径曲线图时，需要确定距井点的距离，故要在模型中选择单元节点。每个土层选择两条路径，一条是距井点1的中心点由近到远的路径，称为路径1，一条是距井点3的中心点由近到远的路径，称为路径3。本章模型对第4、6、8土层施加抽水荷载，故在绘制地面竖直方向沉降路径曲线图时，选择第1、4、6、8层四个土层进行绘制，选取的结点为这四层土路径1和路径3上的结点。选取的两条路径如图2所示，两条黑线分别表示选取的两条路径。

图2 路径曲线

因为模型每个土层划分的单位不同，选取的节点不在路径1和路径3这两条直线上，而是在这两条路径附近，所以每个土层和每条路径选取的节点个数有所不同。

3 结果与分析

3.1 不同井数抽水及不同抽水流量对沉降的影响

通过模拟了单井抽水，双井抽水和三井同时抽水三种工况下对沉降的影响，单井抽水时，将荷载施加在3号井上，双井抽水时，荷载施加在2号井和3号井上。同时，还模拟了三种工况下不同抽水流量对沉降的影响，抽水流量分别为100 m3/d，300 m3/d，600 m3/d。得出各种工况下的竖直方向沉降量情况见表1。

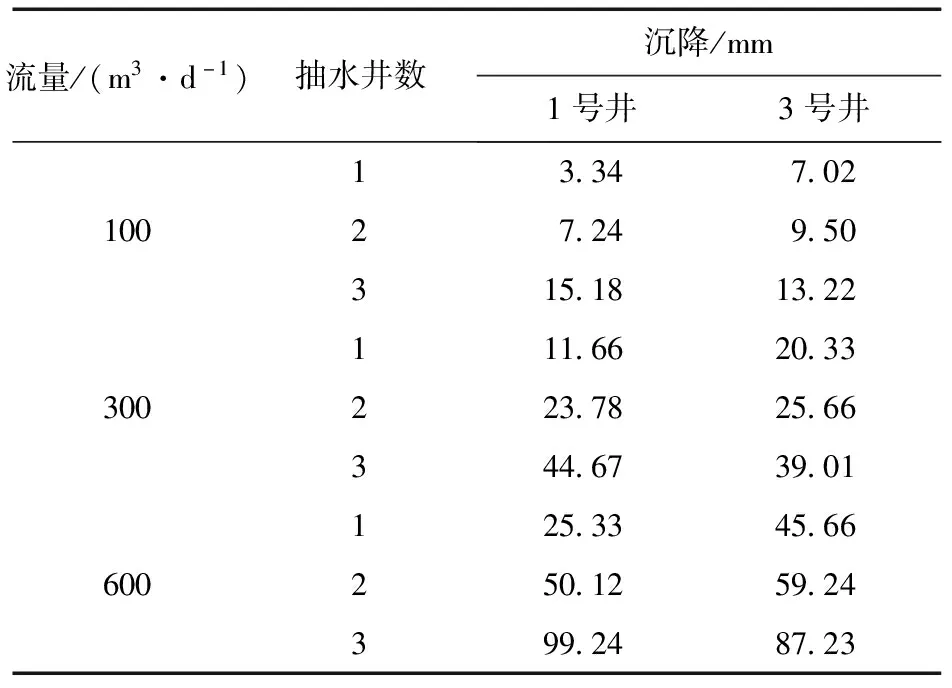
表1 沉降量对比表

由表1中数据可以看出:

(1)在抽水流量一定时，单井降水沉降较小，随着降水井点的增多，沉降逐渐增大。单井降水时，井点附近沉降最大，随着距井点距离的增大，沉降逐渐减小。

(2)在抽水流量一定，2号、3号井同时降水时，最大沉降发生在2号、3号井附近，1号井也产生沉降，沉降量比2号、3号井小。

(3)在抽水流量一定，1号、2号、3号井同时降水时，2号、3号井降水对1号井产生影响，使最大沉降发生在1号井附近，其次是2、3号井附近。随着降水井点的增多，1号、2号、3号井附近沉降都逐渐增大，1号井附近沉降增长最快。

(4)随着抽水流量的增大，沉降逐渐增大，三井同时降水时沉降增长最快，双井降水沉降增长速度次之，单井降水沉降增长最慢。

3.2 不同井数抽水及不同抽水流量对孔隙水压力的影响

通过分析单井抽水，双井抽水和三井同时抽水三种工况下降水对孔隙水压力的影响，以及三种工况下不同抽水流量对沉降的影响，抽水流量分别为100 m3/d，300 m3/d，600 m3/d。计算得到孔隙水压力云图的切片图，其中，孔隙水压力云图的切片图有两个查看结果，一个是1号井中心点的切片查看结果，称为观测点1的切片查看结果，一个是3号井中心点的切片查看结果，称为观测点3的切片查看结果。得出不同井数抽水、不同抽水流量抽水对孔隙水压力的影响规律，以及不同部位孔隙水压力的变化规律。将不同工况，不同部位孔隙水压力的数值列于表2中。

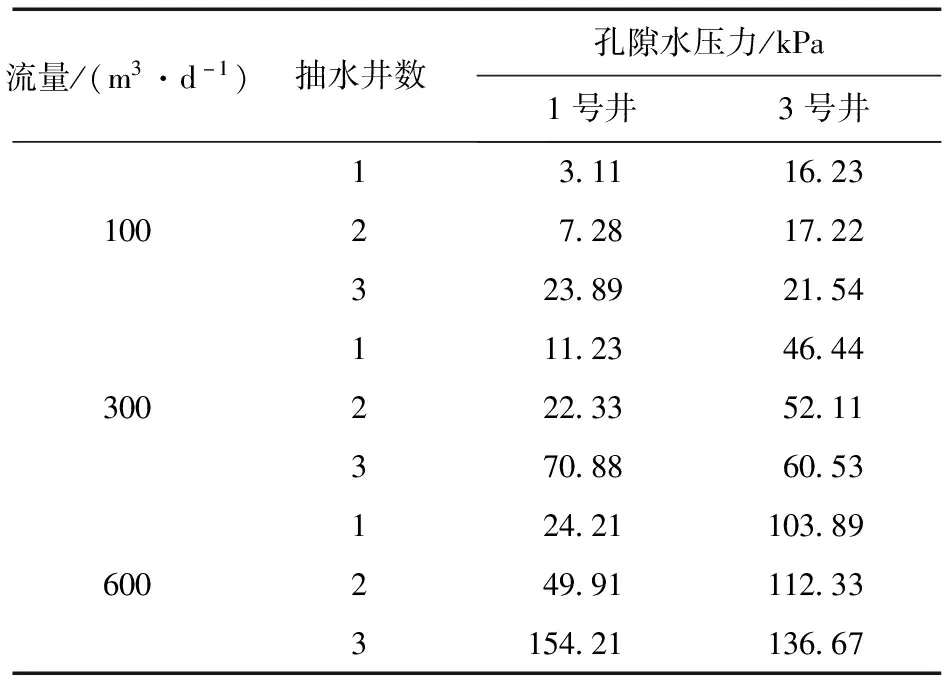
表2 孔隙水压力对比表

由表2中的数据可以看出:

(1)在抽水流量一定，单井抽水时，井点附近孔隙水压力最大，随着距井点距离的增大，孔隙压力逐渐减小，每个土层的孔隙水压力都呈现漏斗状。第4层和第6层土的孔隙水压力比第八层的大，延伸的范围更广。

(2)在抽水流量一定，2号、3号井同时降水时，每个井的孔隙水压力都增大，2号、3号井附近孔隙水压力比1号井附近的大，1号、2号、3号井同时降水时，1号井附近孔隙水压力最大，2号、3号井附近孔隙水压力大小次之。

(3)随着抽水流量的增大，孔隙水压力逐渐增大，三井同时降水时孔隙水压力增长最快，双井降水孔隙水压力增长速度次之，单井降水孔隙水压力增长最慢。

对于竖直方向上的沉降路径分析可知，随着距井点距离的增大，竖直方向沉降量逐渐减小。并且距井点较近时，第八层沉降量最小，下来依次是第一层、第四层，第六层沉降量最大，当距井点达到一定距离时出现转折点，第八层沉降量依然最小，第六层次之，第一层沉降量最大。在抽水流量一定时，单井抽水工况下沉降量最小，随着抽水井数的增加，沉降量逐渐增大；抽水流量较小时，转折点的位置随着抽水井数的增多向距离井点越远处移动，且移动距离较大，抽水流量较大时，出现转折点的位置基本不变。随着抽水流量的增大，竖直方向沉降量逐渐增大。单、双井抽水时，路径3的沉降量比路径1的沉降量大，双井抽水时，路径1的沉降量比路径3的沉降量大。

4 结 论

本文主要研究了不同井数(单井、双井、三井)抽水对沉降的影响，得出以下结论：

(1)随着距井点距离的增大，竖直方向沉降量逐渐减小；随着抽水井点数的增多，沉降逐渐增大；随着抽水流量的增大，竖直方向沉降量逐渐增大。

(2)距井点较近时，第八层沉降量始终最小，下来依次是第一层、第四层，第六层沉降量最大，当距井点达到一定距离时出现转折点，第一层沉降量最大，第四层次之。

(3)井点附近孔隙水压力最大，随着距井点距离的增大，孔隙水压力逐渐减小，每个土层的孔隙水压力都呈现漏斗状。第四层和第六层土的孔隙水压力比第八层的大，延伸的范围更广。