饱和时滞非线性系统的间接线性矩阵不等式抗饱和设计

李豪杰,何汉林,查 苗

(海军工程大学基础部,湖北武汉 430032)

1 引言

执行器饱和又称输入饱和,存在于几乎所有的现实控制系统中,对于时滞非线性系统来说也是如此.因此,研究饱和时滞非线性系统的抗饱和设计是非常有意义的[1].解决这个问题有3个难点:一是非线性系统;二是时滞;三是输入饱和.前人对于这3个问题的单独研究不少,但3个问题的综合研究并不多.文献[2]综述了近年来抗饱和的研究概况.总体上看抗饱和设计方法可分为一步法与两步法,补偿器的选择可分为静态补偿[3]与动态补偿[4],从反馈的角度可分为状态反馈[5]与输出反馈[6].对于具有输入饱和的时滞开关线性系统,文献[7]利用动态补偿方法给出了闭环系统稳定的充分条件.针对一类具有输入饱和的时滞控制系统,文献[8]以无输入饱和与有输入饱和的系统状态之差作为性能指标,推导出一种使其最小化的动态补偿抗饱和控制器.针对具有输入饱和的时不变仿射非线性系统,文献[9]利用T–S模型、输出反馈、并行分布补偿及矩阵理论,得到了闭环系统稳定的线性矩阵不等式(linear matrix inequality,LMI)判据.

现实系统中的时滞现象是多样的,主要体现在时滞函数的约束条件上,不同的约束条件代表着不同的时滞问题[10–12].文献[13]针对一类时滞变化率有界的饱和时滞非线性系统设计了静态抗饱和补偿器,利用Lyapunov泛函重新构造了利布希茨连续性条件,得到了全局及局部稳定条件.针对具有饱和的分布正常数时滞神经网络系统,文献[14]利用经典的两步法提出了一种代数抗饱和补偿设计.所谓两步法[15]是指:第一步,在不考虑系统输入饱和的前提下,设计好反馈增益矩阵;第二步,当系统存在输入饱和时,引入抗饱和补偿项并求解补偿增益矩阵.本文使用的一步抗饱和法,能够一步求解出反馈增益阵和补偿增益阵,较之两步法,一步抗饱和能够得到更为全局优化的吸引域估计.

本文研究了一类时滞变化率上确界小于1的饱和时滞非线性系统,当系统状态满足一定条件时[16],饱和时滞非线性系统可利用T–S模糊模型(T–S模型)精确重构为若干个线性子系统的加权和,针对每个线性子系统利用动态输出反馈引入并行分布补偿系统,综合得到闭环控制系统.选择一类含有时滞函数的特殊Lyapunov泛函,利用Schur补引理[17]及矩阵不等式理论[18],得到系统的动态输出反馈一步抗饱和控制,利用一个矩阵不等式的等价引理,得到利用间接LMI一步抗饱和补偿算法,一步求出反馈增益矩阵与补偿增益矩阵.仿真实例效果良好.

2 系统描述

考虑如下具有输入饱和的时滞非线性系统:

式中: x(t)∈Rn,u(t)∈Rm和y(t)∈Rp分别为系统的状态向量、输入向量和输出向量,f(x)∈Rn×n,fd(x)∈Rn×n,g(x)∈Rn×m,h(x)∈Rp×n为连续函数矩阵.饱和函数

式中u0i>0(i1,2,···,m)为控制输入的饱和约束.时变时滞τ(t)满足

式中ε是标量,利用T–S模型对系统(1)进行重构.

规则Ri:如果z1(t)为Fi1,z2(t)为Fi2,···,zs(t)为Fis,则

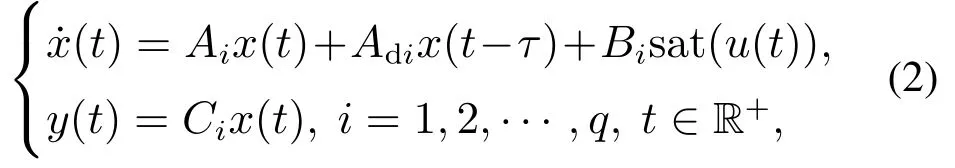
式中:Fij(i1,2,···,q,j1,2,···,s)为规则Ri的第j个模糊集,zj(t)为前件变量,q为规则数,时不变矩阵Ai∈Rn×n, Adi∈Rn×n, Bi∈Rn×m, Ci∈Rp×n分别为第i个线性子系统的状态矩阵、时滞矩阵、输入矩阵以及输出矩阵.

则系统(1)可被重构为

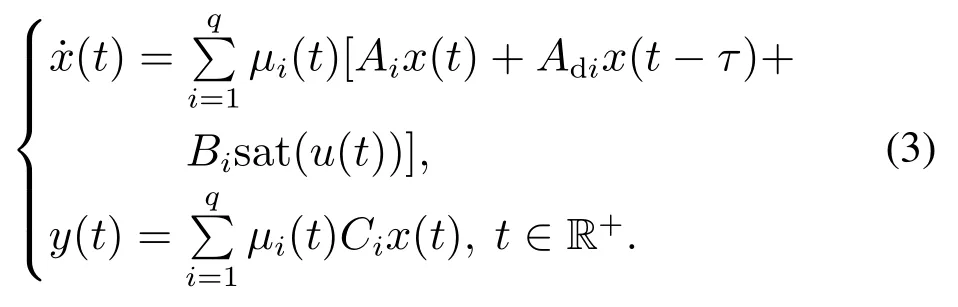
式中:Lb为n维行向量,db>0为常数.考虑隶属度函数集合

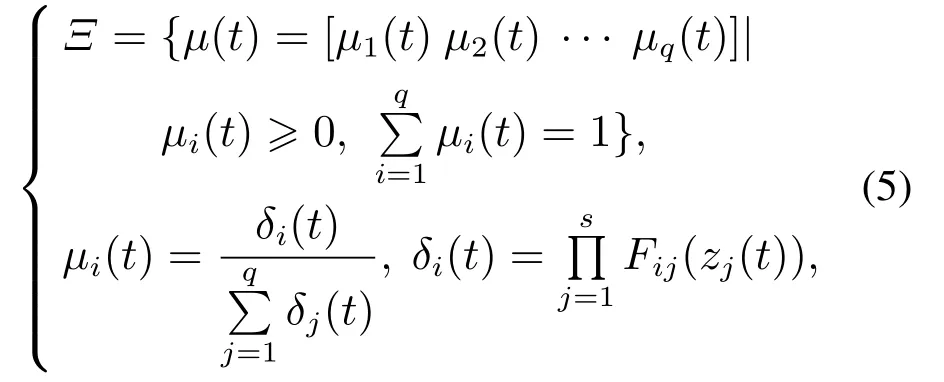
式中:Fij(zj(t))表示前件变量zj(t)在模糊集Fij中的隶属度,容易证明,如果x(t)∈Ω(x),则存在µ(t)∈Ξ使得系统(1)可以用系统(3)精确重构.

引入nc维并行分布补偿系统

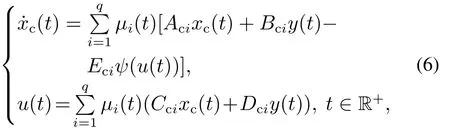
式中:xc(t)∈为并行分布补偿系统的状态变量,ψ(u)u −sat(u)为死区函数,Aci,Bci,Cci,Dci为反馈增益矩阵,Eci为抗饱和增益矩阵.综合式(3)、式(6)可得闭环系统:

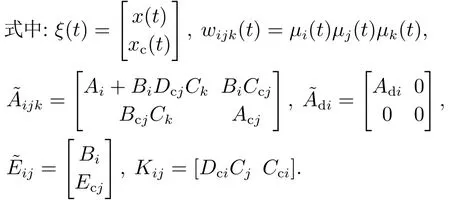
问题1求出使得闭环系统(7)局部渐近稳定的矩阵Aci,Bci,Cci,Dci,Eci, i1,2,···,nc,并给出闭环系统(7)的吸引域估计及其优化模型.

为了便于问题求解,给出如下假设:

假设1矩阵对(Ai,Bi)可控,矩阵对(Ai,Ci)可观,i1,2,···,q.

3 主要结果

3.1 控制器设计

设K(a)代表矩阵K 的第a 行构成的行向量,KT(a)(K(a))T,符号∗为对称矩阵左下角对称块的缩写,为复数v的共轭,简记ξ(t)为ξ,设矩阵Gij与Kij同型,Kij−Gij,定义多面体集

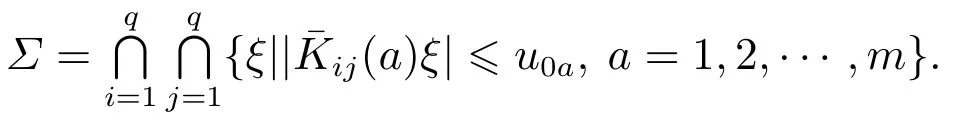
为了便于定理证明,首先给出两个引理.

引理1若ξ ∈Σ,则

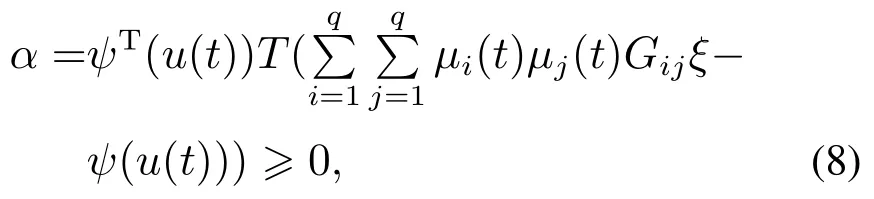
引理2对任意合适维矩阵X,Y(Y >0),Z,有[18]

设对称正定矩阵P,Q,矩阵Nij可写成分块形式:

定理1若存在两个对称正定矩阵P,Q,定义如上,对角正定矩阵T1及合适维矩阵Aci,Bci,Cci,Dci,Eci,Nij,使得

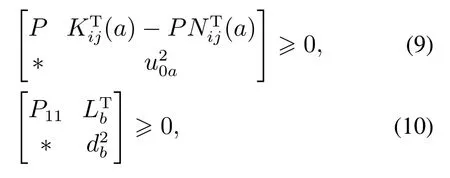
设T1T−1,利用合同变换的性质,对式(11)分别左乘、右乘diag(P,T)得Ψijk<0,i,j,k1,2,···,q,当ξ所以闭环系统(7)在区域0时,所以闭环系统(7)在区域Λ内渐近稳定.证毕.

3.2 间接LMI一步抗饱和补偿算法

为了便于结论推导,首先给出如下引理.

引理3已知对称矩阵Γ ∈Rn×n和两个矩阵X ∈Ri×n, Y ∈Rj×n,则存在一个合适维矩阵Θ使得

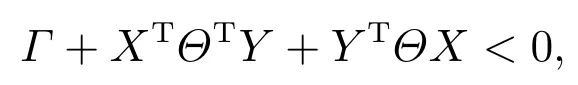
当且仅当

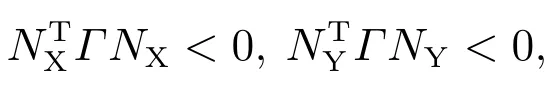
式中NX和NY分别为由零空间ker(X)和ker(Y)的任意一组基向量作为列向量构成的矩阵[19].

引理4矩阵P,Q定义如上,若P11和Q11正定,P12列满秩,且

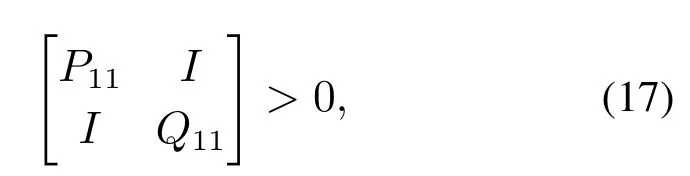
则P,Q正定.

那么a11<0与b11<0不能同时成立,所以式(14)无解.同理可证,如果存在(Ai,Ci)不可观,那么式(15)也无解.

3.3 吸引域估计及其优化模型

由定理1知闭环系统(7)的一个吸引域估计为Λ,由于笔者真正感兴趣的是原系统(1)的吸引域,因此,仅考虑区域Λ与x(t)向量空间的交空间{x|xTP11x1},以矩阵P11的最大特征值λmax的最小化为优化目标,考虑如下优化模型:

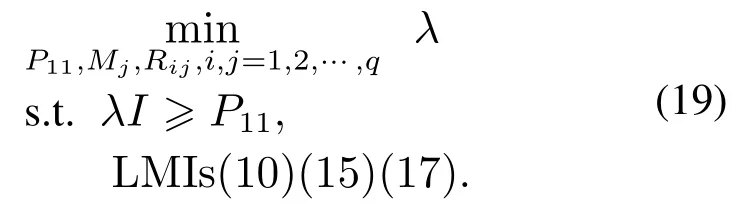
间接LMI一步抗饱和补偿算法中的步骤2做出如下改变就能得到优化算法.

步骤2求解式(19)得到矩阵P11,Mj,Rij,λ, i,j1,2,···,q.

4 数值仿真

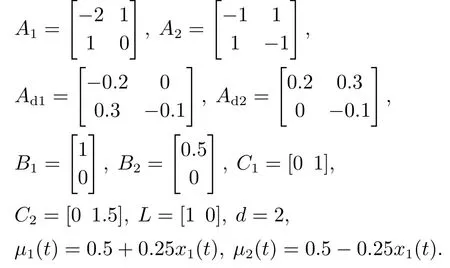
结合求解结果,可得闭环系统(7)的状态图如图1所示,闭环系统优化前后的吸引域如图2所示.

图1 闭环系统(7)的状态图Fig.1 The states diagram of closed-loop system(7)

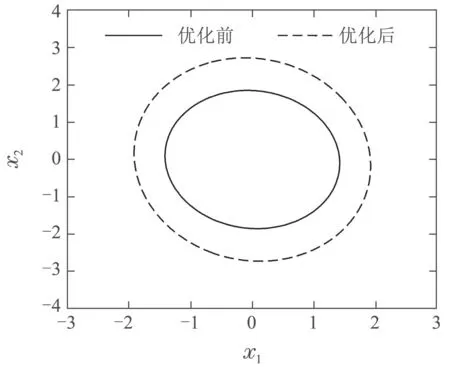
图2 闭环系统(7)的吸引域对比图Fig.2 The comparison chart of attraction domain in closed-loop system(7)

由图1可知,4 s后,系统状态趋于0,达到稳定状态,间接LMI一步抗饱和补偿算法起到了明显的控制效果.由图2可知,优化模型(19)起到了较为显著的优化作用.

5 结论

本文研究了一类时滞变化率上确界小于1的饱和时滞非线性系统的抗饱和设计.首先利用T–S模型对时滞非线性系统精确重构,再利用动态输出反馈引入并行分布补偿系统,综合得到闭环控制系统.然后,利用Lyapunov稳定性理论、扇形区间不等式、Schur补引理、矩阵不等式的等价引理以及矩阵合同变换等理论,得到间接LMI一步抗饱和补偿算法及吸引域优化模型,实现了一步求解反馈增益矩阵和补偿增益矩阵的目标.最后进行了数值仿真,仿真结果验证了本文提出的抗饱和设计的有效性.