双积分器的有限时间积分滑模设计及应用

吴金尘,刘 俊,叶华文

(中南大学自动化学院,湖南长沙 410083)

1 引言

滑模控制处理不确定系统时具有鲁棒性强的特点,已经被广泛应用于实际工程中[1–3].相较于传统滑模控制,积分滑模控制由于增加了积分项,可消除加性扰动的影响.

最初,Utkin提出积分滑模设计的基本方法[4],随后,国内外很多学者开展了多方面的研究[1,5–6].Cao等人在文献[4]的基础上给出了具有匹配和非匹配扰动的非线性系统的积分滑模控制方案[7–8].积分滑模控制系统的动态性能主要取决于滑模面与积分项的选取.李鹏等人设计了一类具有“小误差放大,大误差饱和”功能的光滑非线性饱和函数来重设积分滑模面[9].

近年来,已经有学者将有限时间稳定与积分滑模结合着展开研究.比如Nair等人提出了基于积分滑模的鲁棒有限时间事件触发控制策略,利用快速到达定律来提高收敛速度,并适用于具有模型不确定性干扰的系统[10].Laghrouche等人针对不确定非线性系统,基于积分滑模提出了一种高阶滑模控制方案,解决了有界不确定性的高阶输入输出系统的有限时间镇定问题[11].上述两个工作均研究模型不确定干扰的情形.

本文在文献[4]的基础上,针对一类具有加性扰动的双积分器,受嵌套饱和控制的启发,设计一种新的积分滑模面,实现受扰双积分器的有限时间镇定.相对文献[4]而言,本文的积分滑模面表达式中有分数指数,在参数选择上可能出现奇异性.有趣的是,利用Haimo[12]有限时间稳定原理,可证明,虽然积分滑模面含有分数指数,但因为滑模面的合理设置,不会产生奇异性.

本文余下部分的内容安排如下:第2节给出几个重要引理,为后面滑模面与控制器的设计提供理论基础;第3节针对带加性扰动的双积分器,给出新滑模面及控制器的设计;第4节将本文算法应用于直流电机角速度控制系统.

2 准备工作

本节给出几个重要引理.

引理1[12]假设是有限时间稳定的Lipschitz连续系统,x ∈Rn,g(0)0.若x(t)在tT <∞到达原点,那么

引理2[13]为双积分器系统选取嵌套饱和控制器

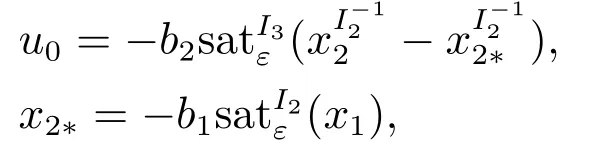
其中Ik(k1,2,3)为

若b1,b2满足

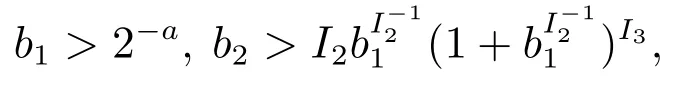
则控制器u0有限时间镇定上述双积分器系统.

3 有限时间积分滑模控制设计

本文考察如下带加性扰动的双积分器

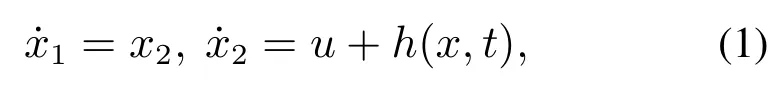
3.1 基本设计过程

根据文献[4]的积分滑模设计思想,为系统(1)设计控制输入

其中: u0代表理想控制,u1为抵消不确定加性扰动h(x,t)的不连续控制.积分滑模面s设计为传统滑模面只设置s0,现在增加变量z是为了消除加性扰动的影响.

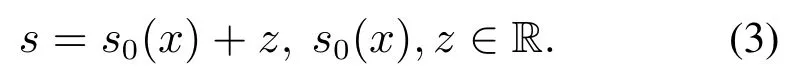
假设u1u1eq−h(x,t),且使变量z的动态方程满足

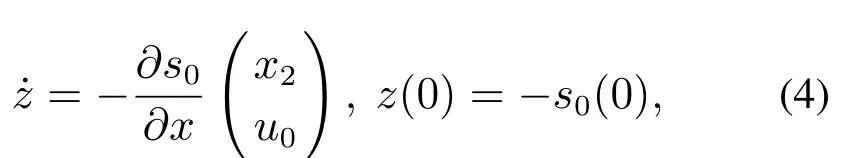
当u1−h(x,t),应设置合适的u1趋使系统状态到达滑模面.具体过程如下:

2)s(u1+h(x,t))<0;

3)方程(4)的非奇异.

3.2 积分滑模面设计

与传统积分滑模中用状态的线性组合不同,现在的滑模面表达式中出现了分数指数.特别是,将出现负的分数指数.

直接计算有

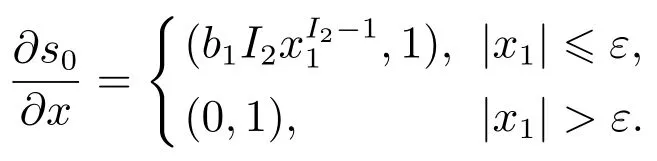
下面说明方程(4)不会因为负分数指数而导致奇异性.

此时I2−1是负分数指数,必须审慎讨论是否出现奇异性,也即是否会出现“除零”的现象.对此,本文利用Haimo的有限时间稳定原理给出相关解释.

首先,根据引理2,下面的控制器有

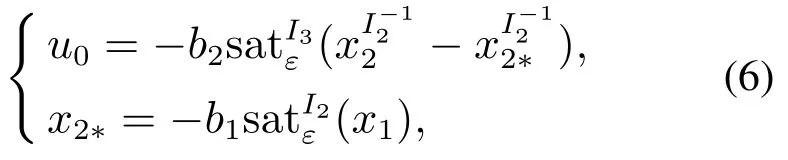
即x2(t)比x1(t)更快地收敛到零.注意到

又知道x1(t)比更快地收敛到零.因此,是非奇异的,所以变量z的动态方程(4)是合理的.

3.3 控制器设计

当u1控制器设计−h(x,t)时,设置不连续控制器u1保证条件2成立.具体地,令

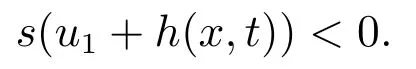
至此,本文给出了整个积分滑模设计,由式(2)–(7)描述.

结合理想控制器,最终的控制器为

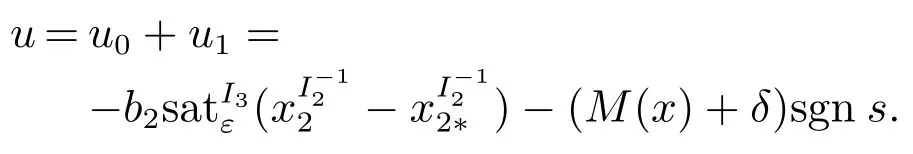
3.4 有限时间稳定分析

下面证明整个积分滑模设计保证状态x1,x2有限时间收敛到原点.以下是简单的分析过程.

首先,对于系统(1),若设置积分滑模控制(2)–(7),则系统状态在有限时间达到积分滑模面.事实上,选取Lyapunov函数直接计算有

这也意味着该积分滑模面是有限时间可达的[14].

至此,证明了系统状态于有限时间到达滑模面,而滑模面上的动态系统又有限时间收敛到原点.总结起来,得到本文的主要结论.

定理1为系统(1)设计积分滑模控制(2)–(7),则系统状态x1,x2有限时间收敛到原点.

李小树在电话里说，他已经在柳江古镇的下游找到许春花了。我迷糊中忘记了许春花是谁。李小树提醒我说：“就你在柳江古镇采风时在镇口那棵黄桷树下逗着洋娃娃的许春花。”

4 在电机系统上的应用

就实际工程控制系统而言,电机控制是一个相当活跃的研究课题[15–21].下面处理一类带减速机的直流电机角速度控制系统[16],作为本文所建议的算法的应用.

4.1 直流电机角速度控制系统的模型

所考察系统的模型图如图1所示.图中:i代表电感电流也就是电枢回路电流,u是施加在电枢电路输入端子上的电压,可以作为整个电路的控制输入,w1表示减速机输出轴的角速度,L和R分别表示电枢电阻和电感,ke和km分别表示电动势常数和电机转矩常数,n是减速机速降,J0和J1分别表示电机转子转动惯量和减速机转子转动惯量.另外,τL表示有界负载转矩,p0和p1分别表示电机粘性阻尼系数和减速机自身粘性阻尼系数.

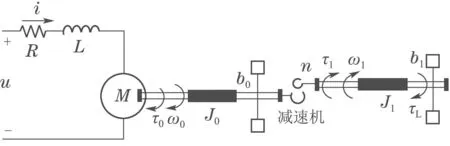
图1 带减速机的直流永磁电机模型Fig.1 DC permanent magnet motor model with reducer

由电路方程与力学方程可得如下数学模型:

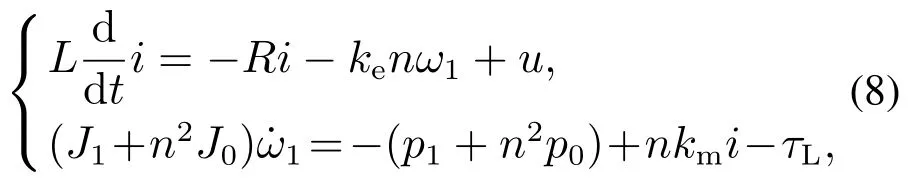
以减速机输出轴的角速度ω1和角加速度作为状态变量,令JeqJ1+n2J0,peqp1+n2p0,记系统输出为yω1,直接计算得到

这里ξ作为时变转矩干扰,满足

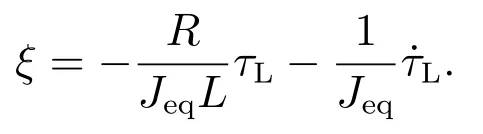
当有界负载转矩τL满足利普希茨连续条件时,时变转矩干扰ξ有界.

4.2 积分滑模控制器的设计

其中积分滑模面为

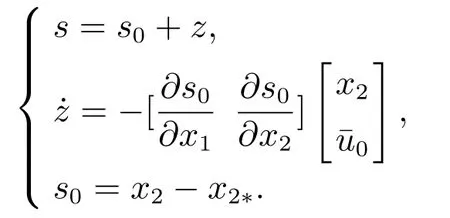
根据定理1,整个闭环系统是有限时间稳定的.

4.3 仿真分析

该电机控制系统的参数如下[16]:

km82.2 mN·m/A,n81.

不妨令负载转矩τL2(1 −e−5t)N·m,则

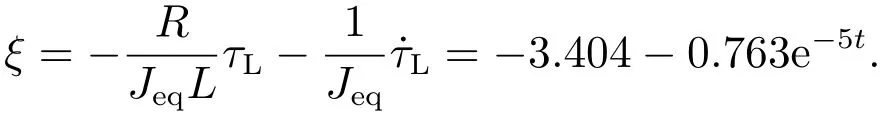
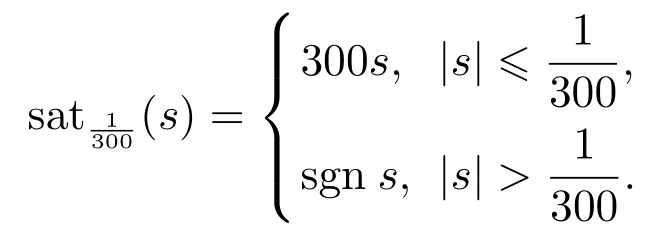
选取初始状态和控制参数为

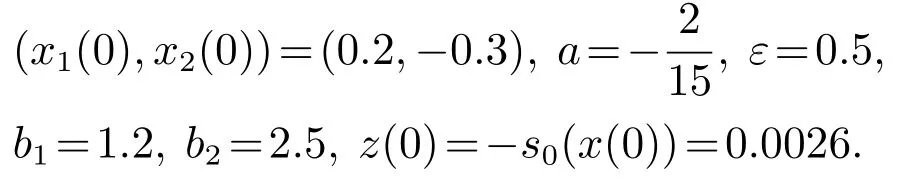
仿真结果如图2–3所示.

直流电机稳态运行时,减速机角速度与角加速度应为0,电动机能以稳定的角速度运转,这是本文最终需要的结果.仿真结果表明,积分滑模控制能在有限时间使直流电机角速度控制系统状态快速收敛到平衡点.

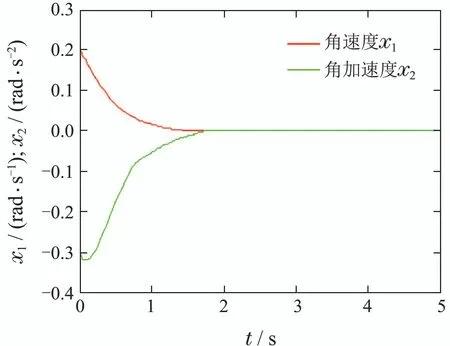
图2 系统(11)的角速度与角加速度状态轨迹Fig.2 Angle velocity and angular acceleration state trajectory of system(11)

图3 系统(11)的控制输入轨迹Fig.3 Control input trajectory of system(11)

5 结论

本文针对一类具有加性扰动的双积分器,在文献[4]的研究基础上设计了一类新的含有分数指数的积分滑模面,不仅消除了加性扰动的影响而且保证滑模上的动态有限时间稳定.而利用Haimo的有限时间稳定原理,本文证明了:虽然积分滑模面设计中出现分数指数,但滑模动态不会出现奇异性.通过直流电机控制系统实现了角速度的快速控制,验证了该种方法的有效性.