基于变分模态分解和支持向量机的滚动轴承品质评估

郝 勇 ,吴文辉 ,商庆园

(1.华东交通大学机电与车辆工程学院,江西南昌 330013;2.浙江众合科技股份有限公司,浙江杭州 310051)

1 引言

滚动轴承作为机械设备的关键基础部件,用于支撑机械旋转体来降低设备在传动过程中的机械载荷摩擦系数[1].不同工况下应选用不同精度等级的轴承,而相应精度等级的轴承应满足国家标准或行业标准规定的相应精度技术参数要求,否则会影响机械设备的运行精度[2].轴承品质等级的划分采用《JB/T 7047–2006中深沟球轴承振动水平标准》执行,根据振动加速度级峰值将轴承品质分为优等品、一等品和合格品.轴承的振动信号具有非线性、非平稳和缺陷特征微弱的特点,从振动信号中直接提取轴承的特征较困难且不准确,因此,需要探索新的轴承振动信号的信息提取方法,进一步增加或强化反映轴承振动信号的特征指标信息,实现轴承品质等级的在线实时自动化分拣.

国内外关于轴承的研究主要集中于其在旋转机械中的故障诊断.尚长沛等[3]提出基于经验模态分解(empirical mode decomposition,EMD)和自回归模型(autoregressive model,AR)的轴承故障检测方法,实验结果证明其有效性,然而,EMD高度依赖于极值点搜寻方法,从而导致对噪声和采样频率高度敏感;张琛等[4]提出基于共识经验模态分解(ensemble empirical mode decomposition,EEMD)奇异值熵的轴承故障检测方法,该方法成功识别轴承故障,但是EEMD中的加性白噪声会对信号重建干扰、使计算效率降低;Gong等[5]基于变分模态分解(variational mode decomposition,VMD)方法对轴承的故障信号进行分析并与EMD和EEMD方法进行比较,结果表明VMD方法在故障特征检测方面具有较好的性能;Mohanty等[6]针对轴承信号特征提取困难的问题,提出了基于VMD、相关系数和赫斯特指数结合的方法,成功提取故障特征.Ren等[7]提出了VMD结合多尺度排列熵的轴承品质评估方法,实验结果证明了其有效性.因此,VMD方法在信号处理方面要优于EMD/EEMD等信号处理方法.排列熵(permutation entropy,PE)是一种检测时间序列随机性和动力学突变的算法,具有计算简单、抗噪声能力强等特点,对信号的变化具有很高的敏感性.

综上所述,目前采用模式识别方法对轴承品质等级进行识别的相关研究较少.本文针对6201型滚动轴承品质评估过程中振动信号特征提取和品质等级识别方法展开研究,提出了基于时域指标(time domain indexs,TDI)和VMD–PE的滚动轴承特征提取方法,并结合模式识别方法建立轴承品质等级的评估模型,实现轴承品质等级的在线识别.

2 算法理论介绍

2.1 变分模态分解

VMD算法是一种完全非递归、自适应、准正交的信号分解方法,它将调制信号分解成多个有限带宽模态函数uk,利用多个维纳滤波组实现滤波.在信号分解时,每一个模态函数uk都围绕着一个中心频率ωk进行分解.每一个模态函数都有有限的带宽,为得到模态函数的带宽,需要进行如下步骤:

1)对每个模态函数进行Hibert变换,得到每个模态函数的解析信号:

2)通过对各自估计的中心频率进行指数修正,将模态函数的频谱转移到各自的基频带:uk(t)]e−jωkt;

3)计算步骤2中的信号的梯度的平方L2范数,估算出各个模态函数的带宽,对应的约束问题变为

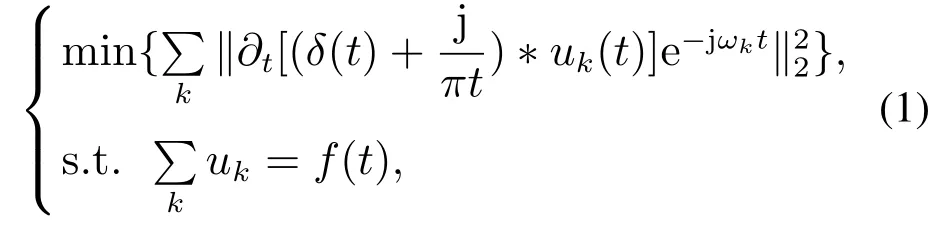
式中:uk表示求取的有限带宽模态函数(band-limited instrinsic mode function,BIMF)分量,

ωk为BIMF分量的中心频率,ωk{ω1,ω2,···,ωK};δ(t)为单位脉冲函数;∂t为函数关于时间t的偏导数;j为虚数单位;“*”为卷积符号.

为解决此约束问题,考虑了二次惩罚函数α和拉格朗日乘数λ相结合的方法.这两项的组合既可以执行了拉格朗日乘数的约束性,又具有完美的收敛性.通过以上两项的引入,可以将式(1)中带有约束条件的变分问题转化为无约束条件的变分问题进行求解:

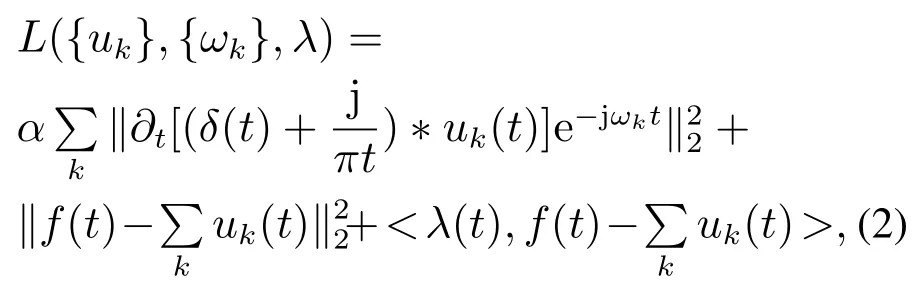
式中:α为带宽参数;λ(t)为拉格朗日乘子.这样式(1)中的最小化问题就可以转化为增广矩阵式(2)中的鞍点问题,通过交替方向算法(alternating direction method of multipliers,ADMM)的迭代次优化序列[8–9],得到其模态分量和中心频率表达式分别如下:

2.2 排列熵计算

熵值是物理学的概念,用来度量系统的紊乱程度,熵值越大,表示系统越复杂.排列熵是Bandt和Pompe提出的一种定量描述时间序列复杂程度的非线性估计方法[13].排列熵计算方法简单,运算速度快,计算值稳定并且抗噪声能力强.排列熵的计算步骤如下.

给定一组时间序列X{xk,k1,2,···,N},首先对其进行相空间重构,可以得到时间i的m维向量

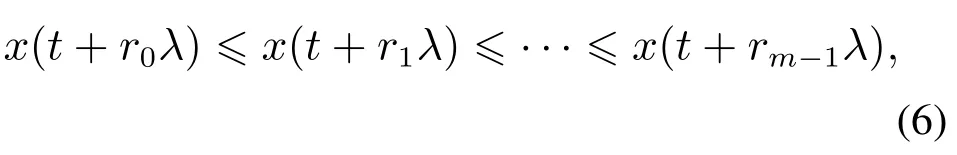
因此,对任意一个Xi都有m!种排列方式,定义其相对分布频率为

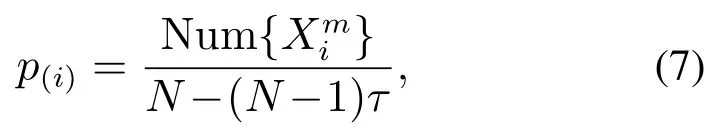
排列熵可以定义为

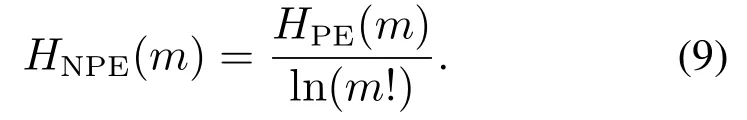
由此可知,HNPE(m)满足0HNPE(m)i1.

从以上过程可以看出,HNPE值越大表明时间序列随机性越大越不规则,相反,HNPE越小表明时间序列越规则,更具有周期性.在极端情况下,假如时间序列是一组白噪声,则HNPE为1;若时间序列为正弦或者余弦等情况下,则HNPE为0.因此可以用排列熵值来估计给定时间信号的复杂性和动态变化[14–15].

根据定义可知,排列熵值的计算受到嵌入维数m和延迟时间τ的影响较大,m太小则重构的时间序列太少,无法进行熵值计算;m太大,计算时间太长,导致效率低下.相同的,若τ太小,重构的相邻延迟坐标的差别太小,失去了重构的意义;若τ太大,会导致重构相邻坐标的相关性降低,丢失信号原有的特征信息.针对此问题,Bandt等人[16]建议在进行排列熵值计算时一般m取值3到7之间,τ取值小于2.

2.3 支持向量机

支持向量机(support vector machines,SVM)是由Vapnik等人提出,属于有监督学习算法,是建立在结构风险原则基础上和统计学习理论的VC维理论的一种机器学习算法.适用于小样本、非线性和高维度数据.在进行分类时,支持向量机算法通过构建分类超平面,将空间的样本分离,并取得最大边缘.

对于线性可分数据集,SVM通过间隔最大化或等价求解相应的凸二次规划问题,得到分离超平面为

式中:x为样本数据;w为法向量;b为截距.相应的分类决策函数为

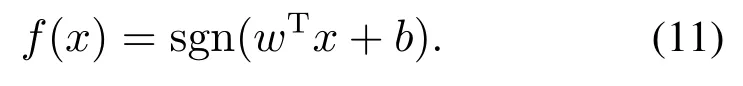
对于线性不可分数据集,通用的方法是引入松弛变量ξ,则线性不可分问题转化为如下优化问题来表示:

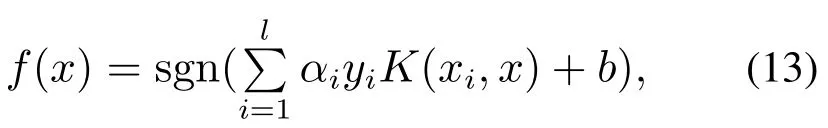
式中:α为拉格朗日乘子,K为核函数.常用的核函数有线性核函数、d阶多项式核函数、径向基核函数和具有参数k和θ的Sigmoid核函数[17].

网格搜索法(grid search,GS)的基本原理是让C和g在一定的范围划分网格并遍历网格内的所有点进行取值,对于获得的C和g使用K阶交叉验证的方法得到对应训练集的分类准确率,取使得训练集分类准确率最高所对应的C和g为最佳参数[18].

3 滚动轴承品质评估方法及评价

3.1 滚动轴承品质评估方法

本文利用VMD可以对振动信号进行细分和排列熵计算简单、抗噪声能力强等优点,提出了滚动轴承品质等级评估方法,具体流程如图1所示.

图1 滚动轴承品质评估流程示意图Fig.1 Schematic diagram of rolling bearing quality evaluation process

该方法主要包括信号获取、特征提取和状态识别3个环节,具体步骤为:

①依据机械行业推荐标准—–深沟球轴承振动水平收集3个品质等级的轴承样品各50个,采用自主设计的测试装置获取不同品质等级轴承的振动信号;

②对采集的振动信号进行时域分析(有效值、峰值指标和峭度指标),利用VMD算法将振动信号进行分解得到若干个BIMF分量,并计算每个BIMF分量的PE值;

③将提取的时域特征和VMD–PE值组成特征输入矩阵进行SVM模型的构建,最后对未知滚动轴承的品质等级进行评估.

3.2 模型的评价标准

采用测试集的识别率评价模型的优劣.其中识别率越高,表明模型越好;识别率越低,表明模型越差.Accuracy×100%,式中:Accuracy表示识别率,p为正确识别样本数,t为总样本数.

4 实验部分

4.1 轴承振动信号的采集

依据《JB/T 7047–2006中深沟球轴承振动水平标准》,根据加速度级峰值将轴承品质分为优等品、一等品和合格品.轴承品质在线检测流程及振动测试工位示意图如图2所示.

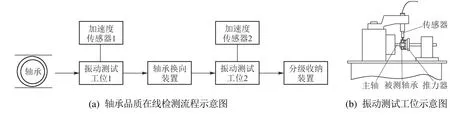
图2 轴承品质在线检测流程及振动测试工位示意图Fig.2 On-line testing process of bearing quality and schematic diagram of vibration testing station

主轴转速设定为1800 r/min,推力器轴向载荷选定70 N,采样频率为8 kHz.在进行检测时,需要对轴承正反面进行信号采集,将两次采集信号的平均值作为轴承的检测信号.图3为采集的3种品质轴承的振动信号图.

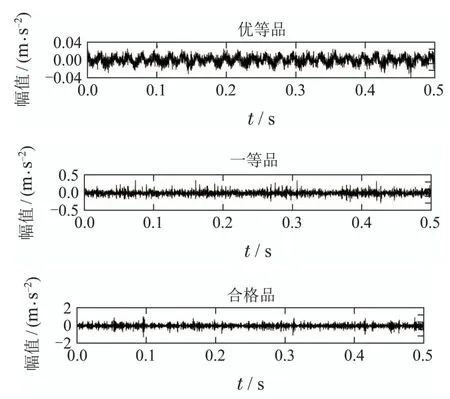
图3 3种品质轴承振动信号图Fig.3 Vibration signal diagrams of three quality bearings

4.2 滚动轴承振动信号的时域分析

时域分析可以直观的反映出轴承振动信号随时间的变化.分别选取有效值、峰值指标和峭度指标作为轴承振动分析的时域特征.有效值用于描述振动信号的能量,当轴承产生异常后,其振动增大,能量增强.峰值指标是用于检测振动信号是否存在冲击的统计指标.通常峰值是指单峰最大值,但是在振动信号中它是一个时不稳参数.峭度是概率密度分布尖峭程度的度量,是无量纲参数.它反映了振动信号的冲击特征,正常情况下振动信号的峭度值为3左右,如果接近或者超过4,则说明存在冲击性振动[19].

表1所示为6201型轴承代表样本的时域分析特征参数值.

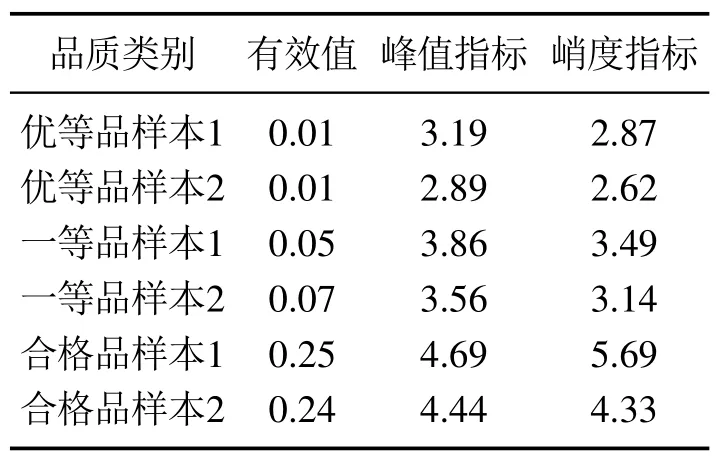
表1 6201型轴承代表性样本时域分析特征参数值Table 1 Characteristic parameter values of the typical sample of type 6201 bearing in time domain

由表1可以看出优等品轴承的有效值、峰值指标和峭度指标都相较于一等品和合格品较小,说明优等品轴承振动信号平稳,峭度值接近于3,说明轴承正常.一等品轴承有效值相较于优等品轴承稍大一点,说明一等品轴承振动信号振幅变大,信号能量增强,其峭度值稍大于3且小于4,说明轴承正常.合格品轴承的有效值较大,且峰值指标都大于优等品和一等品,说明存在冲击信号,峭度指标都大于4,说明轴承存在冲击性振动,这类轴承只能用于对轴承自身振动要求较低的机械中.

4.3 滚动轴承振动信号的VMD及排列熵分析

利用VMD算法对3种品质轴承振动信号进行分解,得到的BIMF函数,再对BIMF函数进行频谱分析.根据文献[20–21],取

得到4 个固有模态(intrinsic mode function,IMF)分量函数,按照低频到高频排列得到分解结果.图4为不同品质轴承信号的VMD分解结果图以及频谱分析图.通过3类轴承的频谱分析图可以看出,同种品质的轴承各BIMF函数频率分布不同,不同品质轴承对应的BIMF函数频谱分布相似,但频谱幅值不同.通过VMD分解,可以提取不同品质等级的轴承的频率,从而可以消除外界噪声的影响.然而,无法直接利用BIMF分量函数的频谱图进行轴承品质等级的判别,因此,需要对BIMF分量进行排列熵的计算以进一步获取其综合的统计信息.

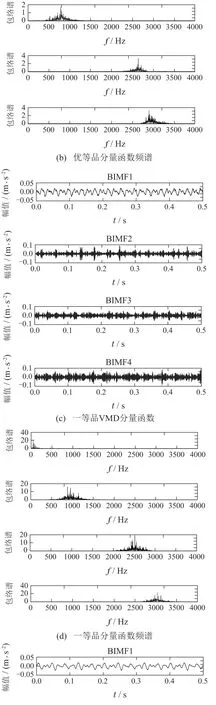
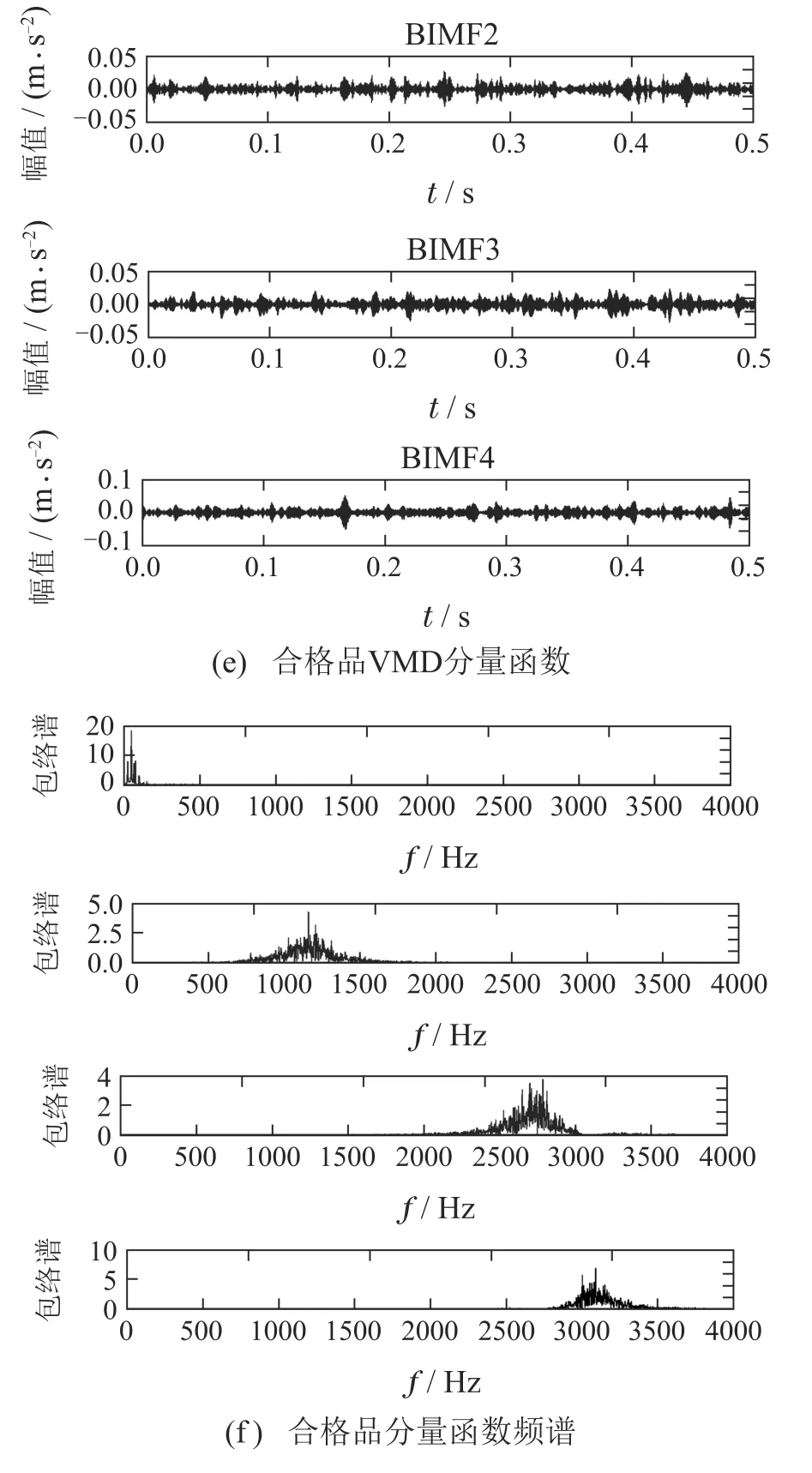
图4 3类品质轴承的VMD分量函数图和分量函数频谱图Fig.4 VMD’s BIMFs diagrams and frequency spectrums of three kinds of quality bearings

图5所示为优等品、一等品和合格品各50个轴承样本经VMD分解后BIMF函数的排列熵统计图.

图5(a)中横坐标为BIMF分量,纵坐标为各BIMF分量的排列熵值,其中优等品为圆圈,一等品为星号,合格品为三角形.通过排列熵分布图可以看出优等品的BIMF1排列熵值集中在1到2之间且值都小于一等品和合格品BIMF1的排列熵值,BIMF2的排列熵值集中在2.5到3之间较一等品和合格品偏小,BIMF3的排列熵值分布在3到4之间与一等品和合格品的熵值大致相同,BIMF4的排列熵值优等品与合格品基本一致且都小于一等品.将3种品质轴承的BIMF分量的排列熵值进行平均计算得到如图5(b)的柱状图,通过柱状图可以清楚的看出不同品质的BIMF1和BIMF2函数的排列熵值差异较大,其中优等品的排列熵值最小,一等品次之,合格品的排列熵值最大.但是,BIMF3和BIMF4函数之间的排列熵值差异较小,这是因为BIMF函数是按照低频到高频排列,低频段时时间序列随机性小且规则符合排列熵的特点,但是高频段时由于随机噪声的影响,使其排列熵值的顺序没有呈现出规律性变化[22–23].因此BIMF函数的排列熵值可以作为轴承品质评估的判断条件之一.

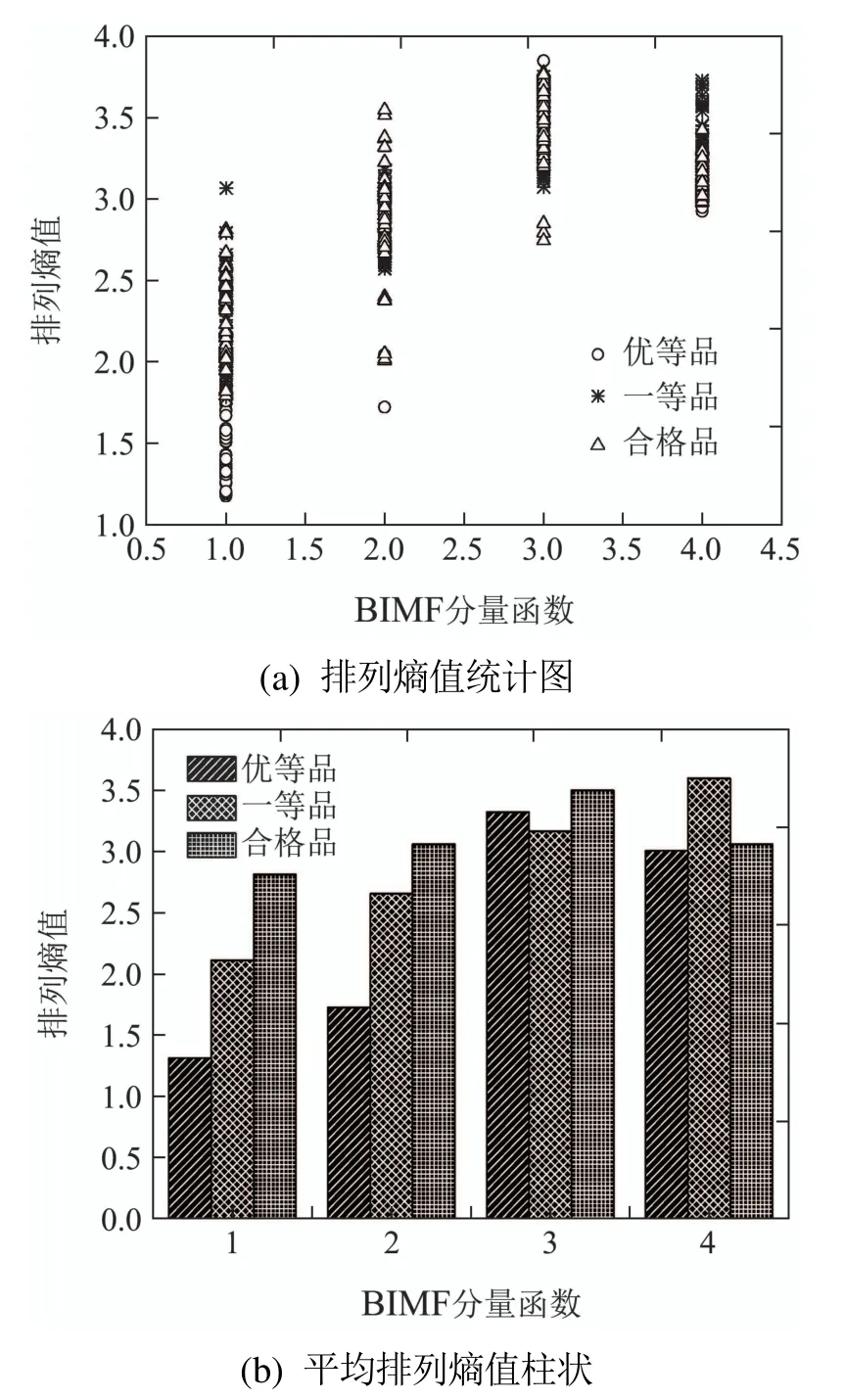
图5 3类品质轴承的分量函数排列熵值图Fig.5 BIMFs’ permutation entropy values of three kinds of quality bearings

4.4 滚动轴承品质评估模型的建立

4.4.1 基于时域特征结合PE和结合VMD–PE的滚动轴承品质评估

采集3种品质等级的滚动轴承共计150个样本的振动信号,采用均匀取样的方法按照3:2的比例分别分为校正集和测试集,其中校正集90个样本用于品质评估模型的建立,测试集60个样本用于验证模型.SVM方法用于品质评估模型的构建,其中,SVM采用的核函数为径向基核函数(radial basis function,RBF),惩罚参数C和核函数参数g则是通过GS寻优方法获取最优值[24].

以3种品质等级轴承振动信号的时域特征(有效值、峰值指标和峭度指标)及其PE值作为SVM模型的输入特征矩阵建立模型,并进行测试,测试集样本的识别率为83.33%,SVM的惩罚参数C为2.83,核函数参数g为3.20.

以3种品质等级轴承振动信号的时域特征(有效值、峰值指标和峭度指标)及其VMD分解后4个BIMF分量的PE值作为SVM模型的输入特征矩阵建立模型,并进行测试,测试集样本的识别率为93.33%,SVM 的惩罚参数C为4,核函数参数g为5.67.

4.4.2 最优判别模型分析

两种方法分析结果如表2所示,由表可知,对于6201型轴承,振动信号时域指标和VMD–PE的SVM模型可以得到比时域指标和PE的SVM模型更好的识别率,识别率由83.33%提高到93.33%,识别结果如图6所示,其中优等品中1个样本识别错误,合格品中有3个样本识别错误,一等品全部识别正确.VMD算法将一个信号分为4个模态分量,将信号的细节信息进行分离,经计算后的特征信息进一步增加和强化,SVM 算法会依据每一个特征的重要性给予相应的权重进行模型的构建,使其识别结果更加准确、可靠.因此,基于时域特征结合VMD–PE的滚动轴承品质评估方法可以较好地实现其品质等级的实时在线评估.

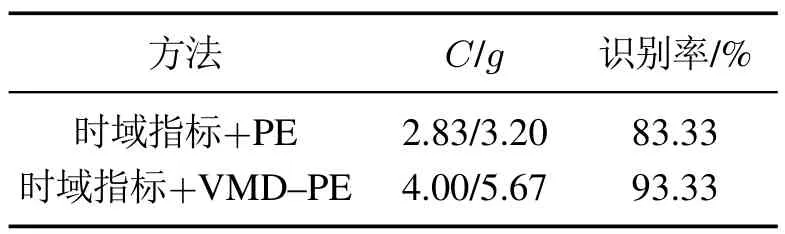
表2 基于SVM模型的轴承品质评估结果Table 2 The results of bearing quality evaluation based on SVM model

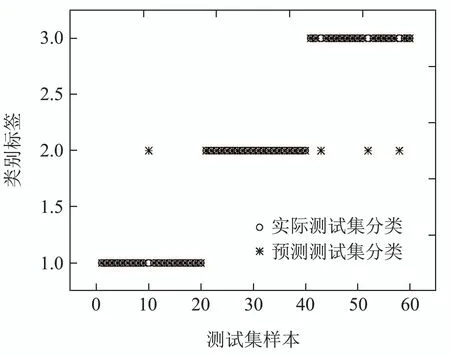
图6 时域特征结合VMD–PE的SVM测试集预测分类图Fig.6 SVM test set prediction classification diagram with time domain features combined with VMD–PE

4.5 公开数据集的方法验证

为了验证本文所提方法的有效性,采用美国西储大学电气工程实验室提供的数据集[25]进行验证.选取在电机负载为0 HP、轴承转速为1797 r/min、采样频率为12 kHz情况下风扇端轴承的4种状态(正常状态、内圈故障、外圈故障以及滚动体故障)数据各50组,共计200个样本.采用均匀取样的方法按照3:2的比例分别分为校正集和测试集,其中校正集120个样本用于品质评估模型的建立,测试集80个样本用于验证模型,分别对4种状态的轴承信号计算有效值、峰值和峭度值3个时域指标;然后采用VMD方法将信号分解为4个BIMF,并分别计算其PE值.将3个时域指标和4个PE值共计7个特征作为SVM的输入变量构建轴承品质等级预测评估模型.其预测结果为100%.

5 结论

针对滚动轴承优等品、一等品和合格品品质在线评估难的问题,提出了基于滚动轴承振动信号时域特征结合PE与基于滚动轴承振动信号时域特征结合VMD–PE的SVM两种在线品质评估方法.实验结果表明,基于滚动轴承振动信号时域特征结合VMD–PE的SVM在线品质评估方法具有较好的正确识别率(93.33%).该方法有望成为滚动轴承的品质等级在线评估的有效方法.