磁悬浮控制敏感陀螺转子偏转通道稳定控制方法

夏长峰 ,蔡远文 ,任 元 ,贾蕊溪 ,李 楠

(1.西安卫星测控中心,陕西西安 710043;2.航天工程大学研究生院,北京 101416;3.航天工程大学宇航科学与技术系,北京 101416;4.人因国防工程重点实验室,北京 100094;5.63961部队,北京 100012)

1 引言

随着我国航天事业的飞速发展,对航天器姿态控制系统性能的要求不断提高[1–2],甚稳超静姿态控制技术成为我国卫星系统与控制技术亟待突破的关键技术[3–4],而研制具备高精度力矩输出功能的惯性执行机构是发展甚稳超静姿态控制系统的必然要求[5–6].目前,国内外在轨运行的高精度、多功能、长寿命三轴稳定卫星中,几乎都是使用控制力矩陀螺作为惯性执行机构[7–8],影响控制力矩陀螺系统精度和寿命的主要因素是转子支承[9–10].与传统机械式陀螺相比,磁悬浮控制力矩陀螺(magnetically suspended control momentum gyro,MSCMG)具有无接触、无摩擦、精度高、寿命长等优点[8],是卫星姿态控制系统的理想执行机构.在MSCMG的基础上,文献[11]提出一种磁悬浮控制敏感陀螺(magnetically suspended control&sensing gyro,MSCSG),该陀螺具有一定小角度的微框架能力,能够瞬间输出较大的陀螺力矩,具备MSCMG姿态控制的功能;此外,载体姿态变化时,MSCSG中的磁轴承对转子沿径向施加二自由度控制力矩,通过测量控制力矩可以间接实现姿态敏感.因此MSCSG融合了MSCMG姿态控制、转子式速率陀螺仪姿态敏感的功能,将两种惯性器件合二为一,显著降低了姿态控制系统的体积、重量、功耗和成本.然而,随磁悬浮转子转速升高,转子偏转通道中陀螺效应增强,使转子在径向以进动或者章动的方式运动,破坏转子的稳定性[12–13].因此,对转子系统进行稳定控制是实现MSCSG检控一体功能的前提条件和必然要求.

MSCSG转子系统采用五自由度全主动控制,与现有的MSCMG相比具有其特殊性:一方面,其五自由度悬浮轴承在磁路设计上采用解耦设计,消除了3个平动方向对两个径向偏转方向的耦合,因此转子偏转只受洛伦兹力磁轴承(lorentz force magnetic bearing,LFMB)控制;另一方面,相比于MSCMG通过框架力矩间接驱动转子偏转[14–15],MSCSG通过LFMB对转子系统施加直驱的偏转力矩,转子系统动力学特性发生了变化;此外,为获取较大的转动惯量–质量比,减小飞轮转子的重量,进而减小磁轴承的体积和承重功耗,MSCSG将高速转子设计为扁平结构,而扁平结构转子两径向偏转通道的耦合更强,转子系统受到陀螺效应的影响更为显著.

为抑制磁悬浮转子的陀螺效应,实现稳定控制,国内外学者近年来提出了多种控制方法.董淑成等采用分散PID控制方法对转子系统进行稳定控制,但是该方法在高频段存在相位滞后,无法对高频段的涡动失稳进行有效抑制[16];任元等采用基于分散PID的交叉反馈控制方法有效抑制了转子径向偏转两通道的耦合,实现了对磁阻力磁轴承支承的MSCMG 转子的稳定控制[17];刘峰等采用基于交叉解耦的滑模控制对磁悬浮转子偏转系统进行解耦控制,但是该方法在变结构切换过程中容易引起系统的抖振[18];文献[19]采用逆系统方法实现了陀螺转子的稳定控制,但是该方法对数学模型具有很大的依赖性,当被控对象模型存在不确定性因素时,其控制效果很差甚至不再稳定;线性二次型调节器(linear quadratic regulator,LQR)控制方法[20]、Cholesky分解降秩方法[21]、最小二乘支持向量积解耦方法[22]理论上可以抑制因径向偏转通道间耦合而引起的失稳,但是这几种方法结构复杂且计算量大,不易于工程实现;微几何方法可以对高速转子系统实现高精度高稳定度控制,但该方法抽象、复杂,需将模型变换到几何域中讨论,且算法模型受映射形式约束[23].此外,上述稳定控制方法存在一个共性问题,即针对的被控对象为采用磁阻力磁轴承支承的转子系统;而本文研究对象为采用LFMB支承的扁平MSCSG转子系统,现有的关于LFMB的文献只涉及利用LFMB对转子系统进行力矩输出以及偏转角度控制[24–25],而基于LFMB的转子稳定控制方法未见深入报道.特殊的结构给MSCSG这种新概念陀螺的转子偏转带来了控制挑战.因此,对LFMB支承的磁悬浮转子进行稳定控制具有重要的工程应用价值,MSCSG转子偏转稳定控制方法的有效性有待通过实验进行验证.

由于滤波交叉控制算法原理简单,工程意义明确,因此本文采用基于分散PID的滤波交叉反馈数字控制方案对MSCSG 转子系统进行稳定控制.在建立MSCSG转子偏转通道动力学模型的基础上,引入基于分散PID的滤波交叉反馈控制方法,通过双线性变换推导出所提出控制方法对应的数字差分方程,搭建了以DSP+FPGA为核心的数字控制系统,采用根轨迹法分析了所提出控制方法的稳定性,并通过转子升速实验对该方法的有效性进行了验证.

2 MSCSG转子偏转通道动力学模型

MSCSG结构如图1所示,主要由陀螺房、陀螺转子、轴向磁轴承、力矩器、径向磁轴承、旋转电机、位移传感器构成.其中:径向磁轴承控制转子沿径向两自由度平动;轴向磁轴承控制转子沿轴向平动;旋转电机驱动转子绕轴向高速旋转;力矩器控制转子沿径向偏转;传感器用于检测转子位置信息.

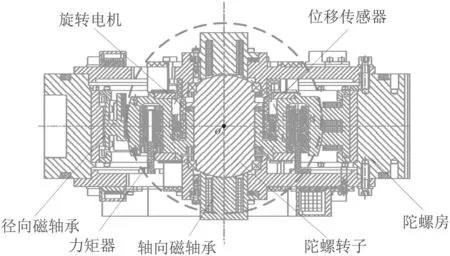
图1 MSCSG结构图Fig.1 Structure diagram of MSCSG

MSCSG转子平动通过纯电磁结构的径向磁轴承和轴向磁轴承实现,磁轴承极面位于两个不同半径的球形包络面上,如图1中红色虚线所示.由于球面磁极产生的电磁力始终经过磁极球心,当磁极球心与转子质心重合时,无论转子在磁间隙内处于什么位置,都不会产生扭转力矩,从而实现了平动自由度对径向转动自由度的解耦.因此,转子径向偏转只受力矩器控制.

MSCSG 采用LFMB 为力矩器驱动转子偏转,LFMB产生的电磁力依据安培力定律,即磁感应强度为B的磁场中沿与磁场垂直方向放置长度为L的线圈,当流经线圈中电流为I 时,线圈将受到大小为BIL的安培力作用.LFMB组件结构如图2所示,转子外沿一周的狭长内壁上放置着上、下两层磁钢,两层磁钢的内、外磁钢间充磁方向相反,因此形成了图2中虚线所示的闭合磁场.LFMB的定子部分由四组匝数相同的线圈构成,位于内外磁钢间的狭缝中,沿LFMB周向均匀分布,四组线圈成对使用,正对的两组线圈为一对,用于实现转子的二自由度偏转控制.

图2 LFMB工作原理图Fig.2 Working principle diagram of LFMB

以LFMB 几何中心o 为原点定义定子坐标系o–xyz,其中x轴与y轴分别与相对方向两组线圈中心线重合,z轴方向根据右手定则确定.当与磁场垂直方向放置的线圈通入电流时,线圈的上下两部分将分别产生垂直于线圈及磁场方向的安培力,合力大小为式中n为线圈匝数.当相对方向线圈通入大小相等、方向相反的电流时,磁轴承将尝试大小相反、方向相反的的安培力,形成力偶驱动转子径向偏转.根据图2中LFMB工作原理图,并结合式(1)中电流与安培力间的线性关系可知,沿x,y方向的偏转力矩px,py表达式为

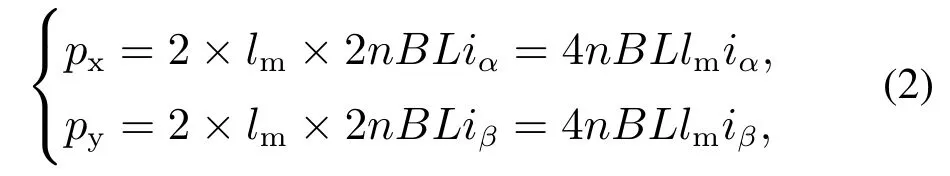
式中:iα,iβ分别为线圈中驱动转子绕x,y轴偏转的控制电流,lm为LFMB定子半径.

高速旋转的MSCSG转子,其径向偏转两自由度满足陀螺技术方程[5]:

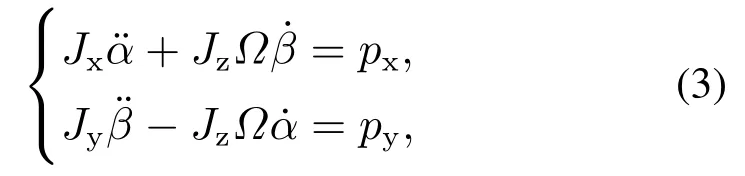
式中: Jx,Jy为转子相对于x轴及y轴的转动惯量,大小与转子赤道转动惯量Jr相等;Jz为转子相对于z轴的转动惯量;Ω 为转子轴向角速度,满足Ω2πFr,Fr为以频率为单位的轴向角速度;α,β分别为传感器测得的转子绕径向x,y轴偏转角度.

3 MSCSG 转子偏转控制器设计及数字化实现

3.1 分散PID结合滤波交叉反馈的转子偏转控制律

LFMB对MSCSG转子径向偏转通道的控制过程如图3所示,控制通道主要包括传感器、抗混叠滤波器、控制器、功率放大器.图3的闭合回路中,抗混叠滤波器将传感器采集到的转子偏转角信息α,β进行降噪处理后传递至控制器,控制器根据偏转指令信息αr,βr以及当前转子偏转角信息确定偏转指令,功率放大器将偏转指令对应的电压信号转化为控制电流,从而驱动LFMB对转子产生二自由度控制力矩.

图3 转子偏转控制系统框图Fig.3 Block diagram of rotor tilt control system

根据图3中的转子偏转控制系统框图可知,偏转通道的控制电流表达式为

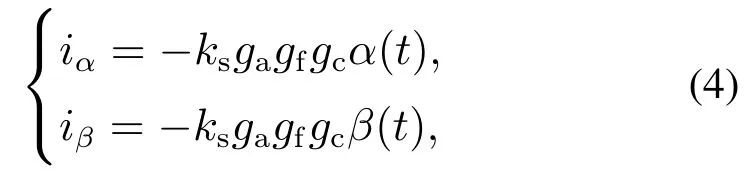
式中:ks为传感器比例增益;gf,gc,ga分别为抗混叠滤波器、控制器、功率放大器的输入–输出传递函数变换算子,对其进行拉普拉斯变换L满足关系式L[gf

PID控制器是最常用的控制器,具有结构简单、可靠性高、易于实现的优点,在转子低转速运行条件下应用范围最广[16].但是PID控制器存在相位滞后的问题,随转子转速升高,径向偏转通道的陀螺效应增强,由转速引起的系统状态变化给转子偏转控制增加了难度.尽管在理论上通过频繁调节PID控制器的积分系数和微分系数可以使涡动模态(包括进动和章动)下的相位滞后情况得到改善,但是在工程实践过程中,这种调节方式将引入更多的噪声,不具备现实可操作性.因此,为抑制陀螺效应,必须对高转速条件下控制器的滞后相位进行补偿.

滤波交叉反馈是改善控制器相位滞后的有效方法[17].为此,本文采用基于分散PID的滤波交叉反馈控制律,其中:PID控制器为基本的控制器,通过二阶低通滤波器将转子径向偏转角信号中的进动频率分量提取,同时通过二阶高通滤波器将偏转角信号中的章动频率分量提取,根据低通系数和高通系数所占比例的不同决定对两种涡动信号控制程度的强弱;此外,考虑到低转速条件下陀螺效应不明显,因此令交叉信号与转速信号相乘,从而在低转速条件下低陀螺效应不明显时,减弱交叉控制量,使PID控制器起主要作用;随着转速的升高,交叉控制量的比重不断增大,从而实现对进动和章动的有效抑制控制.MSCSG转子偏转通道采用的分散PID结合滤波交叉反馈控制律对应的等效控制框图如图4所示.图中: ga(s)为功率放大器传递函数,gf(s)为抗混叠滤波器传递函数,ks为传感器比例增益,gb(s)为分散PID控制器传递函数,kl为低通系数,kh为高通系数,wp(s)为用于抑制进动的低通滤波器传递函数,wn(s)为用于抑制章动的高通滤波器传递函数,高、低通滤波器的表达式分别为

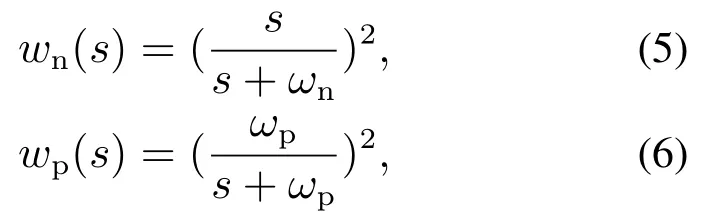
式中ωn,ωp分别为高通、低通截止频率.

因此,根据式(2)–(4)以及图4所示的控制框图可知,闭环MSCSG转子系统中偏转通道的动力学方程组为

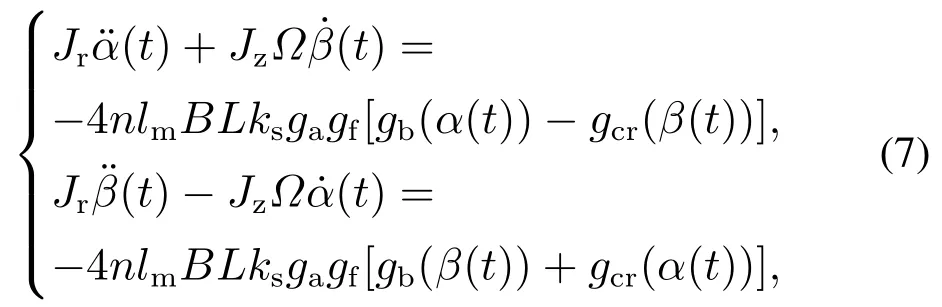
其中滤波交叉反馈算子gcr对应的传递函数表达式满足关系式:

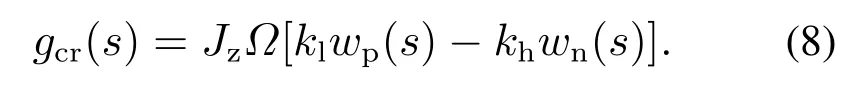
图4 基于分散PID结合滤波交叉反馈的控制器等效框图Fig.4 Equivalent diagram for controller based on decentralized PID plus filter cross feedback

3.2 转子偏转控制器数字化实现

第2.1节中的控制器是在s域中进行设计的.该控制器的实现方式分为两种,一种是通过s域的模拟控制器实现,一种是通过z域的数字控制器实现.模拟控制器线路结构简单,但是不灵活、不稳定.对于MSCSG转子控制系统,开发调试过程中调整控制器参数在所难免,如果采用模拟控制器,需要采用多种阻值、容值的电阻、电感,并通过电子开关的选通才能将控制器参数修改.随着近年来数字信号处理技术的发展,数字控制器为解决控制器灵活性差的问题提供了途径.数字信号处理器(digital signal processor,DSP)是目前使用最普遍的数字控制器,配备有高速数据采集功能和多指令处理功能,将高速运算能力与微机操作系统结合在一起,运算速度远高于普通计算机.考虑到DSP对外接设备配置要求较为严格,影响了配置的灵活性,本文利用现场可编程门阵列(field programmable gate array,FPGA)芯片I/O资源丰富与DSP运算能力强的优势,采用基于DSP+FPGA的数字控制系统对MSCSG转子偏转通道进行稳定控制,该方案具有功耗低、集成度高、体积和重量小的优势.基于DSP+FPGA的数字控制系统功能流程图如图5所示,DSP的AD单元和CAP单元对电流信号、位移信号和转速信号进行检测,DSP根据位移信号和转速信号给出控制量后传递至FPGA,FPGA模块根据控制指令产生各控制通道功放端所需的控制电压,从而实现对高速MSCSG转子的稳定控制.

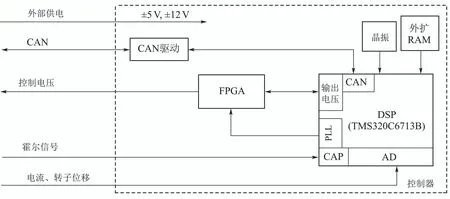
图5 基于DSP+FPGA的数字控制系统功能流程图Fig.5 Function flowchart for digital control system based on DSP+FPGA

图4中的控制算法数字化实现的过程中,主要在DSP中进行程序编写.本文采用双线性变换法,将s域的控制器传递函数转化至z 域进行离散化处理,随后根据离散化的传递函数推导数字控制程序中的差分方程.对于PID控制器,传递函数表达式为

其中kp,ki,kd分别为比例、积分、微分系数.

采用双线性变换法条件下,s域到z域的映射函数为

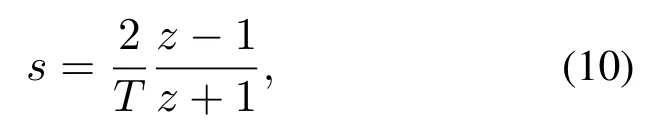
式中T为采样时间.将式(10)代入式(9),得传递函数z域表达式:

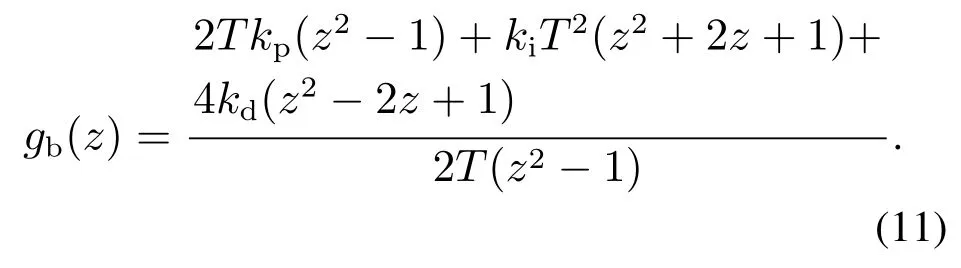
将式(11)中分子、分母同时除以z2,得

为将z域传递函数转换为差分方程,先将式(12)进行等效转换,得

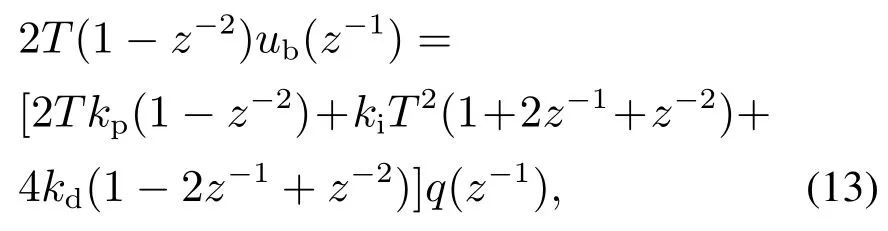
式中:q(z−1)为控制器输入量;ub(z−1)为PID控制器产生的控制量,进而可推导分散PID控制程序中的差分方程表达式为

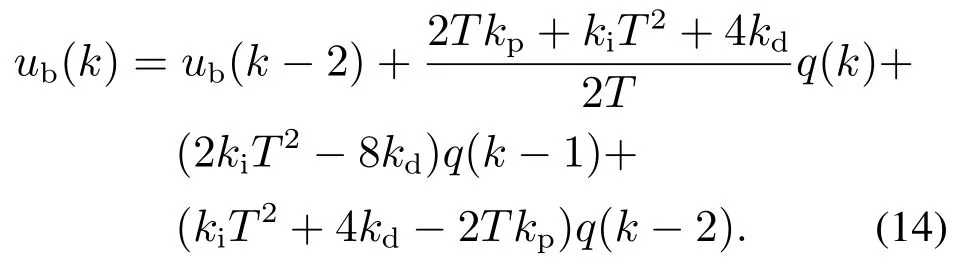
同理,可确定高通滤波器、低通滤波器控制程序中的差分方程表达式分别为

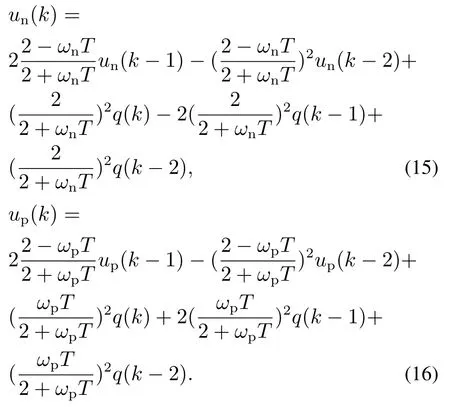
结合图4以及式(14)–(16)可确定基于分散PID 结合滤波交叉反馈的数字控制算法.

4 控制器稳定性分析

本文通过转速跟轨迹曲线观察本文所提出的基于分散PID结合滤波交叉反馈控制器对转子系统稳定性的影响,并通过单纯PID控制条件下的转速根轨迹曲线与其进行对比.转速根轨迹曲线都是通过MATLAB仿真实现,使用的转子控制系统主要参数如表1所示.其中:ka为功放增益,ωa为功放截止频率,ωf为抗混叠滤波器截止频率.曲线绘制过程中,采用循环指令对转速赋值,在0∼170 Hz范围内,以0 Hz为起始转速,转速间隔为5 Hz,通过pzmap函数计算系统的极点,并将虚轴附近的极点以描点的方式画出,从而得到图6所示的转子系统主导转速根轨迹曲线.由图6(a)可知,采用PID控制器时,起始转速条件下,系统的极点位于虚轴左侧,系统稳定;随转速升高,极点位置发生变化,当转速由45 Hz升至50 Hz时,极点轨迹首次从左半平面穿过虚轴进入右半平面,系统出现不稳定极点;转速由150 Hz升至155 Hz时,极点全部位于右半平面.因此转子系统在转速为0∼45 Hz时,极点位于左半平面,系统稳定;在转速大于50 Hz时,右半平面存在极点,系统不稳定.由图6(b)可知,采用分散PID结合交叉滤波反馈控制器时,起始转速条件下,系统的极点位于虚轴左侧,系统稳定;随转速升高,极点向虚轴靠近,当转速由105 Hz升至110 Hz时,极点轨迹从左半平面穿过虚轴进入右半平面,系统出现不稳定极点.因此转子系统在转速为0∼105 Hz时,极点位于左半平面,系统稳定;在转速大于110 Hz时,右半平面存在极点,系统不稳定.转速根轨迹对比结果表明,在所提出的控制方法作用下,陀螺效应对转子系统稳定性造成的影响得到了有效抑制,转子的转速稳定区间得到了拓展.

5 转子偏转稳定控制实验

为验证本文所提出的控制方案对MSCSG转子偏转系统的稳定控制效果,本文采用DSP+FPGA为核心的数字控制系统,以LFMB支撑的MSCSG转子为被控对象,在转子升转速过程中对转子径向两偏转通道进行稳定性验证.MSCSG试验系统如图7所示,主要由电源、示波器、上位机、控制板、功放板和MSCSG原理样机构成.数字控制算法以5 MHz频率在DSP中高速运行,上位机可以实现对控制器参数的实时设置、显示.

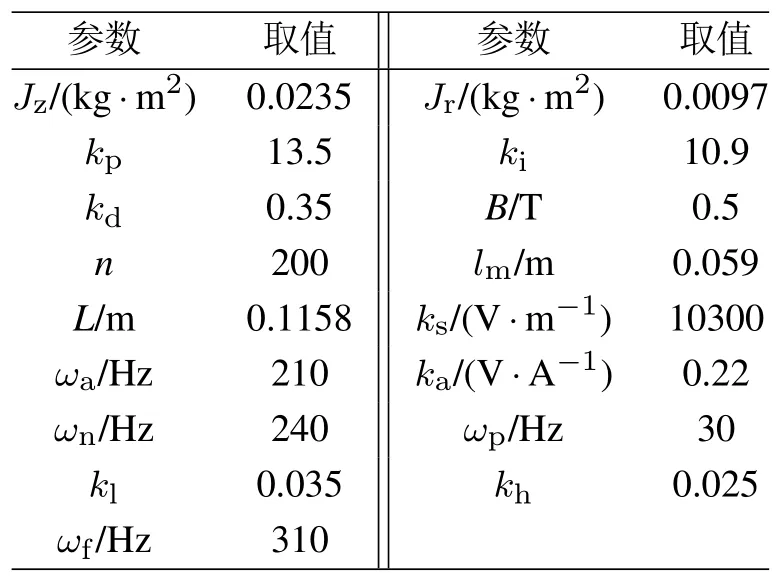
表1 转子系统参数Table 1 Parameters of rotor system

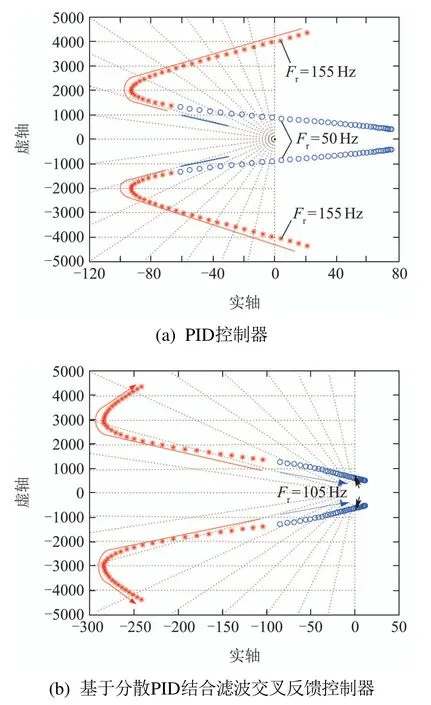
图6 根轨迹图Fig.6 Root locus diagram

为验证所提出稳定控制方法的有效性,本文在升速实验过程中分别采用单纯的PID控制以及所提出的分散PID结合滤波交叉反馈数字控制方法进行对比实验.实验过程中转子从静止状态的Fr0 Hz开始升速,同时用示波器实时显示检测到的偏转角α和β对应的电压信息.偏转角信息中,纵轴代表电压,每格代表200 mV.根据MSCSG设计指标,转子偏转角的振动幅值超过400 mV时,转子系统失稳.

图7 MSCSG试验系统Fig.7 Experimental setup of MSCSG system

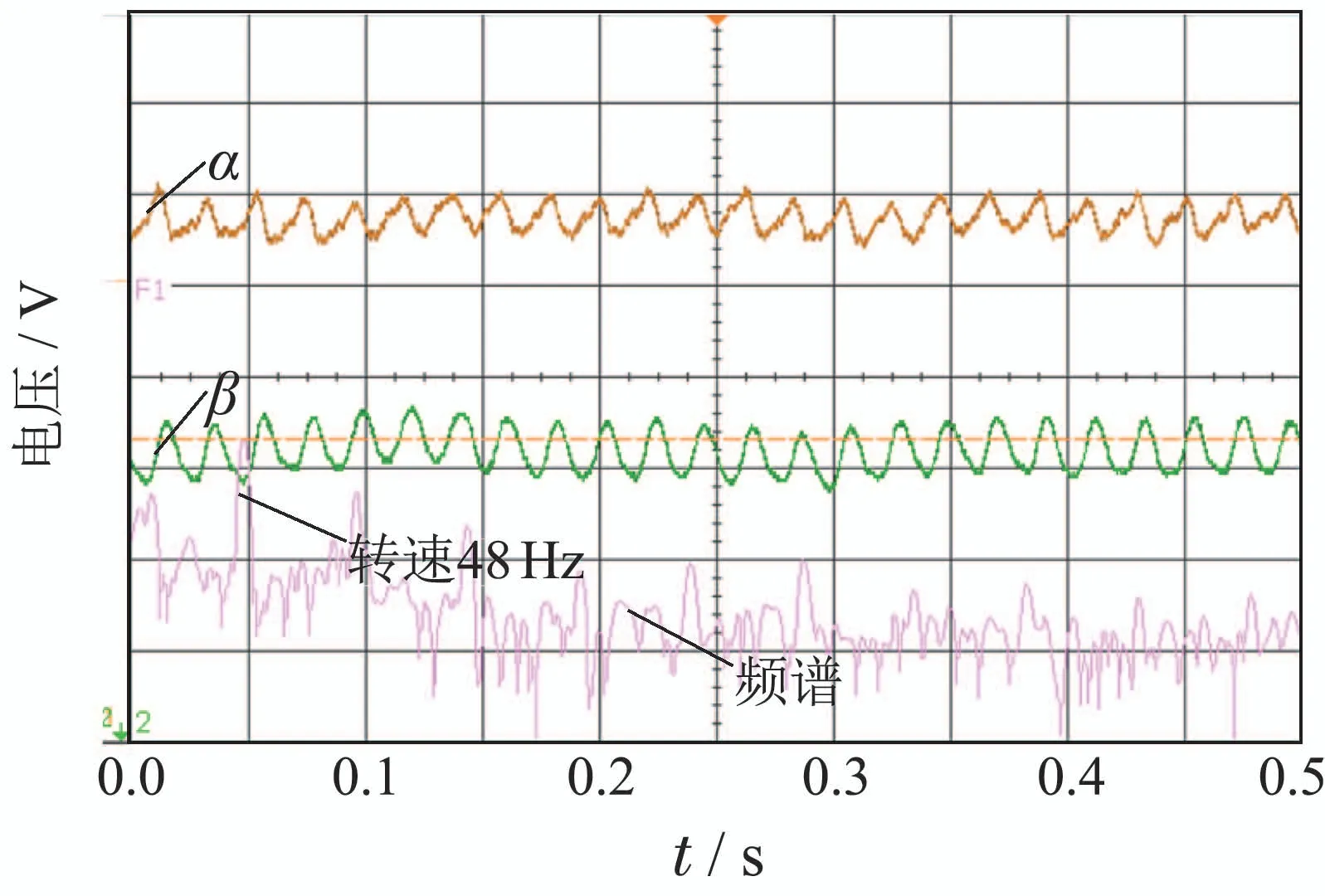
图8 48 Hz条件下单纯PID控制实验结果Fig.8 Experimental result with single PID control at 48 Hz

采用单纯PID 控制方法条件下,转子转速升至48 Hz时,偏转角响应曲线如图8所示.由图8可知,转速为48 Hz 条件下,转子偏转角变化的峰峰值约为0.17 V,不存在较大范围的波动,转子偏转系统稳定.当转速继续上升,采用单纯PID控制方法条件下,转速升至3200 r/min(约53 Hz)时,偏转角响应曲线和李萨育图分别如图9(a)和图10(a)所示.其中李萨育图是通过偏转角α和β合成的二维图.此外,利用示波器中Math模块的FFT功能,对采集到的α通道信号进行频域分析,并将该通道的频谱信息在示波器中与其对应的偏转角响应信息一并显示.频谱信息中,纵轴代表幅度,横轴代表频率,每横格代表50 Hz.图9(a)中,α和β对应的电压信号均出现大范围的波动,偏转角变化的峰峰值达到近1 V,且其频谱中,转速同频量不再是最主要的成分,频率为2.1 Hz的进动分量幅度最大;根据图10(a)中的李萨育图可知,转子转速为53 Hz 时,偏转角的中心轨迹变化范围远超出400 mV的稳定区间,且偏转角呈继续发散的趋势.综合转子偏转通道的时域图、频谱图、李萨育图可知,采用分散PID控制条件下,MSCSG转子系统在转子转速升至53 Hz时不稳定.

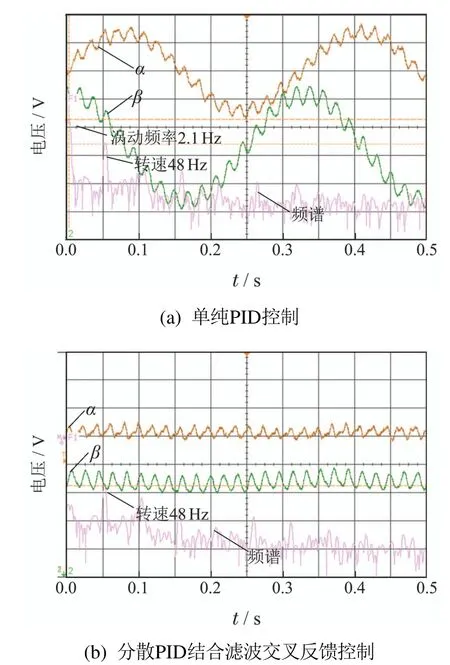
图9 53 Hz条件下转子偏转角响应曲线及频谱图Fig.9 Tilt angle and frequency spectrum responses of the rotor at 53 Hz

转子在转速为53 Hz时,采用分散PID结合滤波交叉反馈数字控制方法条件下,转子偏转通道的偏转角响应以及李萨育图分别如图9(b)和图10(b)所示.由图9(b)可以看出,转子转速升至53 Hz时,α与β对应的电压信号均值分别为1.4763 V,1.4944 V,偏转角变化的峰峰值为0.18 V,不存在大范围的波动,且其频谱图中,转速同频量的幅值最大;根据图10(b)中的李萨育图可知,转子转速为53 Hz时,偏转角的中心轨迹变化范围始终小于200 mV.综合转子偏转响应的时域图、频谱图、李萨育图可知,采用所提出控制方法时,MSCSG转子系统在转子转速为53 Hz条件下稳定.对比图9(a)和图10(a)中采用单纯PID控制条件下转速同样为53 Hz时的实验结果可知,基于分散PID结合滤波交叉反馈的MSCSG转子偏转控制器有效地抑制了陀螺效应,克服了进动对转子系统稳定性的影响.

在转子转速为53 Hz保持稳定旋转,克服了陀螺效应的基础上,继续对MSCSG转子升速,直至满足额定转速指标5000 r/min(约84 Hz)为止.转子转速频率为84 Hz条件下,转子偏转角响应曲线和李萨育图分别如图11和图12所示.由图11可以看出,转子转速升至84 Hz 时,α 和β 对应的电压信号均值分别为1.4765 V,1.4862 V,偏转角变化的峰峰值为0.19 V,不存在大范围的波动,且其频谱图中,转速同频量的幅值最大;根据图12中的李萨育图可知,转子转速为84 Hz 时,偏转角的中心轨迹变化范围始终小于400 mV,保持在稳定区域内偏转.

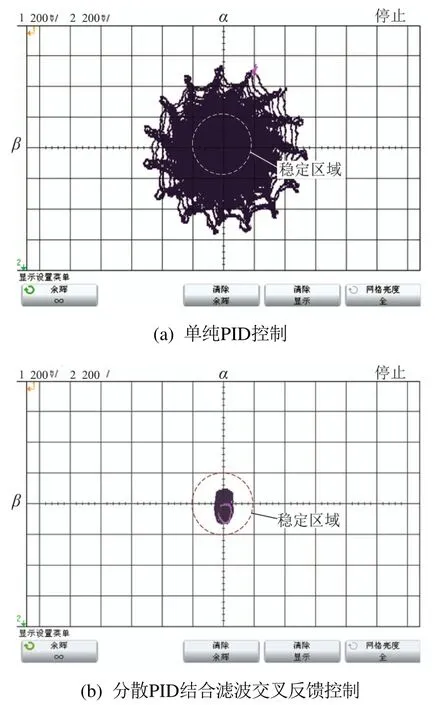
图10 53 Hz条件下转子李萨育图Fig.10 Lissajous figure of rotor at 53 Hz

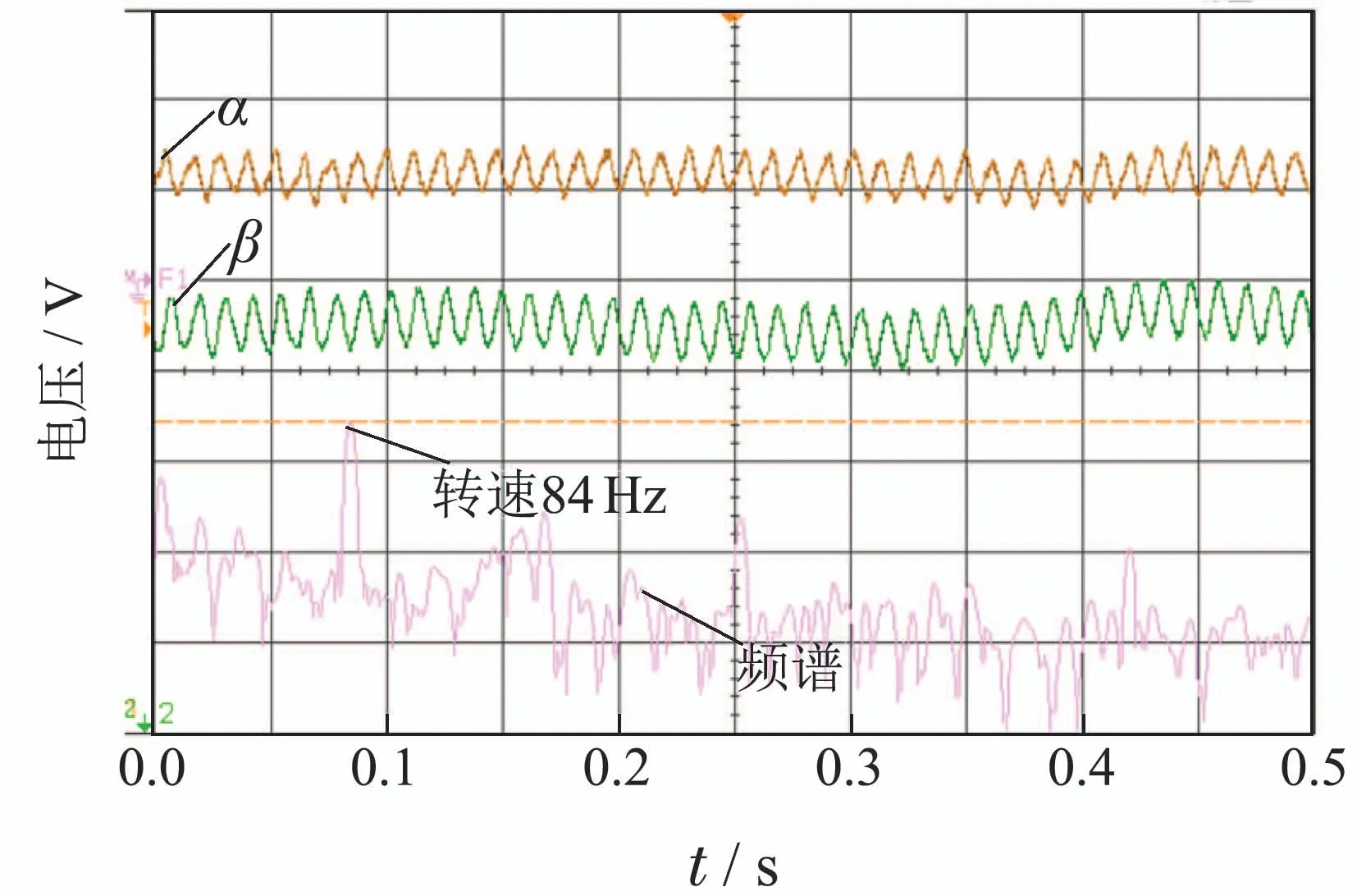
图11 84 Hz条件下转子偏转角响应曲线及频谱图Fig.11 Tilt angle and frequency spectrum responses of the rotor at 84 Hz

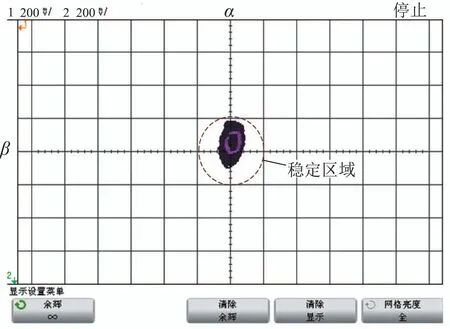
图12 84 Hz条件下转子径向李萨育图Fig.12 Lissajous figure of rotor at 84 Hz

综合转子偏转响应的时域图、频谱图、李萨育图可知,MSCSG转子系统在转子转速为84 Hz条件下依然可以保持稳定悬浮,实现了高转速条件下稳定控制的目标.

6 结论

本文针对强陀螺效应影响MSCSG转子偏转系统稳定性的问题,提出采用分散PID结合滤波交叉反馈控制方法,并通过DSP+FPGA为核心的数字控制器实现对MSCSG转子的稳定控制.仿真和实验结果表明,所提出稳定控制方法实现了对高速MSCSG转子强陀螺效应的有效抑制,在该方法作用下,转子偏转通道可以在0∼5000 r/min 转速范围内稳定运行,为MSCSG实现检控一体的功能提供了重要保证.为推动MSCSG早日走向航天应用,下一步将开展载体航天器空间机动条件下MSCSG转子偏转通道稳定控制研究.