整流罩头部钝度比对运载火箭气动性能影响研究
闫指江,吴彦森,宫宇昆,张耘隆,秦 曈
(北京宇航系统工程研究所,北京,100076)
0 引 言
近些年,中国的火箭设计及制造技术飞速发展,特别是以CZ-6、CZ-7和CZ-5为代表的新型运载火箭相继成功首飞和应用发射,使中国运载火箭综合能力进入国际先进行列[1]。而火箭的外形设计是其中的重要组成部分,直接影响了火箭的弹道特性、结构静动力特性以及火箭的飞行稳定性等[2]。而外形设计中整流罩的外形设计是其中的关键环节,不但直接影响了内部的有效载荷尺寸,而且还决定了全箭的气动特性及相应的气动热环境等。需要优化其几何参数,设计出具有良好气动性能和外形包络的整流罩外形。
根据模线设计理论,飞行器的气动外形主要由纵向母线线型和各控制站位横截面形状确定[3],整流罩的外形一般由“斜锥+柱段+倒锥”的组成,而柱段和倒锥对气动特性的影响相对较小,因此火箭整流罩前锥母线的线型不仅直接决定了整流罩局部的气动性能,而且也会对全箭的气动性能产生较大的影响。
本文在前期火箭外形设计及优化工作的基础上只改变整流罩前锥曲线的外形,对5种钝度比的冯·卡门整流罩母线线型的运载火箭全箭气动特性、局部气动载荷和气动加热性能进行对比分析。
1 母线线型
在坐标R-X下,X轴沿箭体对称轴且指向箭体底部,冯·卡门曲线的线型方程可以写为
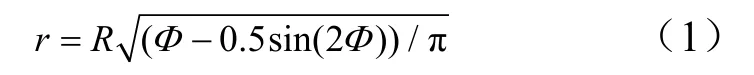

由于钝度比不同,曲线的长度也不相同,为了使得母线线型的对运载火箭气动性能的影响更具有可比性,选取 5种冯卡门曲线线型具有相同的最大半径,且采用相同半径的球头对5条曲线进行前缘的钝化处理。图1给出了前缘钝化后的5条曲线。
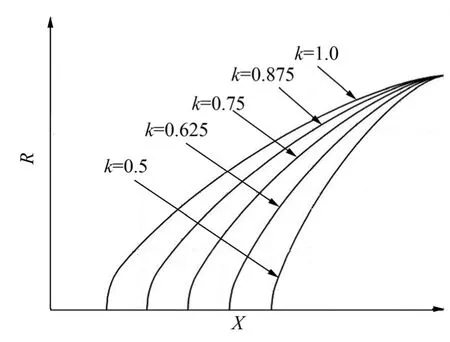
图1 5种冯·卡门曲线对比Fig.1 Comрarison of Five Kinds of Van Karman Line
2 全箭气动特性影响分析
开展捆绑4个助推器火箭的全箭气动特性计算,整流罩钝度比k=1的实体模型如图2所示。
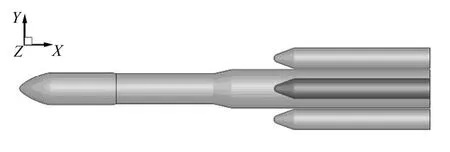
图2 k=1的实体模型Fig.2 The Solid Model of k=1
本文采用了精度较高的数值计算方法进行全箭气动特性的计算,计算网格采用结构化网格,为了保证计算结果对比更为准确,只改变整流罩前锥的网格点,全箭其余位置的网格点位置不变,k=1的冯·卡门曲线线型的整流罩网格模型如图3所示。

图3 k=1的整流罩网格模型Fig.3 The Grid Model of Fairing of k=1
采用有限体积方法求解三维坐标系下的Navier-Stokes方程进行计算,采用RANS计算方法[4]。选用基于密度的耦合求解器进行计算,湍流模型选用S-A模型,选用Roe-FDS算法进行计算[5]。
全箭轴向力系数对比如图4所示。由图4可知,不同的整流罩冯卡门斜锥对全箭的气动特性产生一定的影响,但未改变随Ma数变化的整体气动特性规律。
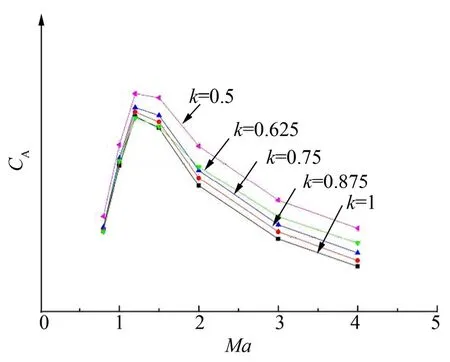
图4 全箭轴向力系数对比Fig.4 Comрarison of Axial Force Coefficients of the Whole Launch Vehicle
从图4可以看出随着钝度比k值的减小,全箭轴向力系数在超声速段逐渐增加,相比k=1构型的轴向力系数,k=0.5构型的轴向力系数增加约25%。在亚跨声速段全箭轴向力系数变化较小。
图5为全箭法向力系数对比。从图5可以看出随着钝度比k值的减小,全箭的长度在逐渐减小,因此全箭法向力系数也略有减小。在亚跨声速段,相比k=1构型的轴向力系数,k=0.5构型的法向力系数减小约1%,在超声速段,减小约4%。

图5 全箭法向力系数对比Fig.5 Comрarison of Vertical Force Coefficients of the Whole Launch Vehicle
图6为全箭压心系数对比。从图6可以看出随着钝度比k值的减小,在亚跨声速段压心系数逐渐减小,在Ma>2时,随着k值的减小,压心系数逐渐增加。

图6 全箭压心系数对比Fig.6 Comрarison of the Centre of Pressure Coefficients of the Whole Launch Vehicle
3 整流罩气动载荷影响分析
3.1 整流罩整体受力影响分析
提取 5种不同冯·卡门前锥的运载火箭整流罩受到的轴向力系数和法向力系数对比,见图7和图8。
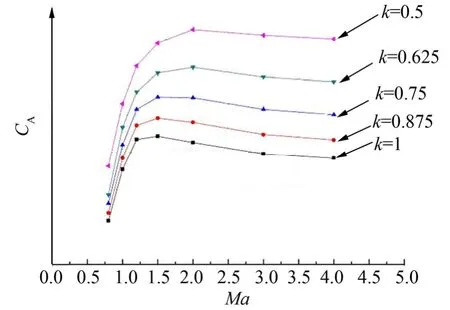
图7 整流罩轴向力系数对比Fig.7 Comрarison of Axial Force Coefficients of the Fairing

图8 整流罩法向力系数对比Fig.8 Comрarison of Vertical Force Coefficients of the Fairing
从图7可以看出随着钝度比k值的逐渐减小,整流罩所受到的轴向力逐渐增加,钝度比由k=1减小到k=0.5时,轴向力系数将增加约1倍。
从图8可以看出随着钝度比k值的逐渐减小,法向力系数逐渐减小,且钝度比由k=1减小到k=0.5时,法向力系数在亚跨声速段减小约 10%,在超声速段减小约20%。
钝度比的变化会显著改变整流罩局部的受力情况,这样的变化将会影响全箭的载荷设计。
3.2 整流罩局部静气动载荷影响分析
对全箭数值计算结果进行分站积分,提取整流罩的轴向分布载荷和法向分布载荷,如图9、图10所示。
由图9可知,随着整流罩钝度比k值的逐渐减小,整流罩前锥的轴向分布载荷峰值显著增大,但前锥的轴向分布载荷的变化对柱段和倒锥段的影响较小。
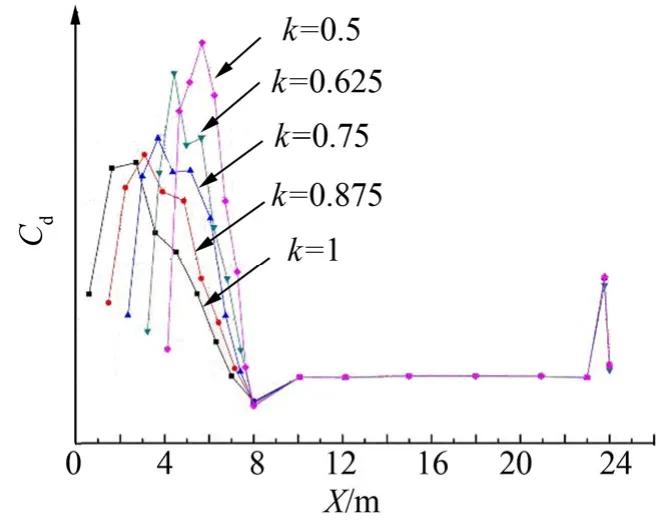
图9 整流罩轴向分布载荷对比Fig.9 Comрarison of Axial Distribution of Load of Fairing
由图10可知,随着整流罩钝度比k值的逐渐减小,整流罩前锥单位长度剖面的法向力系数变化不大,但整流罩柱段的单位长度剖面的法向力系数逐渐增加。

图10 整流罩法向分布载荷对比Fig.10 Comрarison of Vertical Distribution of Load of Fairing
若整流罩钝度比由1减小为0.75,将会导致整流罩前锥局部轴向分布载荷峰值增加约15%,且整流罩柱段的单位长度剖面的法向力系数最大值将增加20%,由此产生的影响是整流罩在设计中需要局部加强。
3.3 整流罩局部动载荷影响分析
整流罩局部动载荷的影响通过肩部脉动压力变化来评估[6],即采用肩部脉动压力峰值与影响区域面积的乘积来判断。若模型直径相同,则脉动压力强度等于脉动压力峰值和在模型上的影响距离的乘积[7]。
两型整流罩钝度比分别为1.2和1.0的火箭,其中钝度比小的火箭α=6°状态下,整流罩锥柱交界面 A剖面(如图11所示)合成脉动压力系数为1,其脉动压力作用范围为9;钝度比大的火箭α=6°状态下,整流罩锥柱交界面A剖面合成脉动压力系数为0.9697,其脉动压力作用范围为8,若假设两型火箭开展脉动压力风洞试验采用同样整流罩直径的模型,则脉动压力强度比为1.0773。

图11 整流罩锥柱交界面A剖面Fig.11 Section A of the Interface Вetween the Cone and Column of the Fairing
若两个风洞试验模型整流罩直径相同,则钝度比小的火箭脉动压力强度增加 7.73%,考虑小范围内脉动压力强度线型增加的原则,若整流罩钝度比由 1.0减小为0.75,则肩部脉动压力增加约10%。
4 整流罩气动加热影响分析
对于整流罩端头的驻点热流,采用层流的后掠圆柱理论计算[8];斜锥的典型位置热流采用层流锥面热流工程计算方法进行计算[9]。
初始温度为303 K,计算时不考虑截面间的横向传热,略去太阳对壳体辐射加热及舱内空气自然对流传热。分别针对驻点、球头和前锥切点、切点和驻点的中间点等典型位置展开计算,典型计算位置如图12所示。

图12 气动加热计算典型位置示意Fig.12 Schematic Diagram of Tyрical Positions for Aerodynamic Heating Calculation
图13和图14分别为第3计算点和第4计算点的冷壁热流值,可以看出随着钝度比k值的不断减小,前锥段不同位置处由气动加热所产生的冷壁热流均逐渐增加,当钝度比小于 0.75,峰值热流变化较小。钝度比若由1减小为0.75,则前锥段的冷壁热流峰值增加约10%,总加热量增加约10%。

图13 第3计算点的冷壁热流曲线Fig.13 The Cold Wall Heating Flux Diagram of the Third Calculated Point
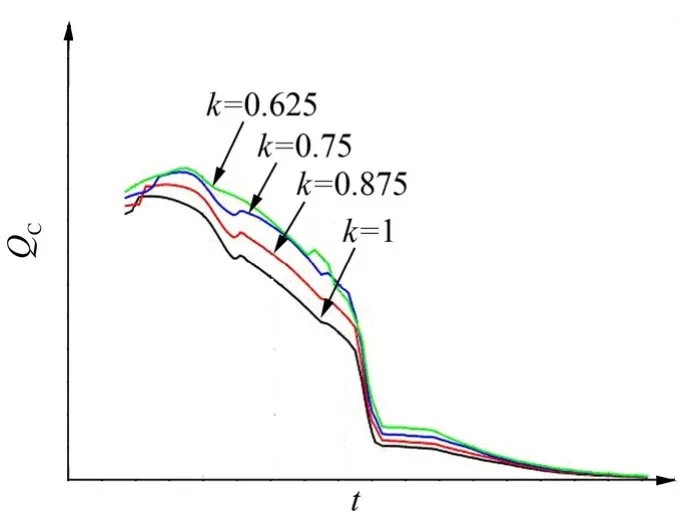
图14 第4计算点的冷壁热流曲线Fig.14 The Cold Wall Heating Flux Diagram of the Fourth Calculated Point
5 结 论
本文开展了整流罩钝度比对运载火箭性能影响研究,对5种冯·卡门曲线线型的运载火箭全箭气动特性、气动载荷和整流罩气动加热进行了影响分析,从分析结果可以看出:
a)整流罩钝度比k=1对全箭气动特性、整流罩局部气动载荷以及气动加热均有利。不但全箭的阻力最小,而且整流罩受到的气动载荷和气动加热也最小。
b)随着钝度比减小,全箭轴向力系数逐渐增加并且增速变快,这将导致全箭阻力大幅增加,而全箭法向力系数和压心系数变化不大。
c)随着钝度比减小,整流罩的局部静载荷和动载荷均有所增加,若钝度比减小为 0.75,则轴向分布载荷峰值增加约15%,法向分布载荷峰值增加20%,肩部脉动压力强度增加 10%,这样的变化会对全箭的载荷设计产生一定的影响。
d)随着钝度比减小,整流罩前锥段的冷壁热流和总加热量均会增加,若钝度比减小为 0.75,则冷壁热流峰值和总加热量均增加约10%,需考虑加强防热。

