功能性点阵结构设计优化技术研究

朱健峰，戴 宁，刘乐乐

(南京航空航天大学机电学院，江苏 南京 210016)

自然界充满了各种天然多孔结构，如骨骼、蜂窝、竹子纤维等[1-2]，这些功能性多孔结构能够让自然界的生物具有适应不同生活环境的能力。研究人员从这些生物多孔结构中获得灵感，将点阵结构应用到不同的实物中实现轻量化设计以及性能优化，如网格状的桁架桥、蜂巢状建筑、仿生多孔骨组织以及采用多孔填充的金属零部件等，促进了点阵结构的发展。点阵结构作为极具潜力的先进轻质功能结构，与传统结构相比具有很多特有的优异性能[3]，在很多领域特别是航空航天领域具有巨大的应用潜力[4]。近些年增材制造[5]的发展为点阵结构的制造和应用提供了极大的便利，设计者在产品开发设计阶段不受刀具加工以及专用模具等加工条件方面的限制[6]，可以直接、快速地把设计想法变为实体零件，大大拓宽了设计者的设计思路。

通过对点阵结构的合理设计与选用，可以实现对目标模型的最佳轻量化，并在轻量化的同时维持或增强原始模型的特定力学特性，实现目标模型的特异性功能。本文将拓扑优化与实体几何构造法相结合，进行点阵结构的参数化设计和性能预测，针对性地实现零件的功能性轻量化设计[7]。

1 点阵结构设计

点阵结构是一种模拟生物微观分子构型，通过连接杆件单元和节点，并按照一定的规律排列组成的一种具有周期性的拓扑结构，不同的点阵结构单元构成的轻质点阵结构具有不同的力学性能[8]。现有的点阵结构类型繁多，实际应用过程中难以在相应的载荷条件下确定对应的点阵结构，设计时选择困难。本文提出了基于拓扑优化原理的点阵结构设计方法，在不同载荷、边界条件下得到对应的优化点阵单元结构，实现功能性点阵力学性能匹配。

1)基于拓扑优化的点阵结构单元。

拓扑优化是一种数学优化方法，其本质上是在不断迭代分析的过程中寻找设计区域内最优的材料分布。本文采用基于变密度法的拓扑优化算法[9]进行微结构单元的拓扑优化设计。变密度法[10]是最常用的拓扑优化方法，其建立了材料弹性模量与材料密度之间确定的数学关系，每个设计区域内网格单元的密度为一个优化变量，密度阈值为0～1，它借鉴了均匀化方法的经验和成果，直接建立起设计材料的弹性模量与网格单元密度之间的线性关系。以单元刚度最大为优化目标，体积率20%作为约束条件，建立单元结构的拓扑优化模型：

find:x={x1,x2,…,xN}T∈RN

(1)

(2)

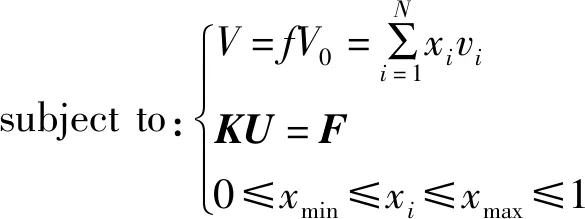
(3)

式中：x为整个优化模型的设计变量;xi为单元密度阈值；xmax,xmin分别为设计区域内网格单元相对密度的最大值和最小值；C(x)为整体结构(包含设计区域和非设计区域)的柔度矩阵；F为整体结构所承受的载荷矩阵；U为整体结构的位移矩阵；K为整体结构的刚度矩阵；ui为设计区域网格单元的位移矩阵；ki为设计区域单元的刚度矩阵；V为设计区域结构的有效体积；V0为设计区域的原始体积；vi为网格单元体积；f为设计区域内拓扑优化后结构相对于设计区域内原始结构的体积率；N为离散网格单元总数；P为惩罚因子。

设置如图1所示的4种载荷边界条件，分别代表立方单元承受拉压、扭转和剪切载荷时的4种情况。第一种为8个顶点受拉(压)载荷，6个面中心点固定约束，每个顶点均受到X,Y,Z轴3个方向的分力各5 N；第二种为8个顶点固定约束，6个面的中心点受拉(压)载荷，每个点均受到垂直于该面的拉(压)力20 N；第三种为顶面4个顶点各受5 N的集中力载荷，力的方向为逆时针方向，模拟扭转情况下的载荷条件，底面4个顶点固定约束；第四种为在原始立方体的右侧面上半部分与左侧面的下半部分分别施加5 MPa的面压力，模拟受剪切的载荷条件。

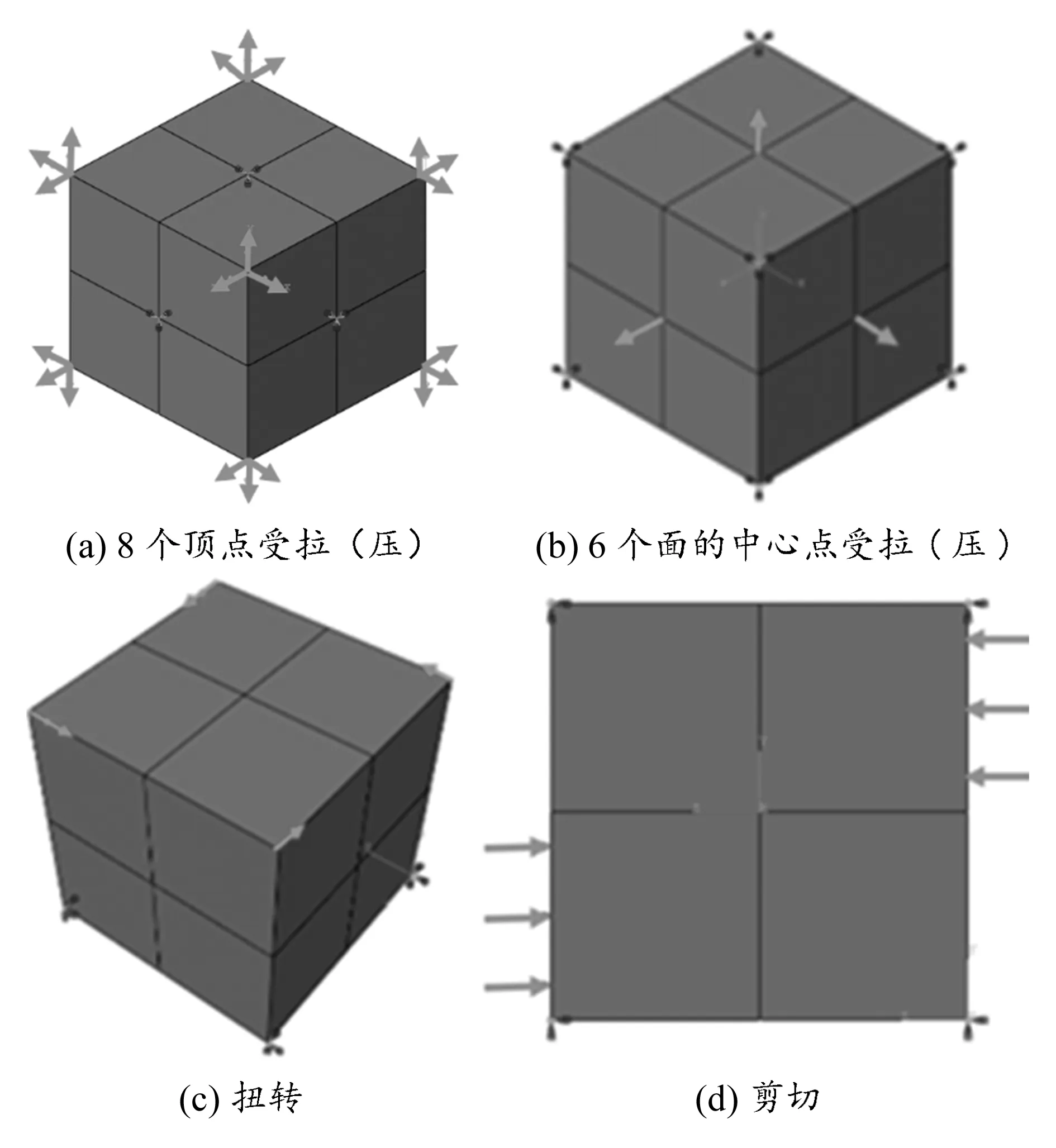
图1 4种载荷边界条件

前两种情况目标区域的载荷边界条件及模型具有三轴对称性，优化结果也具有对称特性；第三种情况模拟扭转载荷条件时各侧面受力方向一致，优化结果同样具有对称性；而在模拟剪切载荷条件时载荷边界只有一个方向，因此第四种拓扑优化模型不具有完全对称性。4种载荷边界条件下拓扑优化后的点阵结构单元如图2所示。结果充分体现了材料对于不同载荷工况的适应性。

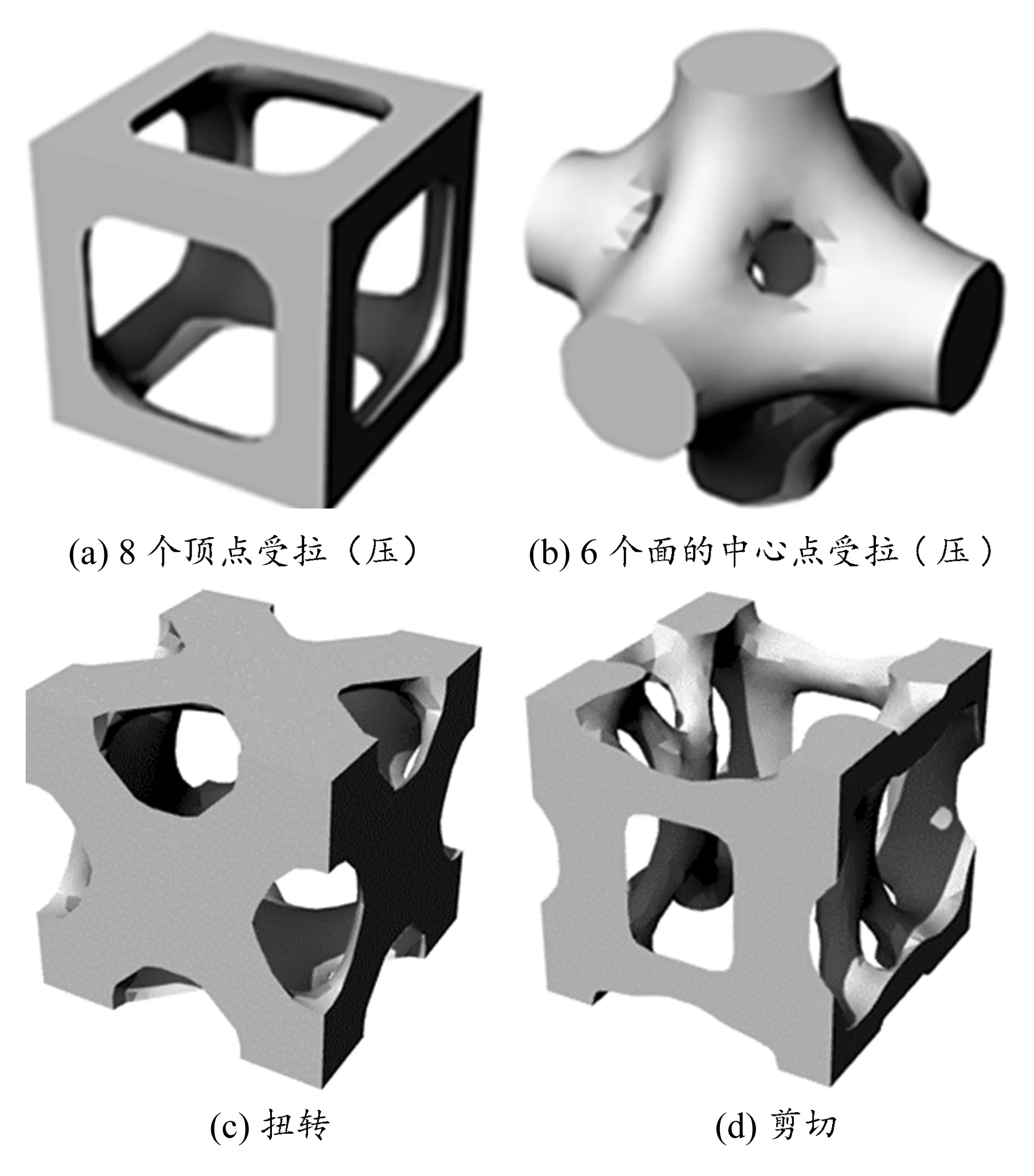
图2 4种载荷边界条件下的拓扑优化后点阵结构单元

2)拓扑点阵结构单元设计。

常见的三维点阵结构有面心立方、体心立方、八面体结构、金刚石结构、三维Kagome结构等[11]。拓扑优化直接获得的单元具有不规则形状，曲面复杂，不能直接用于对结构的轻量化设计，需要将拓扑优化获得的点阵结构单元规则化，形成具有规则形状的、具有一致特征的点阵结构规则单元，这一步本文称之为拓扑点阵结构单元的点阵化。

考虑到剪切载荷边界条件的不对称性，结合拓扑优化的结果，将4种载荷边界条件的拓扑优化单元分别设计为具有一致拓扑结构的规则点阵结构单元，如图3所示，并将这4种常见点阵结构单元作为拓扑优化的点阵化结果。

图3 拓扑模型的点阵结构

2 点阵结构单元力学性能模拟与实验

1)点阵结构单元力学数值分析。

采用均匀化理论对点阵结构单元进行分析，建立复合材料四阶刚度矩阵C[12]，共包含36个参数，由于四阶刚度矩阵的对称性以及所分析单元具有正交各向异性属性，因此36个未知参数可以减为9个独立未知参数。首先在点阵单元上分别施加6种载荷条件[13]，求出四阶刚度矩阵C中的未知参数，然后根据四阶刚度矩阵C求得其逆矩阵S:

(4)

式中：E1,E2,E3分别为点阵结构单元X,Y,Z3个方向的弹性模量；G12,G13,G23分别为点阵结构单元的剪切模量；ν12,ν21,ν13,ν31,ν23,ν32分别为点阵结构单元的泊松比。再计算出不同点阵结构轴方向的弹性模量、剪切模量和泊松比，并作出其与体积率的关系曲线图，如图4所示。

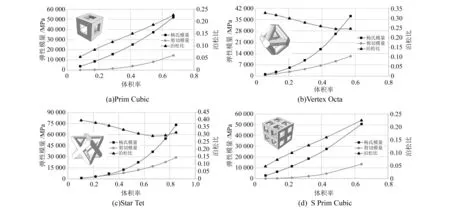
图4 4种点阵结构性能与体积率的关系曲线

2)点阵结构的准静态压缩性能实验。

采用准静态单向压缩实验来获得点阵结构的静力学性能。通过压缩实验(图5)获得点阵结构的力-位移曲线，再换算成名义应力-应变曲线，从而测得材料名义弹性模量E*。

图5 点阵结构压缩实验

点阵结构及标准拉伸试件采用选择性激光熔融技术(selective laser melting, SLM)制备。SLM技术能够制造复杂的点阵结构，可使用的金属粉末材料有钛合金、纯钛、不锈钢、钴铬铝合金、马氏体钢、铝合金、镍合金以及其他定制材料。实验选用316L不锈钢作为3D打印材料，其材料属性见表1。制作的实验试件外形尺寸为20 mm×20 mm×20 mm，每个试件在X,Y,Z方向均排列5层基本点阵单元，基本单元的尺寸为4 mm×4 mm×4 mm。改变点阵单元中杆件的半径，获得4种类型点阵单元5种不同体积率模型。在万能材料试验机(型号为cmt5305)上对试件分别施加初始接触力30 N，下压速度为1 mm/min，直至试件发生塑性变形，记录过程中试件的力-位移曲线。对曲线进行处理，换算成名义应力-应变曲线，并与数值模拟曲线进行对比，如图6所示。

表1 316L不锈钢材料属性

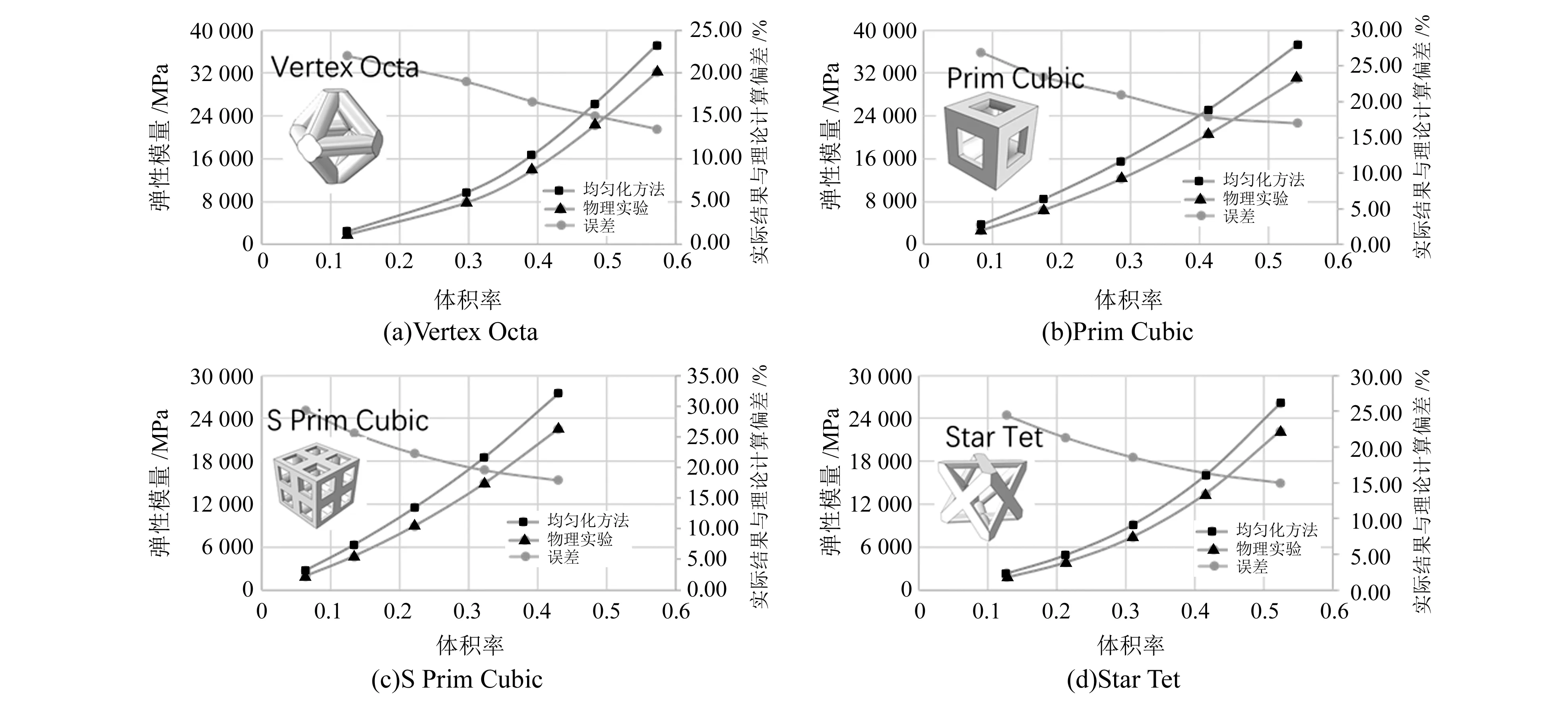
图6 316L不锈钢点阵结构弹性模量压缩实验与数值分析结果对比

由图可以看出，压缩实验得到的弹性模量与均匀化方法数值分析获得的结果的误差在35%以内，实验获得的弹性模量总是小于均匀化方法数值分析得到的结果。经过分析，误差主要是由于数值分析计算时采用的是理想模型，而实际的打印试验件存在缺陷。同时从图中也可以观察到，随着点阵结构体积率的增加，实验结果与数值分析结果之间的误差百分比越来越小，呈下降趋势，这说明随着杆径的增加，SLM工艺对点阵结构性能的影响逐渐减小。

3 点阵结构在连杆轻量化优化中的应用

以典型连杆结构为例对其进行受载情况下的有限元分析，点阵结构单元设为1 mm×1 mm×1 mm的正方体单元，材料选用钛合金Ti6Al4V，其弹性模量E为110 GPa，泊松比ν为 0. 33。将连杆模型导入到ABAQUS中，并进行有限元网格划分。

在顶部封闭的圆环中心设置一个参考点RP，将圆环内部表面与参考点设置耦合约束，如图7(a)所示。边界条件设置为底部开孔两端的螺栓孔固定约束，载荷条件为在参考点上施加垂直向上和向右的集中力各100 N，因为设置了耦合约束，集中力会均匀地分散在顶部圆孔的内表面，如图7(b)所示。

图7 连杆结构载荷边界条件

由图8(a) 所示的连杆Mises应力云图可以发现，最大应力集中在连杆与底部半圆环连接处的两侧，连杆中间部分应力偏低，可采用点阵结构填充，实现连杆结构的轻量化设计。由图8(b)所示的应变云图可以看出，整个连杆的变形主要是拉压应变，结合拓扑优化结果，选用与立方体中心拉压载荷下拓扑结果相似的Vertex Octa点阵单元对连杆结构进行填充，如图9所示。

图8 连杆优化前应力应变图

图9 Vertex Octa点阵单元填充结果

根据第2节中点阵结构性能分析的结果，当Vertex Octa点阵结构单元的体积率为0.295 776时，其弹性模量为9 762 MPa，泊松比为0.28。结合均匀化理论，在实验中以此均质材料替代填充的点阵结构，并映射到连杆中部实体中进行分析，结果如图10 所示。对比分析图8和图10所示的连杆优化前后的Mises应力云图及应变云图，发现填充后最大应力值并未增大，最大应变虽略有增大，但仍满足实际使用要求。

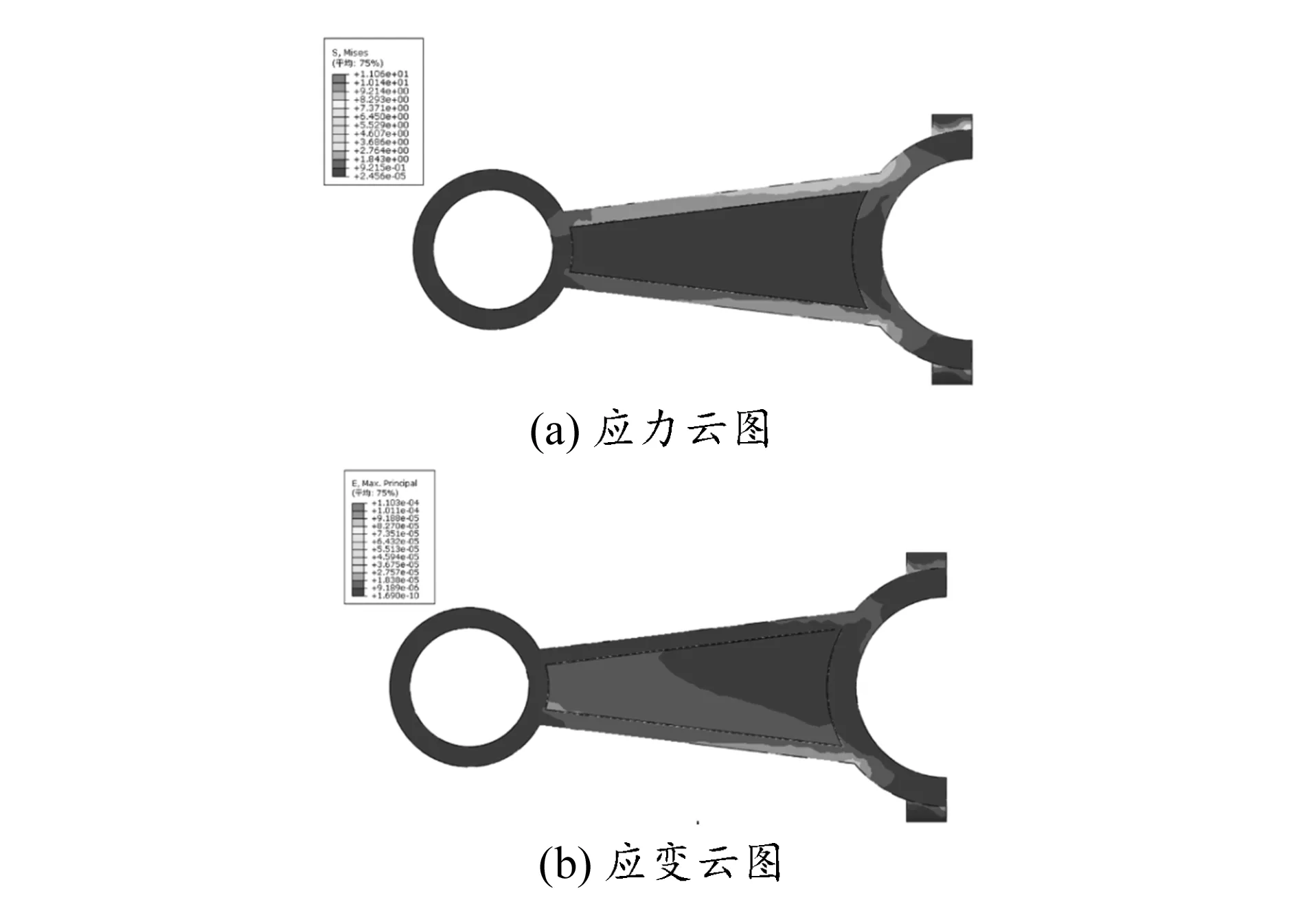
图10 连杆优化后应力应变图

连杆优化前后的位移云图如图11所示。通过对比分析可以发现优化前后云图分布基本一样，最大位移量由填充前的0.011 56 mm增大到0.014 82 mm，体积由80 108 mm3减小到54 750 mm3，减小了1/3，连杆刚度略有降低，但比刚度约是优化前的1.9倍。结果表明，在满足使用要求的前提下，合理应用点阵结构优化连杆的低应力区，可以有效提高连杆结构整体的比刚度。

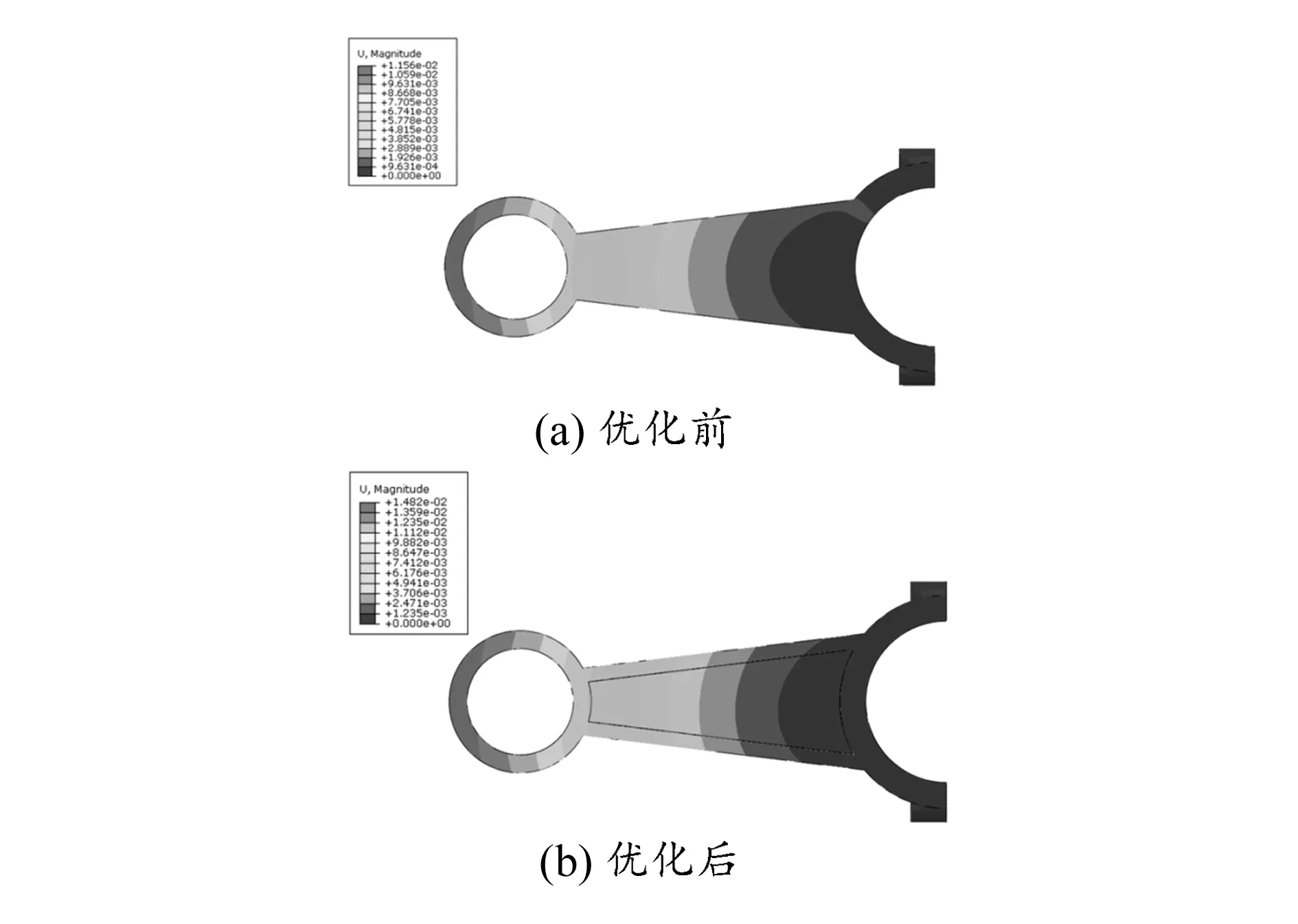
图11 连杆优化前后位移云图

4 结束语

随着增材制造技术的不断发展以及点阵结构各方面优异性能的显现，点阵结构的应用将更加广泛和普遍。虽然点阵结构极具魅力和吸引力，但目前仍然有一些困难使得点阵结构很难用在实际的零件生产中，主要包括点阵结构专用建模软件的开发、点阵结构的力学性能研究、点阵结构其他性能的研究、点阵结构填充分析软件的开发等。航空航天、汽车等领域零件轻量化设计的需求以及医用假体填充结构的设计、新型功能材料的发展需求，使得点阵结构的发展潜力巨大，因此对其进行深入研究意义重大。