东北地区夏季气温的空间分布及时间变化特征

陈欣彤 宋尧东

（民航黑龙江空管分局气象台，黑龙江 哈尔滨150079）

1 概述

众所周知，气温对航空运营的影响是多方面的。飞机发动机推力的设定、机场跑道的设计与建设、飞机载量与油量的配置等都受到气温的影响。为了提高运营效率和效益，航空公司和机场使用者对气温资料非常关注，特别在夏季，气象部门向用户提供逐时、逐日、逐月的气温实测值和预报值。气温对飞行的影响越来越受到国际航空界的重视，国际民航组织和我国民航气象服务标准中，对航空气象服务者提供气温的过程和精度都有明确的条款约束。

中国东北包括黑龙江、吉林、辽宁及内蒙古东北部地区，地处欧亚大陆东岸中高纬度,气候比较寒冷,温度变率较大,气温异常经常发生。因此从区域尺度上对东北地区气温变化进行研究,探讨其时空分布、变化特征及规律,对提高航空运营效率和效益具有重要的现实意义。本文利用经验正交函数分解的方法对东北地区2011-2015 年的夏季气温距平资料进行处理，得到相关空间场和时间序列，分析其时空分布特征，找出其中的规律。

2 资料与方法

本文选取了中国东北地区（38-52°N，120-132°E）23 个气象观测站（呼玛、黑河、齐齐哈尔、海伦、伊春、富锦、绥化、佳木斯、哈尔滨、鸡西、通榆、牡丹江、四平、长春、敦化、延吉、朝阳、沈阳、通化、营口、丹东、瓦房店、大连），时间尺度为五年(2011.1.1-2015.12.31）的夏季（每年的6、7、8 月）气温逐日平均值资料。利用EOF 分解的方法，得到了23 个模态的方差贡献以及空间向量与时间系数数据，并利用其作图得到了东北地区2011-2015 年夏季气温前五个模态的方差贡献曲线及其前两个模态的空间向量场与时间系数序列。

3 经验正交函数分解

E0F 分析方法是一种分析矩阵数据中的结构特征，提取主要数据特征量的一种方法，它能够把随时间变化的变量场分解为不随时间变化的空间函数部分以及只依赖时间变化的时间函数部分。Lorenz在1950 年代首次将其引入气象和气候研究，现在该方法已在海洋和其他学科中得到了广泛的应用。EOF 的基本原理如下：

假设气象要素在m 个站点的n 次观测资料用矩阵Fij表示(i=1，2，…，m；j=1，2，…，n)，利用EOF 方法将Fij分解如式(1)。

式(1)中，Tjk为分解后的时间函数，Xki为分解后的空间函数。当取k=m个特征向量场时，该气象要素场可得到完全的描述。其优点在于典型场由变量场序列本身的特征来确定，而不是事先人为规定，因而能较好地反映出场的基本结构。这种方法展开收敛速度快，很容易将大量资料信息浓缩集中。它能对有限区域内不规则分布的站点进行分解，且分解的空间结构具有明确的物理意义。本文对中国东北地区（38-52°N，120-132°E）23 个气象观测站五年（2011.1.1-2015.12.31）的夏季气温日均值资料进行处理，得到其每个模态的空间向量场、时间系数序列和方差贡献。

4 夏季EOF 分解

对东北地区2011-2015 年夏季（每年的6 月、7 月、8 月）共十五个月的气温距平资料进行EOF 分解，第一模态的方差贡献最大，高达68.7%，第二模态的方差贡献迅速降低至14.9%，前两个模态的累积方差贡献超过80%，其余各个模态的方差贡献均在5%以下。这表明，第一模态的空间向量场很好地解释了东北地区2011-2015年夏季气温距平空间分布特征，而第二模态的空间向量场则对第一模态空间向量场做了很好的补充。

4.1 空间分布特征

图1 是东北地区2011-2015 年夏季气温距平场的第一模态空间向量场。由图1 可以看出，东北地区2011-2015 年夏季气温距平特征向量值全区一致为正，说明东北地区2011-2015 年夏季的气温变化全区总体一致，具体是指东北地区2011-2015 年夏季的气温全区普遍偏高或者普遍偏低。总的来看，东北地区2011-2015 年夏季气温距平场的第一模态空间向量场分布型基本为带状分布，越往中心地区距平特征向量值越大，最大值出现在黑龙江省与吉林省交界处附近，越往南北两侧地区距平特征向量值越小，最小值出现在辽宁省最南部地区。这说明东北地区2011-2015 年在夏季的气温变化全区总体一致的情况下，黑龙江省与吉林省交界处附近地区是夏季的气温变率最大的地区，辽宁省最南部地区是夏季气温变率最小的地区。

图1 东北地区2011-2015 年夏季气温距平场的第一模态空间向量场

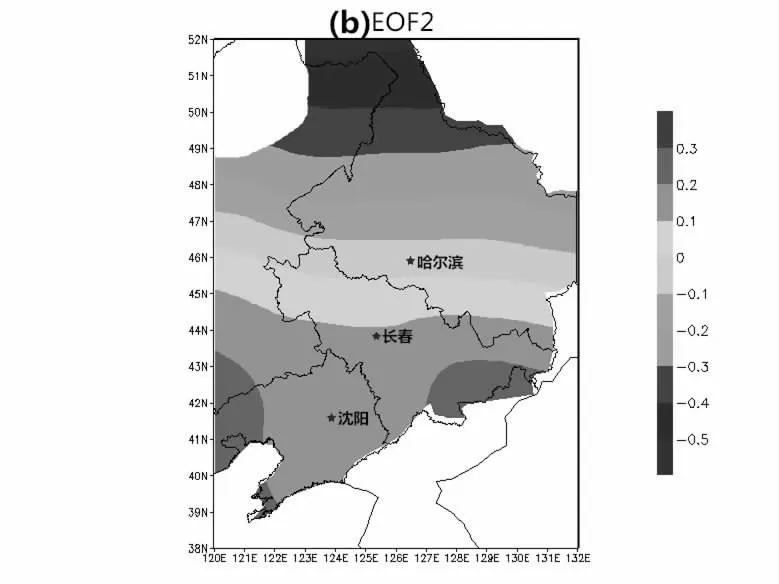
图2 东北地区2011-2015 年夏季气温距平场的第二模态空间向量场

4.2 时间变化特征

图3 是东北地区2011-2015 年夏季气温距平场的第一模态时间系数序列。由图3 可以看出，东北地区2011-2015 年夏季气温距平场的第一模态时间系数随时间呈现出一定的波动变化，波动振幅较大，波动周期大致为一个月。具体而言，东北地区2011-2015年夏季气温距平场的第一模态时间系数有正有负，正值越大气温变化越接近于其距平场第一模态空间向量场的分布，即东北地区2011-2015 年夏季的气温全区普遍偏高，负值越大气温变化越接近于其距平场第一模态空间向量场的反向分布，即东北地区2011-2015 年夏季的气温全区普遍偏低。这说明东北地区2011-2015 年夏季的气温变化随时间呈现出一定的波动变化，变化周期大致为一个月。

图3 东北地区2011-2015 年夏季气温距平场的第一模态时间系数序列

图4 是东北地区2011-2015 年夏季气温距平场的第二模态时间系数序列。由图4 可以看出，东北地区2011-2015 年夏季气温距平场的第二模态时间系数随时间呈现出一定的波动变化，波动振幅明显小于距平场第一模态时间系数的波动振幅，波动周期大致为一个月。具体而言，东北地区2011-2015 年夏季气温距平场的第二模态时间系数有正有负，正值越大气温变化越接近于其距平场第二模态空间向量场的分布，即东北地区2011-2015 年夏季的气温变化南正北负，负值越大气温变化越接近其于距平场第二模态空间向量场的反向分布，即东北地区2011-2015 年夏季的气温变化北正南负。这说明东北地区2011-2015 年夏季的气温变化随时间呈现出一定的波动变化，变化周期大致为一个月。

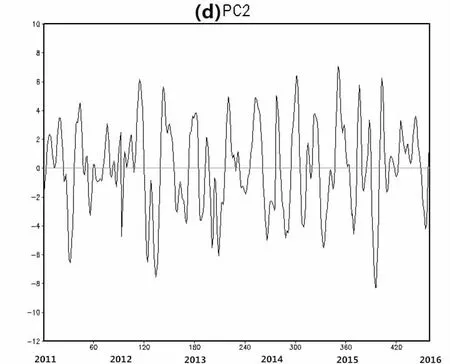
图4 东北地区2011-2015 年夏季气温距平场的第二模态时间系数序列

5 结论

5.1 东北地区2011-2015 年气温夏季距平EOF 分解的前两个模态的累积方差贡献超过80%。

5.2 第一模态空间向量场分布型基本为带状分布，大致呈西南- 东北走向，特征向量值全区一致为正；第二模态空间向量场分布型基本为带状分布，大致呈南北走向，特征向量值南北反向。

5.3 东北地区2011-2015 年夏季气温变化全区总体一致，黑龙江省与吉林省交界处附近地区是夏季气温变率最大的地区，辽宁省最南部地区是夏季气温变率最小的地区，夏季气温变化以黑龙江省与吉林省的交界线为界，表现为南北跷跷板式的第二类空间分布特征。