挠性航天器动力学模型的非约束模态分析1)

宋新宇 戈新生

(北京信息科技大学机电工程学院，北京 100192)

引言

在挠性航天器动力学[1]的研究中，刚体模态表示挠性航天器系统整体的平移和转动；弹性模态表示挠性附件的结构振动.弹性模态为微小振动扰动，叠加在系统整体运动之上.在挠性航天器系统的运动中，由于挠性附件结构的柔性变形所引起的惯性作用将可能导致挠性航天器运动失稳.因此，探讨和研究挠性航天器系统的刚柔耦合作用问题是挠性航天器动力学研究的重点[2].在建立挠性航天器动力学模型时，可以用有限段法[3-4]、有限元法[5-6]、线性弹性理论及假设模态法[7]等方法，对太阳帆板等挠性结构的变形进行描述；挠性多体系统的模型可以用混合坐标法、运动--弹性动力学法和绝对节点坐标法[8]来描述；系统动力学方程可以用牛顿--欧拉法、拉格朗日法、凯恩方法、虚功原理等方法来建立.周志成等针对挠性组合航天器，采用假设模态法和有限元法描述柔性臂杆和太阳翼,通过动量守恒和拉格朗日方法推导了其动力学方程[9].缪炳琪等[10]采用模态综合法建立了挠性航天器的动力学方程.刘伦[11]采用哈密顿原理建立了典型挠性航天器的动力学方程，并提出了一种直接获取挠性航天器刚柔耦合模态的解析方法.袁秋凡等[12]针对小中心刚体--单侧大挠性结构的航天器提出了一种全局模态，并基于哈密顿原理推导了其动力学方程.朱孟萍等[13-14]利用凯恩方法和假设模态法建立了不同类型的挠性航天器的动力学模型.方柳等[15]通过哈密顿变分原理和假设模态法建立了考虑动力刚化效应的挠性航天器的姿态运动和结构振动的偏微分方程.吕旺等[16]利用牛顿--欧拉向量法和模态分析方法建立了挠性卫星的动力学方程.王首喆等[17]采用虚功率原理建立了刚柔液耦合的航天器姿态轨道动力学方程.孟德山[18]针对挠性空间机器人系统，利用递推组级法和模态综合法建立了其动力学方程.魏进等[19]提出复合柔性结构全局模态的解析提取方法，通过全局模态离散得到系统非线性动力学模型，得到系统的固有频率和解析函数表征的全局模态.孙家亮等[20]对近年来多柔体系统动力学建模、动力学优化及结构优化的研究成果和进展进行了综述和总结，并提出了在多柔体系统动力学研究中值得关注的诸多问题.曹登庆等[21]从数个方面对大型挠性航天器动力学与振动控制问题，及在研究中迫切需要解决的诸多基础科学问题作了较为全面的介绍.

利用约束模态和非约束模态，并结合混合坐标法来建立挠性航天器动力学方程是两种主要方法.约束模态定义为中心刚体固定或固连在惯性坐标系上，挠性附件无阻尼自由振动，体现了挠性附件在固定端约束状态下的固有特性.利用约束模态法建立的挠性系统动力学模型，接近挠性航天器在地面进行试验测试的状态.非约束模态定义为中心刚体不固定，整个系统(刚体、挠性附件)的无阻尼自由振动，体现了整星系统的固有特性.利用非约束模态法建立的挠性系统动力学模型，更接近卫星在轨实际飞行状况[22-24].通常情况下，阶数越高的动力学模型所反映的系统动力学特性越精确.但是，模型阶数较高又不利于航天器系统控制设计和应用，因此存在动力学模型降阶问题[25].惯性完备性准则[26-27]常在工程应用中被用于对系统低频模态不太密集的动力学模型进行模态截断和模型降阶[28].所谓惯性完备性，是指对挠性结构质量或惯量的逼近程度.惯性完备性准则实质上就是忽略对挠性耦合系数(即平动挠性耦合系数和转动挠性耦合系数)影响较小的模态，其是一个关于挠性耦合系数与挠性附件质量和惯量等特征相关的恒等式，在工程应用中有着重要的价值.Hughes 等[26,29]深入研究了模态恒等式，给出了惯性完备性准则.徐小胜等[30]曾对约束模态惯性完备性准则给出了详细证明.

在挠性航天器动力学的研究中，一般使用约束模态法对航天器系统进行动力学建模及分析，并利用约束模态下惯性完备性准则对所建立的动力学模型进行模态截断和模型降阶.但是，随着现代空间技术的不断发展，航天器所承担的任务越来越复杂，为保证任务的顺利完成，航天器的规模也越来越大，结构也越来越复杂，中心刚体上通常带有多个大型挠性附件，致使中心刚体在航天器系统中质量或惯量所占的比重越来越小，又因为要保证航天器满足轻质要求，这样势必会使挠性航天器的挠性问题更突出[31].在挠性附件相对于系统质心的转动惯量与中心刚体相对于系统质心的转动惯量比值较大的情况下，采用传统约束模态方法建立系统动力学模型并对其动力学问题进行分析，将会产生偏差[32].

在挠性航天器规模不断变大，结构日益复杂的情况下，本文使用非约束模态法对航天器系统动力学问题进行分析.对于中心刚体附带多个挠性附件的挠性航天器结构，首先利用约束模态和非约束模态方法建立了相应的动力学模型，随后探究两种动力学模型之间的关系，推导了非约束模态惯性完备性准则恒等式.最后，通过数值仿真计算了挠性航天器模型的非约束模态固有频率和振型，并尝试用非约束模态惯性完备性准则的质量关系式对挠性航天器模型进行了验算.

1 挠性航天器系统动力学建模

图1 所示为一个中心刚体B 带有N个附件的挠性航天器系统结构示意图，暂不考虑挠性附件相对中心刚体转动的情况.建立惯性坐标系和本体坐标系分别为Oxyz和Obxbybzb，本体坐标系原点Ob为挠性附件未变形时系统的质心.Ro(t)为航天器质心相对惯性坐标系原点O的矢径；RB(rB,t)和REn(rEn,t)分别为中心刚体上任一质点dmB与挠性附件En上任一质点dmEn到O的矢径；rB和rEn分别为中心刚体上任一质点dmB与第n个挠性附件En上任一质点dmEn到航天器质心Ob的矢径；挠性附件En上任一质点dmEn在变形后的位移为un(rEn,t)；航天器系统的绝对角速度为ω.假定挠性体为小变形，变形后产生的位移为一阶小量，航天器的线位移、线速度也进行线性化处理.航天器的姿态用3-2-1 欧拉角描述，当欧拉角Θ(t)在小角度时可近似为=ω.

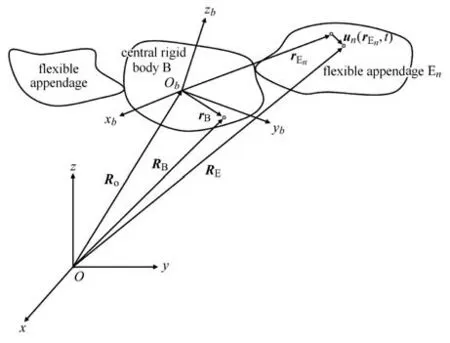
图1 挠性航天器动力学模型Fig.1 Dynamic model of flexible spacecraft

图1 航天器中心刚体上任一质点dmB与挠性附件上任一质点dmEn到O的矢径可分别写为

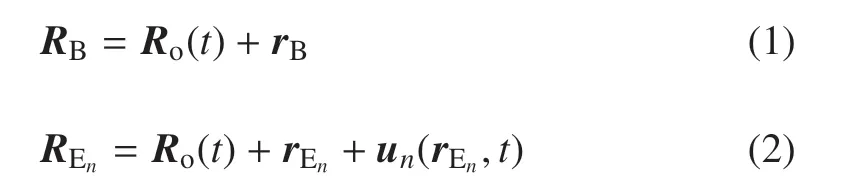
对式(1)和式(2)相对时间求导，可得

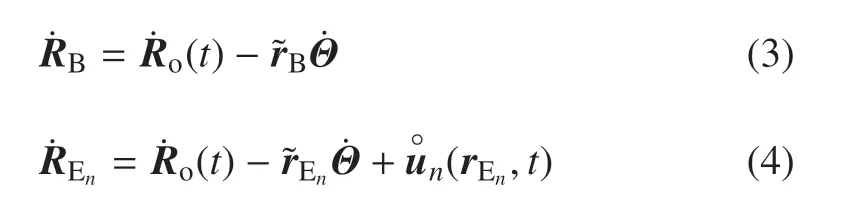
1.1 约束模态

为描述挠性附件的变形，引入模态坐标

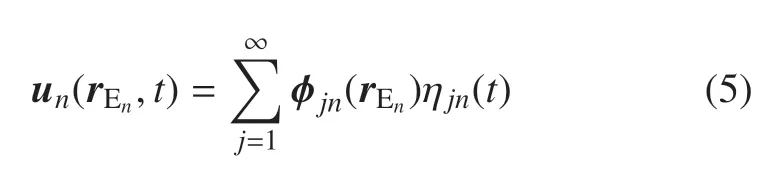
式中，φjn(rEn)为第n个挠性附件En的第j阶模态振型，ηjn(t)为相应的模态坐标，其满足模态正交性条件

式中，ρ(rEn)为挠性附件质量密度，drEn为挠性附件质量微元体积，k为刚度算子，δij为符号函数，Ωjn为第n个挠性附件En的第j阶约束模态固有频率.

根据动量定理、角动量定理推导系统平动与转动方程；根据第二类拉格朗日方程推导挠性附件振动方程.忽略与相关的二阶小量，并注意到系统相对其质心的静矩c=0，可得约束模态航天器系统动力学方程为

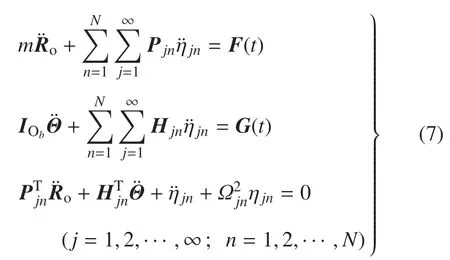
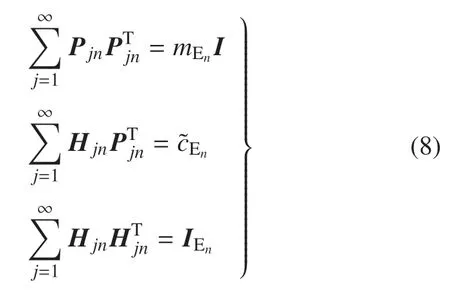
式中，mEn为挠性附件En的质量，I为单位阵，cEn和IEn分别为挠性附件En相对于Ob点的静距和转动惯量.令

则挠性航天器系统动力学方程(7)可写为

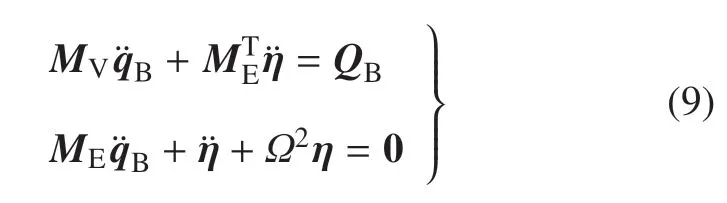
1.2 非约束模态

为了描述非约束模态下系统振动情况，设挠性航天器系统中任一质点的振动位移为w(r)，则

式中，ro(t)和θ(t)为系统振动的刚性平移和转动；r为系统中任一质点到航天器质心Ob的矢径.引入模态坐标，可将系统中任一质点的振动位移为w(r,t)写为

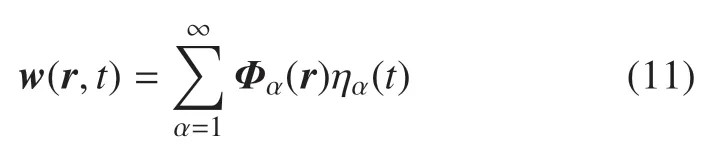
式中，Φα(r)为系统任一质点的非约束模态振型，ηα(t)为相应的非约束模态坐标

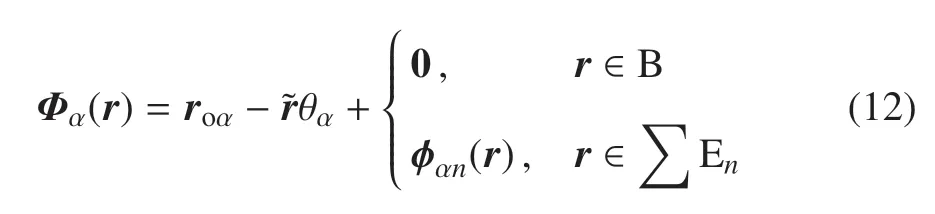
式中，roα和θα为刚体的平动和转动模态，φαn(r)为第n个挠性附件En的第α 阶非约束模态振型.其满足非约束模态正交性条件[23]

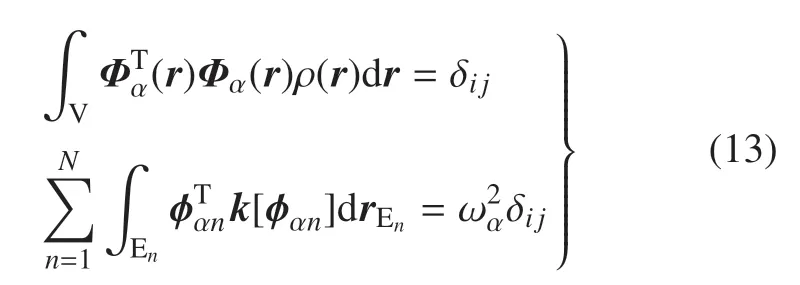
式中，ωα为挠性航天器系统的非约束模态固有频率，积分号中的下角标V 表示积分区域为整个航天器系统.

在非约束模态下，挠性航天器系统的平移和转动可分别表示为

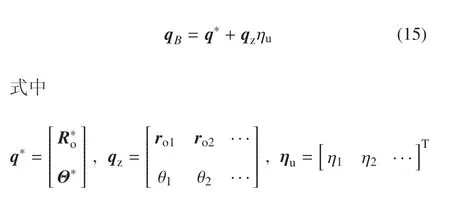
根据动量定理、角动量定理以及第二类拉格朗日方程，可导出挠性航天器系统基于非约束模态下的动力学方程为

因坐标选取在航天器系统质心，平动与转动耦合系数分别满足[23]

则式(16)可写为

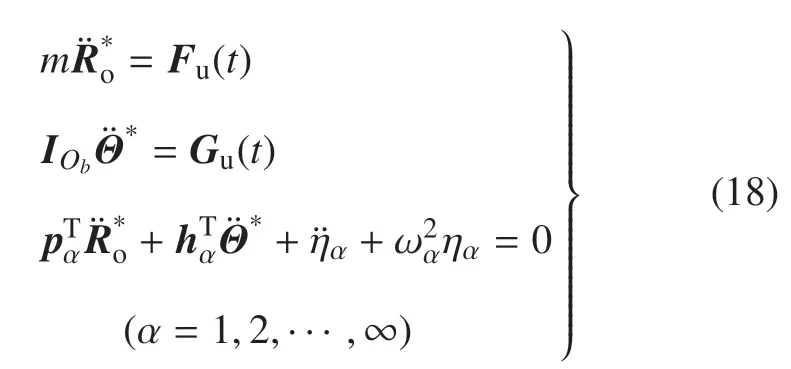
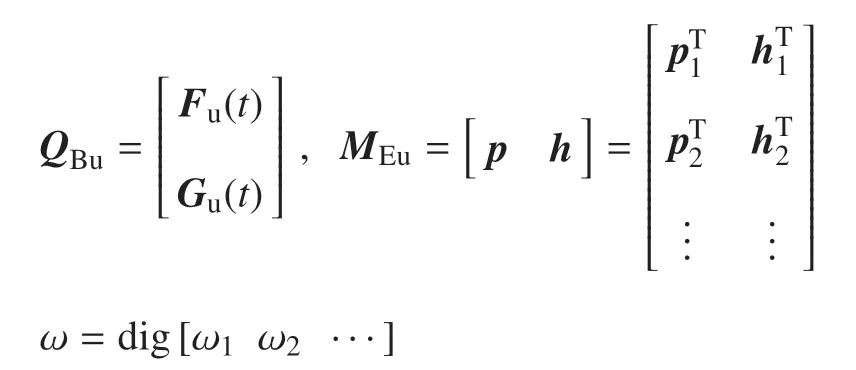
则式(18)可写为

根据式(15)和式(17)，并利用式(19)中的第1 个式子，可将式(19)改写为

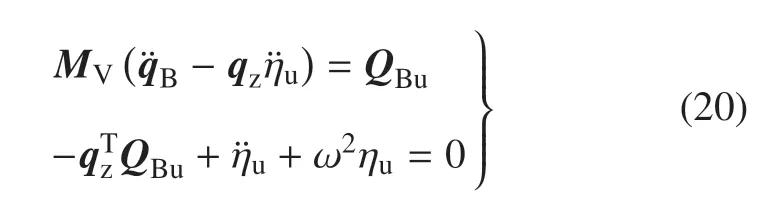
2 非约束模态惯性完备性准则

对约束模态下航天器动力学方程(9)进行拉普拉斯变换，可得

对非约束模态下航天器动力学方程(20)进行拉普拉斯变换，得到

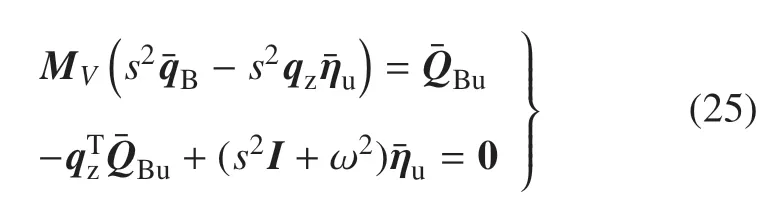
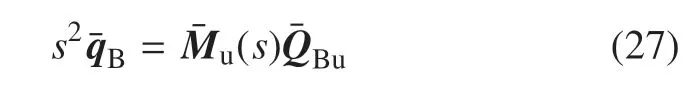
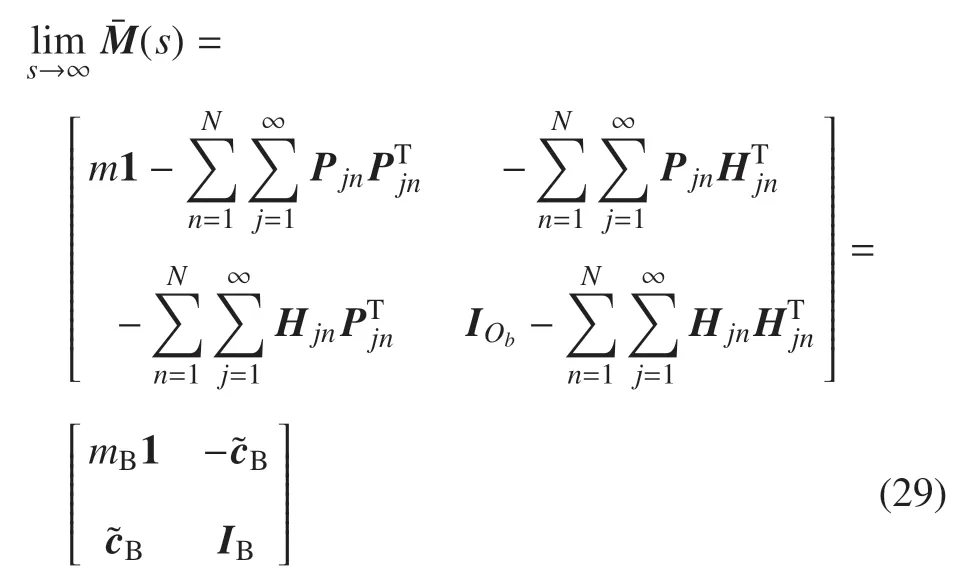
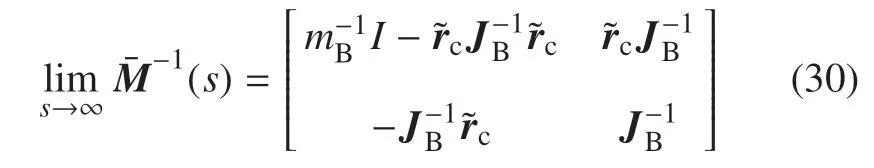
对式(28)求极限，并利用式(17)可得

因系统惯性只与系统本身有关，则式(30)与式(31)应相等，即有

对式(32)两边移项化简后可得

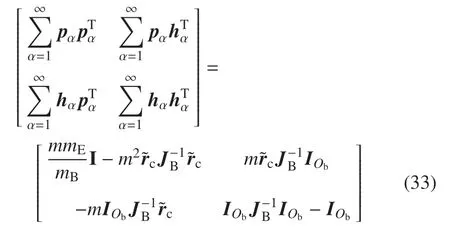
由式(33)矩阵对应元素相等得到非约束模态下惯性完备性准则

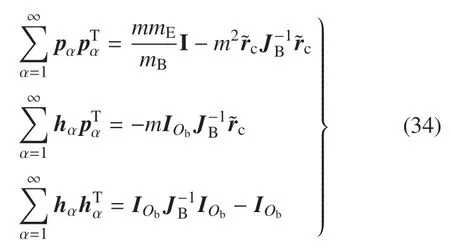
若航天器中心刚体质心与系统质心重合，则恒等式(34)可简化为

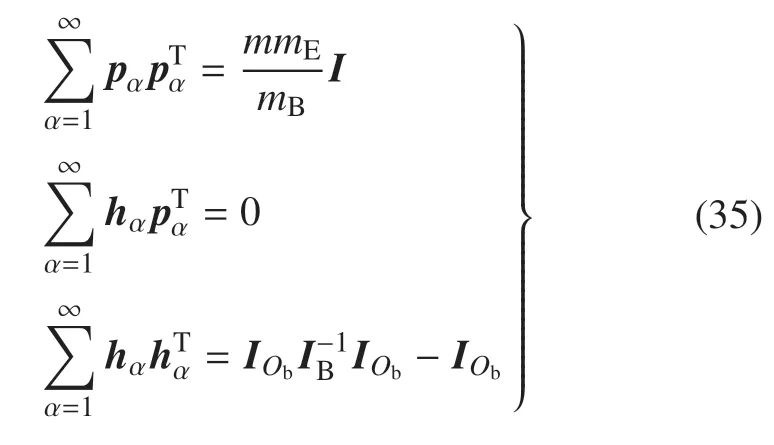
3 数值仿真分析

考虑两种挠性航天器模型，即中心刚体带双侧太阳帆板和带单侧太阳帆板组成的挠性航天器模型.中心刚体为立方体，其材料参数为[33]：杨氏模量E=2.0×1011N/m2，泊松比g=0.3，密度为7800 kg/m3，厚度为0.005 m；太阳帆板的材料参数为[33]：杨氏模量E=2.62×1011N/m2，泊松比v=0.3，密度为920 kg/m3，厚度为0.0015 m，每侧太阳帆板质量为5.209 5 kg.模型整体结构及太阳帆板尺寸图2 所示，其中太阳帆板短边长度为0.1 m.

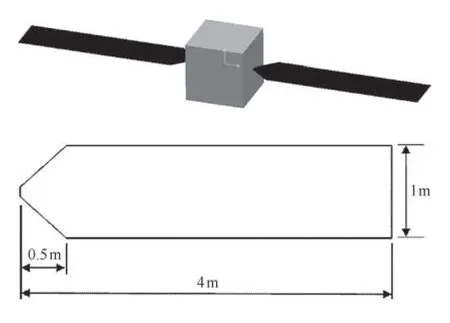
图2 挠性航天器模型及太阳帆板结构尺寸Fig.2 Flexible spacecraft model and structure size of solar array

3.1 算例1

算例1 模型的中心刚体边长尺寸为1.5 m，其质量为523 kg，中心刚体相对系统质心的转动惯量为，挠性附件相对系统质心的转动惯量为IE=kg· m2.不考虑太阳帆板相对中心刚体的转动，利用Ansys 软件对图2 所示的模型进行非约束模态仿真分析，可计算出前6 阶非约束模态固有频率和振型，如图3 所示.

图3 前6 阶非约束模态固有频率和振型Fig.3 Natural frequency and mode shapes of unconstrained mode of the 1st to 6th

图3 前6 阶非约束模态固有频率和振型(续)Fig.3 Natural frequency and mode shapes of unconstrained mode of the 1st to 6th(continued)

在中心刚体相对系统质心的转动惯量大于挠性附件相对系统质心的转动惯量的情况下，计算两种模态的惯性完备性准则关于质量特性恒等式.分别求解太阳帆板前10 阶约束模态平动挠性耦合系数Pjn和前10 阶非约束模态平动挠性耦合系数pα，如表1 和表2 所示.

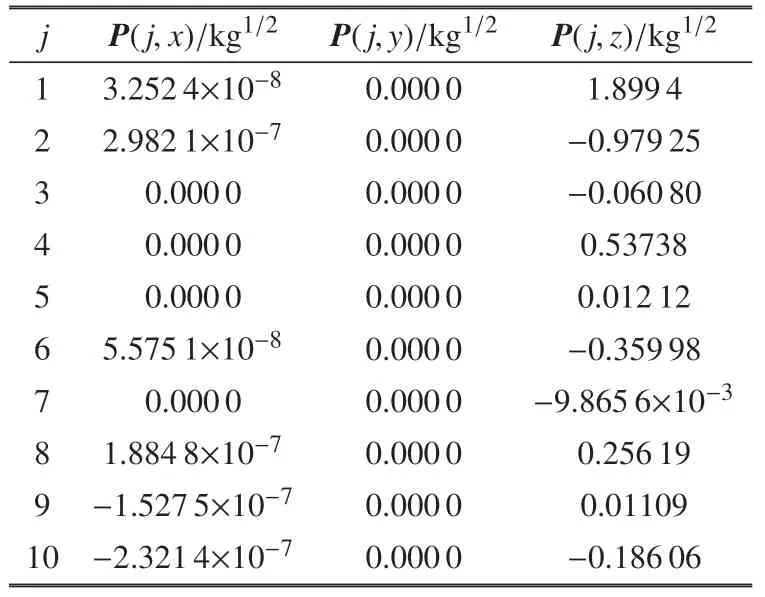
表1 前10 阶约束模态平动挠性耦合系数PjnTable 1 Translational flexible coupling coefficient Pjn of constrained mode of the 1st to 10th

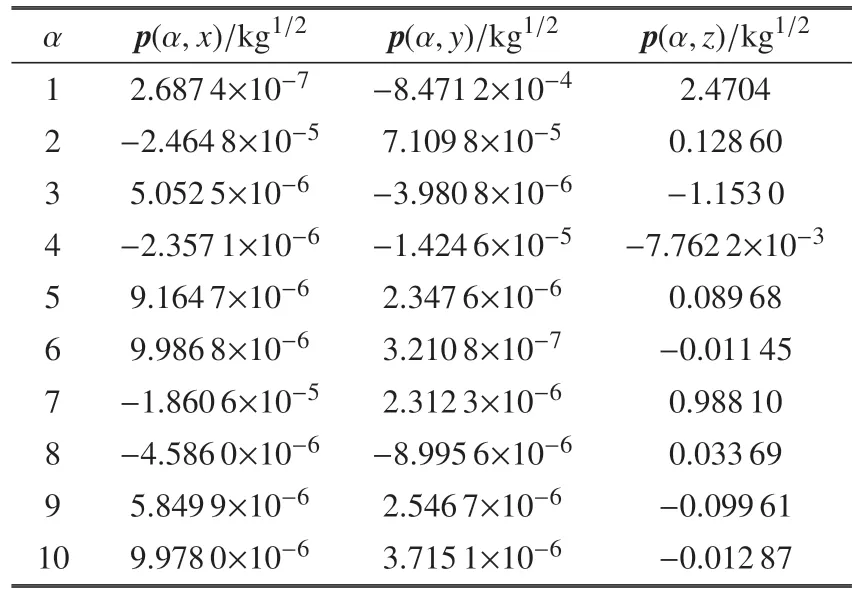
表2 前10 阶非约束模态平动挠性耦合系数pαTable 2 Translational flexible coupling coefficient pα of unconstrained mode of the 1st to 10th

根据式(8)和式(35)以及表1 和表2 的计算数据，分别对两种模态情况下惯性完备性准则中质量特性恒等式的理论值与前10 阶数值求解，得到

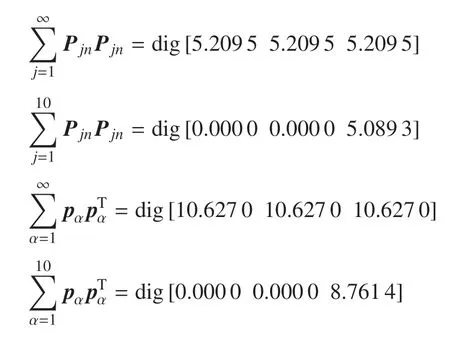
从计算结果可以看出，矩阵中表征太阳帆板在x和y方向上平动的影响系数与理论值不符，其原因在于前10 阶模态对于太阳帆板在x和y方向上的平移影响甚微，可近似视为无影响.

在挠性附件相对系统质心的转动惯量小于中心刚体相对系统质心的转动惯量时，由上述计算结果可以看出，计算结果与模型仿真实验情况相一致，两种模态下前10 阶模态均在z方向上近似满足关于质量特性的惯性完备性准则.

3.2 算例2

在算例1 的基础上，改变中心刚体边长尺寸，其他参数均不变.将中心刚体边长尺寸改为0.5 m，其质量为57.338 kg，中心刚体相对系统质心的转动惯量为IB=dig[3.903 2 3.903 2 3.903 2]kg·m2，挠性附件相对系统质心的转动惯量为IE=dig[70.494 0.837 2 71.331]kg·m2.不考虑太阳帆板相对中心刚体的转动，利用Ansys 软件对模型进行非约束模态仿真计算，可以得到前6 阶非约束模态固有频率和振型，如图4 所示.

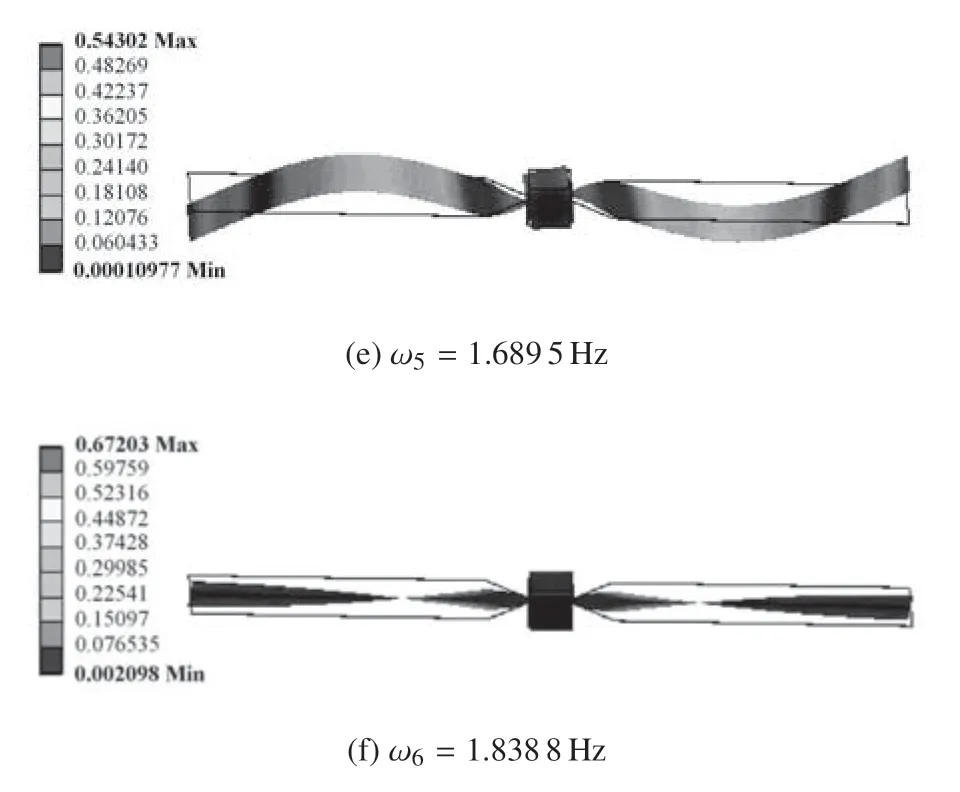
图4 前6 阶非约束模态固有频率和振型Fig.4 Natural frequency and mode shapes of unconstrained mode of the 1st to 6th

当挠性附件相对于质心的转动惯量大于中心刚体相对于质心的转动惯量时，因约束模态方法求解的频率和振型将产生误差，仅考虑非约束模态惯性完备性准则的检测验算.前10 阶系统非约束模态平动挠性耦合系数pα如表3 所示.

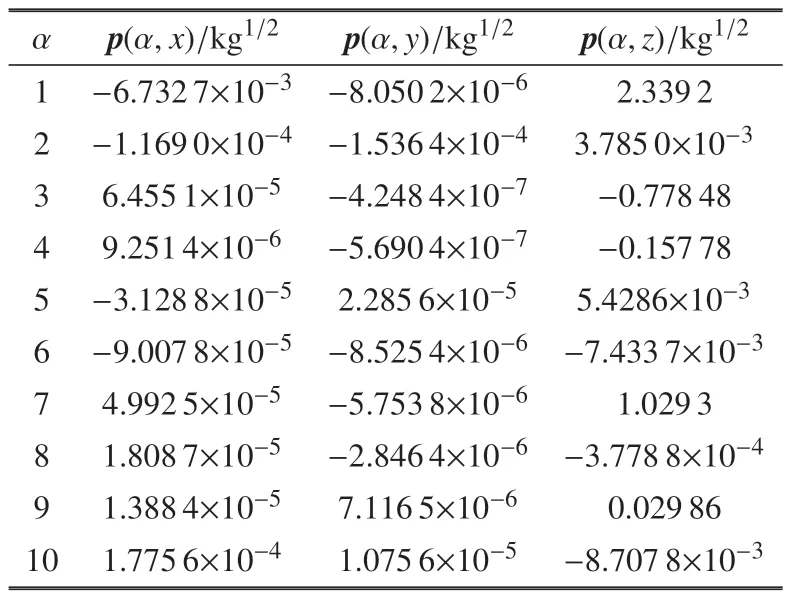
表3 前10 阶非约束模态平动挠性耦合系数pαTable 3 Translational flexible coupling coefficient pα of unconstrained mode of the 1st to 10th

根据式(35)和表3 的计算数据，分别可以求出非约束模态惯性完备性准则中质量恒等式的理论值与前10 阶检测数值，即

上述计算结果中表征太阳帆板在x和y方向上平动影响系数与理论值不符，其原因在于前10 阶模态对于太阳帆板在x和y方向上的影响甚微，可近似视为无影响.在z方向上平动影响系数逐渐向理论值靠近，但误差偏大.若考虑系统模态阶数分别扩大到前20 阶、前30 阶、前40 阶，分别计算可得

对比上述计算结果可以看出，当模态阶数取前30 阶时，表征太阳帆板在x方向上平动的影响系数变为6.0033，这是由于在第29 阶模态时，太阳帆板出现了在x方向上的对称平动.随着所取的模态阶数的增加，实验计算结果逐渐接近理论值，可以近似满足关于质量特性的非约束模态惯性完备性准则.

3.3 算例3

在算例2 的基础上，只保留y轴正方向一侧的帆板，中心刚体质心相对系统质心的坐标为rc=[0 −0.1965 0]Tm，中心刚体相对其质心的转动惯量为JB=dig[3.9032 3.9032 3.9032] kg·m2，其它参数保持不变.此时挠性附件相对系统质心的转动惯量大于中心刚体相对系统质心的转动惯量.不考虑太阳能帆板相对中心刚体的转动，利用Ansys 软件对该单侧帆板模型进行非约束模态仿真分析，计算出前6 阶非约束模态固有频率和振型，如图5 所示.

图5 前6 阶非约束模态固有频率和振型Fig.5 Natural frequency and mode shapes of unconstrained mode of the 1st to 6th

求得前10 阶系统非约束模态平动挠性耦合系数pα，如表4 所示.

根据式(34)和表4 的计算数据，分别计算非约束模态惯性完备性准则中质量恒等式的理论值与前10 阶数值，得到

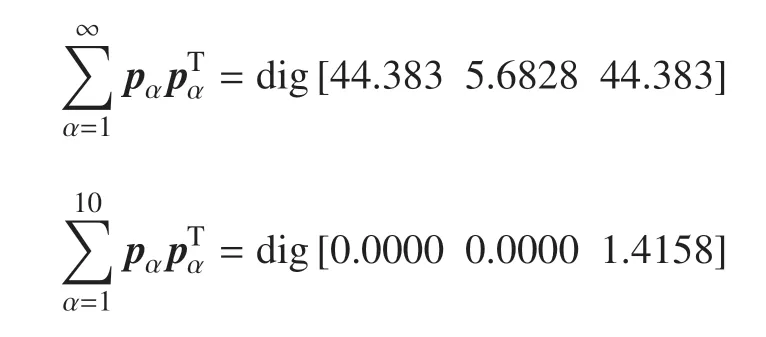
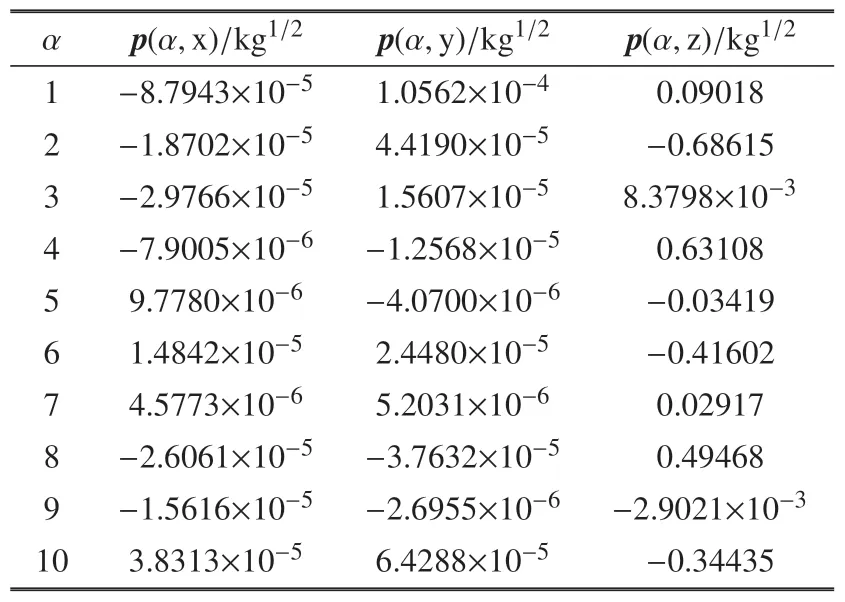
表4 前10 阶非约束模态平动挠性耦合系数pαTable 4 Translational flexible coupling coefficient pα of unconstrained mode of the 1st to 10th

对比计算结果可以看出，前10 阶计算值与理论值不符，其原因在于，当挠性附件相对系统质心的转动惯量大于中心刚体相对系统质心的转动惯量时，单侧帆板模型的各阶非约束模态对帆板在3 个方向上平动影响甚微，帆板的低阶模态集中表现为弯曲和扭转，因此采用关于质量特性的非约束模态惯性完备性准则对此类模型进行降阶无实际意义，应考虑利用关于惯量特性恒等式的惯性完备性准则对其进行检测.

4 结论

本文利用了混合坐标法建立了挠性航天器动力学模型，采用约束模态和非约束模态对航天器的振动进行展开，从而建立了挠性航天器动力学方程，探讨了两种模态情况的系统动力学方程关系.虽然约束模态和非约束模态的系统动力学方程形式有差异，但是其与系统本身相关的特征(即系统惯性)是不变的，推导出了非约束模态惯性完备性准则；随后，利用Ansys 软件对算例模型进行非约束模态数值仿真分析，检测验算了关于质量特性的非约束模态惯性完备性准则.仿真实验结果表明：

(1)当挠性附件相对于系统质心的转动惯量小于中心刚体时，约束模态和非约束模态的计算结果均在z方向上近似满足关于质量关系的惯性完备性准则.

(2)当挠性附件相对于系统质心的转动惯量大于中心刚体时，随着所选取模态阶数的增加，实验计算结果越来越接近理论值，可近似满足关于质量特性的非约束模态惯性完备性准则.

(3)对于挠性附件相对于系统质心的转动惯量大于中心刚体的单侧帆板挠性航天器模型，非约束模态对太阳帆板在3 个方向上的平动影响甚微，计算结果不满足关于质量特性的非约束模态惯性完备性准则，应考虑利用关于惯量特性的非约束模态惯性完备性准则对其进行检测验算.

综上所述，受限于模型各阶模态对帆板在3 个方向上平动的影响，应选用惯量恒等式的惯性完备性准则进行模型检测以及降阶研究，这也是作者下一步开展研究工作的重点问题.