最大容量路的扩张问题研究

刘 耕

（中国地质大学 经济管理学院，湖北 武汉 430074）

1 问题概述

我们生活在一个网络世界中：公路网、铁路网为我们出行和运输物资提供了方便；电力网为我们提供了能源；电信网为我们传递信息。随着人口的增加、技术的发展，对网络的要求也不断提高，网络容量也在不断扩张。2018年末，全国公路总里程达到485万km，是1949年的60倍；根据《电力发展“十三五”规划》，预计2020年全社会用电量6.8-7.2万亿kw·h，年均增长3.6%-4.8%，全国发电装机容量20亿kw，年均增长5.5%。每年要花费巨资对网络进行建设和改造。如何制定最科学的方案，将网络容量扩张到指定值，是我们不得不考虑的问题。

路是网络中比较基本的概念，其有效算法可以在其它网络优化问题中作为子算法调用。在现实中，对网络的扩张往往是从路的改造开始的。在发生紧急情况时，我们往往更关注某些节点之间的路的容量问题。比如，连接起点与终点间的路的容量问题，通常要求这两点间路的容量尽可能大，以便运输尽可能多的物资，这也是本文所研究的主要内容。

方华提出了改造牵引种类、提高牵引质量、增建二线等的铁路扩能改造方案[1]；王蓉将道路网抽象为网络，寻找扩容关键边，并将其与产生的逆向车道备选路段相结合，得到交通疏散逆向车道最优路段选择方案[2]；高明霞等研究了在交通疏散中，通过对最大流增流关键边所对应路段进行逆向管理扩容，能够有效压缩疏散时间[3]；侯志伟等使用最大流和堵塞流的相关理论，得到关内外道路合理扩容的方案[4]；刘耕研究了多阶段情形下的容量扩张问题[5]。

上述作者研究的网络改造问题，主要是通过弧改进的方式进行，而现实中存在多种调整方式。

定义：对于一对节点vs,vt,定义Ls-t为从vs到vt路的集合{l1,l2,…,ln}，定义路lk的容量为路lk上的弧的容量最小值，定义节点对vs-vt之间的路的容量为{l1,l2,…,ln}中容量的最大值，即最大容量路L(vs,vt)的容量，则有：

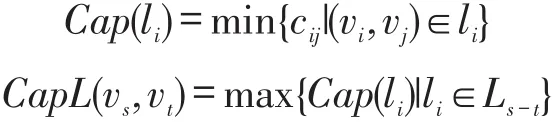
网络容量的扩张有如下几种方式：

（1）弧改进。在这种情形下，通过对弧(vi,vj)上的容量cij进行改造，使得网络容量提高；弧(vi,vj)上增加的容量记为αij，单位改进费用记为 βij；这是一种常见的方式，日常生活中，道路的加宽、管道的加粗都属于这种情形。

（2）点改进。在这种情形下，通过对节点vi进行改造，使得从节点vi上发出的弧(vi,vj)上的容量都提高相同的数值αi，单位改进费用为 βi。日常生活中，天然气管网中增压泵的安装，可看作是点扩张的例子。

（3）弧改进与点改进相结合。即在网络改造中，既有弧改进，也有点改进，二者可同时进行。如在供热管网的改造过程中，既需要管段的扩建，也需要增设加压泵站。

2 问题的一般模型和求解

现在讨论节点对vs-vt的容量扩张问题，即将从vs-vt的最大容量路L(vs,vt)的容量扩张到给定值R0，要求扩张费用D最小。

针对此问题，我们分别按照网络容量扩张的三种方式展开讨论。

（1）弧改进情形下的网络扩张问题。此时的网络容量扩张是通过对弧的改造而实现的，问题表述如下：

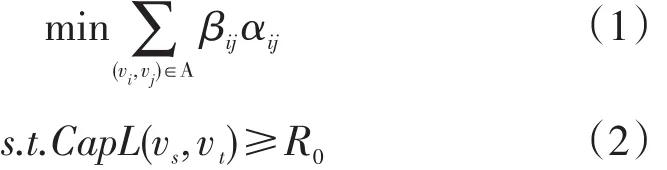
目标函数式（1）表示弧改进成本最小化，式（2）表示扩张后新的最大容量路L(vs,vt)的容量约束。

（2）点改进情形下的网络扩张问题。此时的网络容量扩张是通过对节点的改造而实现的，问题表述如下：

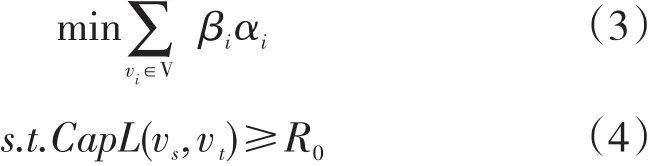
目标函数式（3）表示点改进的成本最小化，式（4）同式（2）。

（3）弧改进和点改进相结合下的网络容量扩张问题。此时的网络容量扩张方式既有弧改进，也有点改进，问题表述如下：

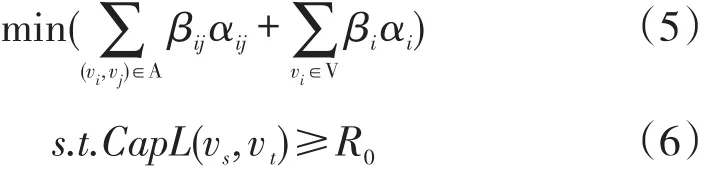
目标函数式（5）表示总的改进成本最小化，式（6）同式（2）。

对于上述问题，我们可以把它们转化为最短路问题。构建辅助网络G（V，A，W），V，A定义如G（V，A，C），W的分量 ωij定义如下：

（1）弧改进情形下

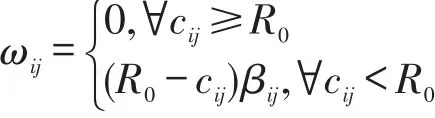
（2）点改进情形下

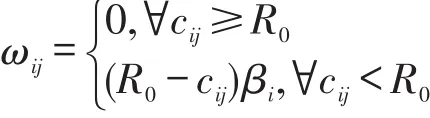
（3）弧改进和点改进相结合

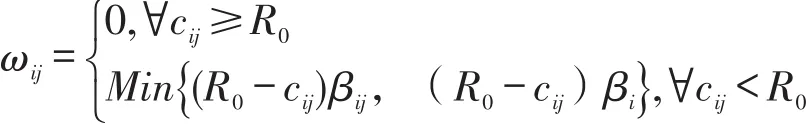
可以看出，单独的弧扩张或点改进是其中的一种特殊情形。

原问题转化为网络G（V，A，W）中的vs-vt最短路问题，可以采用Dijkstra算法求解.

3 算例分析

在如图1给定的有向网络G（V，A，C）中，弧旁的数字表示网络的容量，表1表示弧的单位容量改进成本，表2表示节点的单位容量改进成本。现在要求将路1-6的容量扩张到4，使扩张费用最低。

图1 网络图

表1 弧的单位容量改进成本

表2 节点的单位容量改进成本

如前所示，建立辅助网络G（V，A，W），针对网络扩张的三种情形进行讨论。

在弧改进的情形下：从节点1到节点6的最大容量路为：1-3-4-6。此时的改进方案为：弧（3，4）提高3个单位，其它弧不变；改进费用为9。

在点改进的情形下：此时的最大容量路为：1-2-4-6。此时的改进方案为：节点1改进1个单位，节点2改进1个单位，其它节点不变；改进费用为6。

在弧改进和点改进相结合的情况下：此时的最大容量路为1-2-4-6。改进方案为：弧（1,2）改进1个单位，节点2改进2个单位，其它弧和节点不变。此时的改进费用为4。

可以看出，在弧改进和点改进共同作用的情况下，扩张费用最低。

4 结语

本文研究了有向网络中最大容量路的扩张问题。现实生活中，网络的扩张往往是通过对路的扩张进行的。在发生紧急情况网络被破坏时，前方急需物资，此时比较明智的做法是对原有网络进行改造，从起点到终点找到一条最大容量路，保证其通畅。本文所建立的数学模型具有较大的实用价值。我们将进一步考虑：在网络扩张过程中，限制扩张的弧的数量时，如何提高网络容量。