集装箱远洋多式联运网络配流问题研究

辜 勇，袁源乙，李 雨，陈 句

（武汉理工大学 物流工程学院，湖北 武汉 430063）

1 引言

自“一带一路”战略实施以来，我国社会经济蓬勃发展，交通运输行业也进入了新的发展阶段。多式联运凭借其能加快物流流转效率的优势，在国际货运中的重要性日益增加。虽然“一带一路”战略实施使陆路通道的作用日渐加强，但国际集装箱运输主要还是通过海上通道来完成的。以21世纪海上丝绸之路为主干线的远洋运输系统为例，各路段的承运能力有限，各节点的通过处理能力有限，当大批量货物进行多式联运时，需要根据各种运输方式的特点，从系统层面综合考虑运输网络现状进行统一配流，达到运输网络平衡，实现通道运力与货流量合理配置，具有较高现实意义。由于集装箱运输是发展多式联运的载体，本文以集装箱运输为研究对象。

关于集装箱运输网络的配流问题研究，Bell等[1]以海上集装箱运输为研究对象，引入港口单位时间可以处理的最大集装箱数量为约束建立海运集装箱配流模型。陈丽芬等[2]建立以运输费用最小化为目标的负指数网络配流模型，并采用偏好因数对模型进行改进，将环渤海地区集装箱运输网络配置作为算例，对网络中的货流路径进行分析和预测，以此协调网络运载负荷。王丹，等[3]不仅引入偏好系数，还引入时间成本，建立了包含时间成本的负指数网络配流模型，对包括东北航道在内的多个运输通道进行集装箱货配流。由于负指数网络配流模型没有考虑到运输网络中节点作业处理能力和线路运输能力约束，在实际应用中具有一定局限性。当考虑通道运力限制时，高山山等[4]针对冷藏箱集疏运系统，以综合运输成本最小为目标函数构建了流量分配优化模型，并以驳船冷藏箱载箱量为自变量进行灵敏度分析，探讨运力释放对总成本的影响。当同时考虑节点与通道作业能力时，潘静静等[5]针对海港集疏运网络的货物流量分配问题，将网络运输总成本最小作为目标，建立线性整数规划模型，并以福建为例对模型进行应用和验证。在网络配流模型求解算法方面，近些年学者们运用智能启发式算法来求解交通配流问题，陈能成，等[6]通过对路网通行能力的分析，提出了一种基于改进蚁群算法的交通流量分配方法。Wang等[7]针对公铁联运问题建立带有时间窗的集装箱货流分配模型，并运用混合禁忌搜索算法求解。魏海蕊等[8]根据海港与无水港合作关系特征，建立了腹地-无水港-海港可持续物流系统布局与货流配置的双目标混合整数规划模型，并利用多目标遗传算法求解。

以上文献中很少有将节点作业能力和通道运输能力同时考虑到集装箱多式联运网络中，且大多将海运部分当作一个整体，很少考虑远洋航线海运中转节点选择问题，而中转海港是实现集装箱远洋运输的关键节点。由于集装箱多式联运货流分配问题的复杂性，关于此类模型的求解算法研究还相对很少。因此本文构建了远洋运输系统成本最优的多式联运配流模型，并设计多层编码遗传算法求解，以期从网络配流的角度对集装箱远洋多式联运网络建设提供一定参考。

2 模型构建

2.1 问题描述

集装箱远洋多式联运网络是以箱源供需地和海港为节点，以连接节点的运输线路为弧建立的网络。以远洋出口集装箱为例，假设网络中O为箱源地节点集合，通过i索引；S为始发港节点集合，通过s索引；K为中转港节点集合，通过k索引；P为目的港节点集合，通过 p索引；D为目的地节点集合，通过 j索引。内陆节点与港口节点由L种运输方式连接，通过l索引（l=1为公路运输，l=2为铁路运输）。海运部分港口节点间有直达航线，也有中转航线，如图1所示。

为将现实的复杂问题抽象为数学模型，对远洋出口集装箱运输网络做出如下假设：

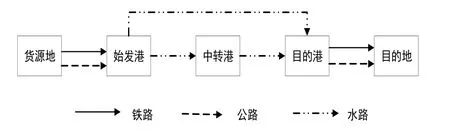
图1 基于多式联运的远洋出口集装箱运输网络

（1）假设货物种类都是20尺标箱。

（2）运输网络为固定网络，所有网络路线和节点都为已知。

（3）转运过程产生的费用全部算入转运成本，除此之外不计货物的延迟成本或储存成本。

（4）海陆装卸过程中为整箱装卸，不会产生货损。

（5）同种运输方式在不同路径的单位运输成本一致。

2.2 模型建立

以集装箱运输总成本最小化为目标，构建多式联运网络配流模型为：

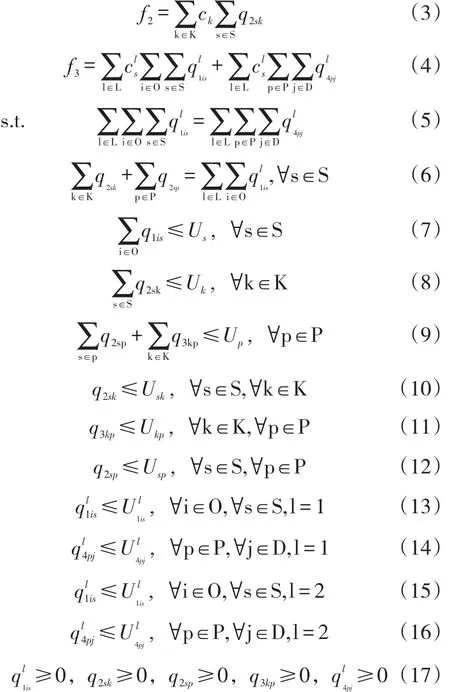
式（1）表示多式联运网络运输总成本；式（2）表示集装箱运输成本；式（3）表示港口与港口之间的转运成本；式（4）表示内陆运输与海上运输之间的转运成本；式（5）表示供需流量守恒；式（6）表示经海运中转的流量也守恒；式（7）表示始发港的通过能力约束；式（8）表示海运中转港的通过能力约束；式（9）表示目的港的通过能力约束；式（10）-（12）表示海港间的运力约束；式（13）-（14）表示公路运力约束；式（15）-（16）表示铁路运力约束；式（17）表示决策变量的非负整数约束。

3 算法设计

遗传算法是模拟生物进化规律的一种启发式算法，具有较好的解决全局优化能力。本文采用遗传算法对模型进行求解。

3.1 染色体编码与解码

本文集装箱多式联运网络结构中共有五个层次：货源地-始发港-中转港-目的港-目的地，设计基于五层编码的遗传算法。第1层编码针对货源地至始发港的路径指派和货量分配，编码长度等于货源地数量与始发港数量之积，基因位为[-1,1]区间随机产生的实数。比如有2个货源地，4个始发港，为便于理解，将货源地看作供应点，始发港看作需求点，其余层编码也作同样处理。一个合法的染色体可表示为[0.90,-0.85,0.86,0.32,-0.64,0.13,0.58,-0.56]，将编码转换为矩阵A如下：

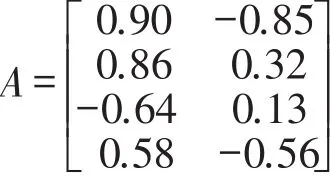
其编码意义为：当矩阵中元素A(i,j)≤0时，需求点i不由供应点 j提供服务；当矩阵中元素A(i,j)＞0时，需求点i由供应点 j提供服务。比如需求点1对应编码是0.90，-0.85，则需求点1仅由供应点1满足其全部需求量，供应点2没有货物运往需求点1；需求点2对应编码是0.86，0.32，则供应点1和供应点2都将有货物运往需求点2。货流分配量按比例进行分配，分配比例根据矩阵A中元素值确定。矩阵第一行对应第1个需求点编码，大于0的元素是A(1,1)，则第1个需求点的需求量Q1全部由供应点1提供。矩阵第二行对应第2个需求点，可知第2个需求点对应备选供应点是1和2，则供应点1分配到需求点2的货物比例p1=0.86/(0.86+0.32)，需求点2的需求量为Q2，供应点1分配到需求点2的货物量=p1*Q2，供应点2分配到需求点2的货物比例p2=0.32/(0.86+0.32)，供应点2分配到需求点2的货物量=p2*Q2。

第2层编码针对始发港至中转港的路径指派和货量分配，编码长度等于始发港数量与中转港数量之积，基因位为[-1,1]区间随机产生的实数，其编码意义类似于第1层编码。

第3层编码针对始发港至目的港的路径指派和货量分配，编码长度等于始发港数量与目的港数量之积，基因位为[-1,1]区间随机产生的实数，其编码意义类似于第1层编码。

第4层编码针对中转港至目的港的路径指派和货量分配，编码长度等于中转港数量与目的地数量之积，基因位为[-1,1]区间随机产生的实数，其编码意义类似于第1层编码。

第5层编码针对目的港至目的地的路径指派和货量分配，编码长度等于目的地数量与目的地数量之积，基因位为[-1,1]区间随机产生的实数，其编码意义类似于第1层编码。

父代染色体经过复制、交叉、变异处理后，得到子代染色体结构，对子代染色体进行解码。解码分为四个阶段，由后层往前层解码，第一阶段解码是将目的地D分配到目的港P，得到指派路径，根据每个目的地的需求量按比例计算得到其从某个目的港运往的货量，且货量值不大于路径运输能力，某个目的港总输出量不能超过该港的节点通过能力，并将该港输出总量作为需要从其它节点供应的需求量；第二阶段解码是将目的港P分配到中转港K或始发港S；第三阶段解码是将中转港K分配到始发港S；第四阶段解码是将始发港S分配到货源地O；第二阶段至第四阶段各路径上的货量分配参照第一阶段处理。

3.2 遗传操作

（1）选择。从初始种群中选出适应环境的个体用于繁殖后代，利用轮盘赌法对种群进行选择操作，个体被选中的概率与其适应度函数值成正比。本文目标函数为minZ，通过解码染色体得到总成本为Z，设定适应度函数为F=1/Z。设群体大小为n，个体i的适应度为Fi，则个体i被选中遗传到下一代群体的概率Pi为：

（2）交叉。交叉算子一般包括单点交叉、多点交叉、均匀交叉。交叉操作又被称为重组操作，选中用于繁殖下代的个体，随机选择具有相同位置的两个个体，按交叉概率实行重组。本文采用两点交叉，两点交叉过程如下：随机选择两个染色体作为父本，产生两个随机自然数r1和r2，将两个父本染色体r1至r2之间的基因片段进行交换，得到两个子代染色体。

（3）变异。采用单点变异，具体过程如下：产生一个随机自然数r1,r1表示第r1位的基因发生变异，采用随机变异的方式将第r1位的基因进行变异。

4 算例求解

从“21世纪海上丝绸之路”沿线国家的双边贸易情况看，中国与印度的双边贸易量相对较大，故选取中国与印度为本案例涉及的OD对国家。福建作为21世纪海上丝绸之路的起点，本文选取福建省内区域为货源地，根据文献[5]，以泉州陆地港、龙岩陆地港、三明陆地港和南平陆地港作为集装箱发货地，分别标记为O1、O2、O3和O4。福州港、厦门港、泉州港作为始发港，分别标记为S1、S2和S3。根据全球主要班轮船公司的航线情况，选取香港港、新加坡港、巴生港和科伦坡港作为中转海港，分别标记为K1、K2、K3和K4。孟买港、尼赫鲁港、金奈、皮帕瓦夫和维沙卡帕特南港作为收货地的海港，分别标记为P1、P2、P3、P4和P5。收货地为孟买、浦那、海得拉巴和艾哈迈达，巴德作为集装箱需求地，分别标记为D1、D2、D3和D4。

集装箱单位运输成本为每箱每公里运输费用乘以运距，公铁水3种运输方式的单位成本设定为5元/（km·TEU），1元/（km·TEU），0.5（km·TEU）。内陆运输与海运之间中转费以及海港与海港间中转单位服务成本为集装箱的装卸费，设定为10元/TEU。中国陆地港到沿海港口的运输方式考虑公路和铁路两种方式，而由于印度陆上集疏运体系以铁路为主要运输工具，此处印度港口到内陆城市间均采用铁路运输。

根据海关统计2018年福建省出口印度的贸易额为237 550万美元，运用集装箱生成计算公式式（19），测算出福建省出口印度的集装箱数量。

式中，Q为出口集装箱生成量，TEU，V为周期内出口外贸总额（单位：万美元），a为外贸出口适箱货金额比率，m为外贸出口适箱货重量系数（单位：t/万美元），b为外贸出口集装箱箱化率，%，W为外贸出口重箱平均载重量（单位：t/TEU）。

根据福建省外贸发展水平及发展潜力，货种结构和集装箱发展情况，设a取80%，m取4.5，b取75%，W取9。经测算得到福建省出口印度的集装箱生成量为71 265TEU，取值71 300TEU。假设O1、O2、O3和O4的集装箱年发货量分别为：21 300 TEU、22 000 TEU、5 000 TEU和23 000 TEU。D1、D2、D3和D4集装箱年需求量分别为24 000 TEU、9 700 TEU、29 000 TEU和8 600 TEU。节点间运输里程见表1、表2，节点通过能力约束见表3，海上运输能力约束见表4。

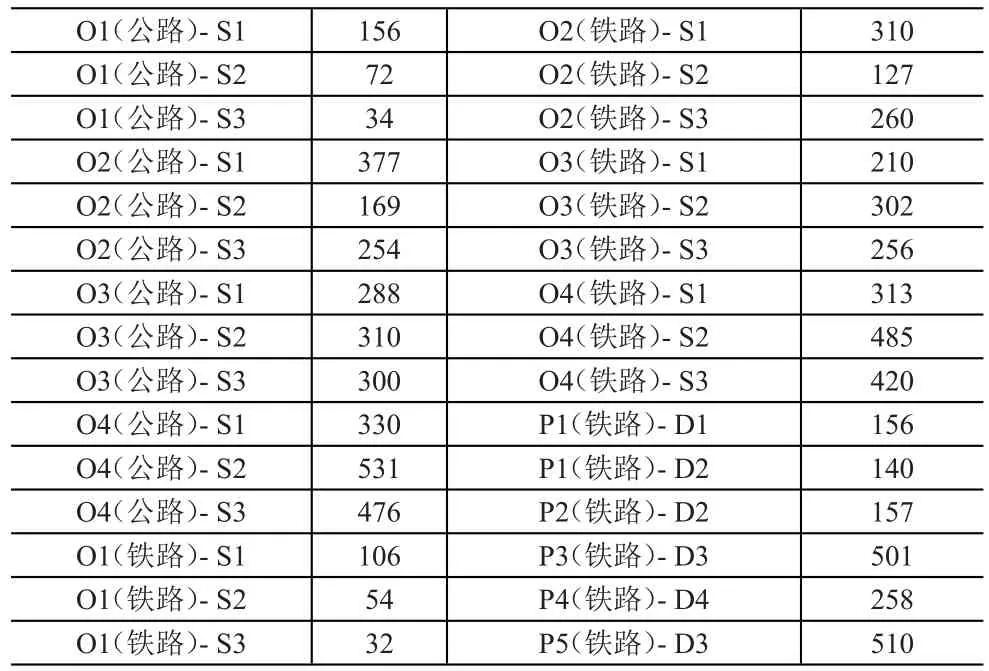
表1 内陆城市与沿海港口运输里程（km）

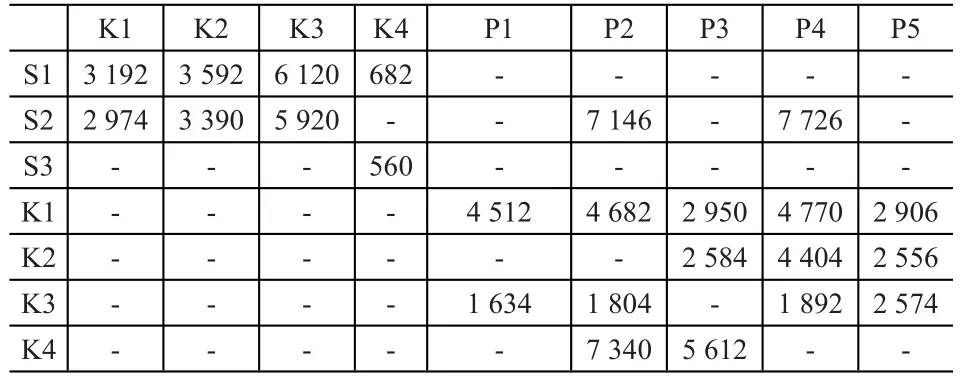
表2 海港之间里程（km）

表3 节点通过能力约束（TEU）

当前陆路运输资源基本能够满足箱源地到起运港的运输要求，所以此处只考虑海运段集装箱运力的限制。

运用MATLAB软件对遗传算法进行程序编写，并对上述算例进行仿真运算，设置参数如下：种群规模Popsize=1 000，交叉概率PC=0.8,变异概率PM=0.2，迭代次数Maxgen=300，经过多次反复运行得到总成本最小的配流方案，见表5-表8。最小总成本值为302 371 100元，最优配流方案出现时的算法收敛曲线图，如图2所示。

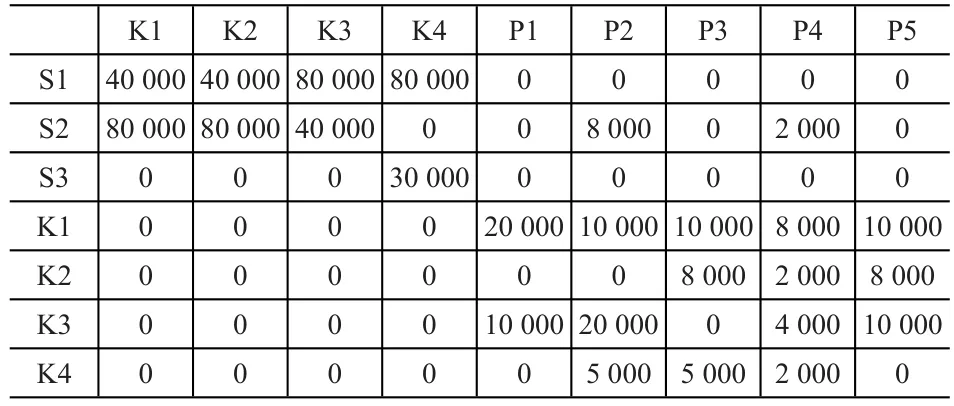
表4 海上运力约束（TEU）

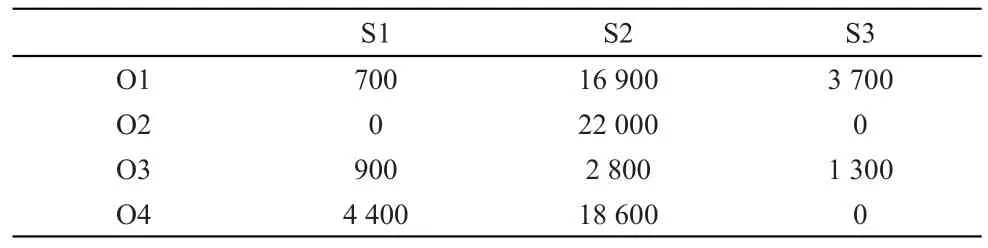
表5 从货源地到始发港集装箱分配量

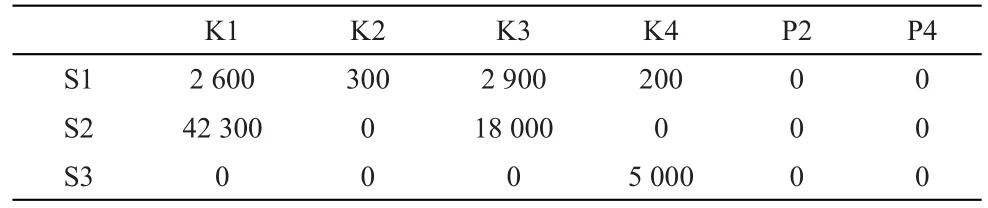
表6 从始发港到中转港和目的港集装箱分配量

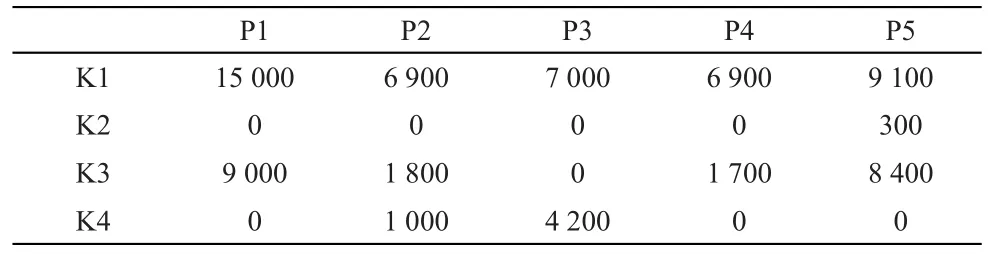
表7 从中转港到目的港集装箱分配量

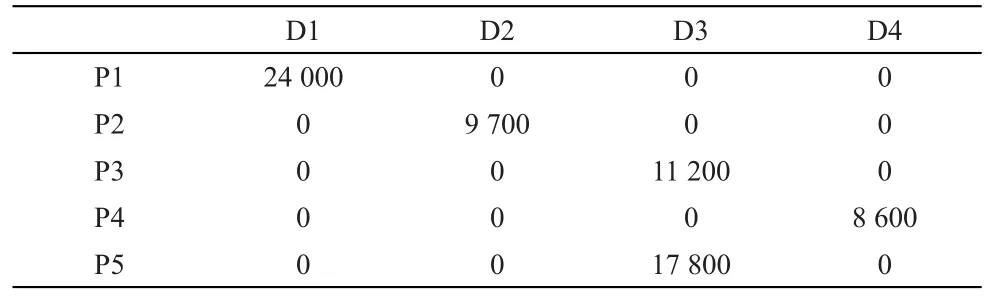
表8 从目的港到目的地集装箱分配量

5 结语

考虑运输方式、运输成本、容量限制等影响因素，构建了远洋集装箱多式联运网络货流分配模型，并设计多层编码的遗传算法求解。通过算例分析验证了模型算法的可行性，有助于实现集装箱远洋运输系统资源合理配置，为集装箱多式联运系统优化提供了有价值的参考。

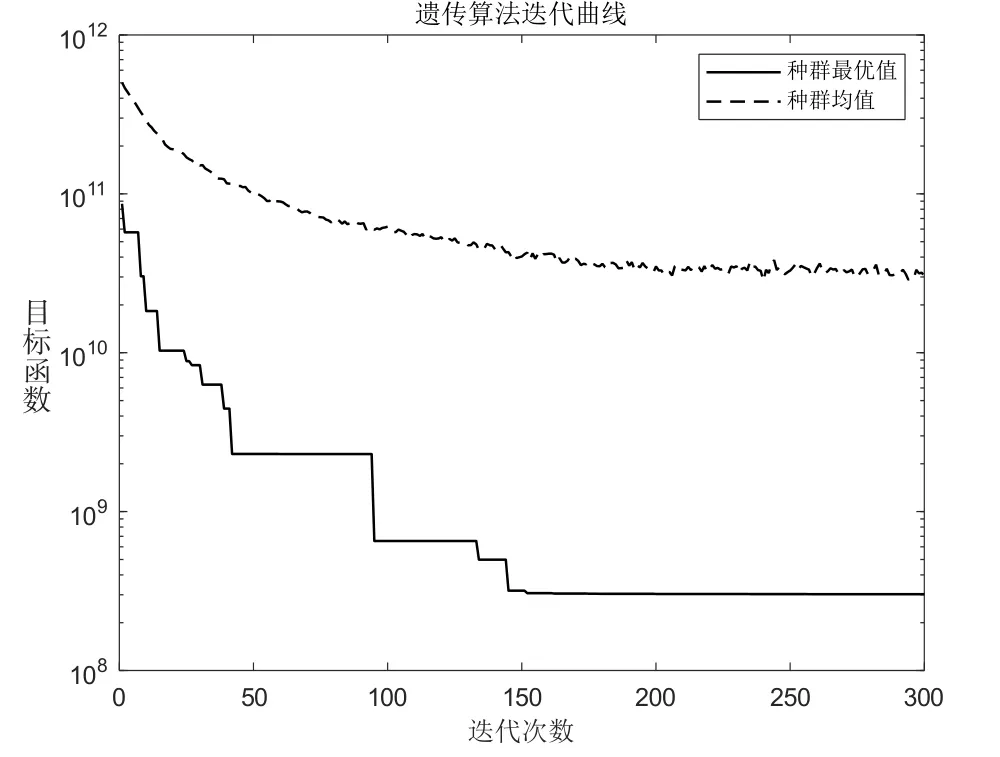
图2 最优配流方案时算法收敛曲线图