夹持式末端执行器在水果采摘中的可行性研究
杜帅


摘 要:针对目前国内水果采摘机械化程度低、采摘困难等问题,该文对现有的夹持式末端执行器应用于水果采摘中的可行性进行研究。首先,通过建立夹持水果枝干的静力学模型,推导了一种夹持力计算公式。然后,借助ANSYS对末端执行器进行有限元分析,确定了典型夹指应力和应变最大值,可针对不同采摘对象对末端执行器的材质和强度进行调整。最后,利用Adams软件建立虚拟样机模型,验证了夹持式末端执行器在水果采摘中的合理性和可行性,为进一步研究水果机械化采摘提供了技术支持和理论依据。
关键词:末端执行器;水果采摘;静力学模型;ANSYS有限元分析
中图分类号:TP24 文献标志码:A
0 引言
目前,国内水果采摘多采用人工采摘的方式,机械化程度低、采摘难度大。近几年人们开始研究借助末端执行器采摘水果。由于末端执行器夹持果实表面的夹持力大小不好控制,且容易造成果实损伤,因此如何无损采收成为机械化采收果实的一个技术难点。如果将末端执行器夹持水果表面改为夹持水果母枝,就能减少夹持力的控制难度,而夹持稳定性和夹持力的大小就成为衡量夹持机构性能的重要指标。该文从末端执行器和母枝之间的夹持力关系入手,建立两者的静力学模型,推导出一种适用于末端执行器和水果母枝的夹持力计算方法。然后通过ANSYS有限元分析确定末端执行器的夹持应力和应变量大小,以适应不同夹持对象。最后借助Adams运动学仿真,验证末端执行器应用于水果采摘中的可行性和合理性。
1 末端执行器结构原理
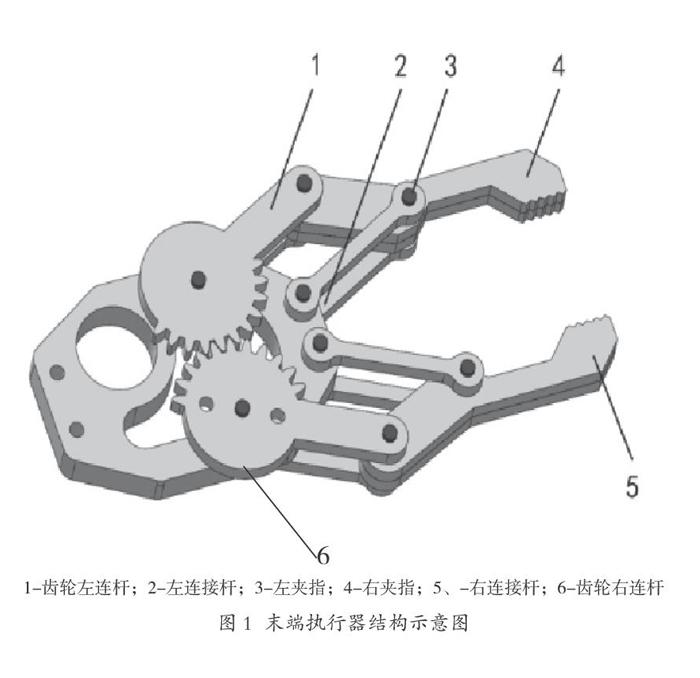
夹持式末端执行器为双四连杆结构,通过驱动齿轮连杆向中间运动,连杆带动左右夹指同时向中间运动,最终完成夾指的夹持动作[1]。其中,左右夹指的末端设计成“V”型结构,利于水果母枝嵌入其中,其夹角为2α。末端执行器结构如图1所示。
2 夹持静力学模型
2.1 夹持力封闭性分析
末端执行器夹指的夹持位置和夹持角度直接影响夹持力的封闭性。因此将水果母枝截面简化成圆形,左右夹指“V”型面对接形成的菱形轮廓与母枝的接触点为4个,可以根据多指抓取的力封闭条件判断该模型是否符合力封闭性[2]。
如图2所示,A1、A2、A3、A4分别为左夹指和右夹指与母枝的接触点。n11和n12,n21和n22,n31和n32,n41和n42分别为A1、A2、A3、A4接触点摩擦锥的矢量,S为矢量交集区域,o为夹持力矢量交点,β为接触点摩擦锥角。
由图2可以看出夹持力矢量的交点位于摩擦锥角的交集区域内,满足夹持力封闭条件,末端执行器夹持水果母枝时比较平稳。
2.2 夹持静力学分析
末端执行器夹持母枝的静力学模型如图3所示。以夹持方向为X轴,垂直于夹指夹持方向的为Y轴,母枝轴向为Z轴,建立如图3所示的坐标系。其中A和B为夹指与母枝的接触点。由于在实际的采摘过程中,会产生干扰因素,比如自然风会影响模型的受力,该文假定末端执行器在采摘水果过程中会遇到垂直于夹持方向的干扰力,即Y轴负方向的Fd,如图3(b)所示。
当末端执行器夹指完全夹住母枝时,可以完成采摘。根据夹持静力学模型,分别过A、B两点做垂直于YOZ面的旋转轴,对两点建立力矩方程
(1)
式中:d—2个接触点之间的距离;L1—干扰点与Y轴的距离;G—夹持对象重力;L2—同一夹指上下接触点的间距;θ—夹指边缘夹角;FBy、FBz—B点在Y、Z方向的压力分量;FAy、FAz—A点在Y、Z方向的压力分量;Fd—采摘过程中干扰力;FNy—夹指抵抗扰动产生的压紧力。
解得
夹指预紧力
夹指A侧正压力
夹指预紧力FB在x方向上的分力
正压力FR在x方向上的分力
当采摘对象受到干扰力Fd时,夹指所提供的的夹持力
通过静力学模型推导出的夹持力计算公式,可以应用于以后采摘末端执行器驱动力计算与驱动元件的选型中。该计算方法适用于多种夹持模型。
3 末端执行器仿真分析与验证
末端执行器在完成夹持母枝动作时,除了要考虑所需要的夹持力大小,还要考虑末端执行器前端本身的材料特性和夹持能力。为分析末端执行器在夹持母枝时本身所产生的应力和应变量,该文借助ANSYS的Workbench模块对末端执行器完成夹持动作时所产生的应力和应变进行分析,并通过Adams虚拟样机验证其夹持动作的合理性。
3.1 末端执行器有限元分析
3.1.1 建立有限元模型
在有限元分析中,为保证仿真结果的真实性和可靠性,需要将大的模型划分为许多细小的单元进行分析[3]。要尽可能地将网格画小一些,提高仿真分析的真实度。对末端执行器进行网格划分,建立的有限元模型如图4所示。考虑到末端执行器在夹持母枝时的真实情况,在夹持住母枝的一瞬间,末端执行器没有运动,因此将其合并成一个整体来分析,只在夹指的末端施加载荷。分析末端执行器在夹持母枝时各部位的应力和应变大小。
3.1.2 仿真结果分析
该文选择的末端执行器材料为6061铝合金,具有轻便、加工性能好、韧性高的特点。具体施加载荷情况可以根据夹持对象,通过夹持力计算公式计算出所需的夹持力,然后在有限元分析中对夹持部位施加相同的载荷,分析应力和应变情况。通过仿真结果可以分析末端执行器材质的选择是否合适,以及应力集中点是否需要加强材料强度。设置材料属性为铝合金,将典型荔枝采摘夹持力15 N作为载荷,以此来分析末端执行器的应变和各部分的应力情况,其应力云图和应变云图如图5(a)、图5(b)所示。
通过图5(a)应力云图可以看出末端执行器左右夹指的受力最大,其最大应力为13.6 MPa,同时左右连杆和齿轮连杆的齿轮啮合处所受应力也比较大。这些部位在以后的实际应用中应该进行加固处理,或者增强材料特性。通过图5(b)可以分析出左右夹指指端的应变量最大,然后由指端向中间递减,齿轮连杆的前端应变量最小。其夹指指端的最大应变量可以达到0.019 mm,这个应变量的大小跟选用的材质有很大关系,6061铝合金具有韧性高的特点。由于夹持对象为水果的母枝,因此应尽量选择韧性高一点的材质,在保持合理夹持力的同时也会减少对母枝的破坏,做到无损采摘。
通过对末端执行器应力和应变云图的分析,可以为以后末端执行器的设计提供一定的理论支持,尤其是在材质选择和夹指强度设计上。
3.2 末端执行器运动学仿真
3.2.1 建立虚拟样机模型
借助Adams虚拟样机可以分析末端执行器运动的平顺性和合理性,判定该结构是否在采摘工作中存在干涉问题[4]。将SolidWorks模型另存为parasolid(*.X_T)格式,导入Adams中进行质量属性等的设置。由于模型导入后为了方便运算,需要将部分零件进行布尔加运算。给末端执行器关节部位添加旋转副,非动作部位添加固定副。确保各部分之间有着约束又不影响相对运动。添加完的约束模型如图6所示。在虚拟样机中对齿轮连杆添加正反2个方向的驱动,并通过设置时间(time)和步长(step)实现夹指的夹持和松开动作。
3.2.2 仿真结果分析
在虚拟样机模型中标记夹指前端,并在后处理模块导出该部位的速度、角速度以及位置曲线,如图7(a)和图7(b)所示。
通过图7(a)速度、角速度时间曲线图可以看出,末端执行器在虚拟样机中运行比较平稳,没有出现大的波动。从图7(b)位置时间曲线图中的也可以看出,其基本与假定的夹指运动轨迹一样,能够平稳完成母枝的夹持动作。进一步验证了末端执行器运用于水果采摘中的合理性与可行性。
4 结论
该文对夹持式末端执行器应用于水果采摘中的可行性进行了分析,推导了一种夹持力的计算方法,借助有限元分析确定了该结构应力和应变最大的部位,为末端执行器以后的设计和改进提供了理论基础。最后通过Admas虚拟样机验证了末端执行器在完成夹持动作时的连贯性和平顺性。通过以上分析可以看出,该末端执行器应用于水果采摘中是切实可行的,具有一定的合理性和可行性。
参考文献
[1]赵玲亚,王英健,赵子开.圆形水果采摘机械手运动学分析与仿真[J].中国农机化学报,2020,41(3):24-29.
[2]叶敏,邹湘军,杨洲,等.荔枝采摘机器人拟人指受力分析与夹持试验[J].农业机械学报,2015,46(9):1-8.
[3]宋和义,王雷,胡聪,等.架管机的机械手爪优化分析[J].矿山机械,2020,48(4):59-62.
[4]劉佩森,靳杏子,郑翔鹏,等.基于ADAMS的工业机器人建模与动力学仿真[J].成都工业学院学报,2018,21(4):10-13,59.

