球面透视投影的鱼眼镜头全景图拼接
姜幸俭,李霆
(五邑大学,江门 529000)
0 引言
全景图是一种在各方向上全视角展示周围物理空间样貌的图像,图像拼接技术将多张具有重叠区域的图像合成大画幅、广视角的全景图,是计算机图像图形处理研究中的热点领域。全景图广泛应用于基于图像的3D场景建模和绘制[1]。
文献[2]将图像拼接流程概括为两个主要步骤,第一步:图像的配准和扭曲;第二步:寻找拼接缝隙并提供平滑的过渡。在标准镜头的情况下,文献[3]采用SIFT特征点结合RANSAC筛选同一平面特征点计算多组单应性矩阵,通过缝隙误差最小来选择合适的单应性矩阵,将单应性矩阵的方法用于生成全景图的情况中,无法避免累积误差的问题。针对鱼眼镜头,文献[4]先将鱼眼图像转换到纵向压缩的柱面投影下,然后计算单应性矩阵拼接全景图像,并且在漫游系统中展示,该方法中使用了Bundle adjustment平摊累积误差到每个镜头[5],但单应性矩阵引入的累积误差并没有消除,在漫游系统中可以看到首尾两张鱼眼图像完全没有重叠。文献[6]对双鱼眼镜头的三星Gear设备提出了一种两步配准方法,首先将鱼眼图像通过等距直角投影模型映射,手动选取匹配特征点,对匹配点求解仿射变换,评估归一化互相关参数求最优拼接参数。现有的商业软件,例如PTGUI在计算全景图时,对不同镜头采用相同的参数,并不符合实际的镜头模型。
最佳拼接缝隙的寻找是图像拼接中重要的环节,文献[7]使用动态规划的方法寻找重叠区域的拼接缝隙解决了相邻图像重叠区域存在运动物体的问题,但该方法易陷入局部最优。文献[8]在待拼接图像上以图像梯度建立无向图用网络最大流图切割寻找拼接缝隙,在消除鬼影和重影任务上取得了很好的效果。
图像融合主要有三种方法:线性融合、多分辨率融合、基于光流的方法[9]也被使用在图像拼接中。线性融合算法实时性好,但对存在的鬼影和重叠现象消除效果不明显。多分辨率方法能够消除小的拼接缝隙、且对两张照片的过渡处理效果好,但复杂度高,需要时间长。光流法计算每一个像素周围匹配的像素,消除拼接缝隙效果是最好,但容易出现形变,且计算时间长。
综上所述,针对鱼眼镜头生成全景图过程中不同镜头采用相同参数进行优化有重影的问题,本文拟采用镜头参数单独优化方法进行解决。
1 全局几何参数优化
一张高质量拼接全景图像应具备以下两个条件[10]:①几何结构上,拼接原图像对应点周围几何结构最相似。②颜色强度上,每个像素周围区域颜色过渡均匀。
1.1 映射多项式建立
从鱼眼镜头的像素坐标系映射到单位球坐标系下映射关系如图1所示。
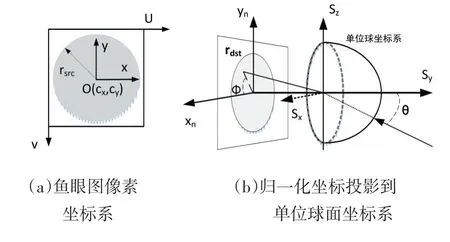
图1 像素坐标系到单位球坐标系
通过相邻图像之间的匹配特征点计算鱼眼图像的全局几何变换参数。鱼眼图像到全景图的映射方式主要有两种:正向映射,从鱼眼图映射到全景图像上;反向映射,从全景图坐标计算鱼眼图像坐标。在图像拼接映射过程中,为了避免全景图像素的缺失,默认采用反向映射方式,但在鱼眼镜头参数计算过程中采用正向映射的方式来进行特征点映射。
下面建立鱼眼镜头像素坐标系与单位球面坐标系的映射关系。根据图1(a)将鱼眼图像素坐标系(u,v)归一化到相机坐标系(xn,yn)。
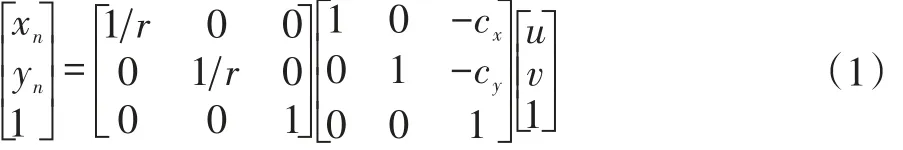
式(1)中( )cx,cy为鱼眼镜头主点像素坐标,r为鱼眼图有效像素半径。
考虑镜头在生产过程中由于生产精度或装配误差,导致鱼眼镜头成像没有严格按照投影模型。引入径向畸变多项式拟合误差如公式(2)。为了保持图像的均匀性,仅保留b和d项,并且让畸变系数之和为1保证原图像不会在映射过程中出现缩放而损失图像信息。
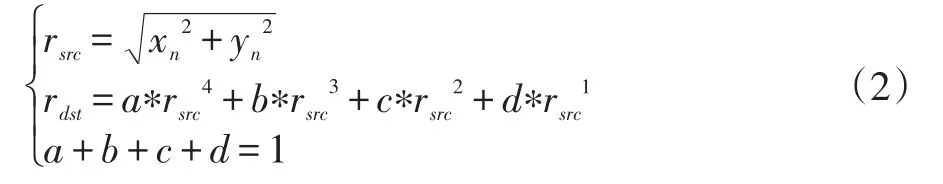
式(2)中rsrc表示鱼眼镜头相机坐标系的实际坐标,rdst为理想坐标值。
根据图2(b),可以看出光线从半球面经过折射投射到传感器平面上,根据视场角关系计算出当前像素的入射角,从而将鱼眼图上的像素映射到单位球面上。用θ表示入射角,φ表示y轴坐标与x轴的夹角,可以计算出单位球面坐标( )Sx,Sy,Sz。

式(3)中,鱼眼镜头的视场角(Field Of View,FOV),入射角θ的范围是[0 ,π] ,y轴与x轴夹角φ的范围是[-π,π]。球面坐标采用右手坐标系。
此时已经将单张鱼眼图映射到单位球上,想要获取一个完全没有视差的图像需要保持不同镜头之间光心处于同一个位置上,但在实际情况中这个条件难以满足,所以不同相机之间存在一个相对的外参矩阵,由旋转矩阵和平移矩阵构成,本文在假设相机之间光心重合的条件下进行计算,所以不同镜头之间只有旋转矩阵,没有平移矩阵。使用欧拉角旋转规范,θxθyθz分别为沿着对应轴旋转的角度,将每个镜头旋转到真实的镜头方向。
1.2 鱼眼镜头参数的优化
以上公式建立了从鱼眼图像素坐标映射到单位球坐标系下的多项式,将相邻图像匹配点对映射到单位球上,取匹配点对的球面中值作为优化目标,以中值和匹配点之间的欧氏距离作为目标函数进行优化,单独优化每个镜头的参数。如公式(4)。
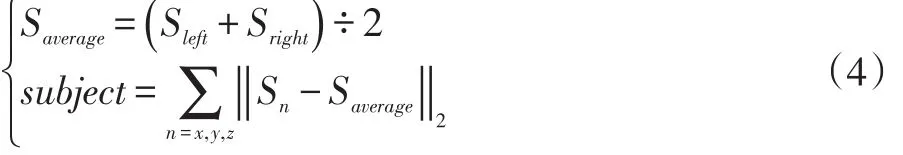
经过上述映射变换之后,通过优化公式(4)可以得到每个镜头在几何结构上最优的参数。原始鱼眼图像经过全局几何变换之后,得到一个初步的全局配准图像,但在相邻图像重叠区域由于光心不一致等问题仍会存在局部瑕疵。
2 最佳缝合线的计算和融合
2.1 最佳缝合线的计算
依次寻找有序的全景图序列S1,S2,…Sn之间重叠部分的缝合线。将相邻两张全景图映射为一张带权无向图表示图G中全部像素的集合,作为图的顶点,E表示图G中连接像素的边的集合。建立图割问题寻找最佳的拼接缝隙,代价函数表示为公式(5),图割问题具体求解方式不在本文讨论范围之内,仅设计求解方程。
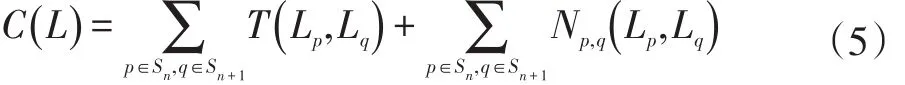
为了获得颜色上的相似性,以相邻图像相同位置颜色的欧氏距离作为边的大小。根据式(6)计算差值图。
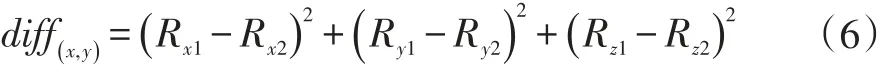
相邻两张全景图像相同位置像素的有效性可以分为三种情况:都有效、半有效以及都无效,如图2所示。
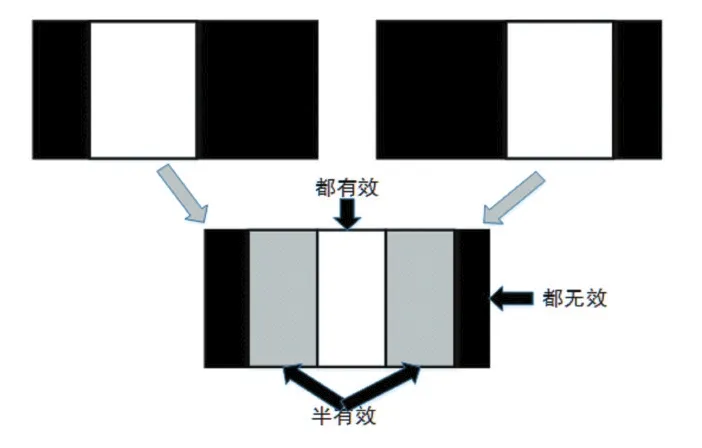
图2 相邻全景图的像素有效性
根据式(7),第一项建立每个像素顶点和终端顶点的连接T-link。根据像素在原始图像的有效性可以分为两种情况。

第二项建立相邻顶点之间边的连接惩罚项。

至此,建立了相邻图像寻找最佳缝隙的代价函数。使用文献[11]最大流方法对方程求解,可得到颜色上最相近的拼接缝隙。
2.2 多分辨率融合
在获得最佳拼接参数和拼接缝隙之后,对相邻全景图依次进行融合拼接[12]。由于不同镜头之间会存在曝光差异,采用多分辨率融合,保证过渡处的自然,并且该方法能处理拼接缝隙处细小的结构误差存在。多分辨率拼接的具体步骤如下:
Step1对待融合相邻全景图像根据拼接缝隙生成每张图像的mask图像。再根据全景图尺寸生成一张存储最终结果图的result图像。
Step2假设金字塔层数为L,对待融合全景图做L层的拉普拉斯金字塔,对应的mask做L层的高斯金字塔,此时每层mask金字塔的像素值为待融合全景图每层的权值,此外结果图也做L层的高斯金字塔。
Step3根据融合权值mask金字塔的大小将待融合全景图累加到每层的result层上,获得待重构的result拉普拉斯金字塔。
Step4从结果图拉普拉斯金字塔恢复出原尺寸大小的最终融合图。
3 实验结果分析
实验设备使用四个鱼眼镜头,正方形排列,每个镜头约200度视场角。由图3可以看出,镜头光心没有重叠,一定存在视差。

图3 实验使用设备
待优化变量为镜头像素坐标中心(Cx,Cy)、视场角FOV、畸变系数b。对比实验选取特征丰富的场景,在相同匹配特征点的情况下,对比不同镜头相同参数和不同参数下的拼接结果。

表1 多镜头统一参数优化结果
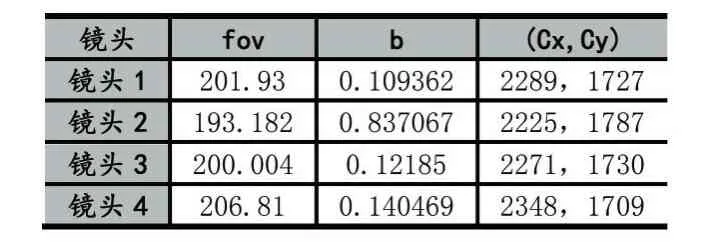
表2 多镜头独立参数优化结果
表1和表2是同样的镜头,在同一组特征点下,统一参数和独立参数的优化结果。

图4 不同镜头采用相同参数时拼接结果

图5 采用不同镜头参数时拼接结果
对比图4、图5,图4是对不同的4个镜头采用相同的参数进行优化得到的结果,图中红框部分是不同镜头重叠区域的拼接缝隙,根据下方细节图可以明显看出,在重叠区域并不能完全对齐,在每条拼接缝隙处都存在一定程度的错切。在图5的相同位置没有错切问题。
4 结语
针对鱼眼图片拼接成全景图过程中,多镜头参数优化的时,对不同镜头采用相同的参数,改进为单独优化每个镜头的参数。鱼眼图像全局几何变换之后使用图割法寻找最佳缝合线生成全景图像,最后使用多分辨率融合获得一张无缝隙的全景图像。本文的方法通用性较强,适用于各种鱼眼镜头合成全景图像。实验证明,此方法在多镜头不同参数情况下,能够获得更好的结果。
对于鱼眼图像上特征点的提取及匹配是未来主要工作方向,现有的特征点匹配方法直接从鱼眼图像上只能获取极少正确的匹配点对。

