以可视化助力儿童思维发展
王蓓

数学教学的任务是发展儿童的数学思维,提升儿童的思维品质。可视化学习让抽象的数学知识具象化,让隐性的思维显性化,是发展儿童思维能力最有效的学习方式之一。
人教版数学五年级上册第六单元的“三角形的面积”,是在学生已经掌握了三角形的特征,以及长方形和平行四边形面积公式基础上进行教学的,重点是引导学生在探索三角形面积公式的过程中,通过对图形特点的观察与分析,有意识地培养其空间想象力,渗透转化的数学思想。在本课教学中,我借助可视化教学,从学习素材、操作过程、探究思路、研究成果四个方面引领学生有效参与学习,助力思维发展。
一、学习素材的可视化,助力思维起步
在学习“三角形的面积”之前,学生已经学会了把没有学过的图形通过“剪拼”的方法,转化成已经学过的图形,来研究它的面积。但教材呈现的是用两个完全相同的三角形进行拼组,即“倍拼”的方法研究。从“剪拼”到“倍拼”,学生思维有一个大跨越,课堂上如果教师只是简单给予学生两个三角形让他们去拼,学生只能是机械操作,不知其所以然,失去了探究的意义。因此,教师要精准把握学生的思维起点,以学定教,让知识的形成过程更加合理、自然。基于以上思考,我精心设计了如下的前置性作业,让学生课前先学。
【教学思考】
学生虽然对三角形十分熟悉,但如果让他们自行探究面积公式,不少学生会束手无策。因此,我以学生十分熟悉的直角三角形为切入点,引导他们自主探究方格图上直角三角形的面积,学生依据生活经验,发现直角三角形的面积是它所在的长方形面积的一半,很自然地唤醒学生的学习经验,为后续研究一般三角形面积埋下伏笔。
将直角三角形置于方格图这一背景中,实际上就是把面积探究的素材可视化,它具备两大优点:一是借助方格图让三角形的面积可数。方格图让抽象的面积具象化,可以直接数出所包含的面积单位。方格图还利于学生发现三角形和与它等底等高的长方形之间的联系,自然而然发现他们面积之间的关系。二是借助方格图让动手操作更便捷。学生在想一想、画一画、算一算的过程中充分调动眼、脑、手多感官合作,从而不断尝试多角度探究直角三角形的转化路径,以画促思。
二、操作过程的可视化,助力思维碰撞
由于学生个体的差异性以及已有知识储备不一,学生对探究材料的学习会呈现出个性化思考。教学中,我基于学生的思维起点,由浅入深地展示可视化学习成果,引领学生在读懂他人作品的同时进行思维互补,从而完善个人的认知结构。
【教学片段】
师:老师这儿搜集了几份前置作业,我们一起来看看吧!
出示第一份作业:
生:我是用数方格的方法来求的。满格的有8个,不满格的也有8个,两个不满格的可以合成一个满格,所以直角三角形的面积是8+8÷2=12(cm2)。
师:通过数方格的方法,数出满格和不满格的数量就能计算出直角三角形的面积。
出示第二份作业:
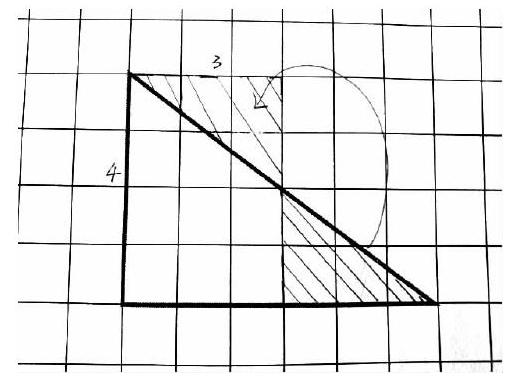
生1(指图):我是把下面阴影部分的三角形剪下来,再拼到上面,这样就把直角三角形转化成了一个长方形。因为长方形的长是4cm,宽是3cm,面积是4×3=12(cm2),所以直角三角形的面积就是12cm2。
师:谁有问题和他交流?
生2:请问3是怎么来的?
生1(指图):这条长的直角边是6cm,我从它中间这里剪开,6÷2=3(cm)。
师(追问):不从中间剪能转化成长方形吗?
生1:不行。
师:从这剪开行吗?这儿呢?(指到除中点外任意一点)如果沿着中点剪呢?
课件演示“剪拼法”。
师:看来,运用剪拼的方法能将直角三角形转化成我们学过的长方形,再根据长方形面积进行计算,这种方法非常巧妙!瞧,我们班上还有高手!
出示第三份作业:
师:谁看懂他的方法了?
生1:他是在原来直角三角形上面添补了一个直角三角形,就转化成一个长方形。长方形面积是24cm2再除以2就得到直角三角形面积。
师:补的这个三角形有什么特点?
生2:和原来的一样。
师:你怎么知道一样呢?
生2(指图):因为长方形对边相等,补上去的三角形两条直角边也是4cm和6cm。
师:你观察得真仔细!
展示第四份作品:
(不出声)
学生恍然大悟
【教学思考】
学生在研究直角三角形面积时呈现出三种不同的思维水平,其中“数方格”是基础,“剪拼”是学生已有经验的有效迁移,“倍拼”是学生已有认知经验的“变式”。无论是剪拼还是倍拼,都是要把三角形面积转化为已知平面图形的面积来解决问题。
实际中,“剪拼”是有一定难度的,因为剪拼须找到三角形的中位线(学生还未触及)。因此,在帮助学生理解“剪拼”法時,我以学生的质疑“3从哪里来?”为突破口,引导学生想象非中位线剪无法拼组的过程,接着展示沿中位线剪拼成功的过程,通过前后对比,学生对“怎么剪拼、为什么剪拼”有了初步的感知。
相对而言“倍拼”就显得简单多了。被可视化的学生作品就是一种无声思维,它向学生传递着“为什么要倍拼、怎么倍拼”的数学信息。学生借助可视化的作品理解他人的思考过程变得简单多了。数学思维也在看一看、想一想、说一说等活动中碰撞、内化、发展。
三、探究思路的可视化,助力思维发展
学生在研究直角三角形面积计算时已经积累了较为丰富的数学活动经验,初步感悟“剪拼”“倍拼”两种转化的思想方法。运用这些方法,学生在探究一般三角形面积时就能够触类旁通,举一反三。
【教学片段】
师:直角三角形面积能转化成长方形和平行四边形来计算,任意一个三角形都能转化成我们学过的图形吗?请拿出准备好的探究材料在小组里操作验证。
探究材料:每个小组颜色不同的3个锐角三角形或3个钝角三角形,剪刀一把;其中1号和2号三角形完全一样。
小组合作后汇报:
组1(演示):我们将1号和2号两个锐角三角形拼成了一个平行四边形,3号和1、2号都拼不成。
教师板贴学生倍拼后的作品。
组2(演示):我们组1号和2号两个钝角三角形也拼成了一个平行四边形,3号和1、2号都拼不成。
师:老师很奇怪,3号为什么总是拼不成呢?(同时呈现三个三角形)
生:3号和它们不是一样大。
师:你怎么知道的?
生(演示):我可以将3号和1号重叠在一起,发现它们的边不相等。如果把1号和2号重叠在一起,发现它们能够重合。
师:“重合”这个词用得非常好!当两个三角形能够完全重合时,我们就说它们“完全一样”(板书)。两个完全一样的三角形一定能拼成什么图形?
生:平行四边形。
师:还有不一样的转化方法吗?
组3(演示):我们组用的是剪拼法。先找到锐角三角形两条边中点的连线,再沿着这条线剪下一个三角形,将它拼到下面梯形的边上,这样就拼成了一个平行四边形。
教师将学生剪拼后的作品板贴
……
【教学思考】
心理学家皮亚杰认为“儿童的智慧源于操作”。有效的可视化操作活动不但能够激发学生的学习兴趣,还能让学生在操作中经历、体验。课堂上,我给学生充分的时间剪、拼、展示、交流,引导他们在三个三角形的操作比较中感悟关键词“完全一样”,在“剪拼”和“倍拼”具体操作过程中感受转化的策略,进而得出结论:无论怎样的三角形,只要两个完全相同一定能拼成一个平行四边形,从而发现三角形的面积是它拼成的平行四边形面积的一半。无论怎样的三角形,只要沿着两条边中点的连线剪开,一定能拼成一个平行四边形,从而感知三角形的面积和转化后的平行四边形面积相等。
由特殊的直角三角形到普通的三角形,可视化操作让每一位学生在多角度操作验证中获得真实有效的体验,直观感知了图形的转化过程,积累了丰富的基本数学活动经验,学生的思维变得更加灵活、深刻。
四、研究成果的可視化,助力思维进阶
三角形转化为平行四边形后,学生的探究不能嘎然而止,建立并运用三角形面积公式的模型才是本课教学的知识目标。为此,在课堂上引领学生有效观察拼成的平行四边形,自主推导三角形的面积公式,形成完善的三角面积公式的模型。
【教学片段】
出示探究要求:
1.选择一个你喜欢的图形(转化后的图形)进行研究。
2.仔细观察转化后的平行四边形与原三角形,你有什么发现?
3.你能推导出三角形面积公式吗?
学生自主探究后汇报。
生(指图):我选择的是“倍拼法”后的图形。我发现转化后平行四边形的底就是原三角形的底,平行四边形的高是三角形的高,原三角形面积等于平行四边形面积的一半,所以,三角形面积=底×高÷2。
师:谁听明白了?
生1、2……
师:转化过程中什么变了?什么没变?
生:底和高都没有变,面积变了。三角形的面积只有平行四边形面积的一半。
师:所以三角形面积=平行四边形面积÷2=底×高÷2。谁研究了“剪拼法”后的图形?
生(指图):我发现转化后平行四边形的底等于原三角形的底,平行四边形的高等于原三角形的高的一半,也就是高÷2。平行四边形的面积等于底乘高,所以三角形面积=底×高÷2。
师:你们听明白了吗?
生1、2……
师:在这个变化过程中什么变了?什么没变呢?
生(指图):三角形面积没有变,底也没有变,高变小了,只有原来高的一半。
得出结论:三角形面积=底×高÷2,用字母表示为S=ah÷2。
【教学思考】
学生在计算三角形面积时经常漏了除以2,究其原因,是在三角形面积公式推导过程中学生没有深刻理解除以2的根本原因。用“倍拼法”来推导面积公式,学生能够比较轻松地发现三角形与拼成的平行四边形在底和高的长度、面积方面的变化,进而得出结论。而用“剪拼法”来推导面积公式,学生发现三角形和拼成的平行四边形面积和底都不变,平行四边形的高只有原三角形高的一半,所以三角形面积要除以2。
教学中,学生两次经历观察、比较、推理、抽象等学习过程,在“变与不变”的思维历程中建模、用模,让数学学习真正发生,学生抽象思维能力得到有效的发展。

