基于因子模型的流动性对资产定价的影响研究
欧阳红兵 喻静琼
摘 要:流动性是资产定价研究领域的重要议题。本文通过沪深A股2000年7月至2018年6月的个股数据,用换手率与Amihud指标测度流动性,运用Fama-MacBeth截面回归与构造投资组合进行时间序列回归的方法,比较两个指标作为流动性测度的实证表现,构造流动性因子建立我国股市流动性扩展的六因子模型。研究结果表明,我国股市存在流动性溢价;换手率比Amihud指标更适合作为我国股市的流动性定价指标;换手率测度流动性水平构建流动性扩展的六因子模型对我国股票市场收益特征的解释是有益的。
关键词:因子模型;流动性;换手率;Amihud指标
中图分类号:F830 文献标识码:A 文章编号:1674-2265(2020)07-0013-10
DOI:10.19647/j.cnki.37-1462/f.2020.07.002
一、引言
自1990年末上海和深圳证券交易所先后建立以来,我国证券市场经过近30年的发展,不断壮大日渐完善,已形成包括主板、中小企业板、创业板和科创板等多层次的证券市场体系。根据上海和深圳证券交易所统计,截至2019年12月31日,上海证券交易所挂牌股票1629只(其中主板A股1499只,主板B股50只,科创板80只),市值总价346734.79亿元;深圳证券交易所股票2242只(其中主板A股461只,主板B股47只,中小板943只,创业板791只),上市公司总市值达237414.86亿元。我国股票市场整体上获得了长足发展,投资者数量也相当庞大,但与发达国家股票市场相比依然不够成熟,特别是在投资者结构方面。我国股市投资者中机构投资者比重小,散户占比很高,而散户投资者远没有机构投资者成熟理性,对冲风险的手段也相对较少,过度投机情况严重。散户投资者容易跟风引发羊群效应,而大量机构投资者也热衷于追涨杀跌,市场极易出现暴涨暴跌的现象。与此同时,我国股市也存在着高换手率特征。
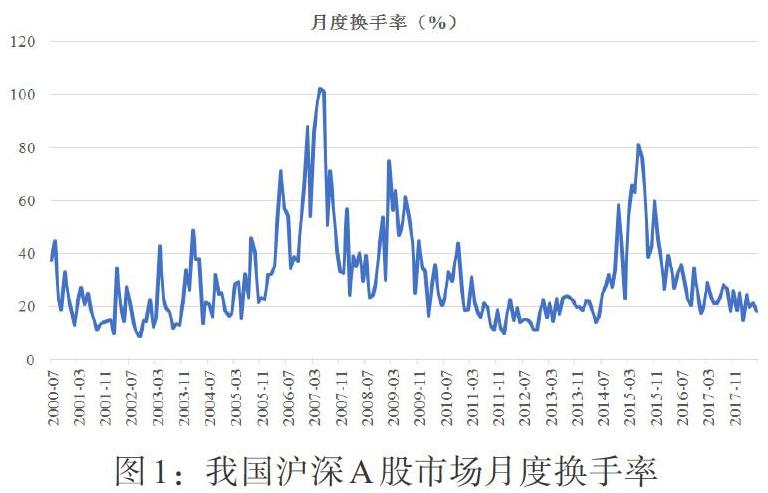
图1为我国沪深A股市场2000年7月至2018年6月的换手率水平,可以看到换手率水平整体在30%左右,在股市行情较好的情况下甚至达到100%, 高换手率水平一方面意味着流动性水平高,市场交易活跃,投资者热情高涨;另一方面也代表市场上短期投资行为较普遍,价值投资意识不强,投机性强。因此,关注流动性水平,理解流动性与资产定价的关系,有助于提醒投资者理性投资,维护自身利益。
关注市场系统流动性需要着眼于交易资产的流动性与资产定价的关系。Amihud等(2013)[1]在系统阐释流动性与金融危机之间的关系时就曾指出,理解流动性(流动性水平)以及流动性风险同资产定价的关系是理解金融危机的核心。本文研究流动性对股票收益率的影响,通过换手率与Amihud指标测度我国个股与投资组合的流动性水平,构造流动性定价因子,在Fama-French五因子模型的基础上建立包含流动性因子的资产定价模型。
二、文献回顾
(一)流动性定义与测度
流动性是证券市场活力的体现,其确切含义在学术界尚未达成一致定论。目前学术界较广为接受的是从宽度、深度、弹性和及时性这四方面来定义流动性(Kyle,1985;Massimb和Phelps,1994;靳云汇和杨文,2002;Sarr和Lybek,2019)[2,3,4,5],宽度主要指交易在短期内得到执行所需要的成本,深度指不会影响当前交易价格的交易量,弹性指交易价格从波动状态恢复到均衡的速度,及时性指以合理价格执行交易的时间。流动性的含义是多维的,对流动性的度量也需从多方面考虑,不能仅刻画流动性某一方面的特征。
使用交易价格来衡量流动性的主要有Roll指标(Roll,1984)[6] 、实现价差(Harris,1990)[7]以及市场效率系数(MEC)(Hasbrouck,1991)[8]。使用交易量测度流动性最常用的指标是换手率,特别是在研究我国股市流动性问题时(苏冬蔚和麦元勋,2004;梁丽珍和孔东民,2008;陶希晋和勾东宁,2010;熊家财和苏冬蔚,2013)[9,10,11,12],也有直接使用交易量(陈辉和顾乃康,2017)[13]来衡量流动性。将价格与交易量相结合来测度流动性的指标比较多,而且运用也相当广泛。Martin(1975)[14]通过每日价格变化幅度的平方与每日交易量的比值来衡量流动性,即Martin 流 动 性 比 率。Dubofsy和Groth(1984)[15]提出Amivest流动性比率,用资产价格变化每1个百分点时需要多少交易量的变动来测算,该流动性指标最先由 Amivest 公司使用,后来成为纳斯达克市场衡量流动性的指标之一。Marsh和Rock(1986)[16]提出Marsh-Rock 流動性比率,采用特定时间内的交易数量来度量流动性水平。Amihud(2002)[17]提出Amihud非流动性指标,该指标是流动性水平的负向指标,即Amihud非流动性指标值越大,代表流动性水平越低。Pástor和Stambaugh(2003)[18]提出Gamma系数来测度流动性,简称P-S流动性指标。
(二)流动性与资产定价
在资产定价模型不断发展完善的大背景下,流动性在资产定价理论与实证研究中也逐渐得到重视。
较早开始研究流动性与资产定价关系的是Amihud和Mendelson(1986)[19],他们用买卖价差测度非流动性水平,实证发现美国股票市场个股预期收益率与非流动性存在正相关关系,且预期收益率是非流动性指标的凹函数。Datar等(1998)[20]用换手率测度流动性水平,研究发现在控制相关变量后流动性对期望收益的影响依然显著,而且影响作用并不是只存在于一月份。Acharya和Pedersen(2005)[21]将流动性(流动性风险)视作一个定价因素,将其加入资本资产定价模型(CAPM)中,通过均衡分析推导出流动性调整的资本资产定价模型(LCAPM)。Chan和Faff(2005)[22]通过澳大利亚股票市场1990—1998年的月度数据,在Fama-French三因子模型的基础上用换手率测度流动性,研究流动性的资产定价作用,研究证明加入流动性的因子模型是稳健的。Liu(2006)[23]通过实证研究发现,美国股票市场存在CAPM模型与Fama-French三因子模型无法解释的流动性溢价,于是在传统CAPM模型的基础上用投资组合模拟法构造流动性因子并将其加入CAPM模型中得到流动性扩展的资本资产定价模型(LACAPM)。Amihud等(2015)[24]用其提出的Amihud非流动性指标构造了流动性因子IML,并通过全球45个股票市场数据进行实证研究,发现流动性溢价在全球股票市场普遍存在。Moshirian等(2017)[25]通过全球39个证券市场数据进行实证研究,结果表明个股流动性与市场流动性的协动性在全球大多数股票市场中是已被定价的,且在发达国家证券市场中的定价效应更强。
国外学者在这方面的研究起步较早,理论与实证研究都比较丰富,国内学者更多的是运用国外学者的理论对中国股市进行实证研究。陈青和李子白(2008)[26]在CAPM模型的基础上,借鉴并改进了Liu(2006)[23]的方法,构造出新的流动性因子,构建我国股市流动性调整的CAPM模型(CCAPM)。刘峰和霍德明(2012)[27]研究发现在Fama-French三因子的基础上引入流动性因子可以明显降低GRS检验统计值,提高模型对投资组合收益率的拟合效果。韩金晓和吴卫星(2017)[28]使用股票交易最高价和最低价来度量流动性,并以Amihud非流动性指标为参照,发现股票收益的流动性溢价现象普遍存在于各股票市场,并且换手率比价差类指标在度量中国股票市场流动性时更有效。李艳茹(2018)[29]基于沪深两市全部A股数据在Fama-French五因子模型基础上考虑流动性因素, 研究结果表明我国股票市场定价模型基本符合包括市场风险、规模效应、流动性效应和价值效应所确定的四因子模型,流动性因素对于定价模型具有显著的改善作用。石广平等(2019)[30]运用MS-AR模型研究市场流动性与资产价格的非线性关系时发现市场非流动性对股票、债券等资产的当期价格均存在正向影响。
综上所述,流动性测度指标非常之多,各种不同的流动性度量指标在实证中优劣表现并不一致,综合考虑价格与交易量的指标对流动性测度比较全面,既体现流动性宽度与深度特征又考虑到交易量对价格的影响。在流动性与资产定价理论与实证研究中,大部分研究都证明流动性对资产横截面收益(价格)与时序收益(价格)都存在显著影响,无论是国外市场还是我国股市都存在流动性溢价。本文基于理性定价的原则,结合各指标对我国股市流动性情况的适用性,选择换手率和Amihud非流动性指标(后文将该指标取负数改为正向的流动性测度指标)作为我国A股市场股票流动性水平的衡量指标。在实证研究方法上,Fama-MacBeth截面回归是研究影响资产价格横截面差异因素的经典方法,对股票进行分组,通过投资组合构建因子并进行时间序列回归则是Fama-French类因子模型的精髓。本文通过Fama-MacBeth截面回归和构造投资组合进行时间序列回归作为主要实证方法,在Fama-French五因子模型的基础上构建我国股市流动性扩展的六因子模型。
三、实证设计
本文借鉴Liu(2006)[23]在传统资产定价模型中加入新因子的思想,以Fama-French五因子模型为基础,通过换手率和Amihud指标测度流动性构造流动性因子加入五因子模型中,建立流动性扩展的因子定价模型。
按照Fama和French(2015)[31]采用2×3投资组合划分方法以流通市值加权平均构造流动性因子。为方便表述,将换手率衡量的流动性对应的因子称为换手率流动性因子,记为[TLiq],将Amihud指标衡量的流动性对应的因子称为Amihud流动性因子,记为[ALiq]。按公司规模大小将股票分成规模小组([S])和规模大组([B]),然后分别对每组按照换手率从低到高分成3组,低([TL])、中([TN])、高([TH])组分别占比30%、40%和30%,由此得到6组投资组合([STL],[STN],[STH],[BTL],[BTN],[BTH])。采用同样的方法对规模和Amihud指标排序分组得到6组投资组合([SAL],[SAN],[SAH],[BAL],[BAN],[BAH])。再根据如下计算方法即可得到换手率流动性因子([TLiq])和Amihud流动性因子([ALiq])。
[STH]表示规模小组([S])且换手率高([TH])的投资组合,其他符号意义类推[TLiq]表示在考虑规模因素后换手率高的投资组合月度平均收益率与换手率低的投资组合月度平均收益率之差。[ALiq]表示在考虑规模因素后Amihud指标值高的投资组合月度平均收益率与Amihud指标低的投资组合月度平均收益率之差。
得到各因子变量后将两组流动性因子分别加入原来的Fama-French五因子中,得到本文主要研究的两组六因子模型:
模型(1)和(2)中的[Rit]表示资产在t时期的收益率,[Rft]表示无风险利率,[Rmt-Rft]表示市场风险溢价因子(即市场超额收益率,是考虑现金红利再投资的月市场收益率与月度化无风险利率之差所得),系数为b;[SMBt]表示规模因子,系数为s;[HMLt]表示賬面市值比因子,系数为h;[RMWt]表示盈利因子,系数为r;[CMAt]表示投资因子,系数为c;模型(1)中的[TLiqt]表示通过换手率测度的流动性因子,其系数记为[i1];模型(2)中的[ALiqt]表示通过Amihud指标衡量的流动性因子,其系数记为[i2];[αt]和[et]分别表示截距与残差项。
分别构建5×5规模—换手率组合(Size-Turnover)与规模—Amihud组合(Size-Amihud),用投资组合收益序列对五因子模型与两组六因子模型进行时间序列回归,检验各因子模型能否对流动性溢价做出较好解释。采用同样的5×5投资组合构造法构建规模—账面市值比组合(Size-BM)、规模—盈利组合(Size-OP)和规模—投资组合(Size-Inv),用这3种特征的投资组合对五因子模型和两组六因子模型进行回归,并将两组流动性扩展的因子模型与五因子模型的回归结果进行比较,检验流动性扩展的六因子模型在解释我国股市规模效应、账面市值比效应、盈利效应与投资效应上的实证表现。最后通过Gibbons等(1989)[32]提出的GRS检验对两组六因子模型对组合收益率的拟合效果进行检验,并与五因子模型进行比较,对模型做出总体评价。
四、实证分析
(一)数据选取与变量定义
本文选择沪深A股(包括主板、创业板和科创板)作为实证研究对象,样本期为2000年7月1日至2018年6月30日,原始数据均来自国泰安(CSMAR)金融数据库。个股月度与日度数据包括考虑现金红利再投资的收益率、交易金额、交易股数和流通市值,剔除交易状态为ST和PT以及收益率空缺的数据。市场收益率数据为沪深A股市场考虑现金红利再投资的综合月(日)度市场收益率。月(日)度无风险利率为定期整存整取年利率根据复利计算方法将年度利率月(日)度化所得。个股对应的公司财务数据为1998—2017年的半年与年度数据。Fama-French五因子数据为2000年7月至2018年6月的月度数据。
个股超额收益率用考虑现金红利与再投资的个股收益率减去无风险利率所得。换手率(Turnover)通过交易股数与流通股数的比值来计算所得。原本的Amihud指标是非流动性测度指标,本文为了直接反映流动性,对该指标取负对数值,因此在本文实证研究中Amihud指标值越大代表流动性越好,是正向的流动性指标,通过个股日度数据计算出月度Amihud指标,具体计算公式如下:
其中,[Ni,t]表示第t月股票i的交易天数,[|Ri,d,t|]表示股票i在第t月第d日的收益率绝对值,[Voli,t,d]表示股票i在第t月第d日的交易额。市场风险(β)用CAPM模型中的β系数衡量,在每个月将个股的日度超额收益率数据对市场超额收益率(考虑现金红利再投资的日度市场收益率减去日度无风险利率)数据回归所得。公司规模(Size)采用第t年6月底的流通市值来衡量第t年7月到第t+1年6月的公司规模。账面市值比(BM)用第t-1年年末的每股净资产除以流通股股价计算所得。盈利能力(OP)用t-1年年末的每股营业利润除以每股净资产计算所得。投资水平(Inv)用t-1年年末的资产增长率来衡量,即用第t-1年的资产与第t-2年的资产之差再除以第t-2年的资产计算所得。
(二)换手率与Amihud组合的当期收益特征
将每个月的个股数据按照换手率或Amihud指标从低到高排序分成样本大小相等的10组,依次为L,2,3,…,H,L表示最低,H表示最高。根据流通市值加权计算各组合的当期超额收益率,组合的规模为组合内个股流通市值的加总再除以组内股票个数,然后对月数(2000年7月至2018年6月一共216个月)取平均值。
先看换手率组合的收益特征。随着股票组合的换手率越来越高,超额收益率呈现单调增大趋势,且换手率水平最高的组合与最低的组合超额收益率之差超过6%。换手率越高,代表流动性水平越高,对组合当期收益率有正向影响,可以初步判断我国股市存在流动性溢价。另外,组合的规模随着换手率水平的变大而单调减小。
再看Amihud组合的收益特征。除去Amihud指标最低的股票组合外,组合的当期收益率隨着Amihud指标增大而增大。Amihud指标值越大,组合的流动性越好,因此对股票组合当期收益率整体上的正向影响也可判断出我国股市存在流动性溢价。同时,Amihud指标越大的股票组合,规模也越大,这一点与换手率组合的表现是相反的。
(三)横截面预期收益率影响因素分析
Fama-Macbeth回归模型中的因变量均为预期超额收益率,将Fama-French五因子模型中的变量作为控制变量,检验换手率与Amihud指标对股票截面预期收益率的影响显著性水平。
将换手率组的回归(1)(3)(5)分别和Amihud指标组的回归(2)(4)(6)比较起来看,换手率的系数值也比Amihud指标系数值大,说明换手率对预期收益率的影响更大。各控制变量在两组模型中的表现也存在明显差异。与Amihud指标组的变量系数相比,市场风险系数(β)在换手率组中显著性与符号不变,系数值略大;公司规模(Size)在两组中的表现差异最大,在换手率组中为负但不显著,在Amihud指标组的回归中在1%的水平上显著为负,且系数值也很大(相对于其他变量系数值)。账面市值比的系数在换手率组中比Amihud指标组中略大(0.018,0.009)。盈利能力在换手率组的回归(5)中没有在Amihud指标组的回归(6)中显著,符号由正变负。投资水平在两组模型中均不显著。比较两组模型截面回归的平均R2,可以发现回归(1)比(2)大,回归(3)比(4)大,回归(5)比(6)大,换手率组的整体拟合效果比Amihud指标组好。
Fama-Macbeth截面回归结果说明,换手率与Amihud指标对我国股票横截面预期收益率都存在显著影响。将市场风险系数、公司规模、账面市值比、盈利能力与投资水平作为控制变量后,换手率稀释了其他变量对预期收益率的影响,而Amihud指标对收益率的影响作用在加入控制变量前后的差异并不明显,说明换手率比Amihud指标对股票截面预期收益率的解释能力更强。
(四)新模型对流动性溢价的解释能力分析
在对因子模型进行时间序列回归前检验各因子变量间的相关性水平。
从各因子之间的相关系数可以看出,规模因子与账面市值比因子、盈利因子、两个流动性因子均存在较高的相关度,盈利因子与投资因子、两个流动性因子也存在较高的相关度,相关系数超过了0.5。然而两个流动性因子之间的相关系数绝对值却不足0.1,说明两个指标所包含的信息是存在明显差异的。整体上换手率流动性因子TLiq与五因子的相关系数值小于Amihud流动性因子ALiq与五因子的相关系数值,说明六因子模型(1)的变量相关性水平比模型(2)低。
为排除各因子变量间的相关性导致时间序列回归存在多重共线性问题,在用各因子模型对投资组合回归时使用VIF方差膨胀因子来判断。经检验,各因子变量的VIF值都小于5,五因子变量VIF的平均值为2.83,六因子模型(1)中因子变量VIF平均值为2.76,略小于六因子模型(2)VIF的平均值(3.07)。由此说明各因子模型都不存在严重的多重共线性。
为了检验两组六因子模型对流动性溢价的实证表现,本文用规模—换手率组合的超额收益率序列分别对五因子模型与六因子模型(1)回归,用规模—Amihud投资组合的收益率序列对五因子模型与六因子模型(2)回归,通过与五因子模型的回归结果比较,判断两组六因子模型对资产收益率的解释能力是否更进一步。
比较回归截距项可以发现,五因子模型25组回归中只有8个不显著,六因子模型(1)中不显著的有11个,说明整体上六因子模型对规模—换手率组合的回归表现更好。再看六因子模型(1)回归中各因子变量的表现,市场风险因子25个系数全是显著的,规模因子只有1个不显著,且随着规模增大,规模因子系数在逐渐变小,至规模最大时各换手率水平上的规模因子都变成负的;账面市值比因子与盈利因子都只有少数几个系数在10%和5%的水平上显著,投资因子的系数不显著的有9个,换手率流动性因子(TLiq)在换手率处于第二低的水平下有3个不显著,其余的都比较显著,在换手率水平最低时(L),流动性因子系数为负值,随着换手率水平变高各规模组的流动性因子系数在变大,到换手率水平最高且规模最大时流动性因子系数接近于1。各变量系数说明,在对规模—换手率组合的解释上,六因子模型(1)中除账面市值比因子与盈利因子外,其他因子的表现都很好,且六因子模型(1)比五因子模型对规模—换手率组合的拟合效果更好。
25组回归中五因子模型截距项不显著的有10个,六因子模型(2)中不显著的有19个,只有2个是在1%的水平下显著,说明六因子模型(2)对规模—Amihud组合的解释力非常强,表现明显优于五因子模型。市场风险因子全都显著,规模因子有22个显著,且随着规模越来越大规模因子的系数在变小至规模最大组系数变成负值;账面市值比因子、盈利因子与投资因子都只有3个左右的系数在1%水平上显著;Amihud流动性因子(ALiq)主要是Amihud指标处于第三水平时不显著,有19个都在1%的水平下显著,随着Amihud指标越来越大,流动性因子系数也越来越大。在对规模—Amihud组合收益率的拟合上,六因子模型(2)主要通过市场风险因子、规模因子和流动性因子(ALiq)起到解释作用,账面市值比因子、盈利因子与投资因子并不显著。
六因子模型(1)对规模—换手率投资组合的拟合效果比五因子模型好,六因子模型(2)对规模—Amihud投资组合的拟合效果也比五因子模型好,说明流动性扩展的六因子模型对我国A股市场流动性溢价效应的解释能力优于五因子模型。
(五)两组流动性因子比较分析
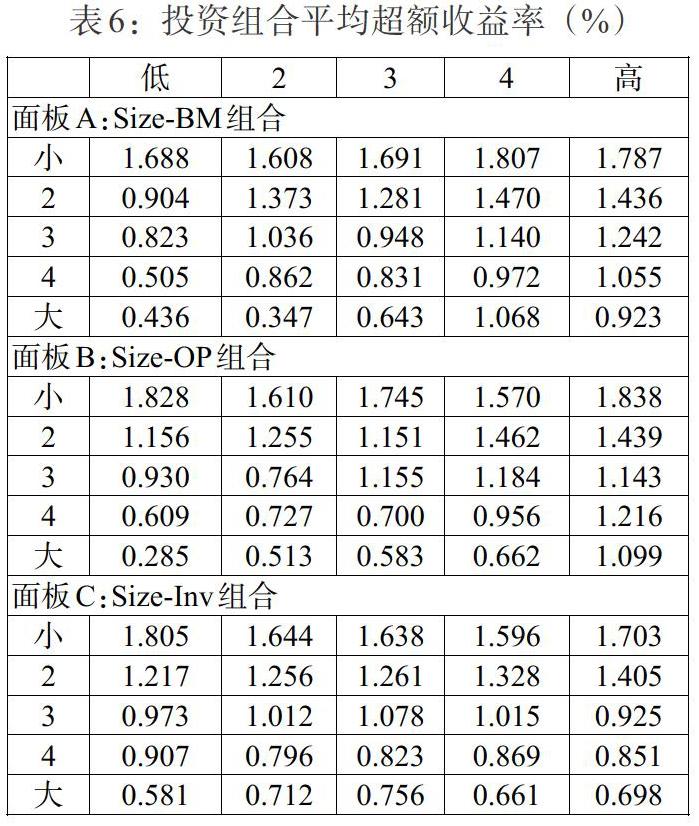
为了比较两组流动性扩展的六因子模型对相同投资组合拟合表现,本文通过规模—账面市值比组合(Size-BM)、规模—盈利组合(Size-OP)与规模—投资组合(Size-Inv)收益序列分别对两组六因子模型回归,比较两组流动性因子在模型中的表现。各投资组合的216个月的平均收益率见表6。
在规模—账面市值比(Size-BM)投资组合中,组合的超额收益率整体上表现出随着账面市值比的增高而增大,5组不同规模大小的最高账面市值比组合的收益率都比最低账面市值比组合的收益率高,证明我国股市存在账面市值比效应,即账面市值比越高收益率越高;5组高低不同的账面市值比组合中,收益率都是随着组合的规模变大超额收益率变小,在规模—盈利組合(Size-OP)和规模—投资组合(Size-Inv)中这一特征也表现得非常明显,因此可以判定我国股市存在显著的规模效应,即规模越小收益率越高。在规模—盈利(Size-OP)组合中,盈利能力与收益率的关系不是单调的递增或递减,整体上盈利能力水平越高,组合的超额收益率越高,盈利能力最高的组合比盈利能力最低的组合收益率高,这与Fama和French的研究中美国股市表现的特征一致,而与部分国内学者对我国股市实证研究的结果相反。在规模—投资(Size-Inv)组合中,投资水平与收益率的正负关系并不明显。
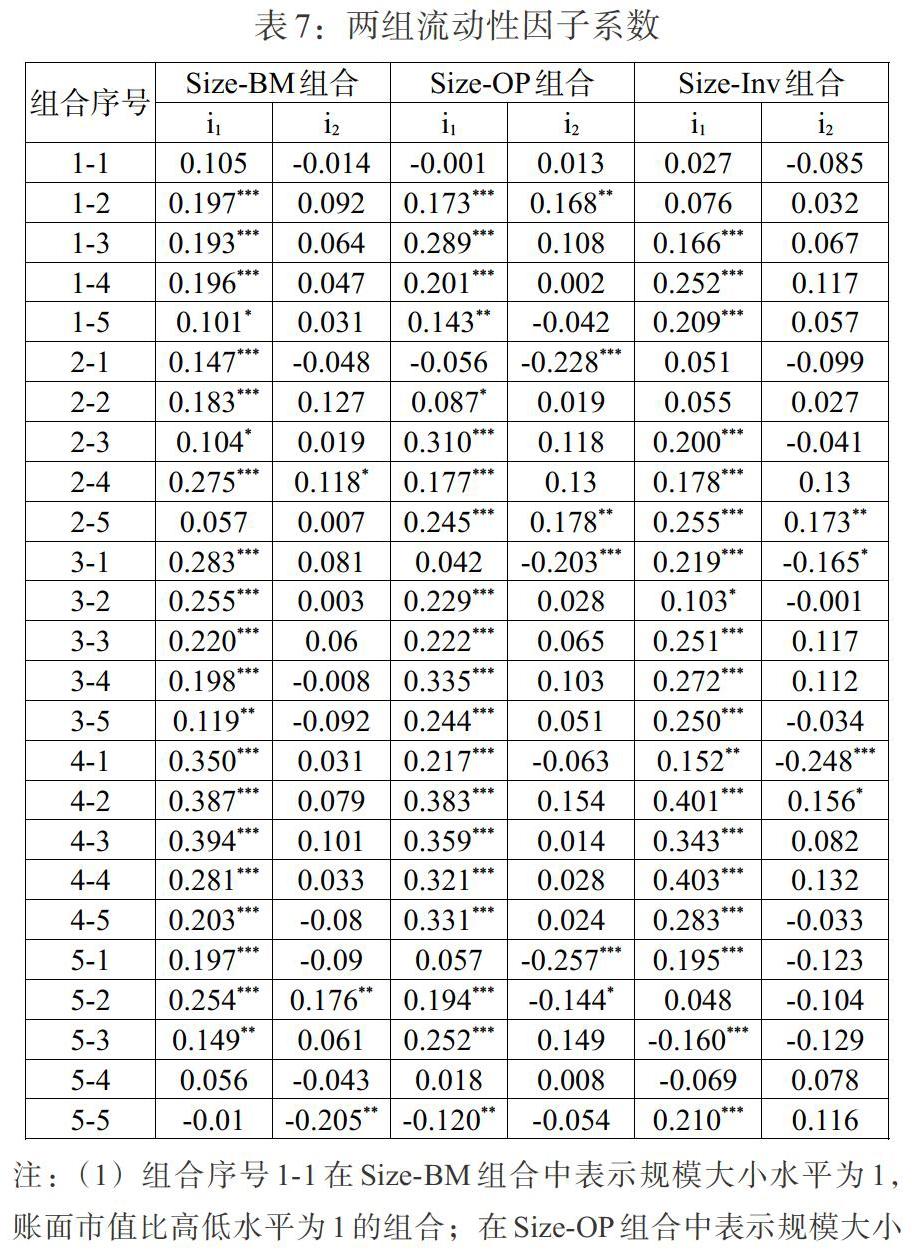
两组流动性因子在模型回归中的表现如表8,i1为六因子模型(1)中换手率流动性因子的系数,i2为六因子模型(2)中Amihud流动性因子的系数。
两组六因子模型的流动性因子表现存在明显的差别,六因子模型(1)对应的换手率流动性因子(TLiq)在三种特征的投资组合回归中,几乎都是显著的,只有少数几个系数不显著,在规模—账面市值比组合只有4个不显著,在规模—盈利组合中5个不显著,在规模—投资组合中6个不显著;而六因子模型(2)对应的Amihud流动性因子(ALiq)在三种特征的投资组合回归中均只有3个左右的系数显著,绝大多数系数都不显著。两组流动性因子的表现说明以换手率衡量的流动性因子的引入有助于解释我国A股市场的规模效应、账面市值比效应、盈利效应与投资效应,而Amihud指标测度的流动性因子对这三种特征投资组合收益率的解释没有明显的边际作用。
为了将六因子模型(1)与模型(2)同时和五因子模型进行对比,本文用规模—账面市值比组合(Size-BM)、规模—盈利组合(Size-OP)与规模—投资组合(Size-Inv)的时间收益序列分别对五因子模型和两组六因子模型回归(受篇幅所限回归结果细节未列出)。三组模型对各投资组合回归的截距项表现不一致,但六因子模型(1)调整后的R2在三种投资特征组合回归中都是最高的。
(六)GRS检验与总体评价
为了对两组六因子模型对投资组合的拟合效果进行总体评价,本文参照Fama和French(2015a)[31]的做法,使用Gibbons等(1989)[32]提出的GRS检验将两组流动性因子模型与五因子模型回归拟合效果进行对比分析。GRS检验以模型所有回归的截距项是否同时为零作为原假设,GRS值越小,其p值越大(一般以p值等于0.05作为判断界线),接受截距项联合为零原假设的可能性越高,模型的拟合效果也就越好;A|α|表示所有回归截距项绝对值的平均值,代表回归中收益率不能被因子变量解释的部分,值越小表明模型被解释的效果越好,A(R2)为所有回归调整的拟合优度系数的平均值,值越大代表模型的拟合优度越高。
六因子模型(1)的GRS值小于五因子模型,A|α|小于五因子模型,A(R2)大于五因子模型,说明六因子模型(1)对规模—换手率投资组合的拟合效果明显比五因子模型好。六因子模型(2)的GRS指标小于五因子模型,A(R2)大于五因子模型,二者的A|α|值几乎没有差别,同样证明六因子模型(2)对规模—Amihud投资组合的拟合效果优于五因子模型。GRS检验结果说明两组流动性扩展的六因子模型对流动性溢价特征的拟合表现比五因子模型更好。
在规模—账面市值比(Size-BM)组合的拟合中,六因子模型(1)的GRS值比六因子模型(2)和五因子模型的都要小,说明对账面市值效应的解释上六因子模型(1)比六因子模型(2)和五因子模型更具说服力;五因子模型对规模—盈利(Size-OP)组合和规模—投资(Size-Inv)组合的GRS值比两组六因子模型小,说明在解释我国A股股市收益率的盈利效应和投资效应上,五因子模型比六因子模型更有优势;在面板A、B、C中,六因子模型(1)的GRS值都比六因子模型(2)的GRS值小,说明以换手率测度流动性的六因子模型比Amihud测度流动性的六因子模型对规模效应、账面市值比效应、盈利效应与投资效应等特征解释能力更强。
三组模型总体拟合效果说明,流动性扩展的六因子模型比五因子模型对我国股市流动性溢价特征的解释能力强;六因子模型(1)比六因子模型(2)更具普适性,在我国A股市场的实证表现更稳健;六因子模型(1)与五因子相比,在解释我国股市规模效应、账面市值比效应以及流动性效应上具有优势,但在解释盈利效应与投资效应上不如五因子模型。因此用换手率作为流动性代理指标,通过规模与换手率排序构造流动性因子,建立流动性扩展的六因子模型可以在一定程度上提高因子模型对我国A股收益特征的拟合效果。
五、结论
流动性在我国股票市场发展中起着至关重要的作用,是资产定价研究领域不可忽视的主题之一。本文通过沪深A股2000年7月至2018年6月的个股收益与财务数据,将换手率与Amihud指标作为流动性的代理指标,主要运用Fama-MacBeth截面回归与投资组合时间序列回归的方法,实证研究两个指标作为流动性测度在因子定价模型中的表现,尝试构建流动性扩展的六因子模型。
研究结果表明:(1)换手率和Amihud指标都与当期收益率存在正相关,与预期收益率负相关,但换手率比Amihud指标对个股收益率的解释能力更强。(2)无论是用换手率还是Amihud指标测度流动性水平,都证明我国股市存在流动性溢价,即流动性水平越高(流动性风险越低),当期资产收益率越高(流动性风险补偿小),预期收益率越低。(3)用换手率和Amihud指标测度流动性水平构建流动性扩展的六因子模型比Fama-French五因子模型对我国股市流动性溢价的解释效果更好;换手率流动性因子比Amihud流动性因子对投资组合收益率拟合的边际贡献更大,包含换手率流动性因子的六因子模型比包含Amihud流动性因子的六因子模型对我国股市规模效应、账面市值比效应、盈利效应等特征的拟合效果更好。(4)包含换手率流动性因子的六因子模型在解释我国股市规模效应与账面市值比效应特征上比Fama-French五因子模型表现更优秀,但解释盈利效应与投资效应上不如五因子模型。
研究结论说明,用换手率测度流动性水平构造流动性因子并将其加入Fama-French五因子模型中建立流动性扩展的六因子模型经得起实证检验,对我国股票市场收益特征的解释是有益的,给资产定价模型进一步发展提供了可靠证据。
参考文献:
[1]Amihud Y.,Mendelson H.,Pedersen L.H. 2013. Market Liquidity:Asset Pricing,Risk,and Crises [M].New York:Cambridge University Press.
[2]Kyle A.S. 1985. Continuous Auctions and Insider.Trading [J].Econometrica,(53).
[3]Massimb M.N.,Phelps B.D. 1994. Electronic Trading,Market and Liquidity [J].Finance,(36).
[4]靳云匯,杨文.上海股市流动性影响因素实证分析 [J].金融研究,2002,(6).
[5]Sarr A.,Lybek T. Measuring Liquidity in Financial Markets [EB/OL].https: //ssrn.com/abstract=880932,2019-12-8.
[6]Roll R. 1984. A Simple Implicit Measure of the Effect Bid-ask Spread in An Efficient Market [J].Journal of Finance,39(4).
[7]Harris L.E. 1990. Statistical properties of the roll serial covariance bid/ask spread estimator [J].Journal of Finance,65(2).
[8]Hasbrouck J.,Seppi D.J. 2001. Common Factors in Prices,Order Flows,and Liquidity [J].Journal of Financial Economics,59(3).
[9]苏冬蔚,麦元勋.流动性与资产定价:基于我国股市资产换手率与预期收益的实证研究 [J].经济研究,2004,(2).
[10]梁丽珍,孔东民.中国股市的流动性指标定价研究 [J].管理科学,2008,(3).
[11]陶希晋,勾东宁.我国流动性的层次与传导机制研究——基于2005—2009年数据的实证分析 [J].安徽大学学报(哲学社会科学版),2010,34(3).
[12]熊家财,苏冬蔚.股票流动性与企业资本配置效率 [J].会计研究,2014,(11).
[13]陈辉,顾乃康.新三板做市商制度、股票流动性与证券价值 [J].金融研究,2017,(4).
[14]Martin P. 1975. Analysis of the Impact of Competitive Rates on the Liquidity of NYSE Stocks [R].Economic Staff Papers75-3,Securiites and Exchange Commission.
[15]Dubofsky A.D.,Groth J.C. 1984. Exchange Listing And Stock Liquidity [J].The Journal of Financial Research.

