基于交替条件期望变换的凝析气藏露点压力预测模型

孙博文，郭 平，伍轶鸣，汪周华，周代余，刘志良

（1.西南石油大学油气藏地质及开发工程国家重点实验室，四川成都610500；2.中国石油塔里木油田分公司勘探开发研究院，新疆库尔勒841000）

在凝析气藏衰竭开发过程中，随着温度、压力的降低，当压力低于第一露点时，原本在凝析气中以气态存在的凝析油将逐渐析出，产生的反凝析现象不仅将凝析油损失在地层中，而且会堵塞地层渗流通道，降低气井产能[1-2]。为防止反凝析现象的产生，开采时常常保持地层压力高于露点压力[3]。为此，准确测定凝析气藏露点压力，对于保障此类气藏高效开发至关重要。

近年来，国内外确定凝析气藏露点压力的方法主要有：实验法、状态方程、人工神经网络、深度学习智能模型等。凝析气藏露点压力的实验测定可根据国家标准《油气藏流体物性分析方法》[4]中的恒质膨胀（CCE）方法，实验测试虽较为准确，但其成本较高、耗时耗力。VALIOLLAHI 等[5]采用改进的Peng-Robinson（PR）状态方程进行凝析气藏露点压力计算，并与Soave- Redlich- Kwong（SRK）和Schmidt-Wenzel（SW）等状态方程进行了精度对比，但热力学模型需要进行各组分的二元系数拟合，且求解收敛性存在一定的问题。除上述方法外，许多新的理论方法也逐渐用于露点压力的预测，HAJI-SAVAMERI等[6]利用改进的径向基函数神经网络（Radical Basis Function，RBF）预测了凝析气藏露点压力，并与多层感知器（Multilayer Perceptron，MLP）算法进行对比；ZHONG 等[7]基于粒子群优化算法（Particle Swarm Optimization，PSO），采用支持向量机（Support Vector Machine，SVM）方法，构建了PSO-SVM露点压力预测模型，新发展的深度学习智能模型虽能进行复杂的非线性回归，且预测精度较高，但其和人工神经网络类似，均无法给出显式模型，且无法进行自我推理解释，矿场应用存在一定局限性。

为此，基于最优化理论和应用统计分析，提出了一种利用交替条件期望变换方法确定的凝析气藏露点压力非参数回归模型，获取了具有统计意义的露点压力显式关联式。目前，该方法已成功应用于CO2-原油最小混相压力预测[8-9]、岩石物性参数确定[10]、油井连通性定量表征[11]等方面，但尚未应用于凝析气露点压力预测。因此，在Pearson关联性分析基础上，选取气藏温度、（C1、C2-C6、C7+）摩尔分数、C7+相对分子质量、C7+相对密度作为新模型的自变量，采用公开发表的27组露点压力数据探索自变量和因变量之间的潜在函数关系，并对9组TLM油田实测露点压力数据进行预测。结果表明：模型回归的AARD为2.16%，模型预测AARD仅为4.8%，其中最大ARD为9.21%，最小ARD为0.34%。本研究为凝析气藏露点压力预测提供了一种参考方法。

1 交替条件期望变换（ACE）理论基础

在实际生产中，自变量和因变量之间的函数关系往往难以直接确定，若仅对固定的或者经验的函数形式进行模型参数回归，其预测结果往往不甚理想，普适性较差[12]。因此，引入无明确函数关系要求的非参数回归方法是十分必要的。交替条件期望变换便是一种非参数回归方法，该方法是一种估算最佳变换的多元回归方法，其变换结果是使一个因变量和多个自变量之间有最大相关系数[13]。

对于多元回归问题，ACE模型的回归形式一般为：

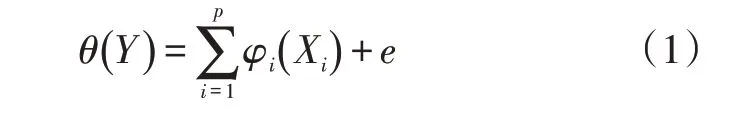
式中：θ(Y)、φi(Xi)分别为被解释变量与解释变量的期望函数；p为自变量个数；e为回归误差。

则误差的方差方程为：

因此，可以建立以误差方差为最小的目标优化函数，如式（3）所示：

式中：模型的约束条件为且

目标函数优化过程中的迭代条件为：

式中：θ*,φ*分别为被解释变量与最优解释变量；e2为误差方差。

结合式（3）—式（4），再根据式（2），建立的每个变量的单一条件期望函数为：

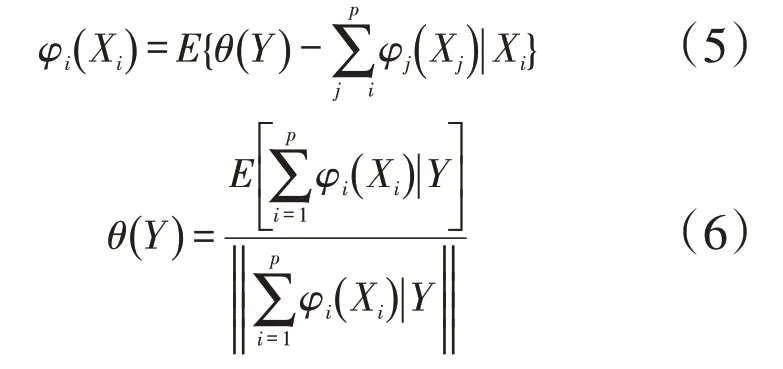
式（5）—式（6）中：j为除变量i以外的其它自变量。条件期望的计算采用随机变量的条件期望进行计算。

电力安全生产中风险随时存在，因此，做好风险管理是为了解决电力生产过程中存在的安全问题，同时，为了电力企业在生产过程中可能存在的安全事故起到防微杜渐的效果。在风险控制过程中，需进行一些科学、合理的分析，能使其在实际应用中获得更好地效果，发挥更大的价值。

则最终获取最优交替条件期望变换模型为：

2 ACE露点压力预测模型建立

2.1 数据与变量选择

选取已公开发表的27组凝析气藏露点压力数据[14]探索ACE模型中自变量和因变量之间的潜在函数关系，实验数据见表1。

如图1所示，在ACE 露点压力模型自变量的选择问题上，采用Pearson关联性分析法，探究了露点压力影响因素排序。

Pearson 相关系数法[15]是一种准确度量2个变量之间的关系密切程度的统计学方法，对于2个变量x和y，通过试验可以得到若干组数据，记为（xi,，yi），i=1，2，…，n，则Pearson相关系数的数学表达式为：

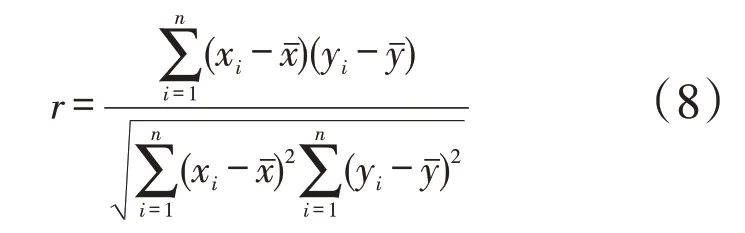
式中：xi，yi分别为2种变量的第i个数值，分别为2种变量n个试验值的均值。相关系数r的取值范围在-1和+1之间，即|r|＜1，|r|越接近1，表明x与y相关程度越高。

通过Pearson关联性分析（图1）可得，N2+CO2摩尔分数对露点压力的影响程度较低，原因在于CO2和N2属于非烃组分，与气藏重组分和中间组分相互作用较小，并且在凝析气流体中的含量一般较低，因此可忽略。故选取气藏温度、（C1、C2-C6、C7+）摩尔分数、C7+相对分子质量、C7+相对密度可作为ACE模型的输入变量。其中：气藏温度为375.15～423.77 K、（C1、C2-C6、C7+）摩尔分数分别为63.7%～95.57%、0.77%～21.52%、0.21%～11.11%，C7+相对分子质量为124～228，C7+相对密度为0.759～0.847。

表1 凝析气藏露点压力实验数据Table1 Experimental data of dew point pressure in condensate gas reservoirs

图1 凝析气藏露点压力影响因素分析Fig.1 Influencing factors analysis of dew point pressure of condensate gas reservoirs

2.2 改进模型的建立

利用上述ACE方法理论，通过表1中的27组露点压力实验数据，探索每个变量的单一条件期望函数，从而获取最佳条件期望变换模型，建立凝析气藏露点压力预测模型，自变量包括气藏温度、（C1、C2-C6、C7+）摩尔分数、C7+相对分子质量、C7+相对密度，自变量与因变量之间的最佳变换回归方程为：

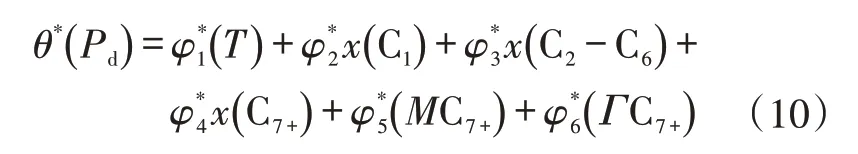
式（9）—式（10）中：Pd为露点压力，MPa；T为气藏温度，K；x（C1）为C1摩尔分数；x（C2-C6）为C2-C6摩尔分数；x（C7+）为C7+摩尔分数；M（C7+）为C7+相对分子质量；Γ（C7+）为C7+相对密度。

对式（10）作逆变换可得：

式（11）中上角标“-1”为对函数作逆变换。

由于ACE方法属于非参数回归，本身并未提供自变量和因变量变换过程的函数关系式，采用多项式对该变换过程的函数关系进行拟合（图2）。

同样作出露点压力实验数据Pd与通过最佳变换得到的Pd转换值θ*（Pd）的函数关系式（图3）。

结合各自变量的最佳变换及多项式拟合结果，以及露点压力实验数据Pd与通过最佳变换得到的Pd转换值θ*(Pd)的关系式，最终得到以下基于ACE方法的凝析气藏露点压力预测新模型，即式（12）—式（15），ACE模型回归系数如表2所示。

图2 ACE方法对各自变量的最佳变换及多项式拟合Fig.2 Optimal transformation of independent variables determined by ACE and fitted polynomials functions

图3 因变量的最佳变换及曲线拟合Fig.3 Optimal transformation of dependent variables determined by ACE and curve fitting

3 结果与分析

在2.1节凝析气藏露点压力实验数据表中，已给出了建立ACE模型时采用的27组实验数据对应的预测值（图4），模型回归的AARD为2.16%，ACE模型的预测值和实验值均匀分布在45°线附近，其中最小、最大误差分别为0.03%、5.93%。该模型的适用范围为：气藏温度为375.15～423.77 K，（C1、C2-C6、C7+）摩尔分数分别为63.7%～95.57%、0.77%～21.52%、0.21%～11.11%，C7+相对分子质量为124～228，C7+相对密度为0.759～0.847。结果表明：建立的ACE模型对解决凝析气藏露点压力问题，有良好的回归能力。但是建立模型的回归误差并不能代表模型的预测或泛化能力，为了进一步验证本文建立的露点压力模型的预测能力，选取了9组TLM油田的实测凝析气藏露点压力数据[16]，并对其用建立的ACE露点压力模型进行预测，对比结果如表3所示。其中，最大ARD为9.21%，最小ARD为0.34%，该预测集的AARD为4.80%，该模型的预测精度较高，具有较好的泛化能力。

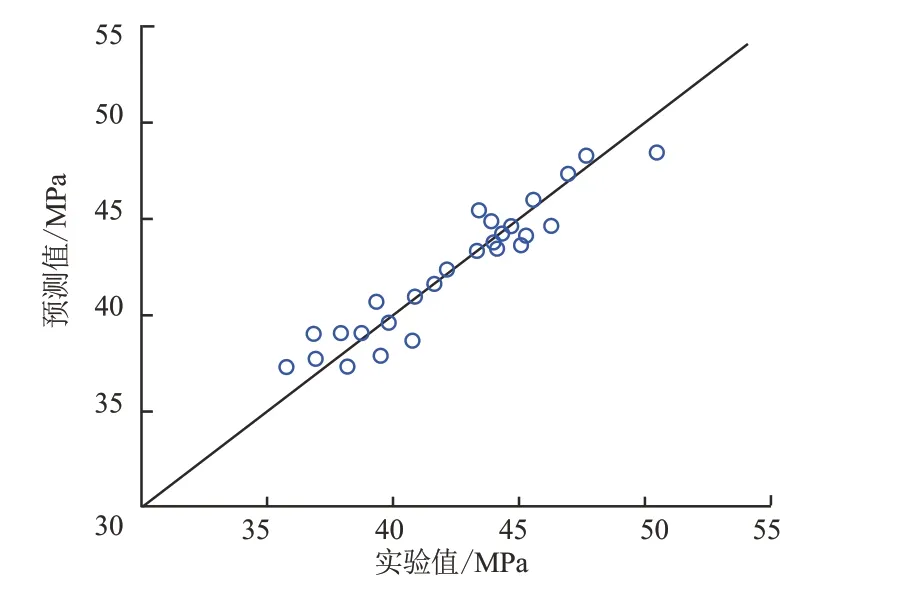
图4 ACE模型回归结果Fig.4 Regression results of ACE model

表2 ACE模型公式系数Table2 Equation coefficients of ACE Model

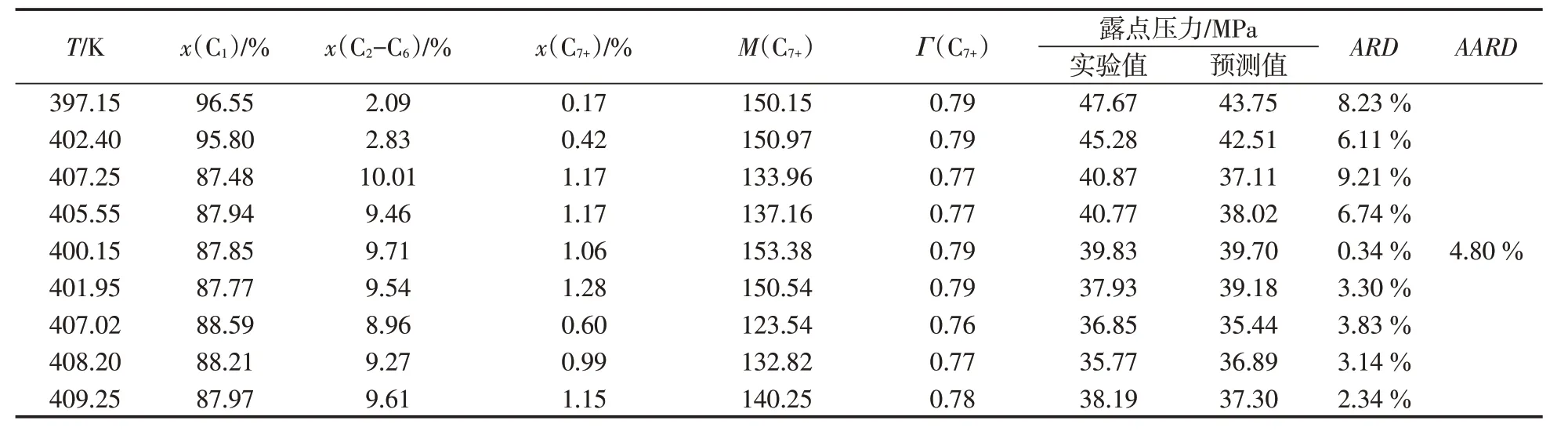
表3 非样本凝析气藏露点压力数据预测结果Table3 Prediction results of dew point pressure of condensate gas reservoirs for non-sample data

4 结论

1）基于最优化理论和应用统计分析，提出了一种利用交替条件期望变换方法确定的凝析气藏露点压力非参数回归模型，获取了具有统计意义的露点压力显式关联式。

2）根据Pearson关联性分析，探究了凝析气藏露点压力主力影响因素，最终确定模型的输入变量为：气藏温度、（C1、C2-C6、C7+）摩尔分数、C7+相对分子质量、C7+相对密度。

3）提出的模型在模型回归中的AARD为2.16%，模型预测AARD仅为4.8%，其中最大、最小ARD分别为9.21%、0.34%，精度相对较高，具有良好的泛化能力，可满足凝析气藏工程计算的需要。