考虑信号灯状态的经济车速规划
雷朝阳, 高建平,2*, 屈俊凯, 郗建国
(1. 河南科技大学车辆与交通工程学院,洛阳 471003;2. 河南科技大学机械装备先进制造河南省协同创新中心,洛阳 471003)
近年来,随着中国汽车保有量迅速增长导致能源消耗、交通堵塞及汽车行驶安全等问题日益突出,信号交叉口作为城市道路的“咽喉”,这一问题尤为严重[1]。以“节能、环保、安全”为目标的新一代汽车成为今后汽车工业发展的方向[2]。车辆受信号灯的干预频繁“停-走”,导致通行效率下降,且额外增加了车辆的行驶时间、燃油消耗及尾气排放[3]。如何在车辆到达信号交叉口前对车速进行合理控制优化,使其不停车平滑通过信号灯路段是解决上述问题的关键。
随着智能交通(intelligent transportation system,ITS)的发展,车路协同(intelligent vehicle infrastructure cooperative systems,IVICS)技术在解决道路交通拥堵、环保及安全等方面得到大量应用。在该环境下,车辆可通过通信协议[如DSRC(dedicated short range communication)、LTE(long term evolution)、Wi-Fi、5G等]与邻近车辆和道路基础设施进行信息交互[4],据此驾驶员可根据车速引导的方式合理控制车辆,以减少车辆延误和不必要的停车[5-6]。周熙阳等[7]针对不同转向类型构建信号交叉口等待时间模型,提出了考虑交叉口转向类型的A*算法的拓展算法(CMTA*)算法。但该算法假定行程时间不变,且忽略了车辆在信号交叉口处的延误,无法实际应用。孟竹等[8]通过分析车辆通过信号信号交叉口时的驾驶行为,划分6种情形,建立油耗模型估算求解得到最优生态驾驶速度轨迹;Liu等[9]根据驾驶员驾驶习惯对通过交叉口的速度进行优化,从而减低油耗,缩短等待时间;安实等[10]提出一种多级可变速度限制的信号交叉口绿色驾驶控制方法,该方法在不增加行程时间的基础上使车辆驶近信号交叉口的车速更平滑;Yang等[11]提出一种新的分布式算法,使车辆通过十字路口时保持一定的非零速度,缩短了加速过程时间;鹿应荣等[12]根据下游交叉口信号相位信息,通过自动驾驶车辆控制模型计算出车辆连续通过多个路口的恒定速度,同时为保证乘客舒适性,用平滑三角函数曲线对车速进行优化,避免了车辆在交叉口处急加/减速情况。但是该方法得到的是一个恒定车速,不能真实反映城市交通的特征。胡林等[13]通过马尔科夫链构建信号交叉口红绿灯的概率模型,在车辆近交叉口处对车速进行优化,最后通过A*算法求解最优通行车速,该方法减少了计算用时,在交通信号灯密集处优势明显。
综上所述,前人在研究连续信号交叉口车速规划时聚焦于将其看作多个单点信号交叉口的结合,并未考虑对全路段的车速进行规划,且大多以经济性为目标,忽略了因车辆受信号灯影响而造成的延误及额外增加的停车等待时间。针对此问题,提出了考虑信号灯状态的经济车速规划方法;借助车路协同技术,在车辆进入信号控制区域后,根据获取前方路口信号灯相位信息及距各个交叉口的距离,建立了车辆通行引导控制模型;对各驾驶行为下车辆时空轨迹进行分析,分别以路口停车次数及车辆延误最小为目标,对双目标协同优化,建立统一优化目标函数,利用多目标粒子群优化算法求得最优经济车速,使车辆以相对平稳的车速不停车连续通过前方各路口,实现减少停车次数及降低车辆延误,最后通过搭建的仿真平台进行方法验证。
1 问题描述及目标
车辆在城市工况行驶时经常会因红灯而被迫停车。图1为车辆连续通过多个信号交叉口的车速引导示意图。在无车速引导下,不同的驾驶员根据自身驾驶习惯不同,出现急加速/减速而造成车速差异性大,导致车辆因红灯相位被迫停车。运用车路协同技术,通过车载设备、路测设备获取车辆运行线路前方路口信号灯相位信息,建立连续路口通行经济车速引导模型,通过粒子群算法求解通过各个信号交叉口的经济引导车速,之后将建议车速提供给驾驶员参考,使驾驶员有针对性地控制车速,使车辆尽可能以一个平稳的车速通过其行驶前方连续多个信号交叉口。目标是在经济车速引导下,车辆可有效减少在信号交叉口处停车,从而节省在路口停车启动时间损失,一定程度上减少了车辆行程时间及停车次数,降低了车辆延误时间。

图1 信号交叉口车速引导示意图Fig.1 Speed guidance diagram at signalized intersection
2 车速控制系统及引导模型建立
2.1 系统框架
车路协同系统由智能路测系统、智能车载系统及无线通信系统组成[14],如图2所示。智能路测系统可将信号灯相位信息通过DSRC专用通信通道传递到监控中心,通过模型、算法优化给出当前车辆行驶最优方案;智能车载系统主要基于环境感知获取车辆行驶周围环境、车辆运行状态及车辆位置等信息,通过V2V(vehicle-to-vehicle)、V2I(vehicle-to-infrastructure)模块与其他车辆或路测设备共享,实现协同控制,从而提高车辆行驶安全性及通行效率;无线通信技术将整个系统融合一体,保证相关信息实时传递。
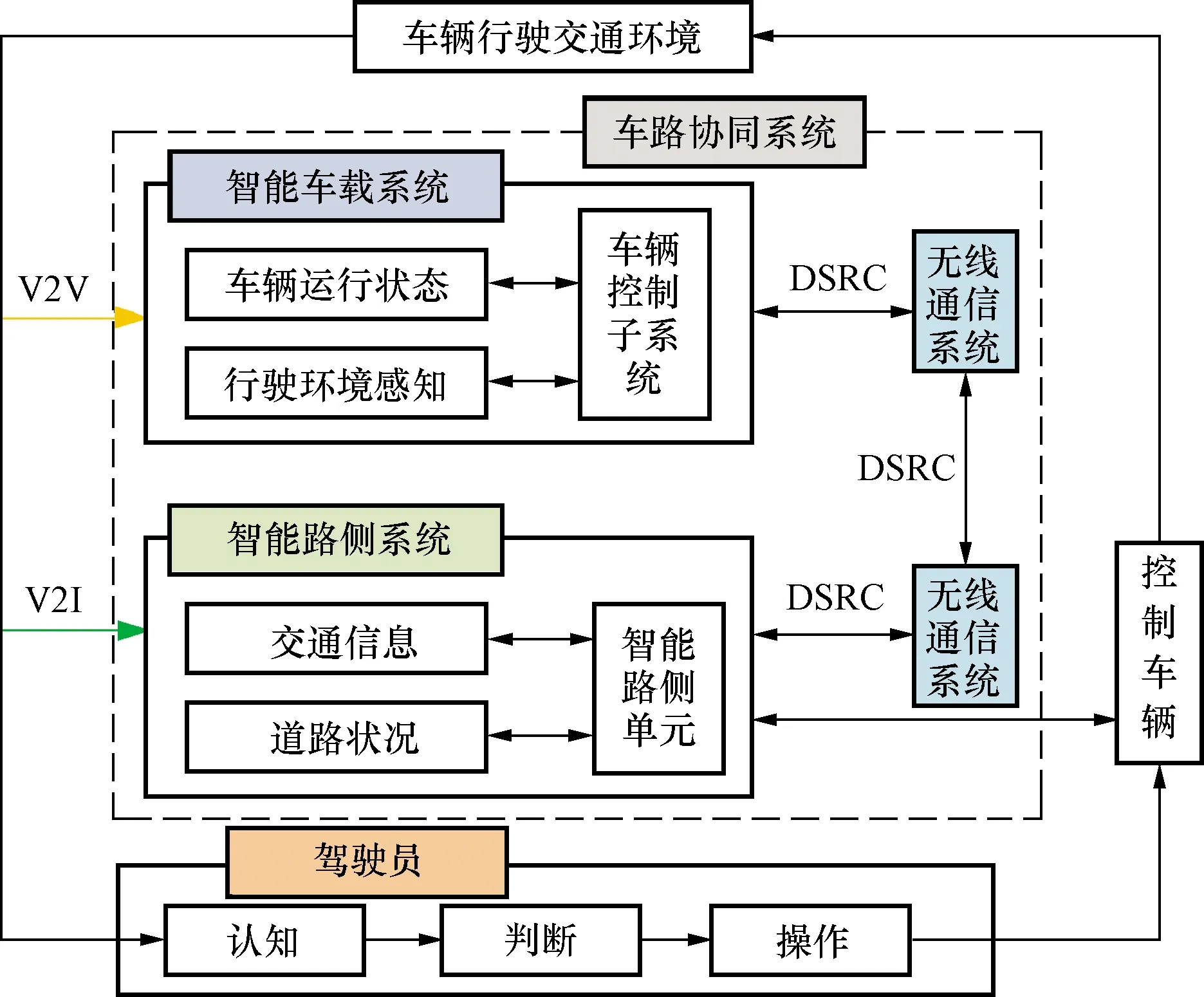
图2 车路协同系统框架示意图Fig.2 Cooperative vehicle infrastructure systerm framework
2.2 车速引导模型
2.2.1 模型基本假设
为锐化研究问题,做以下基本假设。
(1)在路测设备与车载设备进行信息交互时,通信延迟可忽略不计。
(2)驾驶员严格按照引导车速操控车辆。
(3)在场景中建立的道路坡度为零。
(4)车辆在道路上行驶时不受行人及其他交通参与者的影响。
(5)只考虑直行车道,不考虑车辆在信号交叉口处的左、右转弯。
2.2.2 基于信号灯状态的经济车速引导模型
为便于分析,将信号灯状态划分为绿灯和红灯(包含黄灯时刻),设车辆与路测设备通信范围为L=300 m;假设车辆进入通信范围时刻为t0,此时车辆初速度为v0,gij表示在第i(i为全程路段信号灯个数,下同)个信号交叉口处信号灯第j(j=1,2,…,n)个循环周期绿灯相位起始时刻,rij表示在第i个信号交叉口处信号灯第j个循环周期红灯相位起始时刻。
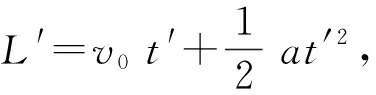
根据城市实际道路环境及安全条件约束,为保证驾驶员或乘客的舒适性,应避免急加速或急减速,故将tp取为红灯-绿灯相位变化的临界点。根据车辆实际到达信号交叉口情景分析,可将车辆不停车通过信号交叉口的驾驶行为分为匀速行驶、加速行驶、减速行驶及停车等待四种。
(1)驾驶行为1:当车辆行驶至交叉路口控制范围内时,获知前方信号灯为绿灯相位,且剩余时间较长,足以在当前绿灯循环周期内以速度v0通过前方信号路口,即L≤v0(tp-t0),a=0;此情形,车辆可保持当前车速v0通过信号路口,车速无须调整。
(2)驾驶行为2:当车辆在交叉口控制范围内,接收到前方信号灯为绿灯相位,但剩余时间不长,若车辆保持初速度v0行驶,在本轮绿灯结束之前无法通过路口,此时车辆需加速一段距离才能确保在本轮绿灯切换之前通过路口,即a>0,设车辆通过信号交叉口时刻为第n个循环周期绿灯结束时刻,即tp=rin,此过程可用以下数学表达式描述:
(1)
(3)驾驶行为3:当车辆行驶前方信号灯为红灯相位,且剩余时间较短,车辆保持当前车速行驶至信号灯路口停车线时,下轮绿灯还未开启,此时车辆须停车等待下轮绿灯开启通行;但如果车辆适当减速,则可在下轮绿灯开启后不停车安全通过路口,即a<0,为确保减速度最小,设通过信号交叉口时刻为tp=gin,且满足以下要求:
(2)
(4)驾驶行为4:当车辆行驶进入通信范围时,获知前方信号灯相位信息为绿灯,且时间I极短或前方信号灯为刚开启的红灯相位,此时,车辆无论怎样加速或减速都无法在当前相位循环结束之前通过该信号路口,则车辆必须停车等待,待下轮绿灯开启后才能通过。
综上所述,通过定性分析如果要实现不停车等待通过信号交叉口,则需执行图3引导决策模型。
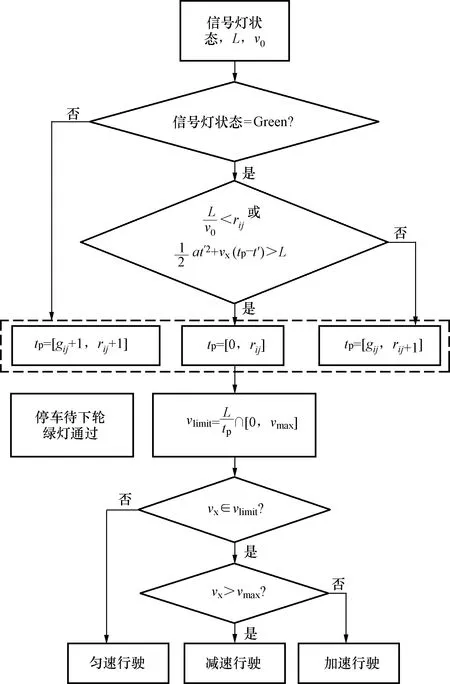
图3 信号交叉口车速引导决策模型Fig.3 Vehicle speed guidance decision model at signalized intersection
2.2.3 目标函数
(1)车辆延误
当车辆m在当前周期内通过信号交叉口时,其通过信号交叉口时刻tp与到达信号交叉口时刻Tiz的差值cm可划分两种情形表示。
①当车辆m在当前绿灯相位时到达信号交叉口,且在本轮绿灯结束之前可以通过该信号交叉口,其差值为0,即符合驾驶行为1、2、3;②当车辆m到路口通信范围时,前方相位信号为红灯或当前绿灯剩余时间不足以车辆安全通过当前路口时,即驾驶行为4,其差值为下一循环k绿灯开始时刻gik与车辆m到达路口停车线时刻Tiz之差。以上两种情形可表达为
cm1=tp-Tiz
(3)
根据车辆实际运行情况cm1≥0恒成立,且目标最小,故当Tiz≤gik时,tp=gik,当gik≤Tiz≤rik时,tp=Tiz。
同理,当车辆m在信号灯下一循环周期通过时,其实通过信号交叉口时刻与到达信号交叉口时刻的差值cm2可表示为
cm2=tp2-Tiz
(4)
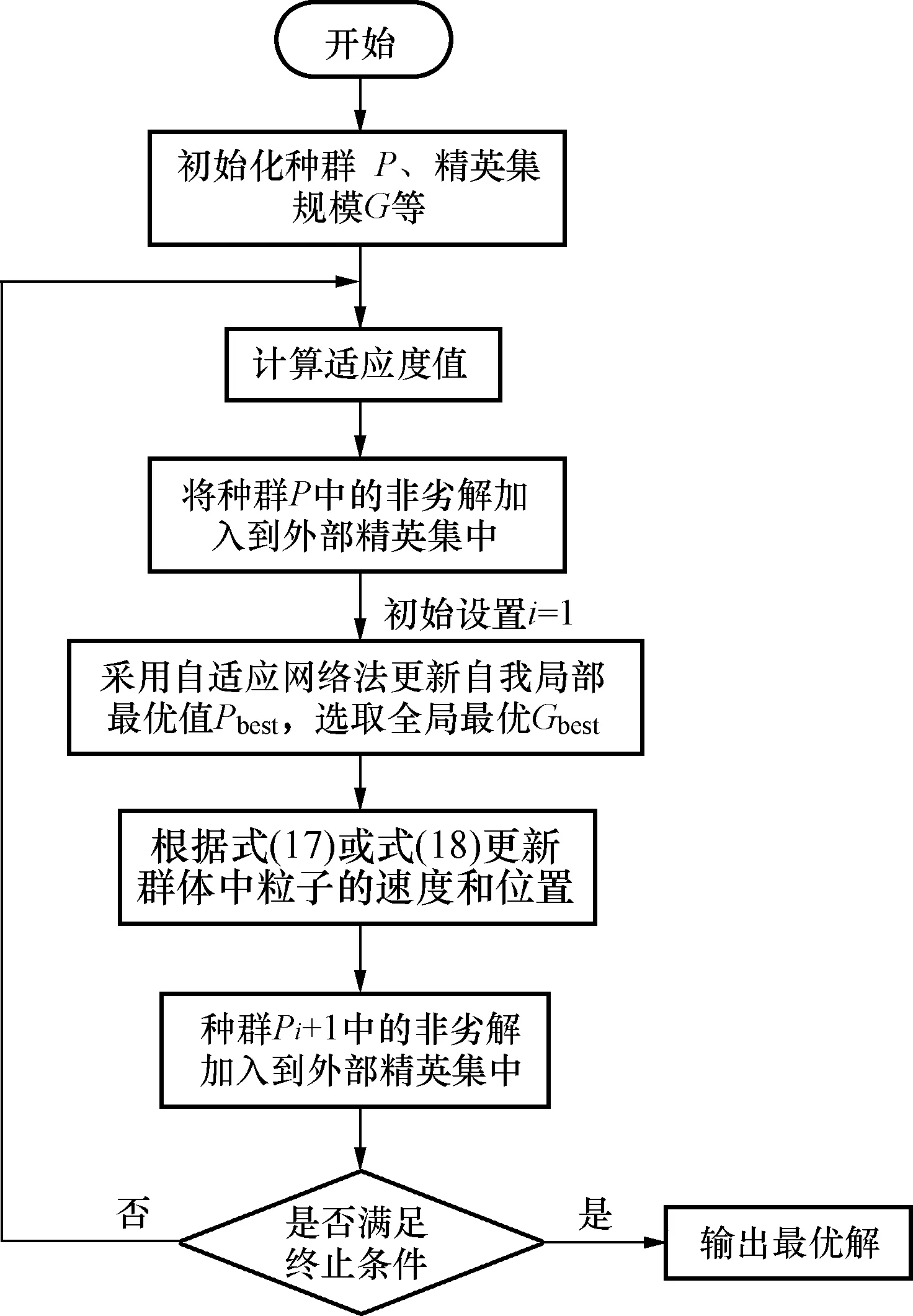
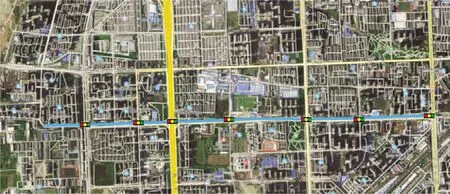
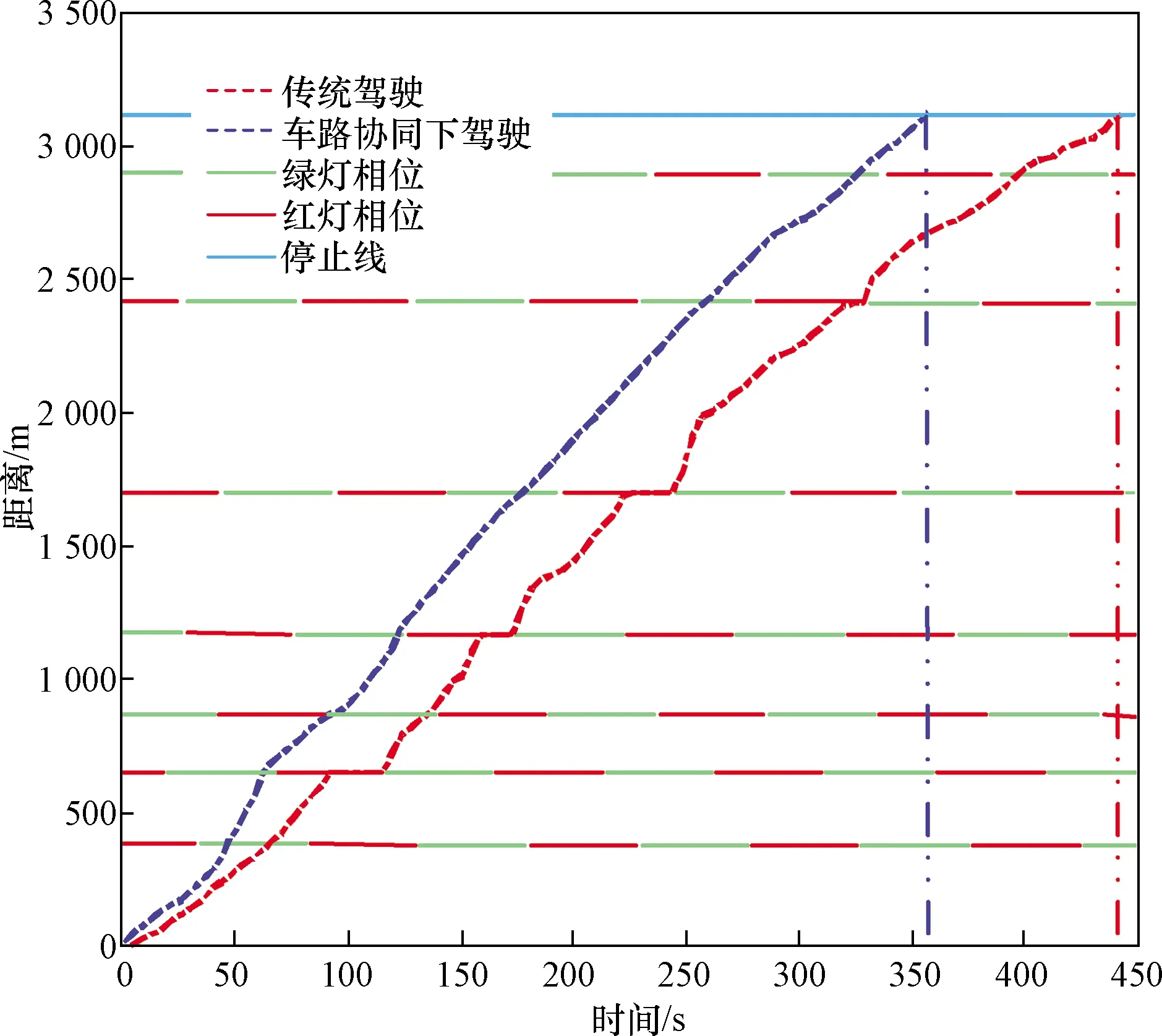
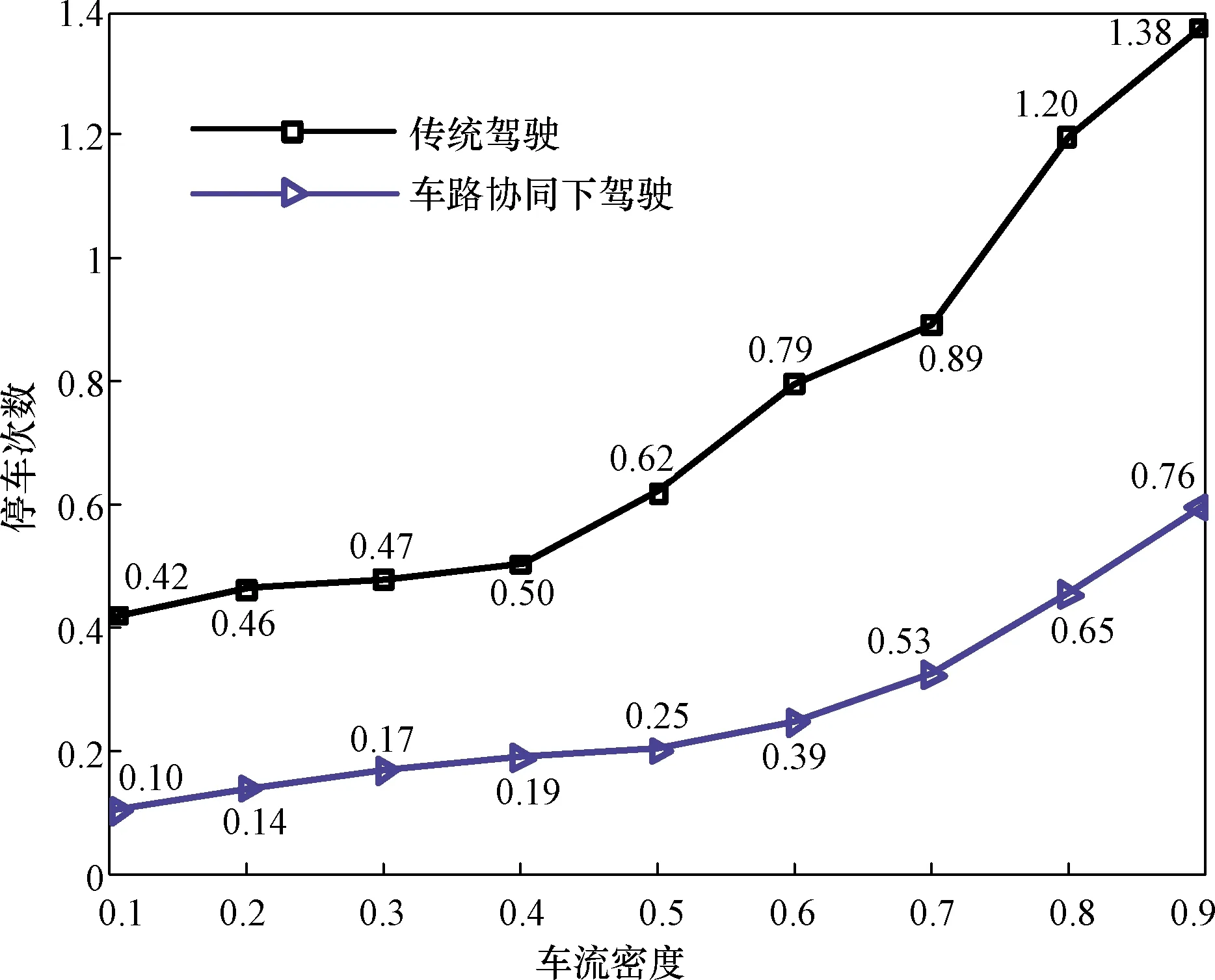
式(4)中:tp2为车辆m在信号灯下一循环绿灯相位通过路口时刻,rik+Ik≤tp2≤gik+Ik,rik 将车辆延误定义为:车辆在车速引导行驶通过信号交叉口时刻与未经车速引导通过信号交叉口时刻的差值,用dij表示。因此,差值cm1、cm2与车辆延误之间的关系为 (5) 式(5)中:dm1表示车辆m在本轮绿灯期间通过信号交叉口时的延误,dm2表示车辆m在本轮红灯结束之后,绿灯开启时通过信号交叉口时的延误。 根据上述驾驶行为分析,当车辆获取前方信号灯相位信息之后,通过当前路口方式可划分为两种:①匀速或通过加/减速不停车在本轮绿灯结束之前通过;②在停止线停车等待,直到下轮绿灯开启通过。基于以上两种通过方式,对于任意车辆i延误可表示为 (6) (2)停车次数 针对车辆停车,用-1或1表示其停车次数,用变量mi表示。当车辆i以驾驶行为1、2或3方式通过路口,其通过信号交叉口时刻tp与到达信号停止线时刻Tiz的差值cm小于ti(车辆i停车前减速时间)时,可避免停车等待,此时,mi=1;反之当mi=-1时,车辆须停车待下轮绿灯相位开启时通过该路口。上述关系可表示为 cm=tp-Tiz (7) Q(mi-1) (8) 式中:Q为一个正实数。 当车辆在道路行驶时,要达到停车次数最少且车辆延误低的目的,其实质是典型的多目标数学问题,求解的目的是使相互冲突的多个目标函数,在可行域内得到最优解集,成为Pareto解集。基于上述分析,多目标数学模型可表述为 F=min(di,mi) (9) 2.2.4 约束条件 城市行车环境复杂,车辆行驶受多种交通参与者影响,为保证行车安全,车辆在信号交叉口控制区域进行车速调整时必须满足以下约束。 (1)通行时刻约束: tp∈(gijrij) (10) 式(10)中:tp为车辆通过信号交叉口时刻;gij为在路口i处第j个周期绿灯开始时刻;rij为在路口i处第j个周期红灯开始时刻。 (2)加速度约束:为保持驾驶员或者乘客在舒适性范围内,应尽量避免急加速或急减速[15]: a=[amin,amax]∈[-2,2] (11) (3)行驶道路限制速度: vlimit∈[vmin,vmax] (12) 式(12)中:vmin设为0;vmax为道路城市道路最高限速。 (4)行车过程中与前车安全间距约束:考虑到驾驶员做出制动动作的延迟及制动减速度,建立的最小安全距离模型为 (13) 同时,考虑前车遇突发情况需紧急制动,此时前后车之间的最小安全距离模型为 (14) 式(14)中:vx为本车车速;an为车辆紧急制动时最大制动减速度。 综上,选取式(13)、式(14)最大的距离d作为最小安全距离,即d=max(d1,d2)。 多目标粒子群优化算法作为一种智能优化算法,每个粒子具有两个特征参数即速度和位置,粒子通过社会认知和自我认知,进行个体速度和位置的更新,逐代搜索寻优,最终获得全局最优解。上述问题是非线性约束下的非线性问题,而用粒子群优化算法(particle swarm optimization,PSO)用于求解有约束优化问题时,必须根据约束条件设置相应的惩罚函数[16]。 根据上述优化问题构造的惩罚函数为 (15) 式(15)中:M是大于零的惩罚因子;pi(x)为惩罚项,当第i个不等式满足约束条件时,pi(x)=1,反之pi(x)=0。 因此,基于多目标粒子群优化算法的经济车速问题的适应度函数为 (16) 速度和位置更新公式如式(17)、式(18)所示: Vi=wVi+C1rand()(Pbesti-Xi)+ C2rand()(Gbest-Xi) (17) Xi+1=Xi+Vi (18) 式中:Vi为粒子i的当前速度;Xi为粒子i的当前位置;w为惯性因子;C1、C2为学习因子;通常C1=C2,Pbesti为粒子i的历史最佳位置;Gbest为种群中的历史最佳位置。 多目标粒子群优化算法与求解单目标的优化算法相比,引入了精英集策略,即选取非劣解“粒子”构成Pareto精英集(或称外部档案,即每一次迭代过程中的非劣解集合)。多目标粒子群优化算法具体流程如图4所示。 图4 多目标粒子群优化算法执行流程图Fig.4 Flow chart of multi-objective particle swarm optimization algorithm 为验证建立的车速引导模型及算法的有效性,利用智能汽车仿真软件PreScan 内部V2X模块及虚拟传感器系统建立智能网联环境感知交互体系、应用MATLAB/Simulink开发实现对行驶车辆的控制策略,最后利用交通仿真软件Vissim快速生成逼近现实情景的交通流场景,结合三种仿真软件特点,搭建了如图5所示的可实现环境感知、 规划决策和控制执行的智能汽车“软件在环”一体化仿真测试平台,对所提车速规划方法进行仿真验证。 图5 一体化仿真测试平台Fig.5 Integrated simulation test platform 图6 模拟的真实路线Fig.6 A real-world route map for the simulation 表1 相邻信号灯之间的距离Table 1 Distance between adjacent signals lights 表2 各信号交叉口信号灯相位信息Table 2 Phase information of signal lights at signalized intersections 为验证提出的车速引导模型在不同交通状态下的表现形式,在Vissim中建立交通流时,分别以不同的交通流密度来表征该路段不同时间段的交通状态,所对应的交通流密度为0.1~0.9。 通过智能汽车一体化仿真平台得到的车辆在交通流密度为0.4时空轨迹如图7所示。从图7可以看出,车速在无引导车速指引下通过第2、4、5、6个信号交叉口时出现不同时长的停车等待,车辆出现急剧的减速;而在车路协同环境下,当车辆获取前方信号灯相位信息后,可通过模型判断是否能以当前车速通过,在车速引导控制下车辆严格遵守2.2.2节分析的驾驶行为规则。从图7可以看出,相较于传统驾驶,在有车速引导条件下车辆行驶轨迹更平缓,减少了车速“突变”现象,在该环境下避免了急减速/加速情况,使其加/减速过程更平缓。 图7 车辆时空轨迹Fig.7 Spatio-temporal trajectories of vehicles 如图7所示,就车辆通过第2个、第3个信号交叉口进行分析。在有车速引导条件下,在车辆通过第2个路口时,车辆判断不能以当前车速在本轮绿灯结束之前匀速通过后,先以0.36 m/s2的加速度行驶11 s,之后维持该速度匀速行驶可在本轮绿灯结束之前通过该路口,避免了在此路口的停车;在通过第3个路口时,车辆先匀速行驶10.79 s,再以1.078 m/s2的加速度行驶3.6 s后,维持该速度匀速行驶,恰好在下轮绿灯开始时刻通过该路口。 由图7可以看出,在无车速引导下,车辆因速度分配不合理而在路口停车等待,导致增加额外的燃油及行程时间,而所提出的车速引导模型,利用车路协同技术获知周围环境信息,规划出合理行车速度,有效避免了车辆红灯停车现象。依据仿真结果,在相同车流量下,以传统驾驶方式通过模拟的 7个路口,行程时间为443.7 s;而在车路协同引导下,行程时间为360.4 s,可节约18.7%的行程时间。 4.2.1 停车次数分析 定义车速低于3 km/h时,即视为车辆处于停车状态。根据仿真实验记录下的车辆位置、速度等信息,可计算出每辆车在不同车流密度下速度引导前后的停车次数,进而得到平均每辆车的停车次数,如图8所示。 图8 车速引导前后停车次数对比Fig.8 Comparison of the number of stops before and after the speed of the vehile 由图8可以看出,车流密度在0.4以下时,停车现象均减少62%以上;在最高车流密度下,其优化比例也达到44%以上。在车路协同引导驾驶下,无论在低、中、高何种车流密度下,平均停车时间均明显减少。在中、高密度车流量中,车辆停车次数优化结果相对于低密度车流量效果差,其由于在高密度车流中,传统驾驶的车辆速度不受控制,如果前方遇到红灯,车辆则减速停车而造成后续车辆不得不停车,从而增加了后续车辆的停车次数;而在速度控制之下可以使整条运行线路的车速趋于平稳,从而使整个交通流的运行更加通畅。因此,在交通流量较大时更能体现车路协同环境下车速引导的重要性。 4.2.2 停车延误分析 图9结果表明,在车路协同引导驾驶下,车辆延误出现不同程度的降低,特别是在低车流密度下效果显著,优化比例在65%以上。随着车流密度的增加,优化效果有所下降,在高车流密度环境下其优化效果仅保持在16%左右,此情形是由于在高密度车流下,一个绿灯循环不足以使后续车辆全部通过,有的车辆需经过2次绿灯循环才能通过,从而增加了交叉口的延误,导致优化效果不佳。仿真结果表明,提出的车速控制引导模型及车速求解算法适用于不同的交通状况。 图9 车速引导前后延误对比Fig.9 Comparison of delay before and after vehicle speed guidance (1)提出了基于信号灯状态的车辆经济车速规划方法。利用PreScan+Vissim+MATLAB/Simulink仿真测试软件搭建了可实现环境感知、规划决策和控制执行的智能汽车“软件在环”一体化仿真测试平台,完成了车路协同环境的构建。车辆在车路协同环境下可获取车辆行驶前方的信号灯相位信息,在保证安全、舒适的前提下,对车辆不停车通过信号交叉口的经济车速进行规划,使车辆得以快速平滑地通过信号交叉口。 (2)通过PreScan、Vissim与MATLAB/Simulink联合仿真,结果表明采用车速规划方法后,车辆可实现避免红灯停车通过前方信号交叉口。 (3)通过提出的车速引导方法,可节约18.7%的行程时间;在高车流密度下,可至少减少44%的停车次数;车辆延误在低密度车流下效果明显,可降低65%以上。
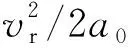
3 基于多目标粒子群算法的经济车速求解
4 仿真及验证
4.1 仿真平台

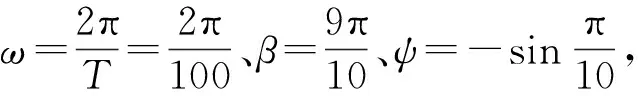


4.2 仿真结果分析

5 结论

