考虑土体小应变刚度的地表堆载对隧道影响数值分析

卞 荣, 刘华清, 陈 飞, 吴 冰, 贺 雷, 叶冠林

(1. 国网浙江省电力公司经济技术研究院，杭州 310012；2. 中国电力科学研究院有限公司，北京 100192；3. 上海交通大学船舶海洋与建筑工程学院，上海 200240)

近年来，随着城市基础设施建设以及地下空间的快速发展，地下建筑物、构筑物变得逐渐密集，隧道的变形问题也越来越受到人们的重视[1-3]。地面堆载是引起既有隧道变形的重要因素，会对隧道产生非常不利影响。然而实际工程中对于隧道的变形要求是非常严格的，以地铁隧道为例，隧道的绝对最大位移需小于20 mm，隧道曲率半径应大于15 000 m，而相对弯曲要小于1/2 500[4-5]，一旦隧道变形过大，隧道就极易发生环缝开张过大而导致漏水或者管片破坏等问题。上海打浦路的越江隧道就由于地表堆载的问题而出现了严重的不均匀沉降问题，堆载引起的总沉降高达110 mm[6]。因此，研究地面堆载对既有隧道结构的影响与控制是十分重要的。

针对上部堆载对既有隧道影响的问题，学者分别采用理论、试验和数值等手段进行了探讨与研究。早期学者们常采用理论解析方法研究既有隧道的变形问题。陆文超[7]通过复变函数解法分析地面堆载引起隧道围岩的平面弹性应力问题；房营光等[8]采用对称性原理方法得到了隧道围岩应力与变形的解析解；柯宅邦等[9]在新提出的地基模型中引入了土体变形非线性的概念，推导求得地表堆载影响下既有隧道纵向变形的简化解；康成等[10]基于将既有隧道简化为Timoshenko 梁的考虑，提出了既有隧道在地表堆载下受力和变形的简化解析解。但一般而言建立的计算模型与隧道实际的变形情况有较大出入，进行了较多的简化处理。模型试验是研究堆载引起隧道变形的最直观手段[11]。吴庆等[12]通过室内模型试验方法研究了盾构隧道周围堆载对其变形的影响；汪洋等[13]通过建立室内模型试验，对盾构隧道施工引起的既有隧道纵向附加弯矩和轴力以及变形进行了模拟计算。然而通常情况下由于模型试验造价较高且难度较大而较少采用。近年来，随着计算机技术的发展，采用数值方法研究堆载对既有隧道影响的问题得到了快速发展。戴宏伟等[6]采用数值方法探讨了上部堆载的位置、隧道的埋深和直径以及土层特性的影响；唐金会等[14]通过建立三维数值模型，对地面堆载对隧道衬砌管片的影响进行了分析；张立明[15]基于有限元分析的方法，对地表堆载位于隧道的正上方和侧上方两种情况对隧道的变形影响进行了计算分析。冷建等[16]通过建立数值分析模型，对隧道埋深、堆载高度、堆载宽度对隧道上浮量的影响进行了分析。

在采用数值方法分析堆载对隧道的影响问题时，选用合理的土体本构模型非常重要。摩尔-库伦模型(M-C模型)在岩土工程领域广泛应用，而考虑土体小应变特性的硬化本构模型(HSS模型)在中国江浙沪一带的软土地区得到了越来越多的应用[17-18]。为探究两个模型对实际工况的模拟情况，将分别采用M-C模型和考虑土的小应变特性的HSS模型对地表堆载条件下既有隧道的变形问题进行研究，分析比较二者区别，为相关保护规范的建立提供支持。

1 有限元模型及材料参数

基于宁波澄浪隧道地勘报告的相关内容，以该隧道为例，研究既有隧道在其他参数不变时，顶管的埋深和堆载位置对隧道变形的影响。数值模型的计算简图和网格划分情况如图1所示，数值模型在隧道附近进行局部加密处理，最小尺寸为0.6 m，总网格数为 1 924。顶管隧道模型采用宁波澄浪隧道的尺寸，其外径为3.54 m，内径为3.0 m。模型顶面为自由边界，其余边界受法向约束。

图1 数值模型计算简图及网格划分Fig.1 Sketch computational mesh of the numerical model

1.1 M-C本构模型相关参数

参照宁波澄浪隧道地勘报告，建立分层土模型，采用大变形模式，土层材料采用M-C本构模型，相关参数如表1所示。隧道管节材料采用线弹性横观各向同性模型，参数如表2所示，并做如下假设：①假设地表面和各土层均呈水平层状分布；②考虑土体自重应力场；③不考虑地下水渗流对顶管的影响。

表1 土体物理力学参数Table 1 Physical-mechanical parameters of soil

表2 顶管管节衬砌材料参数Table 2 Lining material parameters of pipe jacking joint

1.2 HSS本构模型相关参数

分层土模型采用软黏土地区典型的上下层硬，中间层较软的“硬-软-硬”构造，分别对应上海软土的第2、4、6层土，与宁波澄浪隧道所处地层条件是接近的，以此建立分层土模型。土层材料参数采用可以考虑土体小应变特性的HSS模型，相关参数如表3所示。顶管隧道管节材料采用线弹性横观各向同性模型，具体参数如表4所示。

表3 HSS模型下土体物理力学参数Table 3 Physical-mechanical parameters of soil in HSS constitutive model

表4 HSS模型本构参数Table 4 Parameters of HSS constitutive model

2 堆载大小对扰动影响

首先建立一个宽度为15 m，堆载分别为20、40、60、80、100 kPa，从而研究堆载大小对土体影响范围的影响规律，计算结果如图2所示。

由图2可知，随着堆载的增大，堆载对土体影响范围越来越大，但影响范围的增幅逐渐减小，HSS本构下得到的土体受堆载影响范围远低于M-C本构的计算结果，M-C本构的侧边和深度影响范围达到了75 m的尺度，但HSS本构下侧边及深度影响范围仅为35、30 m左右。堆载大小为20、100 kPa位移云图如图3、图4所示，其中左侧为M-C模型计算结果，右侧为HSS计算结果。

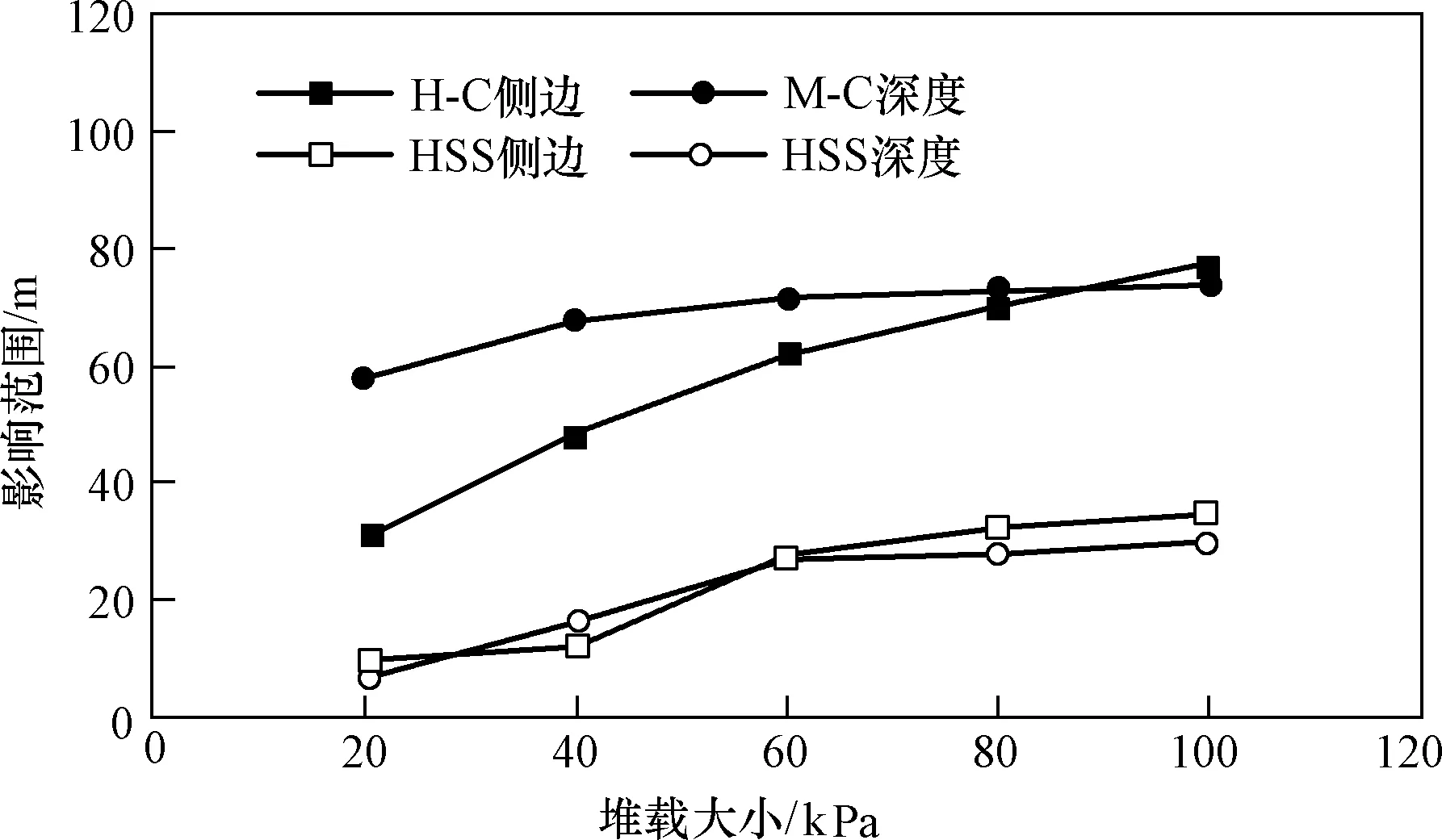
图2 M-C与HSS本构下不同堆载大小的土体影响范围Fig.2 Influence range of soil under various heaped loading with M-C and HSS consitutive model

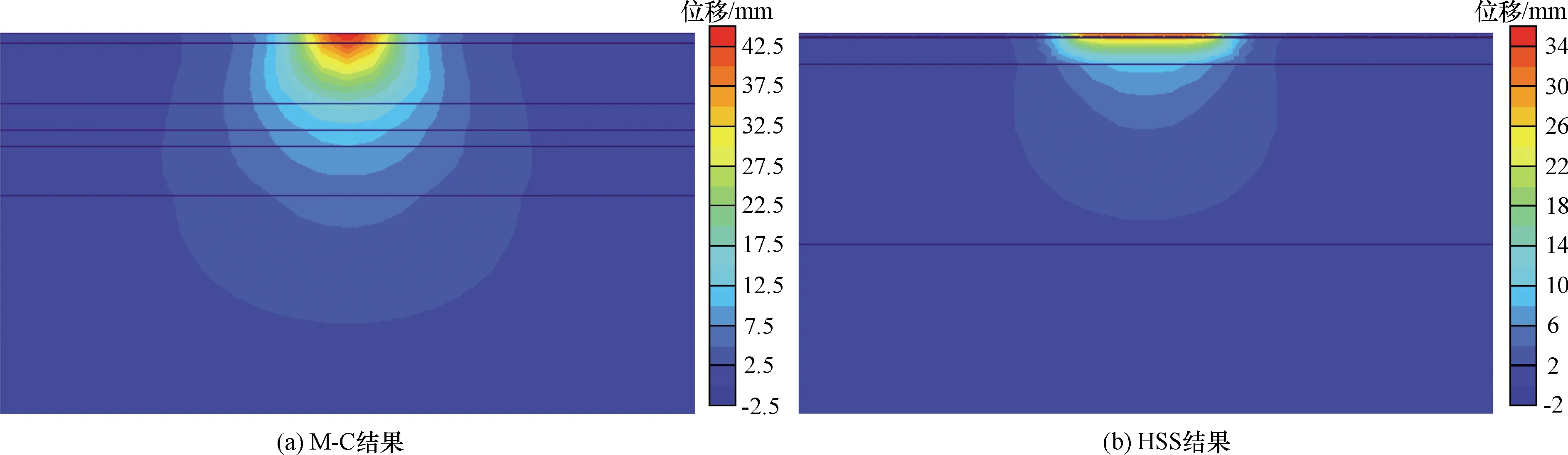
图3 堆载为20 kPa的位移云图Fig.3 Nephogram of displacement when heaped load equals to 20 kPa

图4 堆载为100 kPa的位移云图Fig.4 Nephogram of displacement when heaped load equals to 100 kPa

3 堆载尺寸对扰动影响

堆载尺寸同样会对土体产生明显影响，在此以堆载大小80 kPa为例，研究堆载宽度分别为5、10、15、20、25 m情况下堆载尺寸的影响范围，具体结果如图5所示。

从图5可以发现，堆载宽度越大，其侧边及深度方向的响范围也越来越大，但增幅呈现减小的趋势。但从数值上，HSS本构下得到的土体受堆载影响范围仍远低于M-C本构的计算结果，M-C本构的侧边和深度影响范围达到了75 m的尺度，但HSS本构下影响范围深度不超过35 m，侧边则不超过40 m。与图2结果对比可以发现，在该工况下由 M-C本构计算的结果偏离实际较多，而HSS本构更加贴合工程实际。

图5 M-C与HSS本构下不同堆载堆载宽度的土体影响范围Fig.5 Influence range of soil under various heaped loading width with M-C and HSS consitutive model

4 隧道埋深对扰动影响

现以堆载宽度25 m，大小为80 kPa的典型组合作为代表，以宁波澄浪隧道内径D=3 m的尺寸，计算顶管隧道在不同埋深下，地表堆载对隧道的影响，计算结果整理成如图6所示。

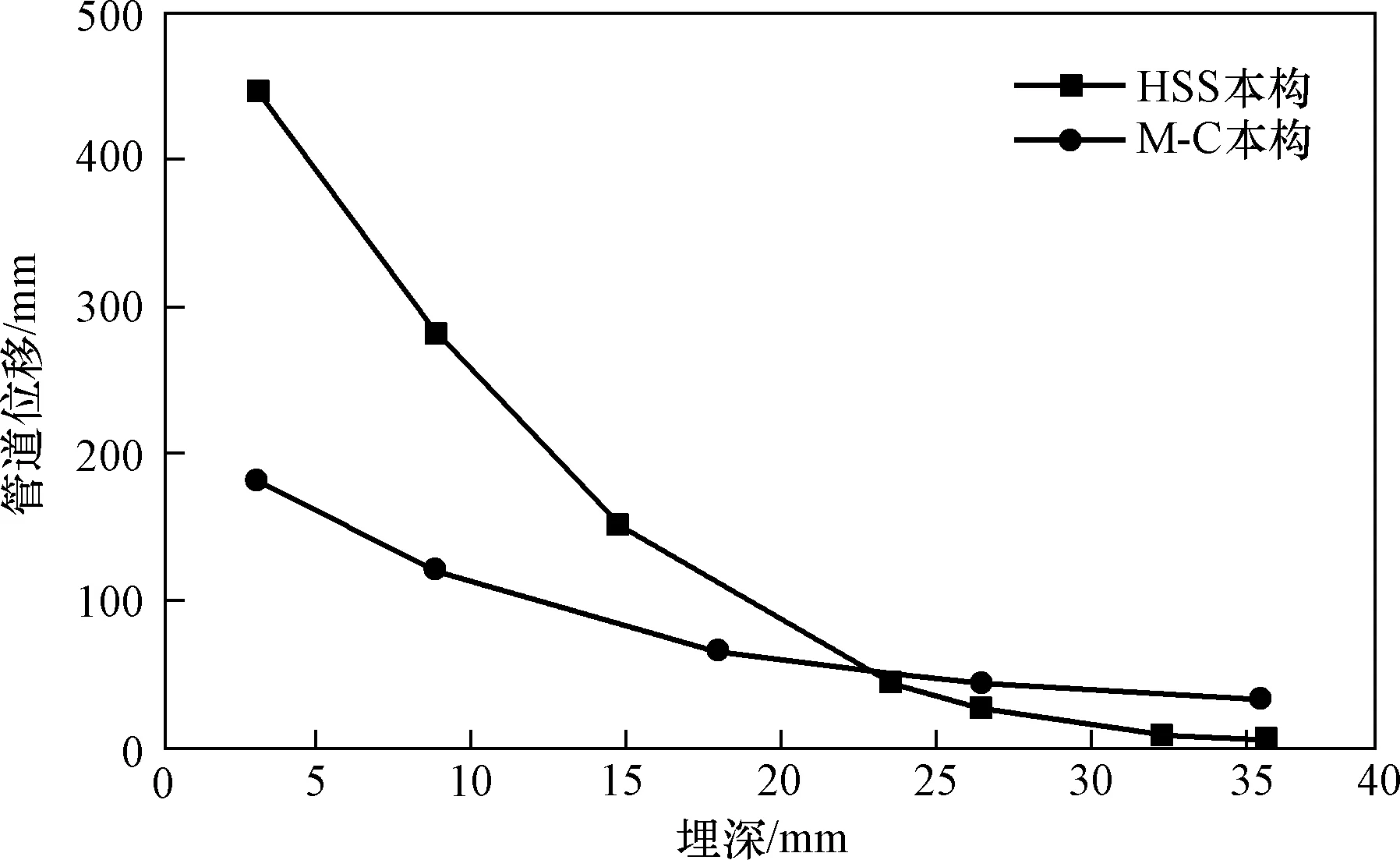
图6 地表堆载正下不同埋深管道最大位移Fig.6 The maximum pipe displacement under heaped loading with various pipe buried depth

从图6可以看出，顶管隧道存在正上方堆载时，HSS本构下的管道位移在埋深较浅范围内明显大于M-C本构下的计算值，但其值随着埋深的增大出现较快衰减，在大于埋深24 m后的管道位移要小于M-C本构下的计算值。地面堆载将使其产生较大变形，隧道变形在埋深约28 m范围内会超过位移限制值15 mm，考虑到实际顶管隧道埋深基本不会超过12 m，为了排除堆载太大导致安全埋深过大这一因素的影响，补充计算不同堆载位于顶管隧道正上方时不同埋深的顶管位移，当隧道位移量小于变形安全限值时，即得到安全深度。结果整理如图7所示。

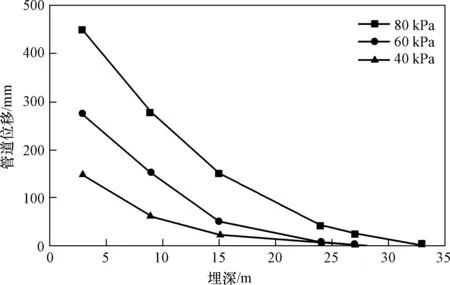
图7 不同荷载大小条件下埋深对管道位移影响Fig.7 The effects of buried depth on displacement of pipe under various heaped loading

计算结果显示，在隧道正上方堆载为80、60、40 kPa 的情况下，隧道的最小安全埋深为18 m，同样远大于实际顶管隧道的埋深，因此应该严禁在下方敷设有顶管隧道的条件下进行正上方堆载，否则极易引起顶管隧道的止水失效破坏。

5 地表堆载安全保护距离

研究表明，采用M-C和HSS本构模型研究隧道上部堆载对土体影响明显，因此合理预测堆载对土体影响范围是十分必要的。隧道上部堆载的影响度划分示意图如图8所示。

红色区域为采取措施区域；黄色区域为需要注意区域；黄色区域外为微影响区域图8 顶管上部堆载影响范围示意图Fig.8 Sketch of affected area for heaped loading upon pipe

以隧道埋深20 m，堆载大小80 kPa，堆载范围25 m条件为例，M-C和HSS本构下不同侧方距离情况下顶管最大位移如图9所示。从图9可以看出，HSS本构结果中，采取措施区域为5 m，需注意区域为25 m；超过25 m为微影响区域；而M-C本构结果中采取措施区域为25 m，需注意区域为80 m；超过 80 m 为微影响区域。M-C本构计算结果中的安全保护距离过于保守，几乎不具有实际可操作性，HSS本构模型计算结果更加贴近工程实际，且是偏于安全的。

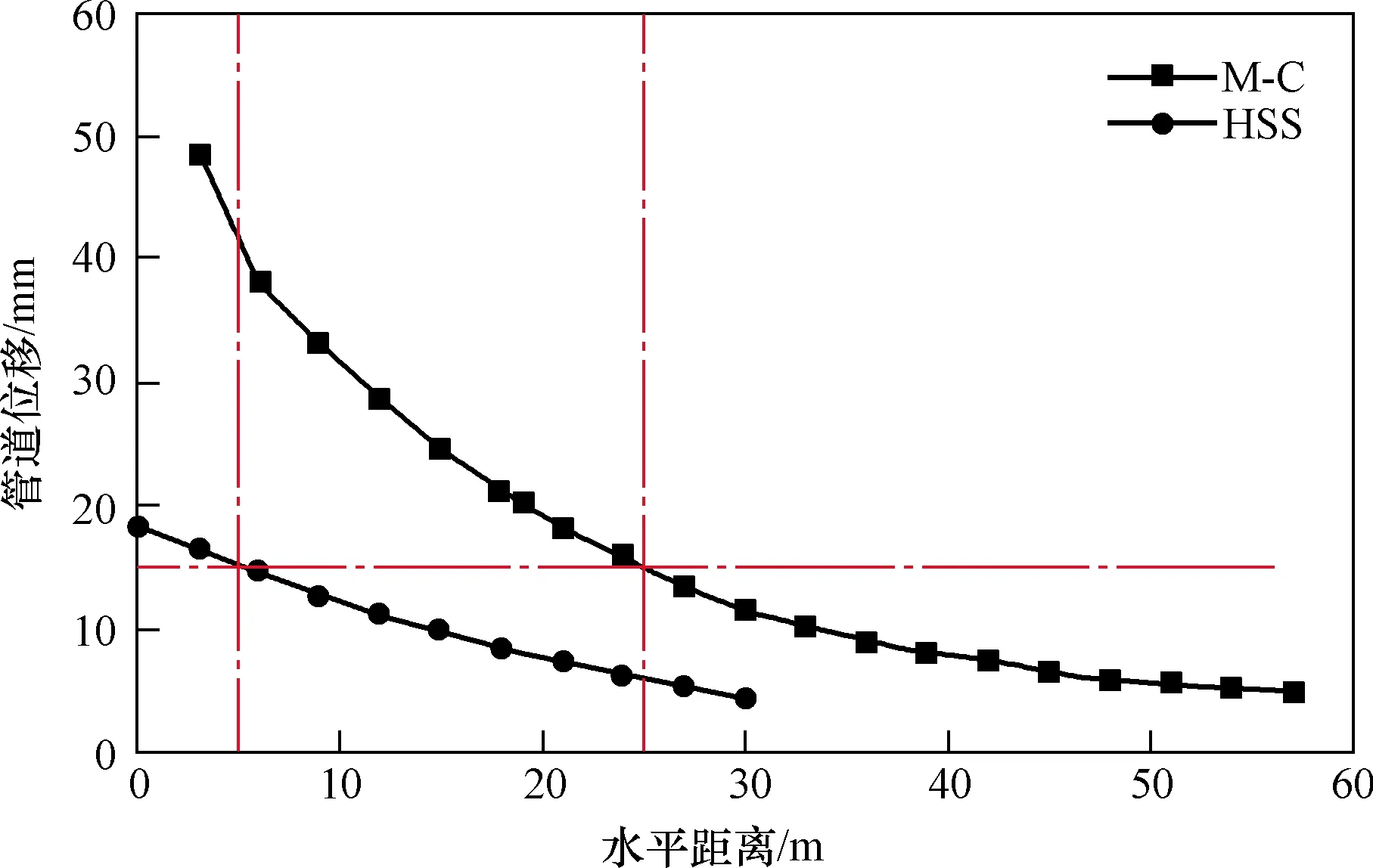
图9 不同水平距离处管道位移Fig.9 The maximum pipe displacement for various horizontal distance

6 结论

对于地表堆载工况对既有隧道扰动变形的影响，堆载的尺寸、堆载大小以及隧道埋深均会影响扰动量：堆载宽度和大小越大，扰动越大；相反隧道埋深越大，扰动越小。此外，HSS本构模型的计算结果要远小于M-C模型的计算结果，且更贴近于工程实际。根据计算结果，建议在隧道正上方堆载对既有隧道的扰动很大，安全深度需超过18 m，超过目前绝大多数顶管工程隧道的埋深，此深度下的隧道的维修和维护等工作开展会有较大困难，因此建议禁止在既有隧道的正上方进行堆载。