砂土地基强夯室内模型试验及加固特性分析

王 锃, 郑凌逶, 罗嗣海, 谢新宇, FRIEDEMANN Sandig

(1. 江西理工大学建筑与测绘工程学院，赣州 341000；2. 浙江大学宁波理工学院，宁波 315100；3. 德国莱比锡应用技术大学，莱比锡 04277)

强夯法[1]利用夯锤从较高处下落对地基土形成冲击，使地基土在短时间内产生较高应力，土体孔隙减小、土体密实度提高[2]；自20世纪70年代首次应用于工程实践后，在砂土、粉土、软黏土、碎石土等不同类型地基加固工程中得到广泛研究与应用[3-6]。

与强夯法相关的研究主要集中在：夯锤-地面接触应力、强夯有效加固范围、夯后地基承载力与沉降、夯后土体特性变化等。刘汉龙等[7]根据动力分析中应力边界与速度边界的关系，将应力边界时程转化为速度边界时程，并引入正弦荷载函数，进行了强夯作用下土体竖向位移的简化计算。Zou等[8]结合室内试验与现场试验，对红砂岩土石混合料路堤进行了4种能级的强夯，得到了不同深度的动应力、竖向位移、水平位移等值线，有效加固深度约4.0～6.0 m、加固范围约3.0～4.0 m。Feng等[9]采用12 000 kN·m的高能级对湿陷性黄土进行了现场强夯地基处理，处理后的地基承载力允许值与加固深度分别高于250 kPa和10 m，黄土的湿陷性大大降低或消除。Ghanbari等[10]采用强度折减法对不同坡度的边坡进行了强夯冲击数值模拟，相对于平地，在边坡附近的压密区更窄、夯坑深度随着边坡坡度的增大而加深。

在强夯机理研究中，贾敏才等[3]通过在可视室内强夯模型试验箱分层铺设染色红砂，观测每次夯击后的土体竖向位移，绘制出砂土颗粒竖向位移场等值线图，获取击数与竖向影响深度和水平影响宽度的关系。冯世进等[11]设计了半模试验箱搭配测试动应力的微型土压力盒，进行了强夯法加固粉土地基的室内模型试验，分析强夯作用下动应力和位移等值线变化规律，获取影响深度与夯坑深度比值。

粒子图像测速法(particle image velocimetry,PIV)最初是应用于流体力学的一种光学测量方法，通过追踪标记粒子的运动来测量瞬时流速[12]。随着PIV技术引入岩土模型土壤变形测量以来，在数字图像相关方法(digital image correlation,DIC)取得了不少改进，包括图像强度插值和变形参数优化等[13-14]，能够较好地测量土体位移场发展变化[15]。

砂土地基密实度对于强夯法加固有着重要影响。为此，采用自行设计的模型试验装置及量测系统，制备3种相对密实度的砂土进行强夯室内模型试验；强夯过程中测量夯锤速度、位移、动态力、能量释放时间变化；结合PIV技术分析强夯后砂土颗粒位移结果，得到水平方向和深度方向的有效加固范围发展特性，分析德国莱比锡砂土地基强夯加固特性。

1 模型试验设计

1.1 模型试验装置及量测系统

模型试验装置由一个双层的金属框架以及水平导轨、竖直导轨组成，安装在试验箱上部，试验箱尺寸为70 cm(长)×19 cm(宽)×90 cm(高)。试验箱上部为透明有机玻璃板，可通过高速摄像机记录强夯处理过程中砂土颗粒的运动影像。夯锤质量为4.5 kg，夯锤底面形状为矩形，底面尺寸为18 cm(长)×15 cm(宽)；夯锤顶部安装速度传感器，测量夯锤在强夯试验过程中的动态速度变化；强夯试验过程中，将水平导轨、竖直导轨固定在合适的位置以确保夯锤沿着竖直导轨运动并紧贴试验箱内壁下落。

模型试验装置及量测系统如图1所示。

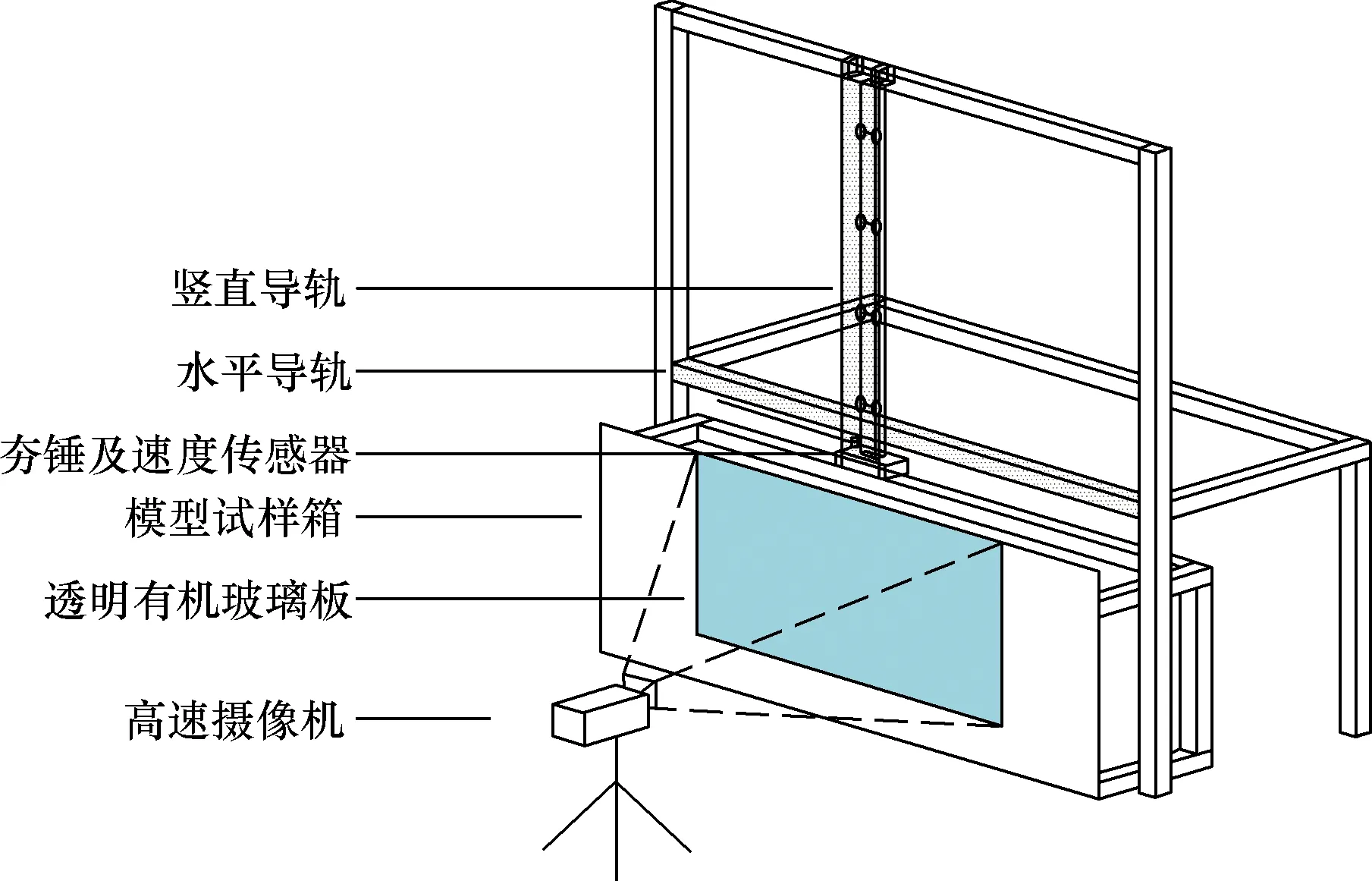
图1 模型试验装置及量测系统Fig.1 Model test device and measuring system

1.2 试验材料

试验采用的砂土取自德国莱比锡市赫希菲尔德地区，物理力学性质如表1所示，粒径分布曲线如图2所示。

表1 砂土的物理力学性质Table 1 Physical and mechanical properties of the sand

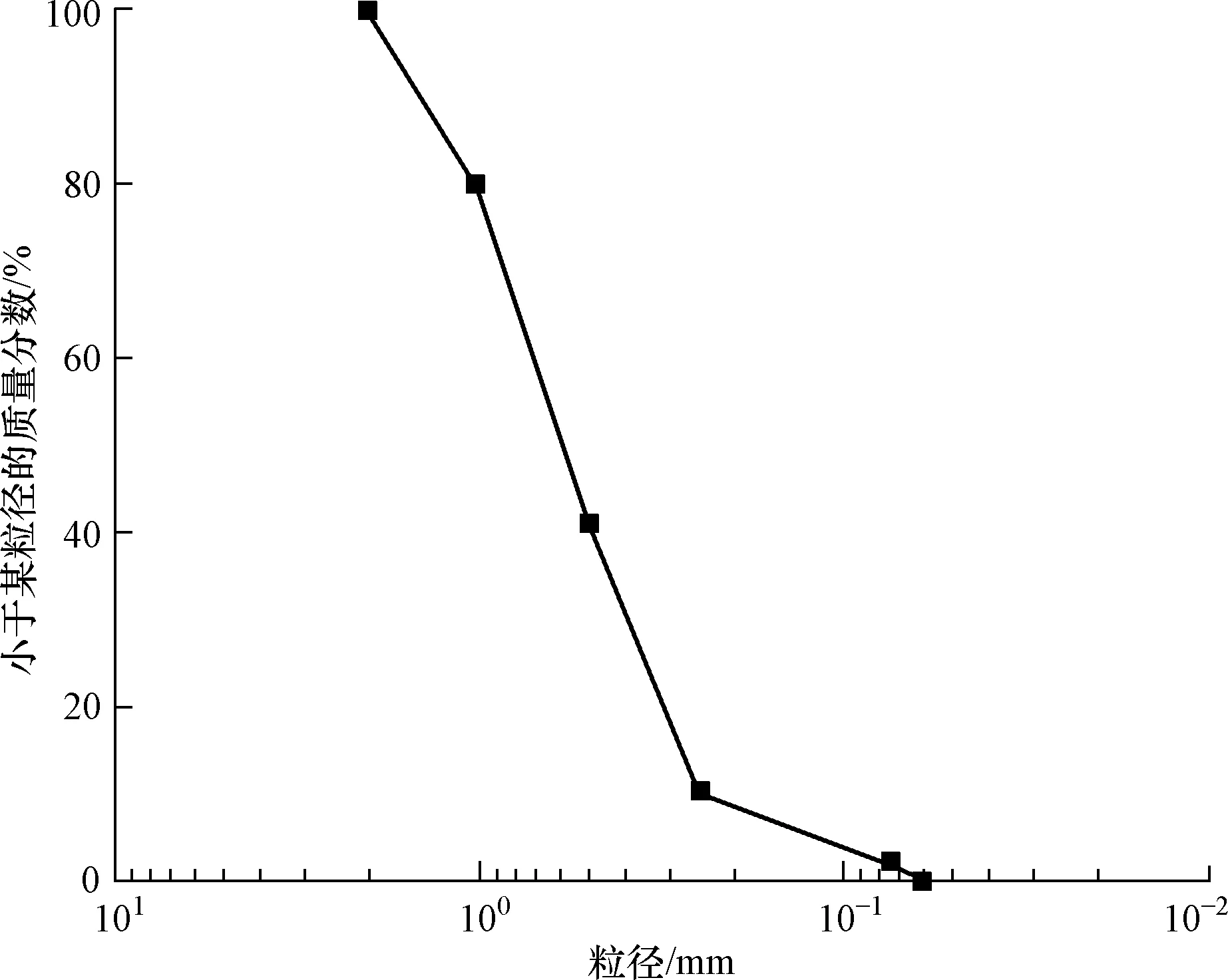
图2 砂土粒径分布曲线Fig.2 Size distribution curve of the sand

1.3 试验方案

砂土的相对密实度ID通常用于描述压实程度，定义为

(1)

式(1)中：ID为砂土的相对密实度，无量纲；ρd-max为砂土最大干密度，g/cm3；ρd-min为砂土最小干密度，g/cm3；ρd为砂土干密度，g/cm3。

通过预试验获取莱比锡砂土相对密实度与落砂高度的关系，如图3所示。

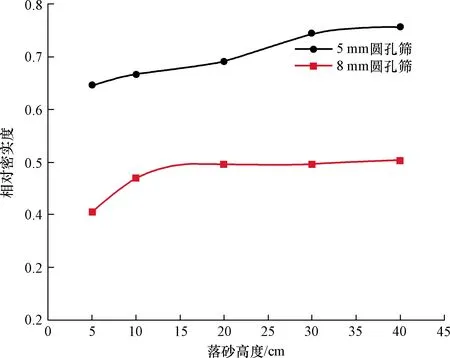
图3 砂土相对密实度与落砂高度的关系Fig.3 Relationship between relative density and fall height of the sand

由图3可知，采用8 mm方孔筛以及5、25 cm落砂高度可以制得相对密实度(ID)为0.4、0.5的砂土；采用5 mm圆孔筛以及22 cm落砂高度可以制得ID为0.7砂土。采取不同的落砂高度、筛网，使用落雨法分层填筑到模型试验箱内，最终形成ID0.4、ID0.5、ID0.7这3组不同相对密实度的砂土地基，填筑高度统一为80 cm。落雨法的具体步骤为：①控制漏斗底部与砂样表面的距离为采取的相应落砂高度，在试验箱正上方位置开始落砂；②落砂过程缓慢往复式移动漏斗，并根据下方砂土积累的厚度逐步调整落砂高度；③到达填筑高度后，采用小平铲对砂土地基表面进行细微修整。

每组试验进行24击强夯，夯锤每次下落高度为100 cm。强夯过程中，采用安装在夯锤上的速度传感器记录夯锤速度时程曲线，并进一步微分处理获得夯锤加速度/动态力时程曲线；采用高速摄像机记录夯锤位移时程曲线，并结合夯锤动态力时程曲线绘制夯锤动态力-位移曲线。强夯加固后，结合PIV技术分析砂土颗粒位移情况，分析砂土地基在水平方向和深度方向的有效加固范围发展特性。

2 试验结果及分析

2.1 夯锤速度时程曲线

为了分析不同相对密实度砂土(ID0.4、ID0.5、ID0.7)与夯击次数对夯锤速度的影响，绘制第6、12、18、24击强夯过程中的夯锤速度时程曲线，如图4 所示。

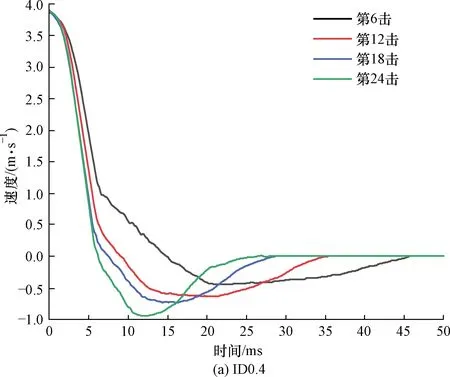
图4 夯锤速度时程曲线Fig.4 Velocity-time curves of the tamp

夯锤速度时程曲线(图4)表明，由于受到导轨摩擦影响，夯锤接触砂土地基表面时的实际夯击速度为3.9 m/s左右，略低于理论计算夯击速度 4.4 m/s。夯锤在与砂土地基表面接触前5 s速度快速下降，第6、12、18、24击的速度时程曲线在快速下降阶段基本重合；随后夯锤进入速度缓慢下降阶段并逐一回弹，击数越高回弹速度越高、持续时间越短，体现为能量释放时间的不同。对于不同相对密实度砂土(ID0.4、ID0.5、ID0.7)，相对密实度越高，夯锤速度下降越快、回弹速度越高，能量释放时间也相应缩短。由于ID0.7试验组砂土的相对密实度在夯前已经较高，颗粒间空隙能够压缩的余地更小，不同击数之间的差别相对也小。

2.2 能量释放时间

根据夯锤速度时程曲线，按夯锤接触土体至夯锤停止运动时刻计算能量释放时间，如图5所示。

图5 能量释放时间与夯击次数的关系Fig.5 Relationship between energy release duration and tamping times

由图5可知，随着夯击次数的增加，夯锤的能量释放时间逐渐缩短；对于不同相对密实度的ID0.4、ID0.5、ID0.7试验组，总体上相对密实度越高，夯锤能量释放时间越短。对于ID0.4、ID0.5、ID0.7试验组，从第6击到第24击的强夯能量释放时间分别下降38.9%、34.7%、31.4%。强夯作用下砂土颗粒由相对松散排列转变为咬合更为紧密的排列，颗粒间空隙减少，宏观上表现为砂土地基承载力提升，夯锤能量释放时间随着夯击次数增加而逐渐缩短。

2.3 夯锤位移时程曲线

为了分析不同相对密实度砂土(ID0.4、ID0.5、ID0.7)与夯击次数对夯锤位移的影响，绘制第6、12、18、24击强夯过程中的夯锤位移时程曲线，如图6 所示。

图6 夯锤位移时程曲线Fig.6 Displacement-time curves of the tamp

夯锤位移时程曲线(图6)表明，随着夯击次数的增加，砂土地基承载力、变形模量不断增大，表现为单次夯沉量逐渐减小、回弹比(回弹量/最大夯沉量)逐渐提高；ID0.4、ID0.5、ID0.7试验组在第24击的夯锤位移回弹比分别达到65.3%、67.1%、69.0%。

2.4 夯锤加速度/动态力时程曲线

为了分析不同相对密实度砂土(ID0.4、ID0.5、ID0.7)与夯击次数对夯锤加速度/动态力的影响，将第6、12、18、24击强夯过程中的夯锤速度时程曲线微分处理获得夯锤加速度时程曲线，根据夯锤质量计算得到夯锤动态力时程曲线，如图7所示。

图7 夯锤加速度/动态力时程曲线Fig.7 Acceleration/force-time curves of the tamp

从图7可以看出，夯锤加速度/动态力时程曲线首先迅速达到一个较高的峰值，夯击能量大部分在此阶段释放；随后加速度/动态力快速下降并在较短时间内保持为一个平台区，然后缓慢降至零。随着夯击次数的增加，加速度峰值逐渐增大、冲击力释放时间缩短；相对密实度越高，夯锤冲击力越大，第6、12、18、24击之间的差别越小。砂土相对密实度越高，颗粒之间咬合越紧密、空隙越少，能够在更少的夯击次数下得到有效加固。

2.5 动态力-位移曲线

得到夯锤位移时程曲线与动态力时程曲线后，可进一步绘制夯锤动态力-位移曲线，以ID0.4试验组为例，如图8所示。

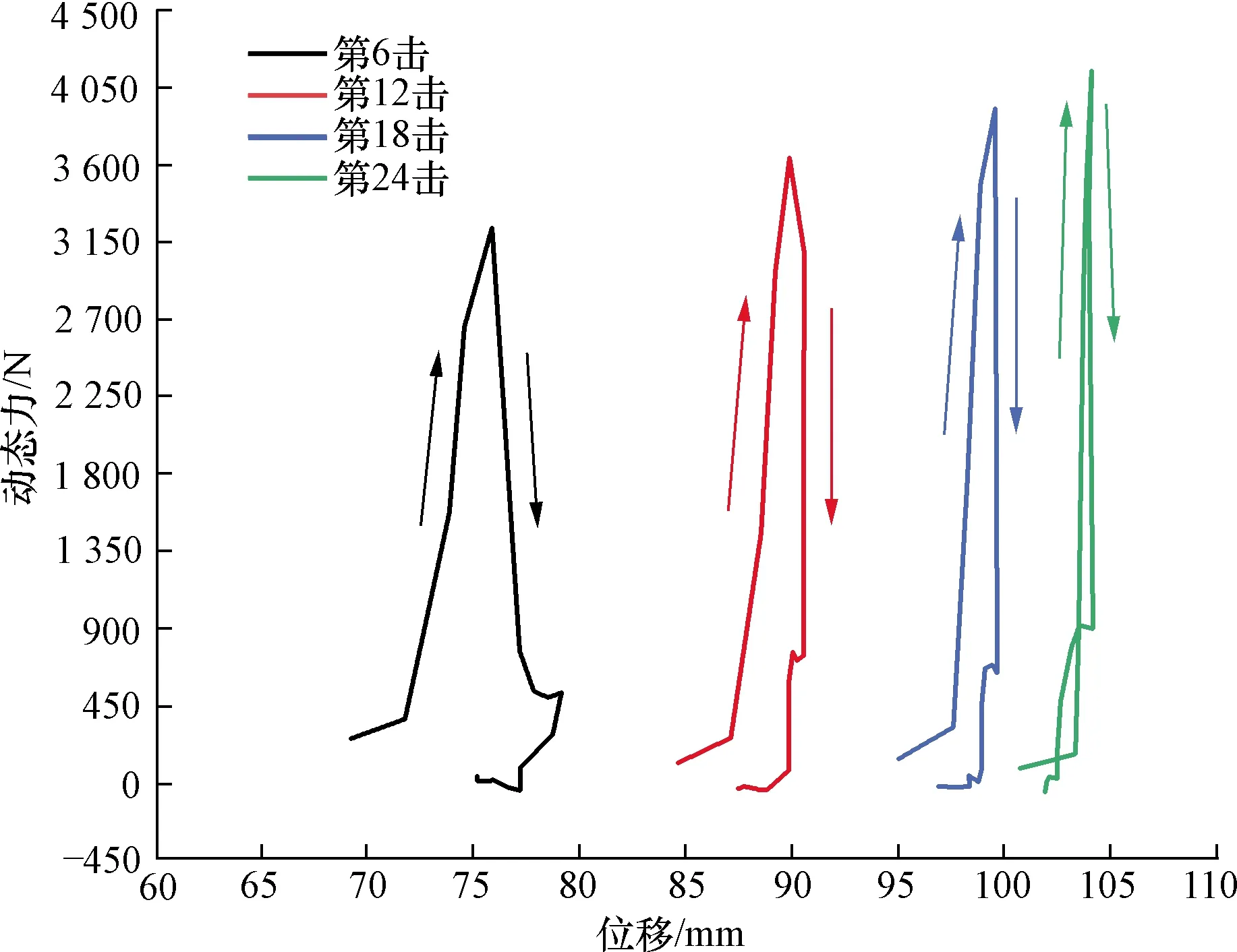
图8 夯锤动态力-位移曲线(ID0.4)Fig.8 Dynamic force-displacement curves of the tamp(ID0.4)

夯锤动态力-位移曲线(图8)结果表明，随着夯击次数的增加，夯锤动态力峰值逐渐提高、上行曲线斜率变小，冲击行程逐渐缩短。在此过程中，砂土地基受到瞬时冲击荷载及剪切力的反复作用，改变砂土颗粒原有的接触形式而产生位移，形成更为稳定的接触形式，土体强度和刚度逐步提高，并表现为夯锤动态力-位移曲线的改变。

2.6 有效加固范围分析

强夯试验前，先利用PIV坐标黑白校准板以及有机玻璃板上的PIV坐标轴校准辅助点进行校准。由于砂土颗粒自带跟随性和散光性，可以起到示踪粒子的作用，所以不需要添加额外的示踪标记。每次强夯后，采用ISTRA4D软件对砂土颗粒位移及地基变形情况进行PIV分析，筛选竖向位移超过 10 mm 的砂土颗粒，绘制出有效加固范围。以ID0.4试验组第6击为例，如图9所示。

图9 砂土颗粒位移分析(ID0.4，第6击)Fig.9 Displacement analysis of sand particles(ID0.4,the 6th tamping)

强夯处理后的砂土颗粒位移变化分析结果(图9)显示，红褐色区域竖向位移≤10 mm，蓝色区域竖向位移>10 mm。强夯有效加固范围沿水平方向和深度方向不断发展，按照不同的相对密实度(ID0.4、ID0.5、ID0.7)获取有效加固范围与夯击次数的关系，如图10所示。

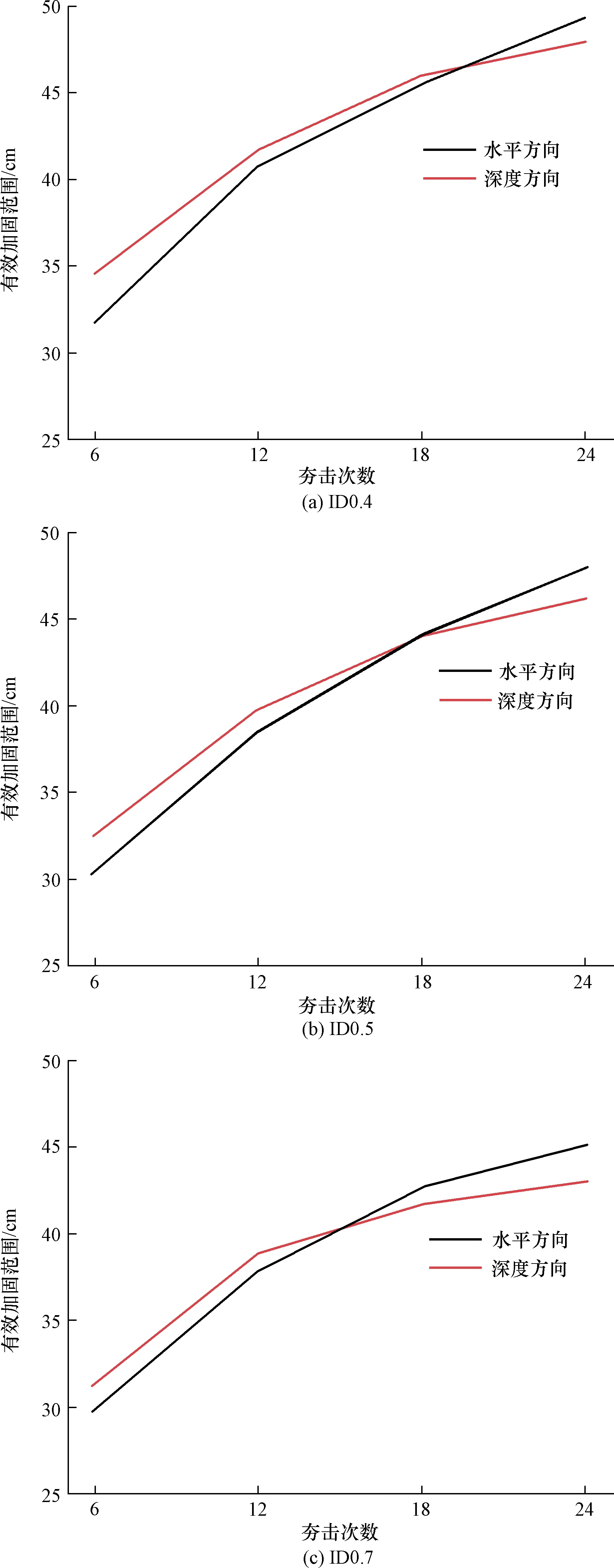
图10 有效加固范围与夯击次数的关系Fig.10 Relationship between effective reinforcement area and tamping times

由图10可知，随着夯击次数的增加，砂土地基在水平方向和深度方向的有效加固范围随之扩大。在夯击次数较少的情况下，有效加固范围在深度方向>水平方向；在夯击次数高于一定值时，有效加固范围在水平方向超过深度方向，夯锤下方的砂土地基强度达到一定值后难以继续提高，夯击能更多地向侧向土体传递，这也与砂土在夯锤冲击下产生的流动特性相关。砂土相对密实度越高，有效加固范围在水平方向超过深度方向所需的夯击次数越少；随着夯击次数的增加，深度方向有效加固范围增长放缓，ID0.4、ID0.5、ID0.7试验组分别在第20、18、15击后，水平方向有效加固范围增长大于深度方向。

3 结论

采用自行设计的模型试验装置及量测系统，结合PIV技术对3种相对密实度的德国莱比锡市赫希菲尔德地区砂土进行强夯室内模型试验，得到以下结论。

(1)第6、12、18、24击的速度时程曲线在快速下降阶段基本重合，击数越高回弹速度越高、持续时间越短，体现为能量释放时间的不同；对于ID0.4、ID0.5、ID0.7试验组，从第6击到第24击的强夯能量释放时间分别下降38.9%、34.7%、31.4%。

(2)随着夯击次数的增加，单次夯沉量逐渐减小、回弹比(回弹量/最大夯沉量)逐渐提高；ID0.4、ID0.5、ID0.7试验组在第24击的夯锤位移回弹比分别达到65.3%、67.1%、69.0%。

(3)砂土相对密实度越高，夯锤冲击力越大，夯锤加速度/动态力时程曲线在第6、12、18、24击之间的差别越小；随着夯击次数的增加，夯锤动态力峰值逐渐提高、上行曲线斜率变小，冲击行程逐渐缩短。

(4)砂土相对密实度越高，有效加固范围在水平方向超过深度方向所需的夯击次数越少；随着夯击次数的增加，深度方向有效加固范围增长放缓，ID0.4、ID0.5、ID0.7试验组分别在第20、18、15击后，水平方向有效加固范围增长大于深度方向。