一种基于属性分布的非均匀油藏数值模拟网格优化算法

史敬华， 刘钰洋， 于金彪， 强伟帆， 曹伟东， 徐睿智， 潘 懋， 张 慧

(1.长江大学地球科学学院,武汉 430100；2.中国石化胜利油田勘探开发研究院,东营 257015；3.北京大学地球与空间科学学院,北京 100871；4.北京大学造山带与构造演化教育部重点实验室,北京 100871；5.北京大学石油与天然气研究中心,北京 100871；6.中国石化胜利油田东胜公司,东营 257051)

油藏数值模拟是油气田勘探开发的基础，是指导油藏开发方案制定、调整井网部署、开发动态预测和建立合理工作制度等的重要手段[1-5]。在油田生产的整个动态过程都需要利用数模软件进行控制和监测，对数值模拟技术的研究也向着愈加精细、便捷和自动化的方向发展。

现代整体油藏模拟将数值模拟技术和精细油藏描述相结合，将精细油藏描述形成的各储层物性参数数据作为油藏数值模拟系统的原始输入数据。油藏管理的两大工具为精细地质建模和油藏数值模拟，建立的地质模型越精细越能更加准确地表达油藏储层物性和流体等各种参数的空间分布特征。精细地质模型多用细粒度的网格来表达储层的特征，网格数量一般达到数百万、数千万乃至数以亿计，如此精细的地质模型在刻画储层非均质性和流体渗流规律等方面是极其重要的。受到计算机存储量、计算速度等多方面的约束，数值模拟软件只能处理有限数量的网格数据体，网格数据量太大则不能够直接用数模软件进行计算[6-11]。虽然计算机技术发展迅猛，并行计算效率突飞猛进，但千万级或数以亿计网格数量的油藏模型计算费用高、运行速度慢，不适合广泛地用于油藏数值模拟工作[12-13]。因此，需要将精细油藏描述资料进行优化处理，经过优化处理后的地质模型在网格数量上能被现有数值模拟方法所承受，进行调整后可作为数值模拟的基础数据。将细网格中的储层物性参数科学合理地优化后赋到粗网格中去，尽量多地保留精细地质模型中储层物性非均质特征的同时，在网格数量上又能够为现有数模方法所承受，是现代油藏数值模拟技术研究的一个难点问题。

三维精细地质模型通过网格来表达储层的地质构造和物性参数的空间分布，网格数据作为油藏数值模拟系统的原始输入数据之一，是油藏数值模拟的基础，油藏网格模型质量的好坏直接影响油藏数值模拟结果的准确性[14-18]。精细油藏描述与油藏数值模拟对网格模型的要求不同，模拟模型的网格方向、网格正交性和网格的尺寸以及优化后模型的储层物性参数等都影响着油藏数值模拟的精度与效率[19-27]。

针对以上存在的问题，借鉴自适应网格法的思想，提出了一种改进的不均匀网格优化方法。该方法在储层物性非均质性强烈或重点研究区域采用细网格，而在储层物性均质性相对较好的区域采用粗网格，相邻粗、细网格间均匀渐变过渡。通过此种网格优化算法的实现，既有效保证了地质模型的准确性，又可以提高了数值模拟的效率。

首先设计了网格优化的基本原则；随后，在此基础上进行了不均匀网格优化算法的设计与实现；最后，通过X油田实例数据，验证网格优化算法的有效性和准确性。

1 网格优化基本原则

油藏数值模拟基于网格模型进行运算，网格模型数据作为数模计算的初始输入数据之一，是油藏数值模拟的基础，油藏数值模拟网格模型质量的好坏直接影响着油藏数值模拟结果的准确性，一套好的网格模型能够满足复杂油藏数值模拟的精度要求和数值模拟结果的准确性。系统的分析和梳理影响数值模拟网格的各种影响因素，主要针对数值模拟网格中的角点网格系统，基于影响该网格的各种因素，从网格方向、网格正交性和网格尺寸等方面，确定网格优化的基本控制原则，从而对后续网格优化算法的实现提供基础的质量控制和数据约束。

1.1 网格方向性优化原则

网格方向的选择是指在建立网格模型时确定采取的坐标系的方向，网格的方向对油藏属性模型、油藏数值模拟等都有很大的影响，选取网格坐标系时需要考虑油水井间的排列方式和主要断层的走向等[28]。断层的走向通常是趋于平行的，为了保持网格的正交性、减少网格的退变，需要将断层的走向或趋势线方向设置为网格某一个坐标轴的方向。当研究区呈脉状或条带状分布时，将地质模型的轴线方向设置为网格坐标系的行或列的方向可以使得建立的网格模型中网格节点数量最小化。合理的网格取向可以减少网格模型中无效网格的数量，减少断层附近网格的扭曲变形、减少网格数据占用的存储空间，更有效的表达地质构造特征(图1)。

图1 网格坐标系选择[28]Fig.1 Selection of the grid coordinate system[28]

为了减少网格取向效应的影响，在实际油田开发应用中，油藏模型网格坐标系的取向需要根据工程师和地质师的意见，结合实际地质情况和具体应用来确定。网格取向原则如下。

(1)充分考虑油水边界、断层、尖灭等天然边界，取网格坐标系的轴线方向与这些边界一致或趋于平行的方向，这样既可以减少网格的扭曲变形、保证网格间的正交性，又能够较好地表达地质构造边界形态。

(2)网格坐标系的取向考虑注采井网的排列方向，取注采方向为网格坐标系某一坐标轴的方向。

(3)考虑研究区储层展布方向，沿沉积场的轴线方向构建网格模型可以减少网格模型网格单元的数量和无效网格的数目。

1.2 网格正交性优化原则

网格的正交性影响着矩阵求解的难易程度，若网格是非正交的，那么基于正交网格推导出来的计算方程就不是严格可用的，数值模拟的结果也会产生一定的误差。

影响网格正交性的主要因素是断层的走向与分布，沿断层走向变化趋势设置控制线并将断层采用阶梯状或“Z”形处理可以较好地改善网格的正交性。首先判断研究区内断层的走向，以断层走向变化趋势方向为网格系统的横轴，即网格横轴平行于区域内主要断层的走向。然后对断层进行“Z”形处理，以断层特征点之间线段与横轴夹角为依据，将大于45°的断层线划分在纵向网格上。此外，引入拉普拉斯方程求解网格形态来保证网格的正交性。

为了避免网格正交性给数值模拟计算带来误差，设定网格正交化原则：①沿断层走向变化趋势设置控制线；②将断层采用“Z”字形处理；③引入拉普拉斯方程求解网格形态，保证网格的正交性。

1.3 网格尺寸优化原则

将精细地质模型转换为油藏数值模拟网格，需要加大精细网格模型的网格尺寸，用一系列等效的粗网格单元来替代精细网格模型中的网格单元，在网格优化的过程中容易造成信息的丢失和误差的引入。油藏数值模拟运行计算的时间与费用和优化网格的尺寸有直接的关系，优化网格采用的尺寸大小对油藏数值模拟结果的准确性也有较大的影响。网格尺寸越小越能精细刻画油藏的地质构造特征，但会增加运行计算的时间和成本；网格尺寸越大，储层非均质性和地质构造特征丢失越严重，模拟结果的可靠性越差，且会导致严重的数值弥散，影响计算精度。同时，相邻网格的尺寸不能相差太大，网格尺寸之间的差距影响着油藏数值模拟计算中形成的系数矩阵中每个元素的数值大小，各个元素之间差别太大就会形成病态的系数矩阵，从而影响数值模拟结果的准确性。当相邻网格尺寸存在较大差异时会引起压力、饱和度等流动参数的剧变，容易产生不稳定现象，在求解流动方程时带来严重的收敛问题，导致运行速度极慢、运行中断等。

借鉴自适应网格法的思想，提出了一种改进的不均匀网格优化方法。该方法在储层物性非均质性强烈或重点研究区域采用细网格，而在储层物性均质性相对较好的区域采用粗网格，相邻粗、细网格间均匀渐变过渡。

确定三维精细地质模型优化时采用网格尺寸的大小，需要综合考虑计算机的存储和运算能力、实际地质情况与优化后油藏网格的用途等因素。对网格尺寸设定了以下原则。

(1)优化后的网格模型的网格数据量能被现有油藏数值模拟方法所承受，且符合主流数值模拟器的数据处理能力。

(2)优化后的网格模型能够尽可能多地保留原始精细模型的非均质地质构造特征，减少地质信息的丢失。

(3)相邻网格间的尺寸不能相差太大，设计的网格尺寸保持均匀渐变。

(4)在近井、断层、尖灭等附近使用相对较小的网格尺寸，在远井和均质性较好处采用相对较大的网格尺寸，大网格与小网格间均匀渐变过渡。

2 网格优化算法

在精细地质模型转换为油藏数值模拟网格模型的过程中，需要对精细地质模型进行优化处理，网格优化的过程中既需要一定程度的平均化又需要尽可能多地保留精细模型中特殊地质构造特征。传统网格优化采取的优化方式为均匀优化，若网格优化尺寸较大，则储层属性特征容易丢失，数值模拟结果的可靠性变差，需要采用局部网格加密方法才可以解决上述问题；若网格优化尺寸较小，则会保留较多的网格，增加数据存储成本且影响计算机的运行速度。网格优化技术必须要解决的问题是将精细网格内的原始储层物性参数合理的优化后转换到较粗的网格上去，并使转换后的模型尽可能多地保留精细地质模型中的地质构造特征和非均质性，同时又能在网格数量上为现有油藏数值模拟方法所承受。

2.1 网格优化算法设计

借鉴自适应网格法的思想，提出了一种改进的不均匀网格优化方法。该方法在储层物性参数变化较大、非均质性强烈的区域或重点研究区域采用细网格而在储层物性参数变化较小、均质性相对较好的区域采用粗网格，相邻粗、细网格间均匀渐变过渡。不均匀优化算法构建的网格模型为一种多级网格结构(图2)，研究区域中存在有不同级次的网格，它们的空间尺度各不相同，但所有网格单元的每个侧面均只与一个网格相邻接触。所有网格级次中最基本的网格单元为初始的精细网格，网格级次用C表示，网格变化方向分别用角标I、J表示，则I方向上的网格级次为CI，最细级网格级次记为1，即(CI=1)，最粗级网格级次记为Imax即CI=Imax，网格在I方向上均匀渐变。同理，J方向上的网格级次由最细级(CJ=1)向最粗级(CJ=Jmax)渐变。各个网格单元的网格尺寸大小由组成该网格I、J方向上的网格级次决定，记第I行、第J列上的网格尺寸为S(I,J)。图2中正中心的小网格为I方向上最细级次CI=1与J方向上最细级次CJ=1组成的最细网格，四个角上的大网格为I方向上最粗级次CI=Imax与J方向上最粗级次CJ=Jmax组成的最粗网格。

不均匀网格优化方法的主要步骤如下。

(1)设置I、J方向上最大的网格级数。

(2)分别设置I、J方向上从最细级到最粗级、各级网格的空间尺度，即各级粗网格包含的细网格数目。

(3)通过计算机识别井、断层、尖灭线等所处网格的位置。

(4)设置井所处网格及其四周相邻网格所在行和列上的网格为初始最细级(网格级次为1)网格；设置主要断层和尖灭线走向上的行或列上的网格为初始最细级网格。

(5)由设置的初始最细级网格处开始，分别向四周由最细级次向最粗级次逐级优化，达到设定的最粗级次时则保持以最粗的级次进行优化。根据设定的网格级次优化研究区域的所有细网格，得到初步的优化网格模型。

(6)依次检查粗网格中所包含细网格的储层物性参数的变化大小，计算所有粗网格的变量偏差(记为Δφ)与网格细分判据(记为εφ)，进行比较。

(7)若某一行或某一列中超过1/n(n为精度校正系数，可根据油藏数值模拟的精度要求及实际应用需求而定)的粗网格的变量偏差大于设定的阈值(Δφ≥εφ)，则降低一级该行或该列粗网格的网格级次后计算变量偏差Δφ，直到Δφ<εφ，记录当前粗网格调整后的网格级次，并做标记；否则跳转到步骤(9)。

(8)从标记的粗网格处开始，根据优化规则和设定的网格级次重新调整当前优化网格模型，跳转到步骤(6)。

(9)保存优化结果，生成不均匀优化网格模型。

优化后的网格模型仍然保持原精细网格的数据组织结构，能满足油藏数值模拟的精度要求，且能较好的描述储层物性参数的非均质性，在保证计算精度的同时尽可能多地减少了网格数量。

2.2 网格映射规则设计

优化网格模型中粗细网格映射关系的设置包括水平方向上粗网格与其包含的细网格间对应关系的设置，以及垂直方向上粗网格层与其包含的细网格层间对应关系的设置。在设置网格间的映射关系时，需要避免出现网格存在“跨层”或“跨带”的情况，并根据实际地质情况，充分考虑储层地质的非均质性，设置粗、细网格模型间水平方向和垂直方向上网格序号的对应关系。

水平方向粗细网格对应关系是指根据设计的优化规则，设置各个粗网格与细网格间的包含关系。由于油藏数值模拟网格与精细地质网格所采用的网格尺寸不同，一个粗的数模网格将会包含多个精细地质细网格(图2)。

灰色线条组成的格子为初始精细网格；红色线条组成的格子为优化后的网格图 2 水平方向网格优化示意图Fig.2 Illustration of horizontal grid optimization

图2中，均匀优化即按照设定的步长，粗网格均匀的包含细网格，一般适用于地质结构简单、均质性较强的油藏。设计的不均匀优化法在储层物性参数变化较大、非均质性强烈的区域及重点研究区域采用细网格，而在储层物性参数变化较小、均质性相对较好的区域采用粗网格，相邻粗、细网格间均匀渐变过渡。不均匀优化方法能够更加精确地描述储层地质的非均质特征、能尽量多地保留原模型中丰富的地质信息，同时减少网格单元的数量，节省计算时间，提高数值模拟工作效率。

2.3 算法技术路线

不均匀优化算法的主要思路是先根据设定的网格级次对整个研究区域进行优化处理，然后通过计算所有粗网格的变量偏差Δφ，对超过1/n(n为精度校正系数，可根据油藏数值模拟的精度要求及实际应用需求而定)的粗网格的变量偏差Δφ大于网格细分判据εφ的行或列再进行局部细化调整。网格优化或局部细化的过程都是由细到粗或由粗到细逐级进行的，为了确保计算稳定，在网格优化或细化的过程中一般要求相邻网格I、J方向上网格级次之差不超过1，同时相邻网格上的网格尺寸满足式(1)：

(1)

式(1)中：Δxi表示I方向上第i级次网格的尺寸；Δxi+1表示I方向上第i+1级次的尺寸；Δyi表示J方向上第i级次网格的尺寸；Δyi+1表示J方向上第i+1级次网格的尺寸；i为某一网格级次。

在进行网格优化前，需要先设定I、J方向各网格最大级次Imax、Jmax的大小，然后根据图3中的流程图进行网格的整体优化。

Imax=1表示I方向上粗网格的尺寸等于原始精细网格模型中I方向上一个细网格的尺寸大小，即I方向上网格不优化，J方向上同理。

在井、断层、尖灭等处的液体流量及储层物性参数的变化较大，同时为了尽可能多地保留地质构造特征及储层的非均质性，将井及其四周相邻网格所在行和列上的网格以及断层和尖灭线走向上的行或列上的网格设置为初始最细级网格，即网格级次为1。根据设定的各网格级次的大小，由设置的初始最细级网格处开始，以行和列的方式向四周由最细级次向最粗级次逐级对研究区精细网格进行优化，达到设定的最粗级次时则保持以最粗的级次进行优化。当不同级次的网格相交时，先对相交网格进行整体合并，若合并后的网格尺寸大于当前网格级次的下一级网格级次的大小，则对合并的网格进行调整；否则保留合并后的网格尺寸大小。

在储层物性参数变化较大、非均质性强烈的区域或重点研究区域采用细网格，在储层物性参数变化较小、均质性较好的区域采用粗网格，研究区网格尺寸由小到大或由大到小均匀渐变过渡。根据细网格内储层物性参数的偏差来判断多孔介质内部储层物性参数的非均质性和变化大小，以此作为细分判据的控制参数。粗网格的变量偏差可通过式(2)进行计算：

Δφ=max{φi}-min{φi}

(2)

式(2)中:φi为第i级网格包含的细网格的物性参数。利用式(2)来控制粗网格内储层物性参数变化的大小，以此来决定采用的网格级次。在粗网格内，如果储层物性参数的偏差大于设定的网格细分判据(即Δφ>εφ)，则需要对此网格进行细化操作，不同相区的储层物性参数值一般相差较大，为了保证计算的精度，粗网格所包含的细网格必须位于同一相区，其细分判据的控制参数的偏差必须小于给定的阈值。对某一行/列上的网格进行细化时，先降低一级该行/列上(J/I方向)的网格级次，然后计算降级后该行/列网格储层物性参数的变化大小，逐级降级细化直到该行/列上不超过1/n(n为精度校正系数，可根据油藏数值模拟的精度要求及实际应用需求而定)的网格控制参数的偏差大于设定的网格细分判据。记录下该行/列网格经过降级后的网格级次，并由当前网格处开始，根据网格优化规则和设定的网格级次向J/I的正方向对相邻网格进行细化调整，生成调整后的优化网格模型。网格优化整体技术路线如图3所示。

图3 不均匀网格优化算法技术路线Fig.3 Technical route of non-uniform grid optimization algorithms

3 实例测试

在综合考虑各类网格的优缺点后，采用角点网格模型进行油藏数值模拟的研究，旨在建立一套能够对断层、井和储层物性的非均质特征等进行精确描述且能直接应用于主流的油藏数值模拟软件中的油藏网格模型，为解决日益复杂的油藏工程问题提供帮助。

X区位于陕西省延安地区，属黄土原地貌。区域构造位置处于向西缓倾的陕北单斜上，该单斜倾角0.5°左右。在该区未发现任何大的断层，因岩性差异在局部地区由于不均匀压实，而形成了一些鼻状隆起，幅度很小，一般不超过十米，大都不闭合。该区油层顶部埋深1 005～1 060 m，油层平均厚度12.0 m，平均孔隙度13.7%，平均渗透率2.29×10-3μm2，原始地层压力9.1 MPa，压力系数0.7～0.8，属低渗、低压、低产油藏。目前动用含油面积142.6 km2，地质储量9 000×104t。目前该区域有采油井625口，开井525口，日产液1 884 m3，日产油969 t，综合含水43.0%，动液面1 028 m，单井产能1.94 t，单井日产油水平1.85 t。累产油 465.308 1×104t，采出程度11.18%，采油速度0.85%。注水井251口，开井241口，日注水平5 744 m3，平均单井日注水24 m3，月注采比2.71，累注水1 382.623 9×104m3，累注采比1.56。该区中西部63口目前在生产加密井综合含水也高达63.9%，单井产能1.39 t/d，综合含水60.2%，动液面966 m，累计产油 37.962×104t。基于X区相关基本数据，建立起了该区域三维精细网格模型，采用本文算法，对精细网格模型进行网格优化，获得优化后的网格模型。

以该模型单层网格为例，在精细地质模型转换为油藏数值模拟网格模型的过程中，首先根据数模网格的优化原则对精细网格模型的网格方向、网格正交性等进行预处理，处理后的网格基本保持正交，能够满足现有油藏数值模拟方法的要求，随后采用网格不均匀优化算法，将精细网格模型优化为对应由细到粗、均匀过度的非均匀网格模型。网格模型不均匀优化前后的全区侧视效果对比如图4所示，全区俯视效果对比图如图5所示。将该网格模型的局部放大进行不均匀优化前后的效果对比，局部俯视效果对比如图6所示，侧视效果对比图如图7所示。

图4 网格模型不均匀优化前后对比(全区侧向视图)Fig.4 Contrast of grid model before and after non-uniform grid optimization(side view of the whole model)

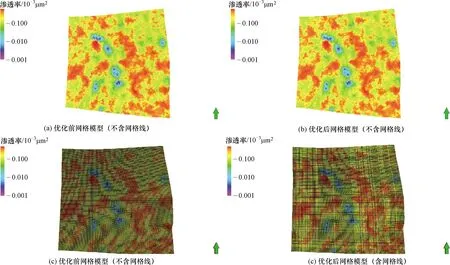
图5 网格模型不均匀优化前后对比(全区俯视图)Fig.5 Contrast of grid model before and after non-uniform grid optimization(top view of the whole model)

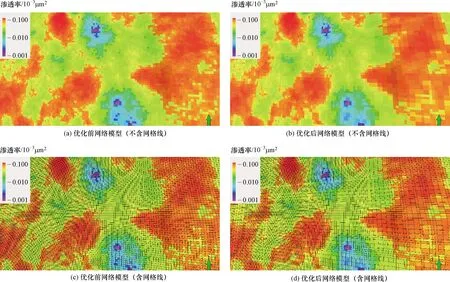
图6 网格模型不均匀优化前后对比(局部放大俯视图)Fig.6 Contrast of grid model before and after non-uniform grid optimization(top view of part model)

图7 网格模型不均匀优化前后对比(局部放大图)Fig.7 Contrast of grid model before and after non-uniform grid optimization(side view of part model)

优化前网格模型网格数量为202×202×1，优化后网格数量为170×156×1，网格数量降低了35.01%。采用属性加权分析的方式，综合分析优化前后网格属性分布(图8)，可以很明显地看出，优化前后网格属性分布基本一致，网格的属性分布特征得到了很好的保证。

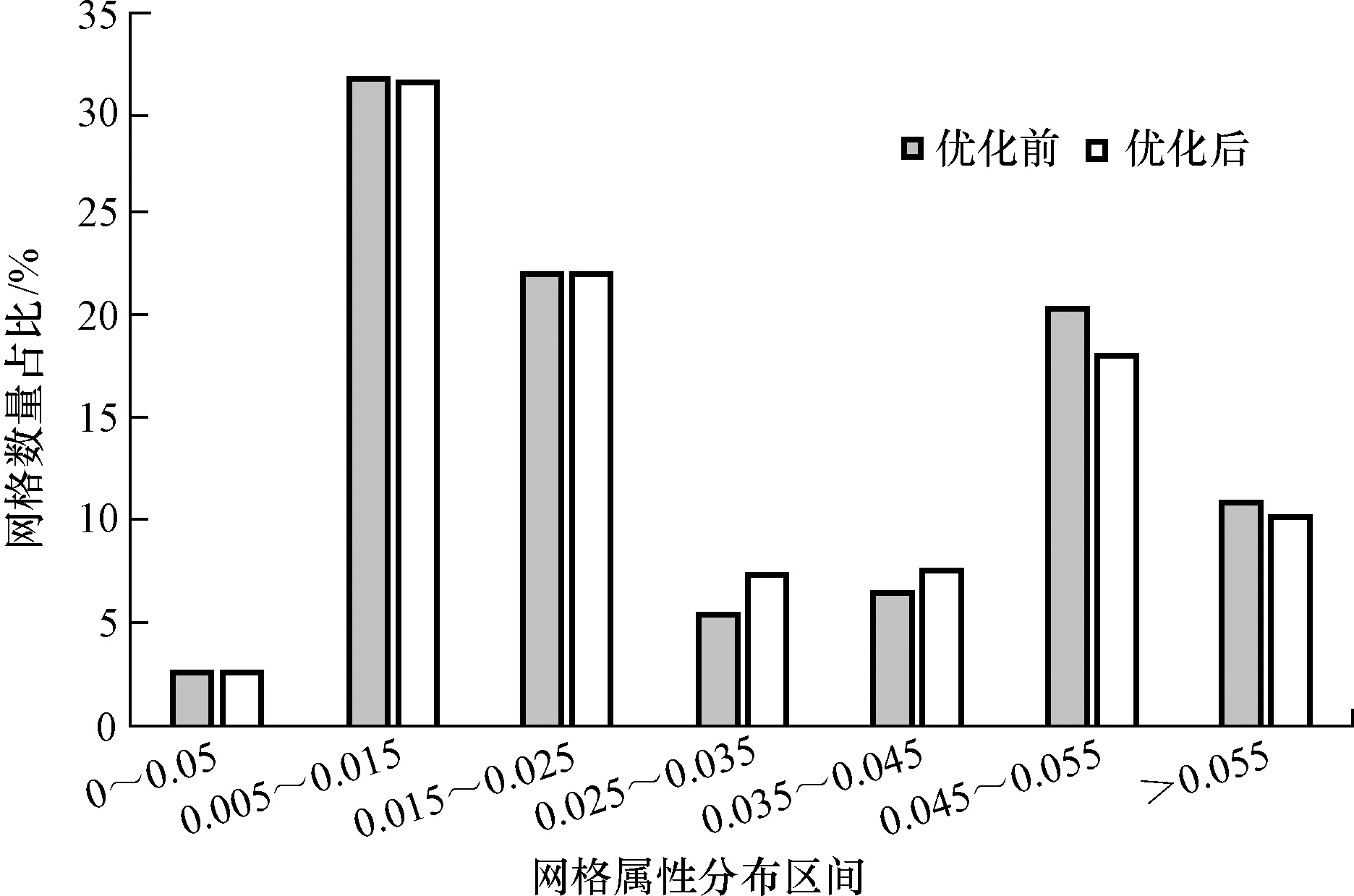
图8 网格优化前后属性分布Fig.8 Histogram of grid model attribute distribution before and after grid optimization

4 结论

通过系统分析网格优化的基本原则，在网格优化的基本原则之上设计并实现了一种非均匀网格优化算法，通过某工区实际数据对算法的有效性和准确性进行了验证，得到以下结论。

(1)通过全面地分析和梳理油藏网格模型对油藏数值模拟的影响，初步建立了一套适用于油藏数值模拟的网格模型优化原则。从油藏数值模拟网格模型的网格方向、网格正交性和网格尺寸等方面进行了系统的分析研究，在精细地质模型转换为油藏数值模拟网格模型的过程中，对网格方向、正交性等方面的处理从根本上抑制了数学模型中数值求解的不收敛因素和误差的产生。

(2)借鉴自适应网格法的思想，提出了一种多级网格结构的不均匀优化方法，该方法在储层物性非均质性强烈或重点研究区域采用细网格，而在储层物性均质性相对较好的区域采用粗网格，研究区相邻粗、细网格间均匀渐变过渡。优化后的网格模型在减少油藏网格模型网格数量的同时尽可能多地保留了储层物性参数的非均质特征。

(3)取陕西某油田某区块油藏进行了实例验证，采用提出的优化方法将精细地质模型转换为油藏数值模拟网格模型。优化后适当地减少了网格模型的网格数量，优化前后的储层物性参数概率分布具有较好的一致性，表明所建油藏数值模拟网格模型具有较高的准确度。