基于FAHP和TOPSIS法的预警机效能评估∗

（空军预警学院 武汉 430019）

1 引言

预警机将有源和无源探测设备、信息处理和通信等电子设备有机结合在一起，集预警、情报、通信和指挥等功能于一体，极大地扩展了在多威胁环境中对防御和进攻空域的监视范围，增强了其指挥控制能力，是现代作战中不可或缺的信息化武器装备［1］。开展对预警机作战效能评估的研究，对提升预警机作战效能和完善联合作战体系具有重要意义。

针对预警机效能评估问题，学术界展开了广泛的研究。文献［2］运用贝叶斯理论对预警机导航系统组成、特点和预警机使用过程分析建立综合效能评估模型；文献［3］通过建立基于任务数据的指标体系，构建BP神经网络探测效能评估模型；文献［4］在解析计算方法的基础上，根据摧毁目标值评估预警机的作战效能；文献［5］结合区间数和TOPSIS各方法的优点对预警机进行效能评估；文献［6］在加装数据链条件下，根据预警机协同敌我双方实力对比和战斗进程，在对数法的基础上，给出了预警机作战效能评估方法。模糊层次分析法具有简化分析和计算过程、综合考虑人为因素和具备思维一致性等优势，而逼近理想排序法更能反映原始数据的特性、规范了指标量纲差异问题等优点，本文将两者优势结合起来，提出一种基于模糊层次分析法和逼近理想排序法的方法来对预警机作战效能进行评估。

2 建立预警机效能评估体系

明确影响预警机作战的因素是正确有效对预警机作战效能评估的前提。因此，建立合理的预警机效能评估体系将能快速准确地评估预警机作战过程中发挥的实际作战能力。影响预警机作战效果的因素有很多，而预警机主要分为载机和任务电子系统。因而预警机效能评估指标划分为载机性能指标和任务电子系统性能指标。载机是预警机遂行作战任务的基石，载机性能主要由载荷能力、机舱容积、续航能力和飞行速度等指标构成。预警机的载荷能力越强，意味着预警机拥有更大规模的设备装置和人员编成；机舱容积关系到作战人员的工作环境的舒适度；续航时间越长意味着预警机在空中执行任务的时间越长，在有限的预警机资源条件下能发挥最大作战效能；载机飞行速度越快，意味着预警机规避威胁和威慑敌方目标的可能性提高。任务电子系统各分系统分工协作，实现预警探测、敌我识别、目标跟踪、电子干扰、情报分析等功能。任务电子系统主要由雷达分系统、电子对抗分系统、通信分系统等系统组成，因此性能指标主要有雷达探测距离、搜索方位角范围、最大引导批次、总通信道、电子对抗能力、电子干扰能力和威胁告警能力等构成。雷达探测距离代表着预警机探测敌方目标的最大范围值；预警机探测一般要求全方位搜索目标，这样才能保证对敌目标更全面的探测监视，也确保我方目标能够在不同方位被引导指挥；总通信道代表着预警机的通信传输能力，合理的资源分配为我预警机情报传送提供有力保障；电子对抗能力、电子干扰能力分别代表着预警机自卫能力、对敌方进行干扰的能力；威胁告警主要是对敌袭目标进行告警，确保我预警机的安全。综合预警机载机和任务电子系统的性能指标，则预警机作战效能评估体系结构如图1所示。

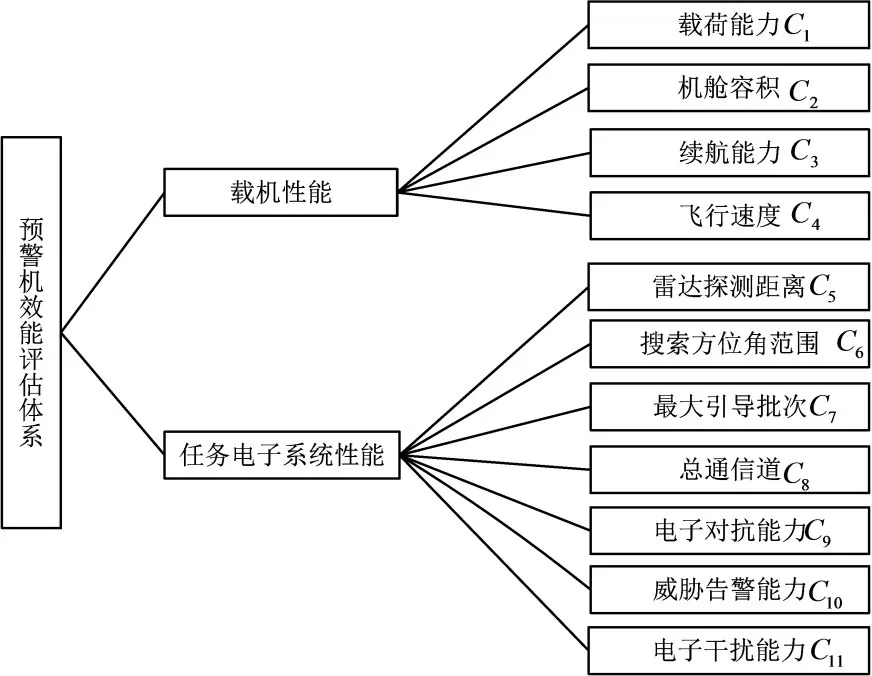
图1 预警机作战效能评估体系结构

3 基于FAHP的评估模型

模糊层次分析法（Fuzzy Analytics Hierarchy Process，FAHP）是由美国运筹学家T.L.Satty提出的一种将定性与定量相结合的系统分析方法［7］。该方法理论完备，结构严谨，能够较好解决一些非结构化、难以量化的问题。该方法具体步骤如下：

1）对单个指标进行范围分析。对预警机众多评估指标进行效能评估，要对各指标设置合理的权重并根据效能好坏进行排序，是多属性决策问题［8］。根据多属性决策方法的定义，记为评估指标集合，为方案集合，其中各评估指标相互独立，各方案也相互独立。对各指标进行范围分析，则可以得到各指标m种取值，记各取值分别为，其中为三角模糊数。则可以得到每个指标的模糊范围值为

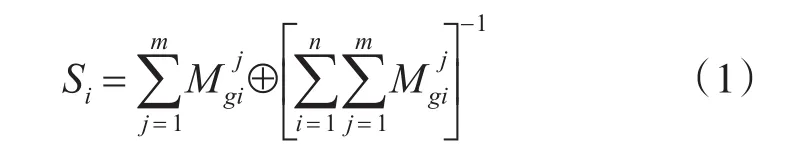
根据三角模糊数的性质［9］，则可以得到：

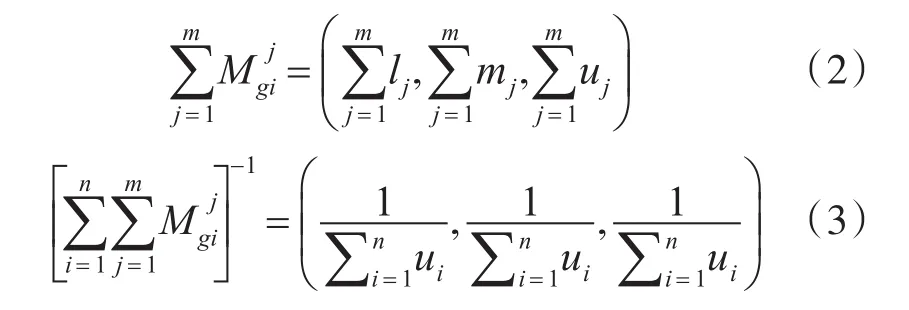
其中l，u分别表示表示三角模糊数的最低值和最高值，并满足{x∈R|l≤m≤u} 。

2）建立模糊互补判断矩阵。在模糊层次分析中，首要的是分析同一层次结构的每对指标的相对重要性，为判断任意两个评价指标对于综合评价结果的重要性，采用一个指标比另外一个指标的重要程度的定量表示。假设，为任意两个三角模糊数，则M2≥M1的可能性定义为

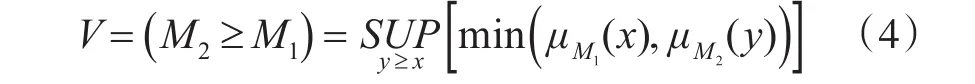
其中x，y满足l≤x≤u，l≤y≤u。并且式（2）可以等效表示为

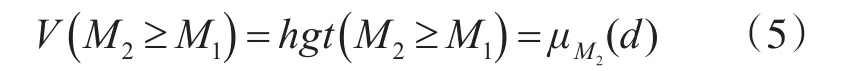
其中d为函数与函数最高交点的纵坐标 。 当m2≥m1时 ，μM2(d)=1；当l1≥u2时 ，μM2(d)=0；当在其他限制条件下，。同理也可求解。

3）指标权重的确定假设三角模糊数的数目为k，则任一模糊数M大于其他模糊数的可能性为

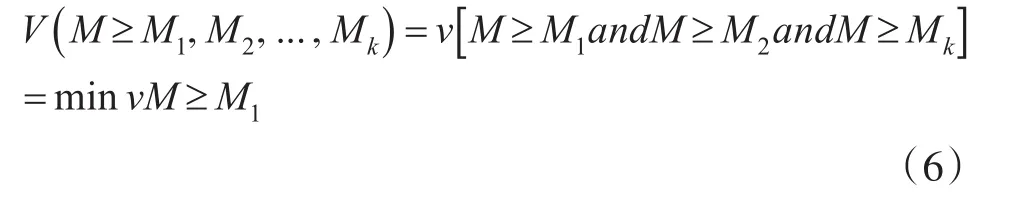
其中i=1，2，...，k。假设某一模糊数大于另外一个模糊数的可能性为d，(Ai)，则满足d，(Ai)=minV(Si≥Sk)，k∈{1 ，2，...，k} 且i≠k。则权重矩阵W为

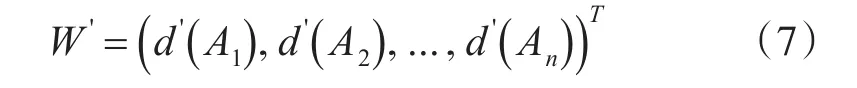
对权重矩阵归一化，则归一化权重矩阵W为

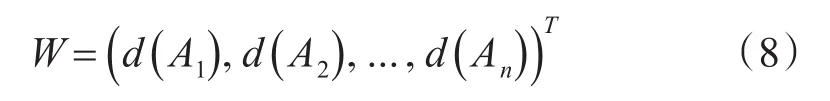
4 基于TOPSIS法进行排序

TOPSIS法是是由C.L.Hwang和K.Yoon提出，该方法将各备选方案与理想化目标最短的欧式距离的解决方案和距离负理想目标的最远欧式距离的解决方案进行对比，在两者之间得到的一个最佳的方案［10］。该方法步骤如下：

1）构造决策矩阵。假设存在m个方案，n个评价指标，专家对第i个方案在的第j个指标的评分值为rij。因为不同指标的量纲一般不相同，则归一化后的决策矩阵为。则此时决策矩阵中的项rij为

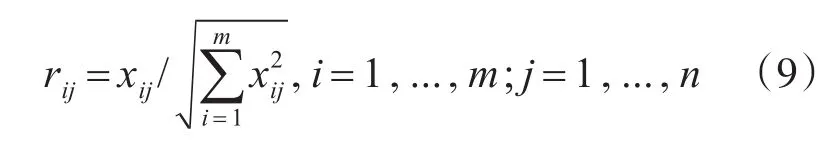
2）形成加权决策矩阵。在利用模糊层次分析法得到各评价指标的权重后，则此时决策矩阵为，加权决策矩阵的项为

3）利用加权决策矩阵获取评估目标的正负理想值。正负理想值分别为

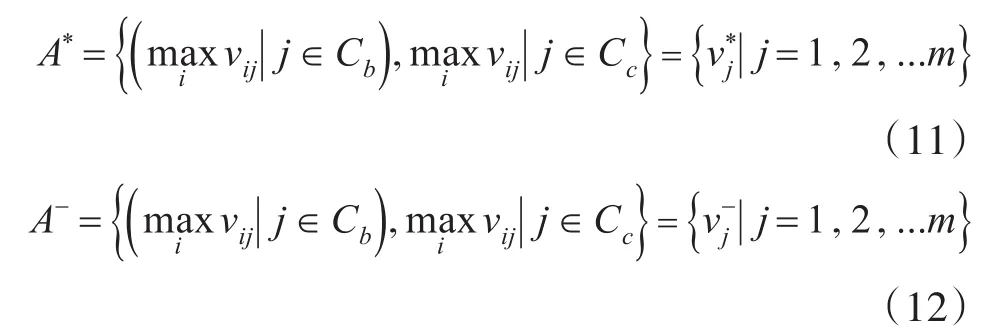
（4）计算目标值与理想值的欧式距离［11］。

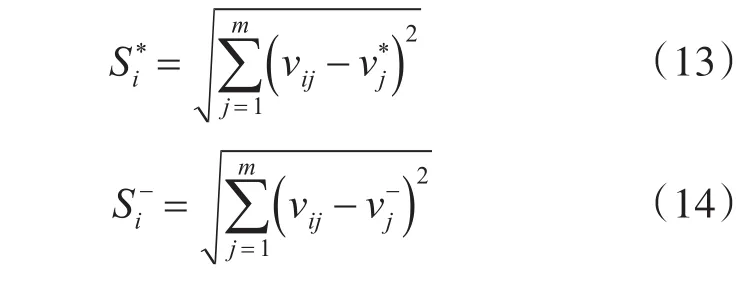
（5）计算各目标的接近程度并排序。

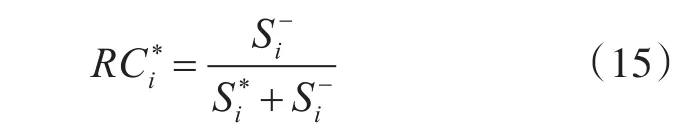
5 实例分析

在利用模糊层次分析法确定权重之前，传统方法是利用专家法来判断不同指标的重要性，判断结果原理性不强，并容易带有主观色彩。因此，在判断不同指标的重要性时利用语言变量来表示不同指标之间的重要程度［12］。如表1所示。

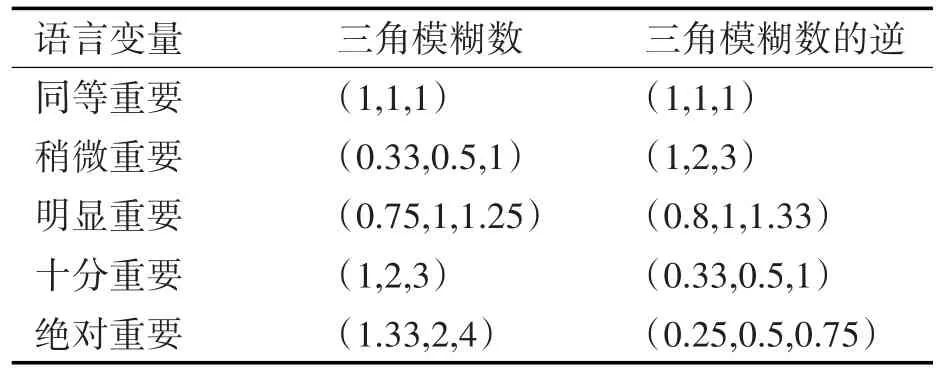
表1 语言变量及其相应的模糊数

输入预警机评估指标值C1～C11，在比较各指标之间的重要性和进行归一化处理后，记x1=(1，1，1)，x2=(0.33，0.5，1)，x3=(1，2，3)，x4=(0.75，1，1.25) ，x5=(0.8，1，1.33)，x6=(1.33，2，4)，x7=(0.25，0.5，0.75)，则各指标的模糊评估矩阵形式如表2所示。

表2 各指标的模糊评估矩阵

表3展示了行和列的总和以及各评估指标的三角模糊数范围。

指标取值范围可以利用式（1）、式（2）和式（3）进行计算，在得到各评估指标的取值范围值后计算任意一个三角模糊数大于另外一个三角模糊数的可能性，推而广之，计算大于其他三角模糊数的可能性，最后得到各评估指标的权重矩阵和归一化权重矩阵W'和W。

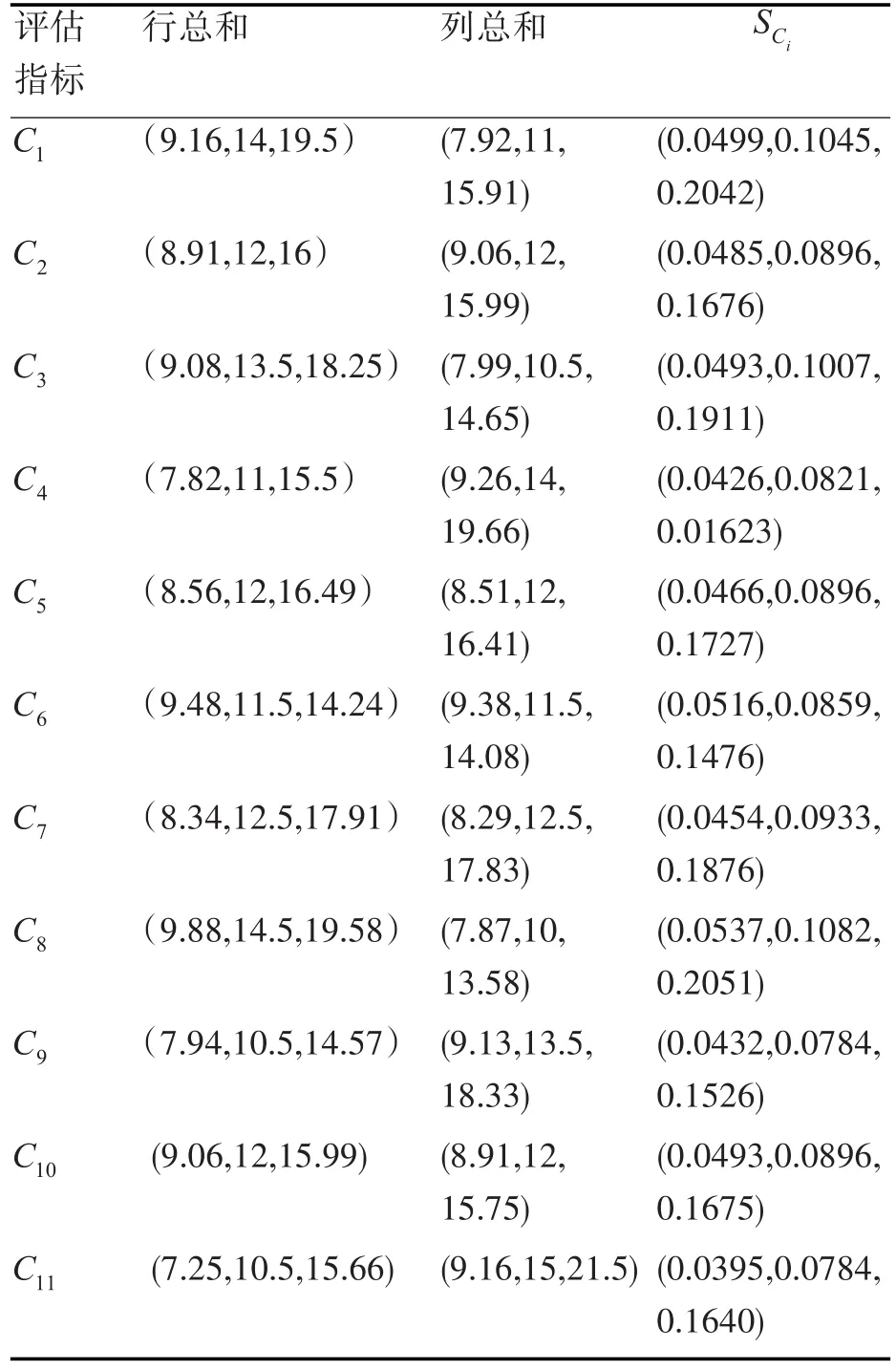
表3 模糊评估矩阵各行、各列的总和及各指标的三角模糊数范围

在使用模糊层次分析获得权重后，利用TOPSIS法计算备选方案的排名。该方法第一步是形成一个决策矩阵，并对决策矩阵进行归一化，然后将各指标权重与决策矩阵相乘，最终结果如表4。

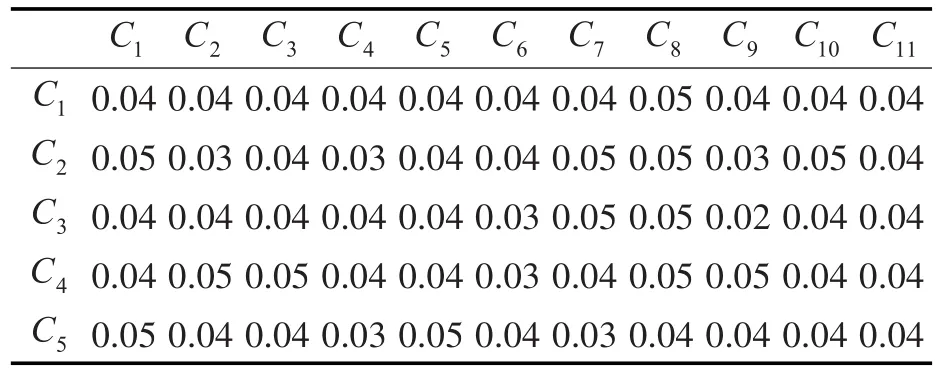
表4 各指标权重与决策矩阵相乘结果

然后通过获得每个方案的最小值和最大值，利用式（13）和式（14）得到正负理想值。

利用欧式距离方法计算各方案与正负理想方案的距离，并根据各方案的理想程度进行排序。在本文采用E-2C、E-2D、E-3F、A-50和Falcon五种预警机作为待评估的方案，在输入各预警机的性能指标后，利用模糊层次分析法和TOPSIS法进行计算，最终得到各预警机的正负理想值以及接近程度。

表5为最终的排名结果。

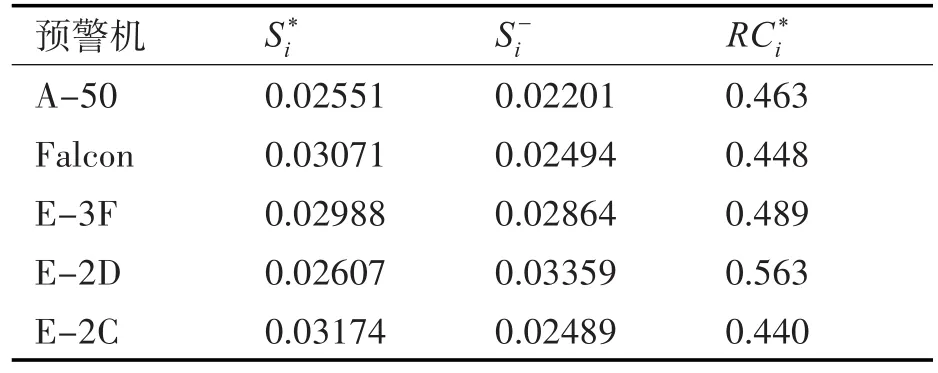
表5 五种预警机的性能评估结果

由表5可知，各预警机性能排名为E-2D＞E-3F＞ A-50＞Falcon＞E-2C，这与预警机性能实际情况较为符合。E-2D是美国研制的第三代预警机，是在E-2C的基础上改造而来，具备全新的雷达、天线、驾驶舱、显示器以及操作台等设备，具备全天候追踪以及环境觉察等功能，在总体性能上要好于传统预警机。E-3F是美国出售给法国的改进型预警机，在预警机终端显示、敌我识别、数据链和传感器等方面进行了大幅改进。A-50是前苏联在原伊尔-76运输机的基础上加装空中预警雷达，总体性能要比E-2D和E-3F差。Falcon由以色列研制生产，主要优势在于该预警机采用了先进的相控阵雷达技术。E-2C较为老旧，主要装载在航母编队上，在性能上相比其他预警机劣势较为突出。

6 结语

预警机作战效能评估指标众多，各指标间的权重难以分配，本文针对这个问题，提出了基于模糊层次分析法和逼近理想排序法的预警机效能评估方法，首先利用模糊层次分析法求解各指标间的权重，再将权重与逼近理想排序法得到的决策矩阵相乘，最后利用欧式距离来获得决策方案与正负理想方案的距离最佳的方案，并通过5种预警机实例分析，表明本方法在预警机效能评估的有效性。