萤火虫算法在鱼雷垂直命中导引方法中的仿真研究∗

（91388部队94分队 湛江 524000）

1 引言

现代海战要求为了使有限的鱼雷装药量尽可能地达到大的毁伤效果，必须尽可能地垂直命中目标。为了达到这个目的，目前国内外采用的主要方法是基于最优控制理论推导的导引方法，如文献［1］，是基于最优和次优的导引方法。国内文献［2］采用了最优控制律方法，文献［3］采用了变结构的导引方法，文献［4］采用了遗传优化的方法。在本文中，采用萤火虫算法鱼雷垂直命中导引方法进行优化，建立Simulink仿真模型，验证其可行性。

2 目标模型

参考相关文献，将鱼雷和目标运动简化为水平面运动，假定其为质点模型。相对运动关系如图1所示。相对运动方程为

式中：

at为鱼雷的法向指令加速度；am为目标的法向指令加速度；vt，vm为分别为鱼雷和目标的速度；r为目标和鱼雷之间的距离；ψt，ψm为分别为鱼雷的偏航角和目标的航向角；q为视线角。

起始时刻目标和鱼雷的运动关系为

终端约束条件为

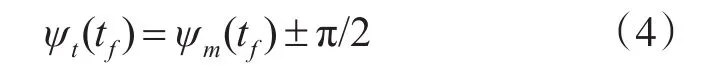
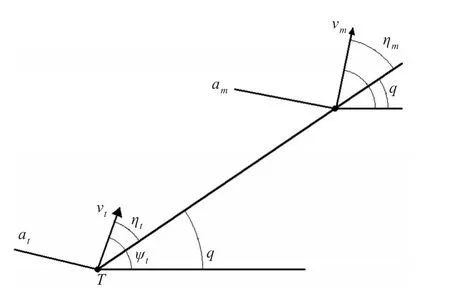
图1 鱼雷与目标的相对运动关系

参考文献［5］，取拦截时间和能量的组合作为性能指标，即：

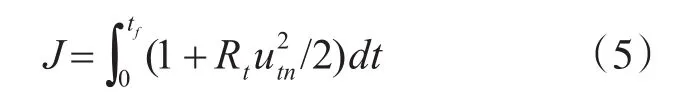
控制的目的是寻找合适的控制律utn，在满足式（4）的情况下，保证式（5）最小。参考文献［6］，可知控制律utn是r、q和ψt的非线性函数，故选取非线性控制律为

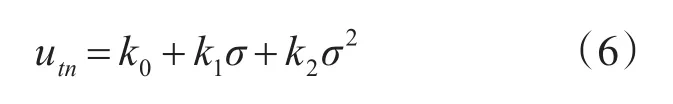
式中：

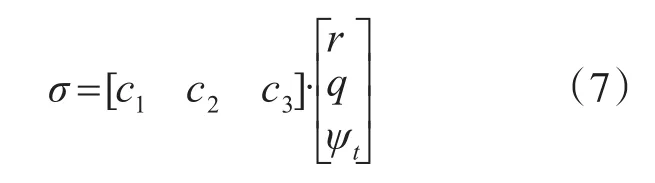
这样就将最优垂直命中问题转化为了参数优化求取式（5）的极小值问题。也就为应用萤火虫方法优化导引方法推导好了数学模型。

3 萤火虫算法

萤火虫算法（GSO）是由印度学者Krishnan和Ghose提出的一种群智能随机优化算法［7～8］。该算法模拟自然界中的萤火虫过荧光素值大小相互吸引对方，达到彼此交流信息的目的方法。相关资料表明，萤火虫算法在寻找各种全局最优解方面比遗传算法等更有效，成功率更高［9～10］。

萤火虫算法的具体算法步骤如图2描述［11～12］。

4 萤火虫算法优化垂直命中导引方法设计仿真

根据上文分析，本文所研究内容主要有7个参数 (c1，c2，c3，k1，k2，k3，tf)需要优化，本文采用萤火虫算法来优化导引命中律参数，主要方法是在每个采样周期上对所述需整定的参数进行设置和调整，以找到最优的控制参数。其主要原理可以描述为首先将每个萤火虫个体对应一组导引律参数，然后在每次算法迭代中计算每个萤火虫个体的控制量，并计算出相应的系统输出和评价函数的适应度值。并且根据萤火虫个体所处位置的优劣选取此次迭代的最优的萤火虫个体，最后将得到的最优萤火虫个体所处的位置参数作为最后的导引律控制参数。系统如图3所示。

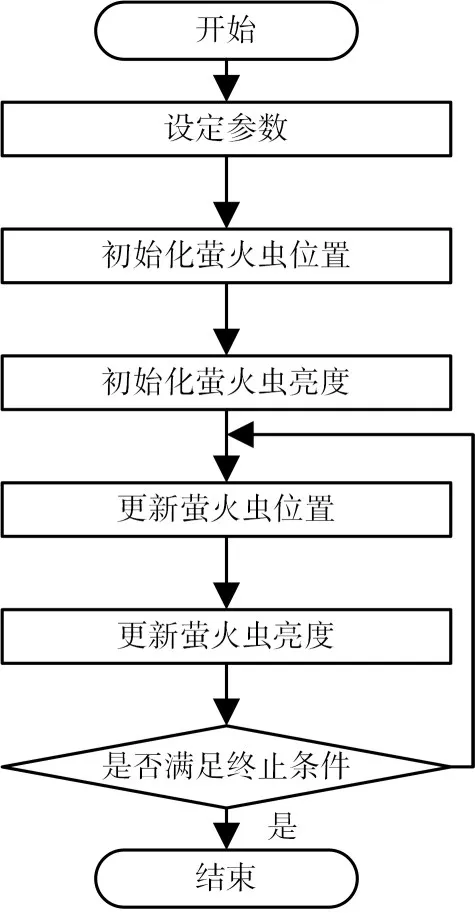
图2 萤火虫算法流程图

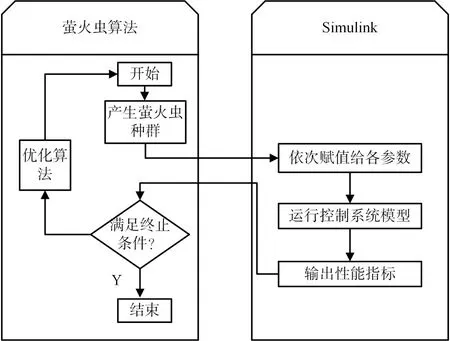
图3 萤火虫算法优化导引方法参数过程示意图

在本文中，萤火虫算法采用实数编码。假定萤火虫种群规模为N。需要优化的参数有7个，则问题域的维数为7。因此优化导引律参数的萤火虫种群可用一个N*7的矩阵表示。

目标函数F：

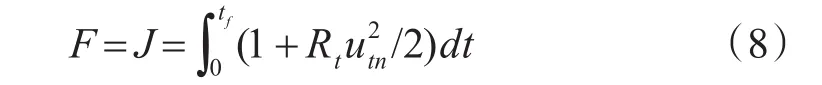
设定采样周期为0.02s，目标速度15m/s，鱼雷速度20m/s，初始时刻视线角q为60°，初始距离500m。在Matlab中建立的优化模型如图4所示。

图4 优化仿真模型

仿真结果如图5、6所示。

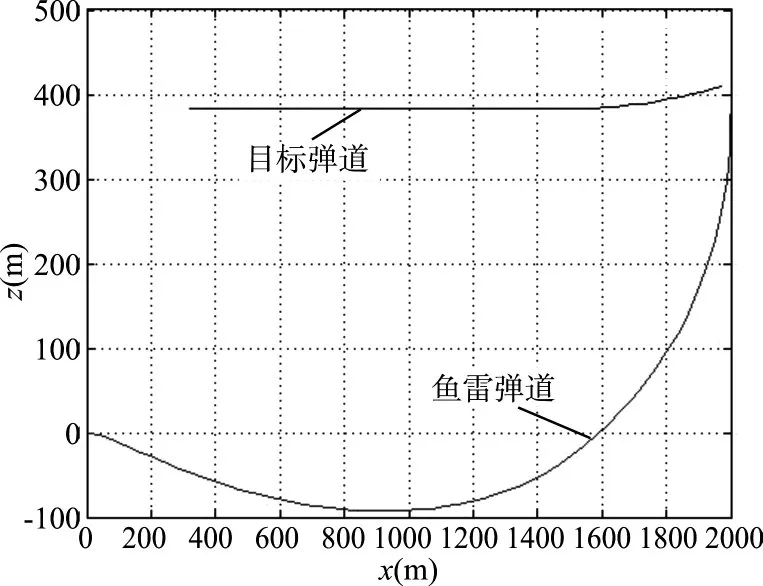
图5 目标与鱼雷的导引弹道

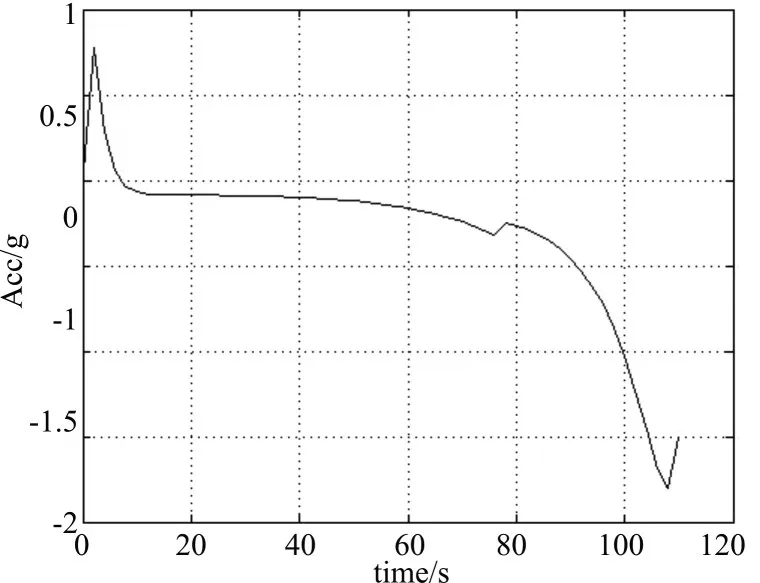
图6 鱼雷加速度

结果：脱靶量为0.707，交会角为89.4096，拦截时间为111.78。

由仿真结果可以看出鱼雷导引弹道比较光滑，命中角度接近垂直，仿真结果说明采用萤火虫算法优化鱼雷垂直命中导引方法是确实可行的。

5 结语

本文基于传统的垂直命中导引优化方法设计困难的问题，设计了萤火虫优化算法，利用Matlab构建了仿真模型。仿真结果表明，鱼雷导引弹道比较光滑，命中角度接近垂直，跟踪过程较平稳，响应速度快，鲁棒性强。可以说采用萤火虫算法优化鱼雷垂直命中导引方法是确实可行的。